算法练习-A+B/财务管理/实现四舍五入/牛牛的菱形字符(题目链接+题解打卡)
难度参考
难度:简单
分类:熟悉OJ与IDE的操作
难度与分类由我所参与的培训课程提供,但需要注意的是,难度与分类仅供参考。以下内容均为个人笔记,旨在督促自己认真学习。
题目
| A + B | 1. A + B - AcWing题库 |
| 财务管理 | 1004:财务管理 |
| 实现四舍五入 | 实现四舍五入 |
| 牛牛的字符菱形 | 牛牛的字符菱形 |
题解
A+B

#include <iostream>
#include <cstdio>using namespace std;int a,b;
int main(){cin>>a>>b;cout<<a+b<<endl;return 0;
}时间复杂度为O(1)。
空间复杂度也是O(1)。
本题据说还有十几种其他恶搞版题解,待学成之后仔细研究一下。
财务管理
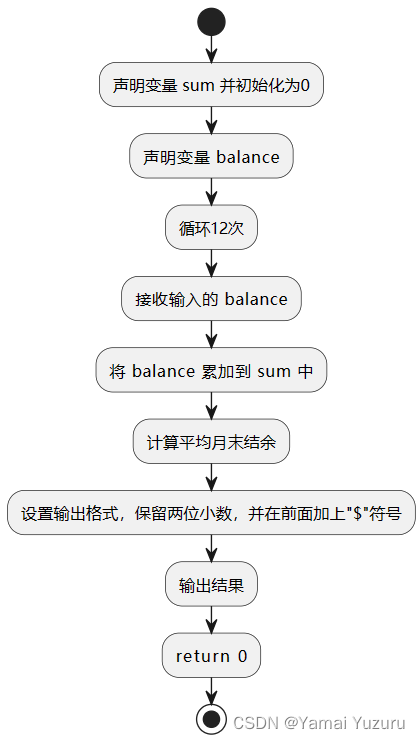
#include <iostream>
#include <iomanip> // 用于设置输出格式using namespace std;int main() {double sum = 0.0; // 初始化总结余为0double balance; // 用于存储每个月的结余for (int i = 0; i < 12; i++) {cin >> balance; // 输入每个月的结余sum += balance; // 累加到总结余中}double average = sum / 12.0; // 计算平均月末结余// 设置输出格式,保留两位小数,并在前面加上"$"符号cout << fixed << setprecision(2) << "$" << average << endl;return 0;
}时间复杂度为O(1)。(循环次数固定)
空间复杂度也是O(1)。
使用iomanip库,可以直接用fixed去保留小数个数。
实现四舍五入
使用cmath库的话,里面有直接的四舍五入的函数。
#include <iostream>
#include <cmath>
using namespace std;int main() {double floatingNumber;cin >> floatingNumber;// 将浮点数四舍五入并转换为整数int roundedNumber = round(floatingNumber);cout << roundedNumber << endl;return 0;
}时间复杂度为O(1)。
空间复杂度也是O(1)。
不过常见的做法是利用加减0.5后强制转化后实现四舍五入。加减的原因是正数为加,负数为减。
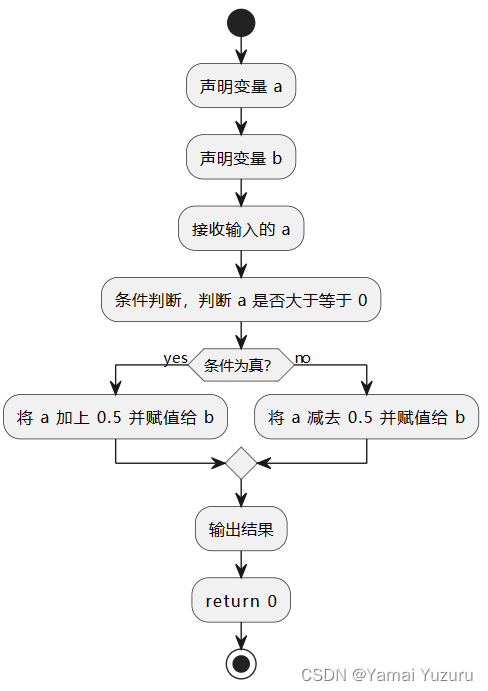
#include <iostream>
using namespace std;int main() {float a;int b;cin >> a;// 判断浮点数的小数部分是否大于等于0.5if (a >= 0) {b = a + 0.5;} else {b = a - 0.5;}cout << b << endl;return 0;
}时间复杂度为O(1)。
空间复杂度也是O(1)。
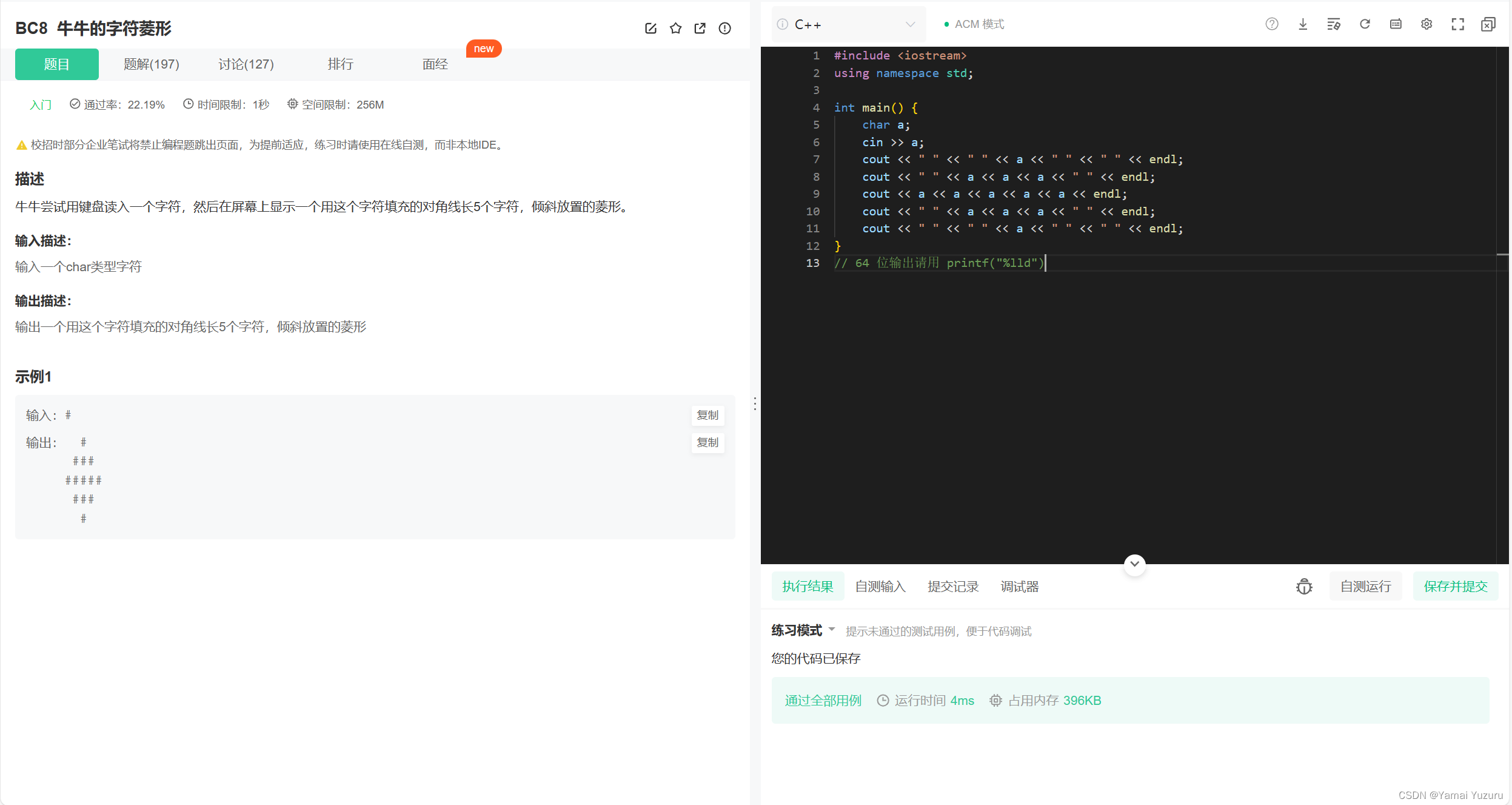
牛牛的字符菱形
明显的懒鬼做法。
#include <iostream>
using namespace std;int main() {char a;cin >> a;cout << " " << " " << a << " " << " " << endl;cout << " " << a << a << a << " " << endl;cout << a << a << a << a << a << endl;cout << " " << a << a << a << " " << endl;cout << " " << " " << a << " " << " " << endl;
}
时间复杂度为O(1)。
空间复杂度也是O(1)。
动点脑子。
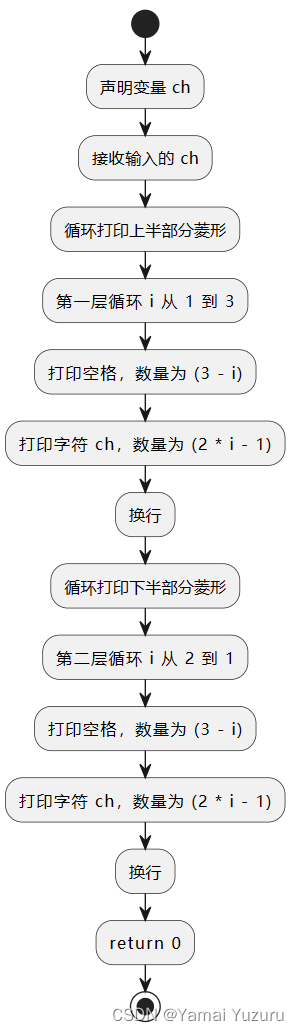
#include <iostream>
using namespace std;int main() {char ch;cin >> ch;// 上半部分菱形for (int i = 1; i <= 3; i++) {for (int j = 1; j <= 3 - i; j++) {cout << " ";}for (int j = 1; j <= 2 * i - 1; j++) {cout << ch;}cout << endl;}// 下半部分菱形for (int i = 2; i >= 1; i--) {for (int j = 1; j <= 3 - i; j++) {cout << " ";}for (int j = 1; j <= 2 * i - 1; j++) {cout << ch;}cout << endl;}return 0;
}思路
-
首先,我们从用户那里接收一个字符作为输入,并将其存储在变量
ch中。 -
然后,我们使用两个循环来打印菱形图案。上半部分的循环用于打印每一行的空格和字符,下半部分的循环用于打印下半部分的空格和字符。
-
对于上半部分的循环,我们使用一个外层循环来迭代打印每一行。循环变量
i的范围是从1到3,即打印3行。每一行前面的空格的数量是3 - i,通过内层循环来输出。 -
内层循环使用变量
j从1递增到(2 * i - 1)来打印每一行的字符(ch)。这是因为每一行的字符数量符合等差数列的规律,首项是 1,公差是 2。 -
上半部分的循环结束后,我们开始打印下半部分的菱形图案。这里我们使用一个外层循环来迭代打印每一行。循环变量
i的范围是从2到1,即打印2行。每一行前面的空格的数量是3 - i,通过内层循环来输出。 -
内层循环同样使用变量
j从1递增到(2 * i - 1)来打印每一行的字符(ch)。 -
最后,我们通过输出换行符来确保每一行之后都换行。
打卡
A+B
财务管理

实现四舍五入

牛牛的字符菱形
相关文章:

算法练习-A+B/财务管理/实现四舍五入/牛牛的菱形字符(题目链接+题解打卡)
难度参考 难度:简单 分类:熟悉OJ与IDE的操作 难度与分类由我所参与的培训课程提供,但需要注意的是,难度与分类仅供参考。以下内容均为个人笔记,旨在督促自己认真学习。 题目 A B1. A B - AcWing题库财务管理1004:财…...

XSS语句
XSS测试语句 在测试网站是否存在XSS漏洞时,应该输入一些标签如<,>输入后查看网页源代码是否过滤标签,如果没过滤,很大可能存在XSS漏洞。 <h5>1</h5> <span>1</span> <SCRIPT>alert(document.cookie)&l…...
AD导出BOM表 导出PDF
1.Simple BOM: 这种模式下,最好在pcb界面,这样的导出的文件名字是工程名字,要是在原理图界面导出,会以原理图的名字命名表格。 直接在菜单栏 报告->Simple BOM 即可导出物料清单,默认导出 comment pattern qu…...

linux 的nobody是什么用户? 对安全有没有影响?
目 录 一、前言:nobody是不是可疑用户? 二、Linux系统中的nobody用户? 二、有nobody用户存在,安全吗? 一、前言:nobody是不是可疑用户? 在前面一篇文章“Linux安全问题,如何查看哪…...

2024年华数杯国际数学建模B 光伏电(Problem B: Photovoltaic Power)完整思路以及源代码分享
背景 中国的电力构成包括传统的能源发电(如煤炭、石油和天然气)、可再生能源发电 (如水力发电、风能、太阳能和核能)和其他形式的电力。这些发电方式在满足中 国巨大的电力需求方面发挥着至关重要的作用。根据最新数据…...

在 Spring MVC 中,用于接收前端传递的参数的注解有以下几种
目录 RequestParam: PathVariable: RequestBody: RequestHeader: CookieValue: RequestParam: 用于获取请求参数的值。可以指定参数名称和默认值。示例代码: GetMapping("/users&q…...

K8s常用命令
查看集群各节点的状态 部署应用 删除一个service服务 查询service服务列表 kubectl get services 查看网络资源 kubectl get svc pod 创建一个namespace kubectl create namaspace namespace名称 创建一个pod 通常不需要创建pod 查看pod kubectl get pods kube…...

MySQL的基本操作
目录 序言 一、SQL语句(Structured Query Language) 1.1 SQL简介 1.2 SQL语句的分类 1.3 SQL语句的书写规范 二、数据库操作 2.1 查看库 2.2 创建库 2.3 切换库 2.4 删除库 三、MySQL字符集 3.1 MySQL字符集的分类 3.2 UTF8和UTF8MB4的区别…...
【b站咸虾米】chapter4_vue组件_新课uniapp零基础入门到项目打包(微信小程序/H5/vue/安卓apk)全掌握
课程地址:【新课uniapp零基础入门到项目打包(微信小程序/H5/vue/安卓apk)全掌握】 https://www.bilibili.com/video/BV1mT411K7nW/?p12&share_sourcecopy_web&vd_sourceb1cb921b73fe3808550eaf2224d1c155 四、vue组件 uni-app官网 …...
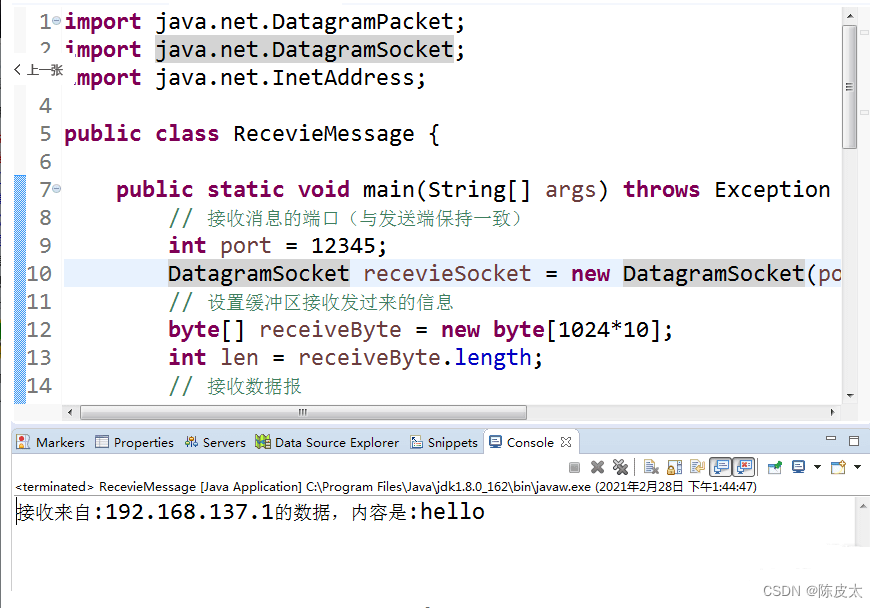
Java网络编程——UDP通信原理
一、TCP和UDP概述 传输层通常以TCP和UDP协议来控制端点与端点的通信 TCPUDP协议名称传输控制协议用户数据包协议是否连接面向连接的协议。数据必须要建立连接无连接的协议,每个数据报中都给出完整的地址信息,因此不需要事先建立发送方和接受方的连接是…...

Spring | Srping AOP (AOP简介、动态代理、基于“代理类”的AOP实现)
目录: 1.Spring AOP简介1.1 AOP简介1.2 AOP术语 2.动态代理2.1 JDK动态代理2.2 CGLIB代理 3.基于“代理类”的AOP实现3.1 Spring的通知类型3.2 ProxyFactoryBean ( 可通知.xml配置文件完成aop功能 ) 1.Spring AOP简介 1.1 AOP简介 Spring的AOP模块,是Spring框架体系…...

StarRocks 生成列:百倍提速半结构化数据分析
半结构化分析主要是指对 MAP,STRUCT,JSON,ARRAY 等复杂数据类型的查询分析。这些数据类型表达能力强,因此被广泛应用到 OLAP 分析的各种场景中,但由于其实现的复杂性,对这些复杂类型分析将会比一般简单类型…...

数据结构---数组
一、基本概念 1. 存放一组相同数据类型的集合 2.在内存中,分配连续的空间,数组创建时要指定大小 3. 定义 数据类型 [] 数组名 // 1.定义一个数组,里面的元素包含10, 20, 24, 17, 35, 58, 45, 74 int arr[] {10, 20, 24, 17, 35, 58, 45, 74}; 4. 获取数组的长度 int lengt…...
———链式语句中fetchSql和force和bind用法)
知识笔记(八十四)———链式语句中fetchSql和force和bind用法
fetchSql: fetchSql用于直接返回SQL而不是执行查询,适用于任何的CURD操作方法。 例如: $result Db::table(think_user)->fetchSql(true)->find(1);输出result结果为: SELECT * FROM think_user where id 1 force&#…...

为什么要用B+树
B树的优势 支持范围查询:B树在进行范围查询时,只需要从根节点一直遍历到叶子节点,因为数据都存储在叶子节点上,而且叶子节点之间有指针连接,可以很方便的进行范围查询 支持排序:B树的叶子节点按照关键字顺…...

Android 通过adb命令查看应用流量
一. 获取应用pid号 通过adb shell ps -A | grep 包名 来获取app的 pid号 二. 查看应用流量情况 使用adb shell cat /proc/#pid#/net/dev 命令 来获取流量数据 备注: Recevice: 表示收包 Transmit: 表示发包 bytes: 表示收发的字节数 packets: 表示收发正确的…...

超全的测试类型详解,再也不怕面试答不出来了!
在软件测试工作过程中或者在面试过程中经常会被问到一些看起来简单但是总是有些回答不上的问题,比如你说说“黑盒测试和白盒测试的区别?”,“你们公司做灰度测试么?", ”α测试和β测试有什么不一样?“࿰…...
【Linux】
Linux零基础入门 列出文件/文件夹新建/切换路径查看当前路径重命名或者移动文件夹拷贝文件/文件夹删除文件夹设置环境变量编辑文本文件压缩和解压查看cpu的信息查看/杀死进程查看进程的CPU和内存占用重定向日志场景一场景二场景三场景四 列出文件/文件夹 命令:Ls(L…...
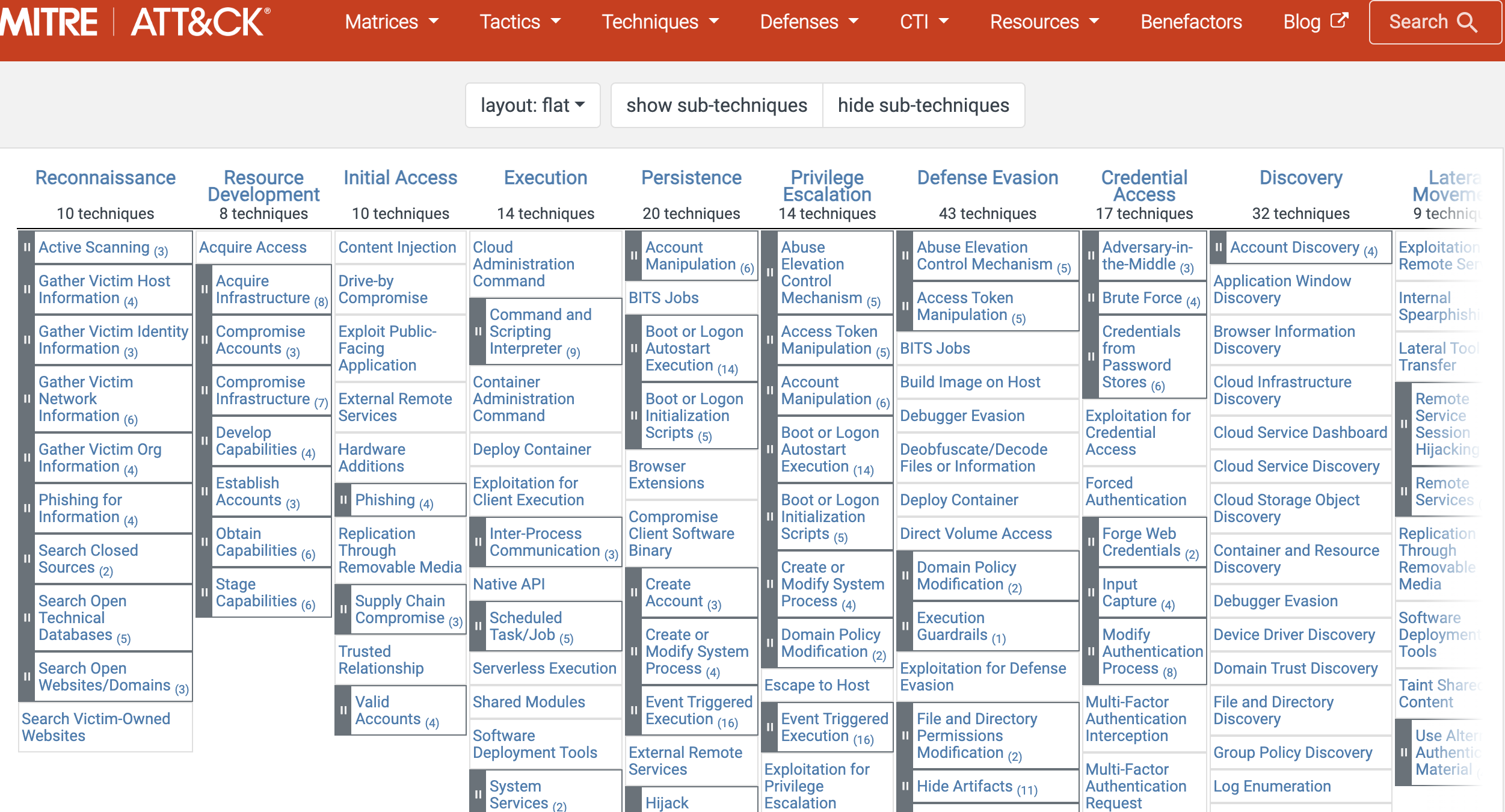
「 网络安全常用术语解读 」网络攻击者的战术、技术和常识知识库ATTCK详解
引言:随着网络攻击手段的不断升级和多样化,网络安全领域面临着越来越严峻的挑战。为了帮助网络安全专业人员更好地识别和防御网络攻击,MITRE公司创建了ATT&CK框架,以提供一个统一且结构化的方法来描述网络攻击者的行为和技巧。…...

Java.lang.Integer类详解
Java.lang.Integer类详解 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在今天的文章中,我们将深度解析Java中的一个重要类——java.lang.Integer&…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...

宠物车载安全座椅市场报告:解读行业趋势与投资前景
一、什么是宠物车载安全座椅? 宠物车载安全座椅是一种专为宠物设计的车内固定装置,旨在保障宠物在乘车过程中的安全性与舒适性。它通常由高强度材料制成,具备良好的缓冲性能,并可通过安全带或ISOFIX接口固定于车内。 近年来&…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...
