为什么要用B+树
B+树的优势
支持范围查询:B+树在进行范围查询时,只需要从根节点一直遍历到叶子节点,因为数据都存储在叶子节点上,而且叶子节点之间有指针连接,可以很方便的进行范围查询
支持排序:B+树的叶子节点按照关键字顺序存储,可以快速支持排序操作,提供排序效率
存储更多的索引数据:因为它的非叶子节点只能存储索引关键字,不存储实际数据,因此可以存储更多的索引数据
在节点分裂和合并时,IO操作少:B+树的叶子节点的大小是固定的,而且节点的大小一般都会设置为一页的大小,这就使得节点分裂和合并时,IO操作很少,只需读取和写入一页
有利于磁盘预读:由于B+树的节点大小是固定的,因此可以很好的利用磁盘预读特性,一次行读取多个节点到内存中,可以减少IO操作次数,提高查询效率
有利于缓存:B+树的非叶子结点只存储执行子节点的指针,二步存储数据,这样可以使得缓存能搞容纳更多的索引数据,从而提供缓存的命中率,加快查询速度
为什么不使用B数和红黑树
B+树只有叶子节点存储数据,而非叶子节点不存储数据,可以存储更多的索引数据
节点大小固定,可以存储更多的索引数据
叶子节点之间是双向链表链接的,可以很方便的进行范围查询
叶子节点按照关键子顺序存储,更好的支持排序
所以,使用B+树实现索引有很多好处,比如我们前面提到的支持范围查询、有利于磁盘预读、有利于优化排序等等。而这些是红黑树和B树做不到的
相关文章:

为什么要用B+树
B树的优势 支持范围查询:B树在进行范围查询时,只需要从根节点一直遍历到叶子节点,因为数据都存储在叶子节点上,而且叶子节点之间有指针连接,可以很方便的进行范围查询 支持排序:B树的叶子节点按照关键字顺…...

Android 通过adb命令查看应用流量
一. 获取应用pid号 通过adb shell ps -A | grep 包名 来获取app的 pid号 二. 查看应用流量情况 使用adb shell cat /proc/#pid#/net/dev 命令 来获取流量数据 备注: Recevice: 表示收包 Transmit: 表示发包 bytes: 表示收发的字节数 packets: 表示收发正确的…...

超全的测试类型详解,再也不怕面试答不出来了!
在软件测试工作过程中或者在面试过程中经常会被问到一些看起来简单但是总是有些回答不上的问题,比如你说说“黑盒测试和白盒测试的区别?”,“你们公司做灰度测试么?", ”α测试和β测试有什么不一样?“࿰…...
【Linux】
Linux零基础入门 列出文件/文件夹新建/切换路径查看当前路径重命名或者移动文件夹拷贝文件/文件夹删除文件夹设置环境变量编辑文本文件压缩和解压查看cpu的信息查看/杀死进程查看进程的CPU和内存占用重定向日志场景一场景二场景三场景四 列出文件/文件夹 命令:Ls(L…...
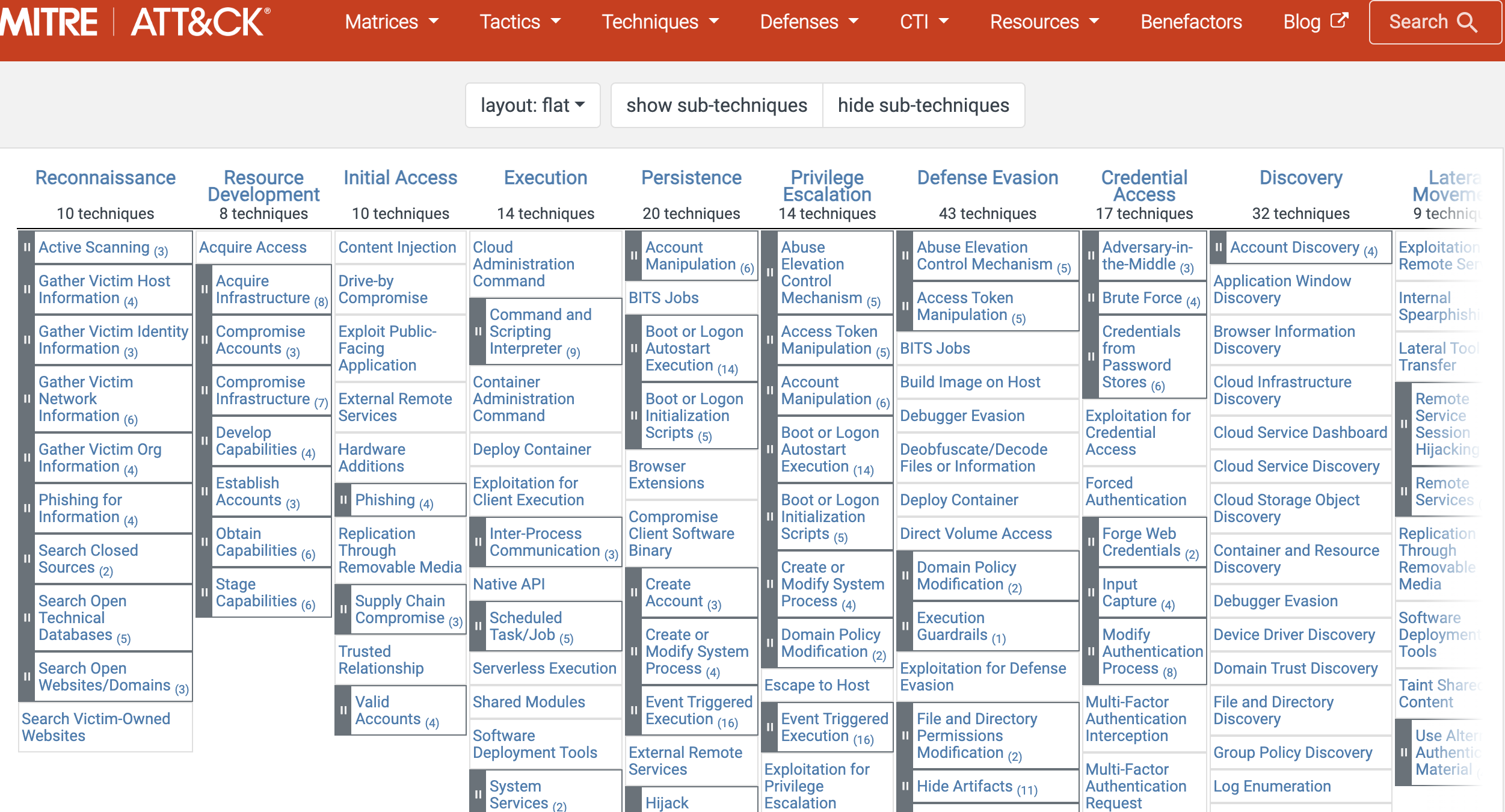
「 网络安全常用术语解读 」网络攻击者的战术、技术和常识知识库ATTCK详解
引言:随着网络攻击手段的不断升级和多样化,网络安全领域面临着越来越严峻的挑战。为了帮助网络安全专业人员更好地识别和防御网络攻击,MITRE公司创建了ATT&CK框架,以提供一个统一且结构化的方法来描述网络攻击者的行为和技巧。…...

Java.lang.Integer类详解
Java.lang.Integer类详解 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在今天的文章中,我们将深度解析Java中的一个重要类——java.lang.Integer&…...

GitFlow工作流
基于 Git 这一版本控制系统,通过定义不同的分支,探索合适的工作流程来完成开发、测试、修改等方面的需求。 例如:在开发阶段,创建 feature 分支,完成需求后,将此分支合并到 develop 分支上;在发…...

GitHub Copilot 与 OpenAI ChatGPT 的区别及应用领域比较
GitHub Copilot 和 OpenAI ChatGPT 都是近年来颇受关注的人工智能项目,它们在不同领域中的应用继续引发热议。本文旨在分析和比较这两个项目的区别,从技术原理、应用场景、能力和限制、输出结果、能力与限制和发展前景等方面进行综合评估,帮助…...

【C++】类和对象(上篇)
文章目录 🛟一、面向过程和面向对象初步认识🛟二、类的引入🛟三、类的定义📝1、类的两种定义方式📝2、成员变量命名规则的建议 🛟四、类的访问限定符及封装🍩1、访问限定符🍩2、封装…...

甜蜜而简洁——深入了解Pytest插件pytest-sugar
在日常的软件开发中,测试是确保代码质量的关键步骤之一。然而,对于测试报告的生成和测试结果的可读性,一直以来都是开发者关注的焦点。Pytest插件 pytest-sugar 以其清晰而美观的输出,为我们提供了一种愉悦的测试体验。本文将深入介绍 pytest-sugar 插件的基本用法和实际案…...

SpringBoot3整合OpenAPI3(Swagger3)
文章目录 一、引入依赖二、使用1. OpenAPIDefinition Info2. Tag3. Operation4. Parameter5. Schema6. ApiResponse swagger2更新到3后,再使用方法上发生了很大的变化,名称也变为OpenAPI3。 官方文档 一、引入依赖 <dependency><groupId>…...

2023美赛各题分析,2024美赛数学建模思路解析2.2日第一时间更新
目录 2024美赛数学建模各题思路模型代码:开赛后第一时间更新,更新见文末 一、2023题目重述 拟解决的问题 我们的工作: 二、模型和计算 1.数据预处理 2.报告数量区间预测模型 3.猜词结果分布预测模型 2024美赛数学建模交流࿰…...
分享一个学习git的网站
Learn Git Branching...

用户拉新的4大关键策略,照着做就对了!
今天给大家分享用户拉新的4个关键策略,掌握了这些策略,不仅有助于增加用户数量,还能让对方成为你忠实的粉丝。 1、制定明确的目标:在开始拉新之前,你需要明确自己的目标。你想要吸引什么样的用户?你希望他…...
如何用“VMware安装Ubuntu”win11系统?
一、 下载Ubuntu 企业开源和 Linux |Ubuntu的 二、 安装 三、 启动虚拟机 选中Try or Install Ubuntu Server,按回车...

ZJOI2009 对称的正方形
P2601 [ZJOI2009] 对称的正方形 题目大意 给定一个 n m n\times m nm的矩阵,求这个矩阵中满足上下对称且左右对称的正方形子矩阵的个数。 1 ≤ n , m ≤ 1000 1\leq n,m\leq 1000 1≤n,m≤1000 题解 首先,我们对原矩阵、左右翻转后的矩阵、上下翻转后…...
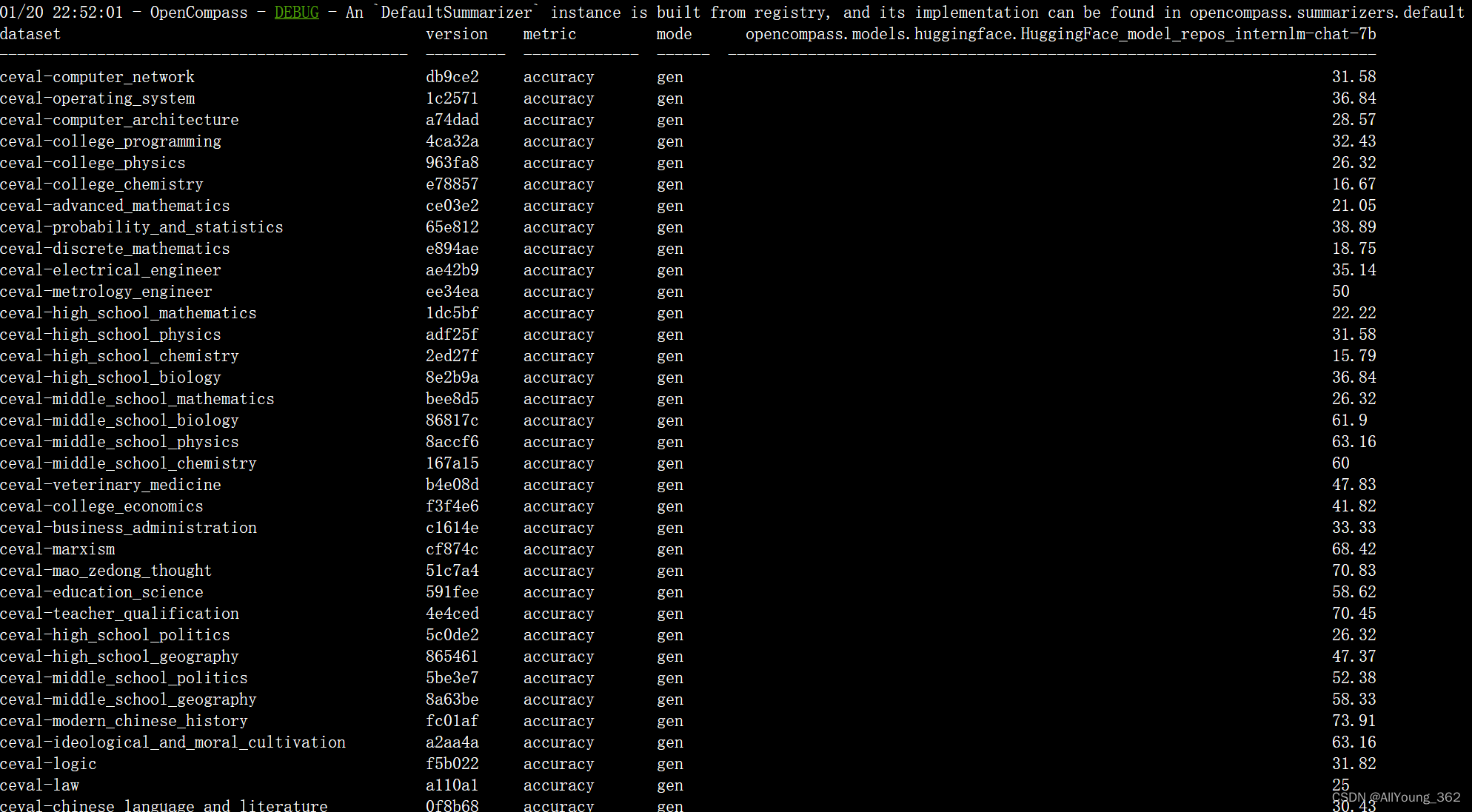
大模型学习与实践笔记(十一)
一、使用OpenCompass 对模型进行测评 1.环境安装: git clone https://github.com/open-compass/opencompass cd opencompass pip install -e . 当github超时无法访问时,可以在原命令基础上加上地址: https://mirror.ghproxy.com git clon…...
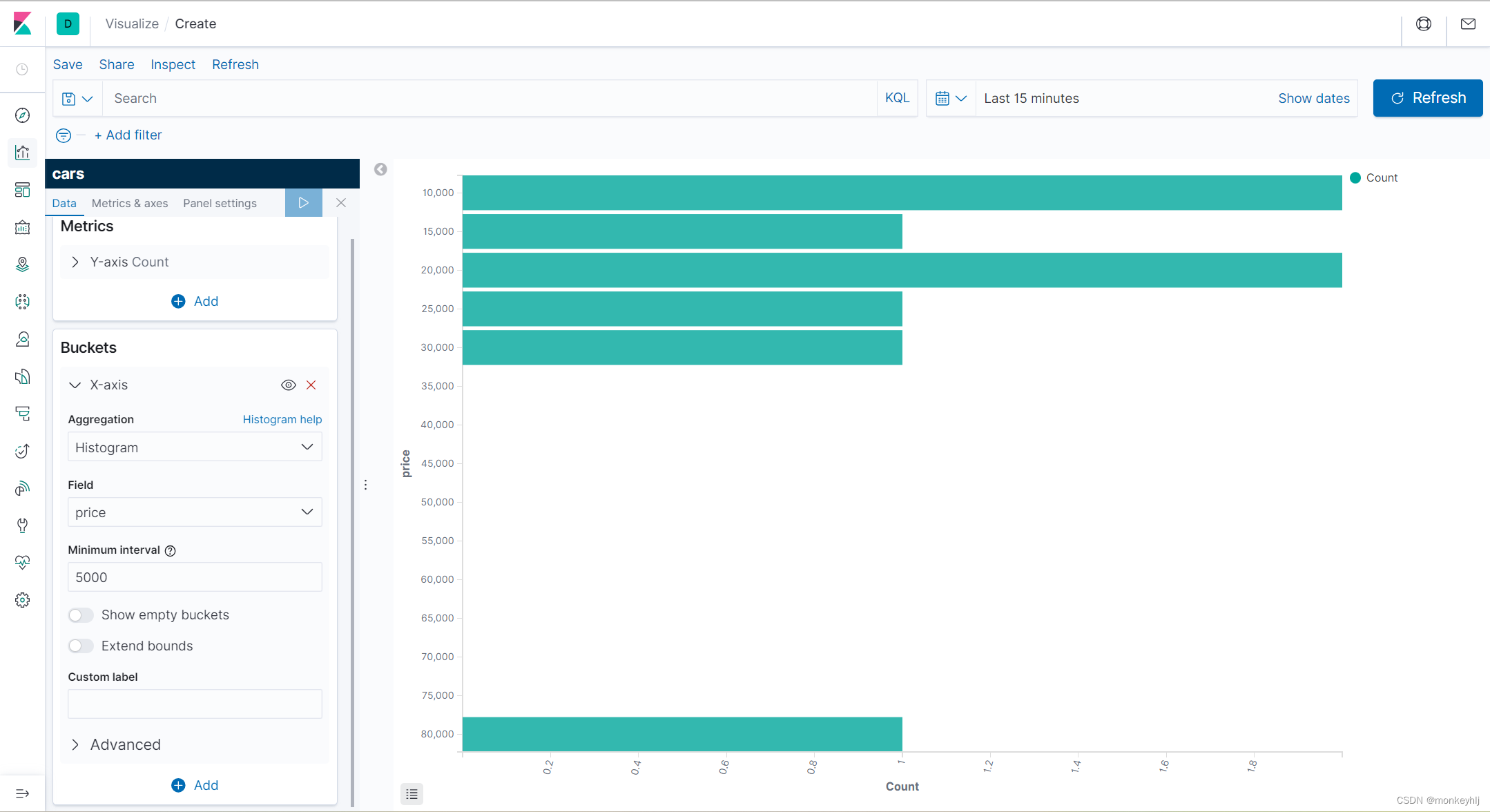
Elasticsearch+Kibana 学习记录
文章目录 安装Elasticsearch 安装Kibana 安装 Rest风格API操作索引基本概念示例创建索引查看索引删除索引映射配置(不配置好像也行、智能判断)新增数据随机生成ID自定义ID 修改数据删除数据 查询基本查询查询所有(match_all)匹配查…...

Cesium叠加超图二维服务、三维场景模型
前言 Cesium作为开源的库要加超图的服务则需要适配层去桥接超图与Cesium的数据格式。这个工作iClient系列已经做好,相比用过超图二维的道友们可以理解:要用Openlayer加载超图二维,那就用iClient for Openlayer库去加载;同样的要用…...

【低危】OpenSSL 拒绝服务漏洞
漏洞描述 OpenSSL 是广泛使用的开源加密库。 在 OpenSSL 3.0.0 到 3.0.12, 3.1.0 到 3.1.4 和 3.2.0 中 ,使用函数 EVP_PKEY_public_check() 来检查 RSA 公钥的应用程序可能会遇到长时间延迟。如果检查的密钥是从不可信任的来源获取的,这可能会导致拒绝…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
