<蓝桥杯软件赛>零基础备赛20周--第15周--快速幂+素数
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周。
在QQ群上交流答疑:

文章目录
- 1. 模运算
- 2. 快速幂
- 3. 素数
- 3.1 小素数的判定
- 3.2 素数筛
- 3.3 质因数分解
第14周: 快速幂+素数
蓝桥杯肯定考数学,例如数论、几何、概率论、组合数学等。这里介绍几个简单、常见的知识点。
1. 模运算
模运算是大数运算中的常用操作。如果一个数太大,无法直接输出,或者不需要直接输出,可以把它取模后,缩小数值再输出。
[ 模是Mod的音译,读作mó。Mod意为求余。]
定义取模运算为a除以m的余数,记为:a mod m = a % m
正整数取模的结果满足 0 ≤ a mod m ≤ m-1,其含义是用给定的m限制计算结果的范围。若m = 10,就是取a的个位数;若m = 2,余数为0,表示a为偶数,否则a为奇数。
一般的求余都是正整数的操作,如果是负数求余,不同的编程语言结果可能不同,下面给出三种语言的例子。
C和Java例子:(1)5 % 3,输出2;(2)(-5) % (-3),输出-2;(3)5 % (-3),输出2;(4)(-5) % 3,输出-2。计算规则是:先按正整数求余,然后加上符号,符号和被除数一样。
Python的负数求余有点奇怪,例如:(1)123 % 10,输出3;(2)123 %(-10),输出-7。原因是Python的求余是向下对齐的。
取模操作满足以下性质:
加:(a+b) mod m = ((a mod m) + (b mod m)) mod m。如果没有限制a、b的正负,C代码中左右可能符号相反、大小相差m。但是Python代码不存在这个问题。
减:(a - b) mod m = ((a mod m) – (b mod m)) mod m。C代码中左右可能符号相反、大小相差m。但是Python代码不存在这个问题。
乘:(a × b) mod m = ((a mod m) × (b mod m)) mod m
然而,对除法取模进行类似操作是错误的:(a/b) mod m = ((a mod m)/(b mod m)) mod m
例如,(100/50) mod 20 = 2,(100 mod 20) / (50 mod 20) mod 20 = 0,两者不相等。
2. 快速幂
一个常见的考点是做幂运算 a n a^n an,即n个a相乘,n一般极大,例如 n = 1 0 15 n=10^{15} n=1015。如果直接计算 a n a^n an,逐个相乘,那么要乘n次,肯定会超时。另外,由于 a n a^n an极大,一般会取模(求余数)再输出。
例题:快速幂
问题描述:给你三个整数a,n,m,求 a n a^n an mod m。
输入:输入只有一行三个整数,分别代表a,n,m。0≤a, b< 2 31 2^{31} 231,a+b>0,2≤p< 2 31 2^{31} 231。
输出:输出一行一个字符串 a^n mod m=s,其中a,n,m分别为题目给定的值,s为运算结果。
输入样例:
2 10 9
输出样例:
2^10 mod 9=7
容易想到一种很快的办法:先算 a 2 a^2 a2,然后再算平方 a 2 2 {a^2}^2 a22,再继续平方 a 2 2 2 {{a^2}^2}^2 a222,…总共只需要算O(logn)次,就得到了 a n a^n an。当 n = 1 0 15 n=10^{15} n=1015时,logn ≈ 50,计算量极小。不过这里的n需要是2的倍数,如果不是2的倍数呢?
下面先用分治法实现这个思路。分治法是一种“从宏观到微观”的处理方法。在快速幂这个问题中,把规模为n的大问题分解成两个完全一样的规模为n/2的子问题,子问题再继续分解,直到最后n=1,此时直接返回a即可。
下面是 a n % m a^n \% m an%m的分治法代码。注意第6、8、9行中”%m”的取模操作,如果不取模会导致溢出。
C++代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll; //用long long,比int的范围大
ll fastPow(ll a, ll n,ll m){ //a^n % mif(n == 0) return 1; //特判 a^0 = 1if(n == 1) return a % m;ll t = fastPow(a, n/2, m); //分治if(n%2 == 1) return (t % m * t % m) * a % m; //奇数个aelse return t % m * t % m ; //偶数个a
}
int main(){ll a,n,m; cin>>a>>n>>m; printf("%lld^%lld mod %lld=%lld",a,n,m,fastPow(a,n,m));return 0;
}
java代码
import java.util.Scanner;
public class Main {public static long fastPow(long a, long n, long m) {if (n == 0) return 1;if (n == 1) return a % m;long t = fastPow(a, n / 2, m);if (n % 2 == 1) return (t % m * t % m) * a % m;else return t % m * t % m;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);long a = sc.nextLong();long n = sc.nextLong();long m = sc.nextLong();System.out.printf("%d^%d mod %d=%d", a, n, m, fastPow(a, n, m));}
}
python代码
def fastPow(a, n, m):if n == 0: return 1if n == 1: return a % mt = fastPow(a, n//2, m)if n % 2 == 1: return (t * t) * a % melse: return t * t % m
a, n, m = map(int, input().split())
print(str(a) + '^' + str(n) + ' mod ' + str(m) + '=' + str(fastPow(a, n, m))) 读者可以用n=7来模拟代码的计算过程,了解它是如何处理n的,特别是n为奇数的情况。
这个代码已经很不错了,不过,标准的快速幂有更好的方法,用位运算实现。位运算实现快速幂的效率和分治法的效率一样,都是O(logn)的。
基于位运算的快速幂,用到了二进制数的性质,二进制数每一位的权值是按2的倍数递增的。下面以 a 11 a^{11} a11为例说明如何用倍增法做快速幂。
(1)幂次与二进制的关系。把 a 11 a^{11} a11分解成幂 a 8 a^8 a8、 a 2 a^2 a2、 a 1 a^1 a1的乘积: a 11 = a 8 + 2 + 1 = a 8 × a 2 × a 1 a^{11} = a^{8+2+1} = a^8 × a^2 × a^1 a11=a8+2+1=a8×a2×a1。其中 a 1 、 a 2 、 a 4 、 a 8 a^1、a^2、a^4、a^8 a1、a2、a4、a8…的幂次都是2的倍数,所有的幂ai都是倍乘关系,可以逐级递推,在代码中用 a *= a实现。
(2)幂次用二进制分解。如何把11分解为8+2+1?利用数的二进制的特征, n = 1 1 10 = 101 1 2 = 2 3 + 2 1 + 2 0 = 8 + 2 + 1 n = 11_{10} = 1011_2 = 2^3+2^1+2^0 = 8+2+1 n=1110=10112=23+21+20=8+2+1,只需要把n按二进制逐位处理就可以了。
(3)如何跳过那些没有的幂次?例如1011需要跳过 a 4 a^4 a4。做个判断即可,用二进制的位运算实现,用到了n & 1和n >>= 1这两个位运算。
n & 1:取n的最后一位,并且判断这一位是否需要跳过。
n >>= 1:把n右移一位,目的是把刚处理过的n的最后一位去掉。
以 n = 101 1 2 n=1011_2 n=10112为例,步骤如下:
n=1011,计算n & 1得1,最后一位是1,对应 a1。n >>= 1,右移一位,更新n=101。
n=101,计算n & 1得1,最后一位是1,对应 a2。n >>= 1,更新n=10。
n=10,计算n & 1得0,最后一位是0,跳过a4。n >>= 1,更新n=1。
n=1,计算n & 1得1,最后一位是1,对应a8。n >>= 1,更新n=0,结束。
下面是快速幂的代码。
C++代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll; //用long long,比int的范围大
ll fastPow(ll a, ll n, ll m){ll ans = 1;a %= m; //能在一定程度上防止下面的a*a越界while(n) {if(n & 1) ans = (ans*a) % m; //取模a = (a*a) % m; //取模n >>= 1;}return ans;
}
int main(){ll a,n,m; cin >> a >> n>> m; //m是模printf("%lld^%lld mod %lld=%lld",a,n,m,fastPow(a,n,m));return 0;
}
``java代码
```java
import java.util.Scanner;
public class Main {public static long fastPow(long a, long n, long m) {long ans = 1;a %= m;while (n > 0) {if ((n & 1) == 1) ans = (ans * a) % m;a = (a * a) % m;n >>= 1;}return ans;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);long a = sc.nextLong();long n = sc.nextLong();long m = sc.nextLong();System.out.printf("%d^%d mod %d=%d", a, n, m, fastPow(a, n, m));}
}
python代码
def fastPow(a, n, m):ans = 1while n:if n & 1: ans *= aa = (a * a) % mn >>= 1return ans % m
a, n, m = map(int, input().split())
print(str(a) + '^' + str(n) + ' mod ' + str(m) + '=' + str(fastPow(a, n, m)))
再做一题。
越狱
问题描述:监狱有n个房间,每个房间关押一个犯人,有m种宗教,每个犯人会信仰其中一种。如果相邻房间的犯人的宗教相同,就可能发生越狱,求有多少种状态可能发生越狱。答案对100,003取模。
输入:输入只有一行两个整数,分别代表宗教数m和房间数n。1≤m≤ 1 0 8 10^8 108, 1≤n≤ 1 0 12 10^{12} 1012。
输出:输出一行一个整数代表答案。
输入样例:
2 3
输出样例:
6
这是一道简单的组合数学问题。直接算越狱的方案数不方便,可以用总方案数减去不越狱的方案数,就是答案。
(1)总方案数。一个房间可以有m种宗教,所以n个房间一共有 m n m^n mn种方案。
(2)不越狱的方案数,就是任意两个相邻房间都不同的方案数。第1间有m种宗教;第2间不能和第1间相同,所以有m-1种;第3间还是有m-1种,因为它不能和第2间相同,但是可以和第1间相同;第4间、第5间、…、第n间也都是m-1种。所以不越狱的方案数一共是 m ( m − 1 ) n − 1 m(m-1)^{n-1} m(m−1)n−1。
答案是 m n − m ( m − 1 ) n − 1 m^n-m(m-1)^{n-1} mn−m(m−1)n−1,因为n很大,需要用快速幂计算。下面的代码,注意17~19行的取模处理。
C++代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll; //用long long,比int的范围大
ll fastPow(ll a, ll n, ll m){ll ans = 1;a %= m; //能在一定程度上防止下面的a*a越界while(n) {if(n & 1) ans = (ans*a) % m; //取模a = (a*a) % m; //取模n >>= 1;}return ans;
}
int main(){ll n,m; cin >> m>> n;ll mod = 100003;ll ans = fastPow(m,n,mod) - m%mod * fastPow(m-1,n-1,mod)%mod;if(ans<0) ans += mod; //ans可能是负的,变为正数ans %= mod;cout << ans;return 0;
}
java代码
import java.util.Scanner;
public class Main {public static long fastPow(long a, long n, long m) {long ans = 1;a %= m;while (n > 0) {if ((n & 1) == 1) ans = (ans * a) % m;a = (a * a) % m;n >>= 1;}return ans;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);long m = sc.nextLong();long n = sc.nextLong();long mod = 100003;long ans = fastPow(m, n, mod) - (m % mod) * fastPow(m - 1, n - 1, mod) % mod;if (ans < 0) ans += mod;ans %= mod;System.out.println(ans);}
}
python代码
def fastPow(a, n, m):ans = 1while n:if n & 1: ans *= aa = (a * a) % mn >>= 1return ans % m
m, n = map(int, input().split())
mod = 100003
ans = fastPow(m, n, mod) - m * fastPow(m - 1, n - 1, mod) % mod
if ans < 0: ans += mod
ans %= mod
print(ans)
3. 素数
素数(质数)是数论的基础内容,也是算法竞赛的常考知识点。下面介绍素数的判定、筛选、质因数分解的方法和代码。
3.1 小素数的判定
素数定义:只能被1和自己整除的正整数。前20个素数是:2、3、5、7、11、13、17、19、23、29、31、3741、4347、53、59、61、67、71。素数的分布并不稀疏,小于一亿的素数有576万个。
如何判断一个数n是不是素数?当 n ≤ 1 0 12 n ≤ 10^{12} n≤1012时,用试除法:用[2, n-1]内的所有数去试着除n,如果都不能整除,就是素数。
很容易发现,试除法可以优化,把 [ 2 , n − 1 ] [2, n-1] [2,n−1]缩小到 [ 2 , n ] [2,\sqrt{n}] [2,n]。因为如果n不是素数,那么它肯定有一个≤ n \sqrt{n} n的因子,证明如下:若n=a×b,设a≤b,那么肯定有a≤ n \sqrt{n} n。经过这个优化后,试除法的计算复杂度是O( n \sqrt{n} n), n ≤ 1 0 12 n ≤ 10^{12} n≤1012时够用。下面是代码。
C++代码
bool is_prime(long long n){if(n <= 1) return false; //1不是素数for(long long i=2; i <= sqrt(n); i++)if(n % i == 0) return false; //能整除,不是素数return true; //是素数
}
java代码
import java.util.Scanner;
public class Main {public static boolean isPrime(long n) {if (n <= 1) return false;for (long i = 2; i <= Math.sqrt(n); i++)if (n % i == 0) return false; return true;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);long n = sc.nextLong();if (isPrime(n)) System.out.println("is prime");else System.out.println("not prime");}
}
python代码
import math
def is_prime(n):if n <= 1: return Falsefor i in range(2, int(math.sqrt(n)) + 1): # sqrt(n)或n**0.5if n % i == 0: return Falsereturn True
n = int(input())
if is_prime(n): print("is prime")
else: print("not prime")
试除法还可以继续优化。 [ 2 , n ] [2,\sqrt{n}] [2,n]可以继续缩小,如果提前算出 [ 2 , n ] [2,\sqrt{n}] [2,n]内的所有素数,那么用这些素数来除n就行了,因为 [ 2 , n ] [2,\sqrt{n}] [2,n]中的合数已经被素数除过了。下一节的埃氏筛法就用到这一原理。
选数
问题描述:已知n 个整数a1、a2、…、an,以及1个整数k(k<n)。从n个整数中任选k个整数相加,可分别得到一系列的和。例如当n = 4, k= 3,4个整数分别为3、7、12、19时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:3+7+19=29。
输入:第一行两个空格隔开的整数n, k(1≤n≤ 20,k<n)。第二行n个整数,分别为a1、a2、…、an,1≤ai≤5×106。
输出:输出一个整数表示种类数。
输入样例:
4 3
3 7 12 19
输出样例:
1
本题是一道简单的综合题:DFS+素数判定。先用DFS从n个数中任选k个,然后求和并判断是否为素数。
从n个数中选k个,且这k个数没有顺序关系,这是组合问题。选数的思路是:
(1)选第1个数,这个数可以是n个数中的任何一个,设选了ai。i从1到n遍历。
(2)选第2个数,此时选位置i后面的数,因为这样做可以避免重复。例如样例的{3, 7, 12, 19},若当前的组合选了{3, 12},那么下一次只能选后面的19,不能回头选7,这样会重复,因为{3, 7, 12}这个组合在前面已经选过了。
(3)按上述方法选其他数,直到满k个。
下面的代码,请注意DFS是如何执行的。第18行dfs()继续选下一个数,并且下一个数的位置在已经选的数后面。
C++代码
#include<bits/stdc++.h>
using namespace std;
int n,k;
int a[25];
int ans; //如果担心 int不够,可以改为 long long
bool is_prime(int s){ //判断s是否为素数。s很小,用int够了if(s <= 1) return false;for(int i=2; i <= sqrt(s); i++)if(s % i == 0) return false;return true;
}
void dfs(int cnt, int sum, int p){ //选了cnt个,和为sum;下一个从a[p]开始选if(cnt == k){ //已经选了k个if(is_prime(sum)) ans++;return ;}for(int i = p; i < n; i++)dfs(cnt+1, sum+a[i], i+1); //继续选下一个,并且下一个在a[i]后面return ;
}
int main(){cin >> n >> k;for(int i=0; i<n; i++) cin >> a[i];dfs(0, 0, 0);cout << ans;return 0;
}
java代码
import java.util.Scanner;
public class Main {static int n, k;static int[] a;static int ans;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();k = sc.nextInt();a = new int[n];for (int i = 0; i < n; i++) a[i] = sc.nextInt(); dfs(0, 0, 0);System.out.println(ans);sc.close();}static boolean isPrime(int s) {if (s <= 1) return false;for (int i = 2; i <= Math.sqrt(s); i++) if (s % i == 0) return false; return true;}static void dfs(int cnt, int sum, int p) {if (cnt == k) {if (isPrime(sum)) ans++;return;}for (int i = p; i < n; i++) dfs(cnt + 1, sum + a[i], i + 1); }
}
python代码
n, k = map(int, input().split())
a = list(map(int, input().split()))
ans = 0
def is_prime(s):if s <= 1: return Falsefor i in range(2, int(s ** 0.5) + 1):if s % i == 0: return Falsereturn True
def dfs(cnt, sum, p):global ansif cnt == k:if is_prime(sum): ans += 1returnfor i in range(p, n):dfs(cnt + 1, sum + a[i], i + 1)
dfs(0, 0, 0)
print(ans)
3.2 素数筛
素数筛用来解决这个问题:给定正整数n,求2~n内所有的素数。
可以用上一节的素数判定方法,一个个地判断,计算复杂度是O()。这个计算量有点大,有没有更快的方法?
容易想到用“筛子”,把非素数筛掉,剩下的就是素数。例如用2去筛2~n内的数,一次可以把所有的偶数筛掉。
有两种素数筛:埃氏筛、欧拉筛。埃氏筛的计算复杂度是O(nloglogn);欧拉筛的复杂度是O(n),不可能更快了。埃氏筛的编码简单,一般情况下也够用。
埃氏筛的操作很简单。下面以初始数列{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}为例,说明它的操作步骤。
(1)记录最小的素数2,然后筛掉2的倍数,得{2, 3, 4 , 5, 6 , 7, 8 , 9, 10 , 11, 12 , 13}。
(2)记录下一个素数3,然后筛掉3的倍数,得{2, 3, 4 , 5, 6 , 7, 8 , 9 , 10 , 11, 12 , 13}。
(3)记录下一个素数5,然后筛掉5的倍数,得{2, 3, 4 , 5, 6 , 7, 8 , 9 , 10 , 11, 12 , 13}。
继续以上步骤,直到结束。
下面是代码,其中visit[i]记录数i的状态,如果visit[i] = true,表示它被筛掉了,不是素数。用prime[]存放素数,例如prime[1]=2,是第一个素数。
C++代码
const int N = 1e7; //定义空间大小,1e7约10M
int prime[N+1]; //存放素数,它记录visit[i] = false的项
bool visit[N+1]; //visit[i] = true表示i被筛掉,不是素数
int E_sieve(int n) { //埃氏筛法,计算[2, n]内的素数int k=0; //统计素数个数for(int i=0; i<=n; i++) visit[i]= false; //初始化for(int i=2; i<=n; i++) { //从第一个素数2开始。可优化(1)if(!visit[i]) {prime[++k] = i; //i是素数,存储到prime[]中for(int j=2*i; j<=n; j+=i) //i的倍数,都不是素数。可优化(2)visit[j] = true; //标记为非素数,筛掉}}return k; //返回素数个数
}
java代码
public class Main {public static int N = 10000000; // 定义空间大小,1e7约10M
public static int[] prime = new int[N + 1];
// 存放素数,它记录visit[i] = false的项
public static boolean[] visit = new boolean[N + 1];
// visit[i] = true表示i被筛掉,不是素数public static int E_sieve(int n) { // 埃氏筛法,计算[2, n]内的素数int k = 0; // 统计素数个数for (int i = 0; i <= n; i++) visit[i] = false; // 初始化for (int i = 2; i <= n; i++) { // 从第一个素数2开始。可优化(1)if (!visit[i]) {prime[++k] = i; // i是素数,存储到prime[]中for (int j = 2*i; j<=n; j+=i) //i的倍数都不是素数。优化(2)visit[j] = true; // 标记为非素数,筛掉}}return k; // 返回素数个数}public static void main(String[] args) {int n = 100;int primeCount = E_sieve(n);System.out.println("cnt of prime:" + primeCount);System.out.print("list of prime:");for (int i = 1; i <= primeCount; i++)
System.out.print(prime[i] + " "); }
}
python代码
N = 10000000 # 定义空间大小,1e7约10M
prime = [0] * (N + 1) # 存放素数,它记录visit[i] = false的项
visit = [False] * (N + 1) # visit[i] = True表示i被筛掉,不是素数
def E_sieve(n):k = 0 # 统计素数个数visit[0: n + 1] = [False] * (n + 1) # 初始化for i in range(2, n + 1): # 从第一个素数2开始。可优化(1)if not visit[i]:k += 1prime[k] = i # i是素数,存储到prime[]中for j in range(2*i, n+1, i): # i的倍数都不是素数。可优化(2)visit[j] = True # 标记为非素数,筛掉return k # 返回素数个数
n = 100
primeCount = E_sieve(n)
print("cnt of prime:", primeCount)
print("list of prime", end="")
for i in range(1, primeCount + 1): print(prime[i], end=" ")
上述代码有2处可以优化:
(1)用来做筛除的数2、3、5…等,最多到就 n \sqrt{n} n可以了。例如,求n = 100以内的素数,用2、3、5、7筛就足够了。其原理和试除法一样:非素数k,必定可以被一个小于等于 k \sqrt{k} k的素数整除,被筛掉。这个优化很大。
(2)for(int j=2*i; j<=n; j+=i) 中的j = 2*i优化为 j = i*i。例如i = 5时,2*5、3*5、4*5已经在前面i = 2, 3, 4的时候筛过了。这个优化较小。
下面给出优化后的代码。
C++代码
int E_sieve(int n) {for(int i = 0; i <= n; i++) visit[i]= false;for(int i = 2; i<=sqrt(n); i++) //筛掉非素数 if(!visit[i])for(int j=i*i; j<=n; j+=i) visit[j] = true; //标记为非素数
//下面记录素数int k=0; //统计素数个数for(int i = 2; i <= n; i++)if(!visit[i]) prime[++k] = i; //存素数,prime[1]=2, prime[2]=3...return k; //返回素数个数
}
java代码
public class Main {public static int N = 10000000; // 定义空间大小,1e7约10M
public static int[] prime = new int[N + 1];
// 存放素数,它记录visit[i] = false的项
public static boolean[] visit = new boolean[N + 1];
// visit[i] = true表示i被筛掉,不是素数public static int E_sieve(int n) {for (int i = 0; i <= n; i++) visit[i] = false;for (int i = 2; i <= Math.sqrt(n); i++) // 筛掉非素数if (!visit[i]) for (int j = i * i; j <= n; j += i)visit[j] = true; // 标记为非素数 // 下面记录素数int k = 0; // 统计素数个数for (int i = 2; i <= n; i++) if (!visit[i]) prime[++k] = i; // 存素数,prime[1]=2, prime[2]=3... return k; // 返回素数个数}public static void main(String[] args) {int n = 100;int primeCount = E_sieve(n);System.out.println("cnt of prime:" + primeCount);System.out.print("list of prime:");for (int i = 1; i <= primeCount; i++) System.out.print(prime[i] + " "); }
}
python代码
import math
N = 10000000 # 定义空间大小,1e7约10M
prime = [0] * (N + 1) # 存放素数,它记录visit[i] = false的项
visit = [False] * (N + 1) # visit[i] = True表示i被筛掉,不是素数
def E_sieve(n):for i in range(n + 1): visit[i] = Falsefor i in range(2, int(math.sqrt(n)) + 1): # 筛掉非素数if not visit[i]:for j in range(i * i, n + 1, i):visit[j] = True # 标记为非素数# 下面记录素数k = 0 # 统计素数个数for i in range(2, n + 1):if not visit[i]:k += 1prime[k] = i # 存素数,prime[1]=2, prime[2]=3...return k # 返回素数个数
n = 100
primeCount = E_sieve(n)
print("cnt of prime:", primeCount)
print("list of prime", end="")
for i in range(1, primeCount + 1): print(prime[i], end=" ") 埃氏筛的计算复杂度:2的倍数被筛掉,计算n/2次;3的倍数被筛掉,计算n/3次;5的倍数被筛掉,n/5次…;总计算量等于n/2+n/3+n/5+n/7+n/11+…,约为O(nloglogn)。计算量很接近线性的O(n),已经相当好了。
空间复杂度:代码用到了bool visit[N+1]数组,当N = 1 0 7 10^7 107时,约10M。由于埃氏筛只能用于处理约n= 1 0 7 10^7 107的问题,10M空间是够用的。
埃氏筛可以算出[2, n]内的素数,不过更常见的应用场景是计算[L, R]区间内的素数,L、R极大,但R-L较小,此时也可以用埃氏筛。见下面的例题。
素数密度
问题描述:给定区间[L,R] (1≤L≤R<231,R-L≤106),请计算区间中素数的个数。
输入:第一行,两个正整数L和R。
输出:一行,一个整数,表示区间中素数的个数。
输入样例:
2 11
输出样例:
5
简单的思路是先分别筛出[2, L]和[2, R]内各有多少个素数,然后两者相减,就是[L,R]内的素数个数。但是由于L和R最大是 2 31 2^{31} 231,用埃氏筛会超时。
由于R-L≤ 1 0 6 10^6 106很小,如果只在[L, R]范围内做素数筛,计算量很小。如何筛?前面提到,在[2, n]内做素数筛时,只用[2, n \sqrt{n} n]内的素数去筛就可以了。本题的的n是L、R, R \sqrt{R} R<50000,所以只需要先计算出50000以内的素数,然后用这些素数在[L, R]内筛去合数,剩下的就是素数。
还有一个编程问题需要解决。前面的埃氏筛代码,用visit[]数组记录被筛的情况,若visit[i] = true,表示数字i被筛去。本题的i< 2 31 2^{31} 231,如果仍然直接用visit[]数组记录,数组大小需要达到 2 31 2^{31} 231= 2G,空间肯定不够用。解决方案是记录在visit[1]~visit[R-L+1]中,visit[1]记录L是否被筛,visit[2]记录L+1是否被筛,…,visit[R-L+1]记录R是否被筛。相关代码见24~27行。
C++代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+1;
int prime[50000]; //存放素数,p[1]=2,p[2]=3...
bool vis[N+1]; //vis[i]=true表示被筛掉,i不是素数
int E_sieve(int n) {for(int i = 0; i <= n; i++) vis[i]= false;for(int i = 2; i<=sqrt(n); i++)if(!vis[i])for(int j=i*i; j<=n; j+=i) vis[j] = true;int k=0;for(int i = 2; i <= n; i++)if(!vis[i]) prime[++k] = i;return k;
}
int main(){int cnt = E_sieve(50000); //先筛出50000内的所有素数int L,R; cin >> L >> R;if(L==1) L=2; //特判L=1的情况,1不是素数,让L从2开始memset(vis,0,sizeof(vis)); //沿用vis,注意清空for(int i=1;i<=cnt;i++){ //用筛出来的素数,在[L,R]中再筛一次int p = prime[i];long long start; //注意要用long long,因为L+p可能超过intif((L+p-1)/p*p > 2*p) start = (L+p-1)/p*p;//定位到第一个被筛的数else start = 2*p;for(long long j=start;j<=R;j+=p) //用long long, j+=p可能超intvis[j-L+1]=true; //筛掉。和第10行一样}int ans=0;for(int i=1;i<=R-L+1;++i) //R-L+1为区间长度,区间内没被标记的数是素数if(!vis[i]) ans++;cout<<ans;
}
java代码
import java.util.Arrays;
import java.util.Scanner;
public class Main {public static final int N = 1000001;public static int[] prime = new int[50000];public static boolean[] vis = new boolean[N + 1];public static int E_sieve(int n) {Arrays.fill(vis, false);for (int i = 2; i * i <= n; i++) if (!vis[i]) for (int j = i * i; j <= n; j += i) vis[j] = true; int k = 0;for (int i = 2; i <= n; i++) if (!vis[i]) prime[++k] = i; return k;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);int cnt = E_sieve(50000);int L = sc.nextInt();int R = sc.nextInt();if (L == 1) L = 2; Arrays.fill(vis, false);for (int i = 1; i <= cnt; i++) {int p = prime[i];long start;if ((L + p - 1) / p * p > 2 * p) start = (L + p - 1) / p * p;else start = 2 * p; for (long j = start; j <= R; j += p) vis[(int)(j - L + 1)] = true; }int ans = 0;for (int i = 1; i <= R - L + 1; ++i) if (!vis[i]) ans++; System.out.println(ans);}
}
python代码
import math
def E_sieve(n):prime = []vis = [False] * (n+1)for i in range(2, int(math.sqrt(n))+1):if not vis[i]:for j in range(i*i, n+1, i): vis[j] = Truefor i in range(2, n+1):if not vis[i]: prime.append(i)return primeif __name__ == "__main__":prime = E_sieve(1000000)cnt = len(prime)L, R = map(int, input().split())if L == 1: L = 2vis = [False] * (R-L+1)for i in range(cnt):p = prime[i]if (L+p-1)//p*p > 2*p: start = (L+p-1)//p*pelse: start = 2*pfor j in range(start, R+1, p): vis[j-L] = Trueans = 0for i in range(R-L+1):if not vis[i]: ans += 1print(ans)
3.3 质因数分解
正整数n可以唯一地分解为有限个素数的乘积: n = p 1 c 1 p 2 c 2 . . . p m c m n = p_1^{c1}p_2^{c2}...p_m^{cm} n=p1c1p2c2...pmcm,其中 c i c_i ci都是正整数, p i p_i pi都是素数且从小到大。
分解质因子的简单方法也是试除法。求n的质因子:
(1)求最小质因子 p 1 p_1 p1。从小到大检查从2到 n \sqrt{n} n的所有数,如果它能整除n,就是最小质因子。然后连续用p1除n,目的是去掉n中的 p 1 p_1 p1,此时n更新为较小的 n 1 n_1 n1。
(2)再找 n 1 n_1 n1的最小质因子。从小到大检查从 p 1 p_1 p1到的所有数。从 p 1 p_1 p1开始,是因为 n 1 n_1 n1没有比 p 1 p_1 p1小的素因子,而且 n 1 n_1 n1的因子也是n的因子。
(3)继续步骤(2),直到结束。
最后,如果剩下一个大于1的数,那么它也是一个素数,是n的最大质因子。例如6119 = 29*211,找到29后,剩下的 n 1 n_1 n1=211,由于29≥ 211 \sqrt{211} 211,无法执行上面步骤(2),说明211无法继续分解,它是一个素数,也是质因子。
试除法的复杂度是O( n \sqrt{n} n),效率较低,不过一般也够用。
因数分解
问题描述:每个正整数都可以分解成素数的乘积,例如:6=2×3,20= 2 2 2^2 22×5。现在,给定一个正整数,请按要求输出它的因数分解式。
输入:输入第一行,包含一个正整数N。2≤N≤ 1 0 12 10^{12} 1012。
输出:输出一行,为的因数分解式。要求按质因数由小到大排列,乘号用星号*表示,且左右各空一格。当且仅当一个素数出现多次时,将它们合并为指数形式,用上箭头^表示,且左右不空格。
输入样例:
20
输出样例:
2^2 * 5
C++代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){ll n; cin>>n;for (ll i=2;i<= sqrt(n);i++) { //注意n是变化的ll cnt=0; // 记录质因数i的个数if (n%i==0) { // i是质因数while(n%i==0) { //把n中的i除尽n/=i; //更新ncnt++; }if (cnt==1) cout<<i; //如果i只有一个,不输出指数else cout<<i<<'^'<<cnt; //输出指数if (n>1) cout<<" * "; //如果不是最后一个质因数,输出乘号}}if (n>1) cout<<n; //没分解干净,输出剩下的质因数return 0;
}
java代码
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);long n = sc.nextLong(); for (long i = 2; i <= Math.sqrt(n); i++) {int cnt = 0;if (n % i == 0) {while (n % i == 0) {n /= i;cnt++;}if (cnt == 1) System.out.print(i);else System.out.print(i + "^" + cnt); if (n > 1) System.out.print(" * "); }} if (n > 1) System.out.print(n); sc.close();}
}
python代码
import math
n = int(input())
for i in range(2, int(math.sqrt(n)) + 1):cnt = 0if n % i == 0:while n % i == 0:n //= icnt += 1if cnt == 1: print(i, end='')else: print(i, '^', cnt, sep='', end='')if n > 1: print(' * ', end='')
if n > 1: print(n)
相关文章:

<蓝桥杯软件赛>零基础备赛20周--第15周--快速幂+素数
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周。 在QQ群上交流答疑&am…...
Opencv小项目——手势数字刷TIKTOK
写在前面: 很久没更新了,之前的实习的记录也算是烂尾了,但是好在自己的实习记录还是有的,最近也忙碌了很多,终于放假了,今天下午正好没事,闲来无事就随便做个小玩意吧。 思来想去ÿ…...
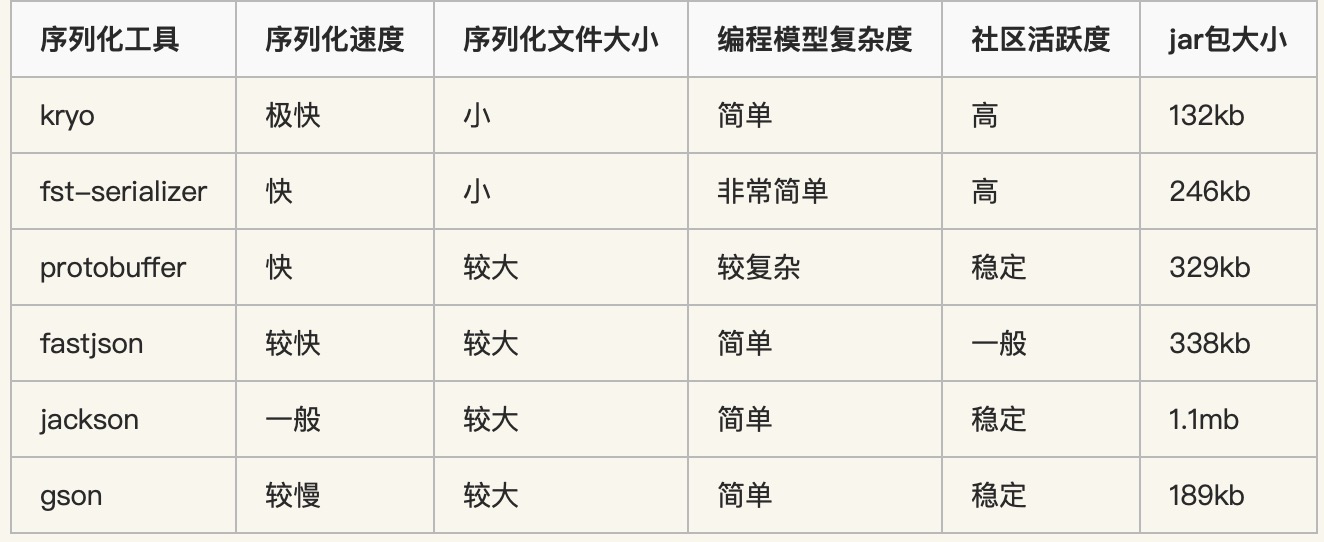
【优化技术专题】「性能优化系列」针对Java对象压缩及序列化技术的探索之路
针对Java对象压缩及序列化技术的探索之路 序列化和反序列化为何需要有序列化呢?Java实现序列化的方式二进制格式 指定语言层级二进制格式 跨语言层级JSON 格式化类JSON格式化:XML文件格式化 序列化的分类在速度的对比上一般有如下规律:Java…...
Spring+SprinMVC+MyBatis配置方式简易模板
SpringSprinMVCMyBatis配置方式简易模板代码Demo GitHub访问 ssm-tpl-cfg 一、SQL数据准备 创建数据库test,执行下方SQL创建表ssm-tpl-cfg /*Navicat Premium Data TransferSource Server : 127.0.0.1Source Server Type : MySQLSource Server Versio…...
Windows ssh登录eNSP交换机
目录 1. Cloud IO配置1.1 创建UDP端口1.2 创建本地连接1.3 端口映射设置 2. 交换机配置2.1 配置vlanif2.2 配置vty2.3 配置ssh用户2.4 配置aaa2.5 使用Xshell工具登录2.6 用户和密码2.7 登录成功 3. 使用cmd 登录报错提示3.1 手动指定加密算法,提示密码长度无效3.2 …...

SwiftUI 纯手工打造 100% 可定制的导航栏
功能需求 何曾几时,我们是否也厌倦了 SwiftUI 界面中刻板守旧的导航栏外观,而想要自己动手充分展示灵动炸裂的创造力呢? 如上图所示:我们在 SwiftUI 中通过纯手工打造了一款 100 在本篇博文中,您将学到以下内容 功能需求1. 导航栏基本结构2. 如何感知当前发生用户拖拽行为…...

npm install 太慢?解决方法
在使用npm进行包管理时,有时会遇到安装速度缓慢的问题。这可能是由于网络原因或npm官方镜像服务器的繁忙导致的。下面介绍几种常见的解决方法: 使用淘宝镜像 淘宝镜像是一个提供npm包镜像的国内源,其速度较快且稳定。您可以通过以下命令将npm…...

DevOps系列文章之 GitLab CI/CD
CICD是什么? 由于目前公司使用的gitlab,大部分项目使用的CICD是gitlab的CICD,少部分用的是jenkins,使用了gitlab-ci一段时间后感觉还不错,因此总结一下 介绍gitlab的CICD之前,可以先了解CICD是什么 我们的开发模式…...
)
【CompletableFuture任务编排】游戏服务器线程模型及其线程之间的交互(以排行榜线程和玩家线程的交互为例子)
需求: 1.我们希望玩家的业务在玩家线程执行,无需回调,因此是多线程处理。 2.匹配线程负责匹配逻辑,是单独一个线程。 3.排行榜线程负责玩家的上榜等。 4.从排行榜线程获取到排行榜列表后,需要给玩家发奖修改玩家数…...
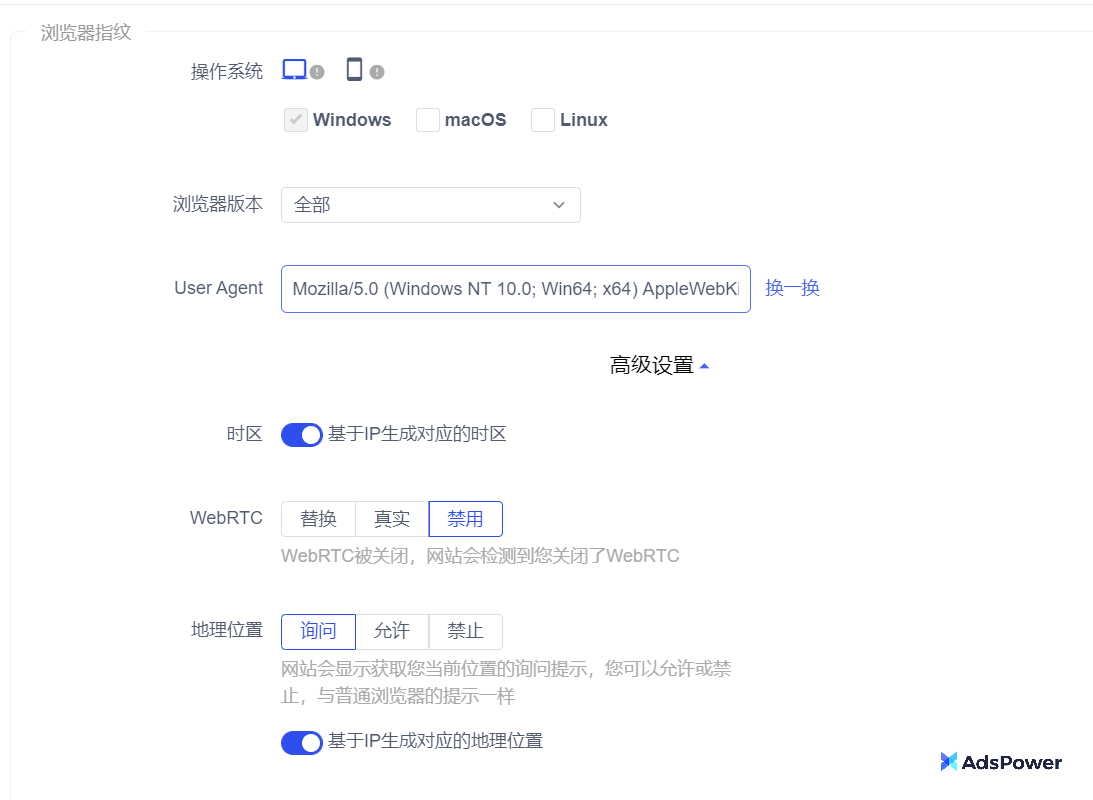
什么是浏览器指纹?详解浏览器指纹识别技术,教你防止浏览器指纹识别
在数字时代,我们的在线活动几乎总是留下痕迹。其中,浏览器指纹就像我们的数字身份证,让网站能够识别和追踪用户。对于跨境电商行业来说,了解这种追踪技术尤其重要,因为它可能影响账号的管理和安全。本文将详细介绍浏览…...

canvas绘制六芒星
查看专栏目录 canvas实例应用100专栏,提供canvas的基础知识,高级动画,相关应用扩展等信息。canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重…...

全网最详细!!Python 爬虫快速入门
1. 背景 最近在工作中有需要使用到爬虫的地方,需要根据 Gitlab Python 实现一套定时爬取数据的工具,所以借此机会,针对 Python 爬虫方面的知识进行了学习,也算 Python 爬虫入门了。 需要了解的知识点: Python 基础语…...
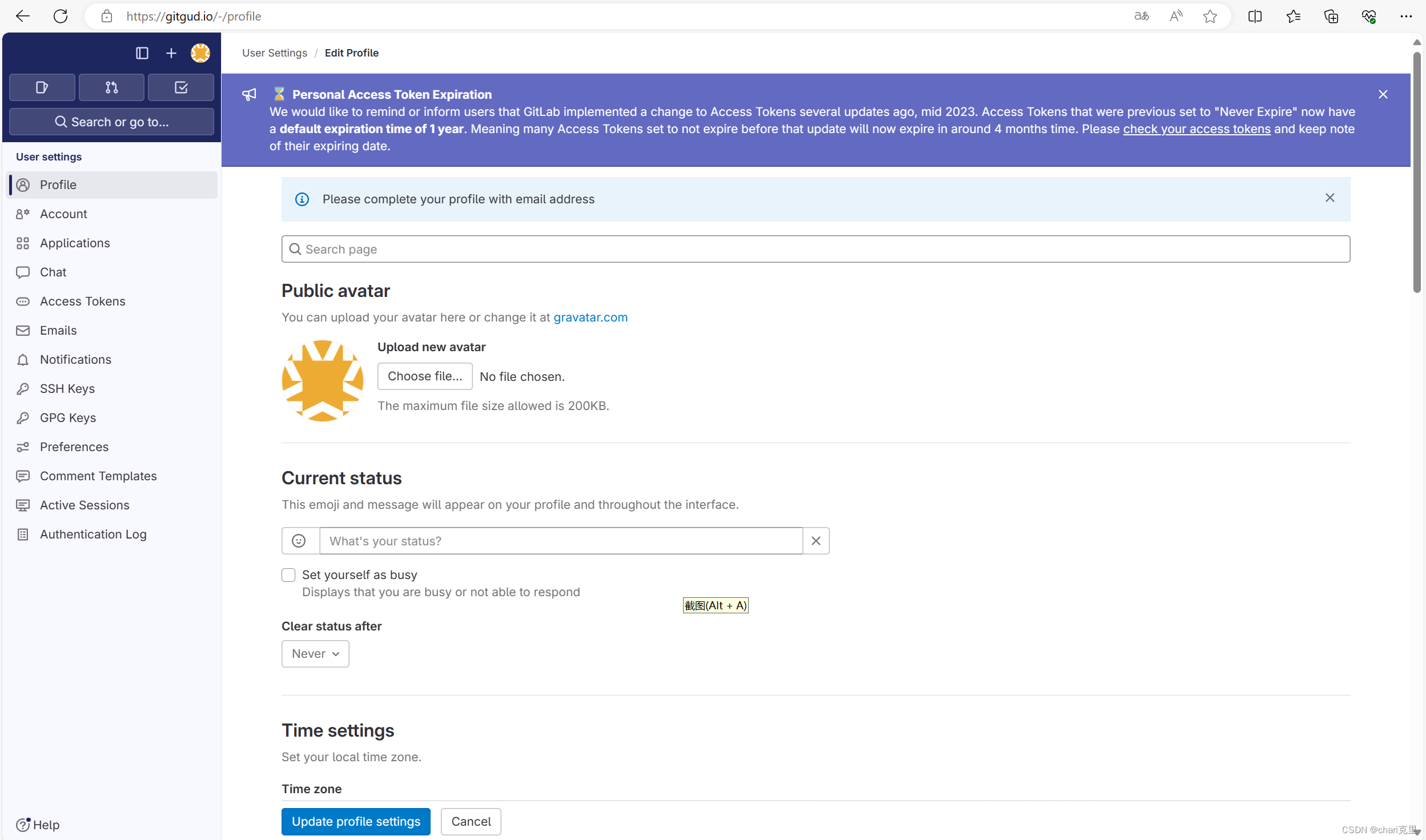
gitgud.io+Sapphire注册账号教程
gitgud.io是一个仓库,地址 https://gitgud.io/,点进去之后会看到注册页面。 意思是需要通过注册这个Sapphire账户来登录。点击右边的Sapphire,就跳转到Sapphire的登陆页面,点击创建新账号,就进入注册页面。࿰…...

【动态规划】【广度优先搜索】【状态压缩】847 访问所有节点的最短路径
作者推荐 视频算法专题 本文涉及知识点 动态规划汇总 广度优先搜索 状态压缩 LeetCode847 访问所有节点的最短路径 存在一个由 n 个节点组成的无向连通图,图中的节点按从 0 到 n - 1 编号。 给你一个数组 graph 表示这个图。其中,graph[i] 是一个列…...

python基础小知识:引用和赋值的区别
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 1.引用 python中,赋值操作会产生相同对象的多个引用, 如果在原位置修改这个可变对象时,可能会影响程序其他位置对这个对象的…...
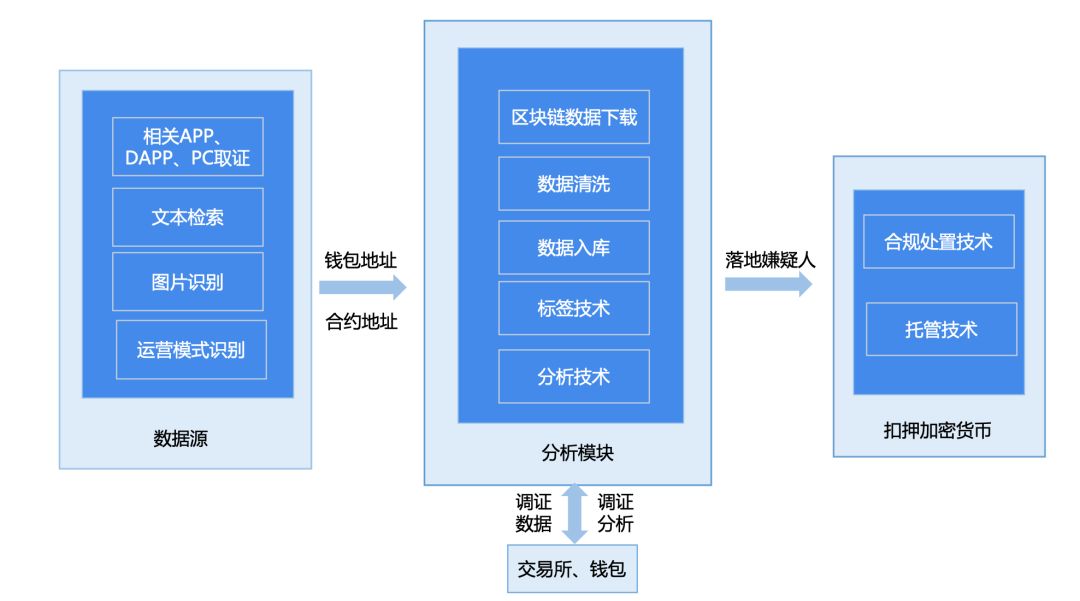
欧科云链与《警察技术》联合发布技术专题.pdf
欧科云链受《警察技术》邀请,于第201期期刊正式刊登“区块链生态安全与虚拟货币犯罪治理”技术专题。欧科云链作为该技术专题主要作者,直接参与本次期刊2篇文章撰写,同时为多篇文章提供欧科云链的最新数据和研究成果。 《警察技术》期刊创办于…...
【QT+QGIS跨平台编译】之一:【sqlite+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、sqlite3介绍二、文件下载三、文件分析四、pro文件五、编译实践 一、sqlite3介绍 SQLite是一款轻型的数据库,是遵守ACID的关系型数据库管理系统,它包含在一个相对小的C库中。它是D.RichardHipp建立的公有领域项目。它的设计目标是嵌入式的&…...
websocket实现聊天室(vue2 + node)
通过websocket实现简单的聊天室功能 需求分析如图: 搭建的项目结构如图: 前端步骤: vue create socket_demo (创建项目)views下面建立Home , Login组件路由里面配置路径Home组件内部开启websocket连接 前端相关组件代码: Login…...
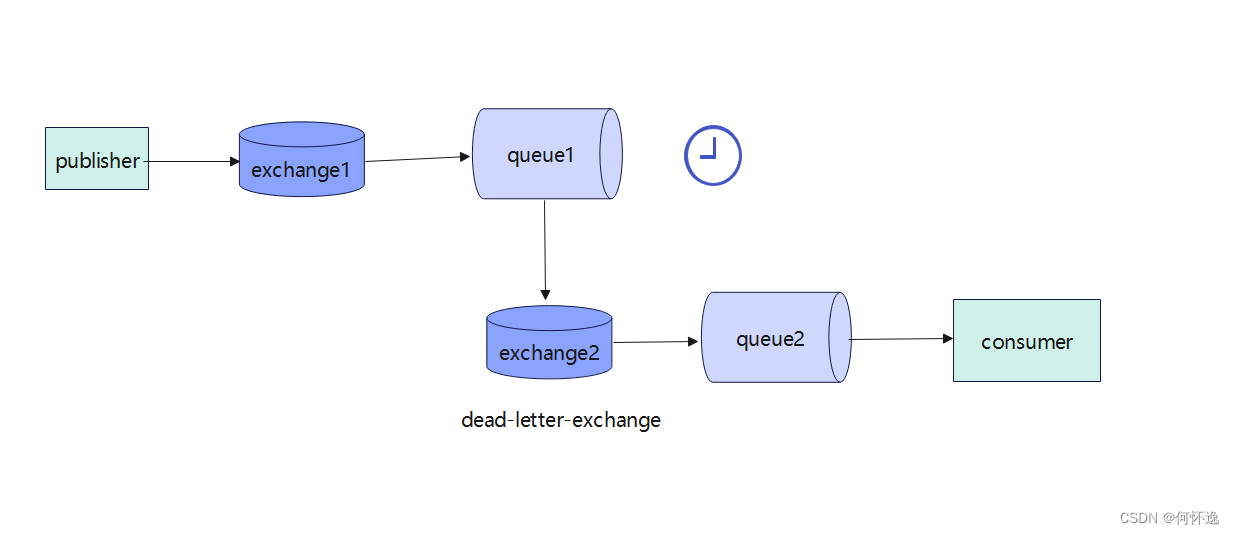
RabbitMQ-消息延迟
一、死信交换机 1、描述 一个队列接收到的消息有过期时间,消息过期之后,如果配置有死信队列,消息就会进去死信队列。 2、图解 3、过程 当生产者将消息发送到exchange1,然后交换机将消息路由到队列queue1,但是队列que…...

【Oracle】如何给物化视图分区
文章目录 【Oracle】如何给物化视图分区给物化视图进行分区的例 【声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和数据库技术(ID:SQLplusDB) 收集Oracle数据库内存相关的信息 【Oracle】ORA-32017和ORA-00384错误处理 【Oracle】设置…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...

组合模式:构建树形结构的艺术
引言:处理复杂对象结构的挑战 在软件开发中,我们常遇到需要处理部分-整体层次结构的场景: 文件系统中的文件与文件夹GUI中的容器与组件组织结构中的部门与员工菜单系统中的子菜单与菜单项组合模式正是为解决这类问题而生的设计模式。它允许我们将对象组合成树形结构来表示&…...
