【算法基础】前缀和与差分
😽PREFACE
🎁欢迎各位→点赞👍 + 收藏⭐ + 评论📝
📢系列专栏:算法
💪种一棵树最好是十年前其次是现在
1.什么是前缀和
前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身)。前缀和分为一维前缀和,以及二维前缀和。前缀和是一种重要的预处理,能够降低算法的时间复杂度。可以快速地求出某一段的和。
2.一维前缀和
2.1 前缀和公式
已知数组:
前缀和:
2.2 前缀和的作用


而且前缀和时间复杂度:预处理O(n),查询O(1),效率比较高效,后续也会有一些其他的解法,比如说线段树,树状数组等,前缀和的运行时间是最短的。
【补】关于左端边界是1的选择
我们会发现求l到r的和时,用的是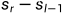 ,类似于数学里面的数列,此时令下标要l-1>=0,这就保证了
,类似于数学里面的数列,此时令下标要l-1>=0,这就保证了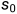 不需要定义任何的变量,使用起来比较简单
不需要定义任何的变量,使用起来比较简单
2.3 习题:前缀和

#include <iostream>
using namespace std;
const int N=1e5+10;
int n,m;
int a[N],s[N];
int main()
{scanf("%d %d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];//前缀和初始化while(m--){int l,r;scanf("%d %d",&l,&r);printf("%d\n",s[r]-s[l-1]);//区间和计算}return 0;}3.二维前缀和
3.1 二维前缀和公式
首先二维前缀和公式的成立是基于容斥定理的,二维前缀和实际上就是二维数组上的前缀和了。一维数组的前缀和也是一个一维数组,同样地,二维数组的前缀和也是一个二维的数组。

红色区域的和:
3.2 习题:子矩阵的和


这一子矩阵中的所有数之和为:
#include <iostream>
using namespace std;
const int N =1010;
int n,m,q;
int a[N][N],s[N][N];int main()
{scanf("%d %d %d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];//求前缀和while(q--){int x1,y1,x2,y2;scanf("%d %d %d %d",&x1,&y1,&x2,&y2);printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);//算子矩阵的和}return 0;
}4.什么是差分
类似于数学中的求导和积分,差分可以看成前缀和的逆运算。

5.一维差分
5.1 习题:差分

a数组是b数组的前缀和数组,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, ,a[n] + c;
然后我们还需要补充,b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,,a[n] - c;
我们画个图理解一下这个公式的由来:

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], b[N];
int main()
{scanf("%d %d", &n, &m);for (int i = 1; i <= n; i++){scanf("%d", &a[i]);b[i] = a[i] - a[i - 1];//构建差分数组}int l, r, c;while (m--){scanf("%d %d %d", &l, &r, &c);b[l] += c;//将[l,r]之间的每个数都加上cb[r + 1] -= c;}for (int i = 1; i <= n; i++){a[i] = b[i] + a[i - 1];//前缀和运算printf("%d ", a[i]);}return 0;
}5.2 时间复杂度的分析
如果采用暴力方法,用for循环l到r区间,时间复杂度O(n),如果我们需要对原数组执行m次这样的操作,时间复杂度就会变成O(n*m)。考虑差分做法可极大地降低复杂度。给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。
6.二维差分
6.1 习题:差分矩阵

#include <iostream>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],b[N][N];
int main()
{scanf("%d %d %d",&n,&m,&q);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];//同时求二维差分矩阵b,即将前缀和公式移项b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];}}while(q--){int x1,y1,x2,y2,c;cin>>x1>>y1>>x2>>y2>>c;//差分数组的模拟b[x1][y1]+=c;b[x1][y2+1]-=c;b[x2+1][y1]-=c;b[x2+1][y2+1]+=c;}//根据二维差分数组b去求二维前缀和矩阵afor(int i=1;i<=n;i++){for(int j=1;j<=m;j++){a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){printf("%d ",a[i][j]);}printf("\n");}return 0;}
6.2 差分矩阵的模拟
假定我们已经构造好了b数组,类比一维差分,我们执行以下操作来使被选中的子矩阵中的每个元素的值加上c:
b[x1][y1] + = c;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;每次对b数组执行以上操作,等价于:
for(int i=x1;i<=x2;i++)for(int j=y1;j<=y2;j++)a[i][j]+=c;图解过程:

b[x1][ y1 ] +=c ; //让整个a数组中矩形面积的元素都加上了c。
b[x1,][y2+1]-=c ; //让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y1]- =c ; //让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y2+1]+=c; //让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。相关文章:

【算法基础】前缀和与差分
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法💪种一棵树最好是十年前其次是现在1.什么是前缀和前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身&#x…...
LTD212次升级 | 官网社区支持PC端展示 • 官网新增证件查询应用,支持条形码扫码查询
1、新增证件查询应用,支持条形码扫码查询; 2、新增用户社区PC端功能; 01证件查询应用 1、新增证件查询应用功能 支持证件信息录入、打印功能,支持条形码扫码识别。 后台管理操作路径:官微中心 - 应用 - 证件查询 …...
【安全】nginx反向代理+负载均衡上传webshell
目录 一、负载均衡反向代理下上传webshell Ⅰ、环境搭建 ①下载蚁剑,于github获取官方版: ②下载docker&docker-compose ③结合前面启动环境 ④验证 负载均衡下webshell上传 一、负载均衡反向代理下上传webshell 什么是反向代理? 通常的代…...
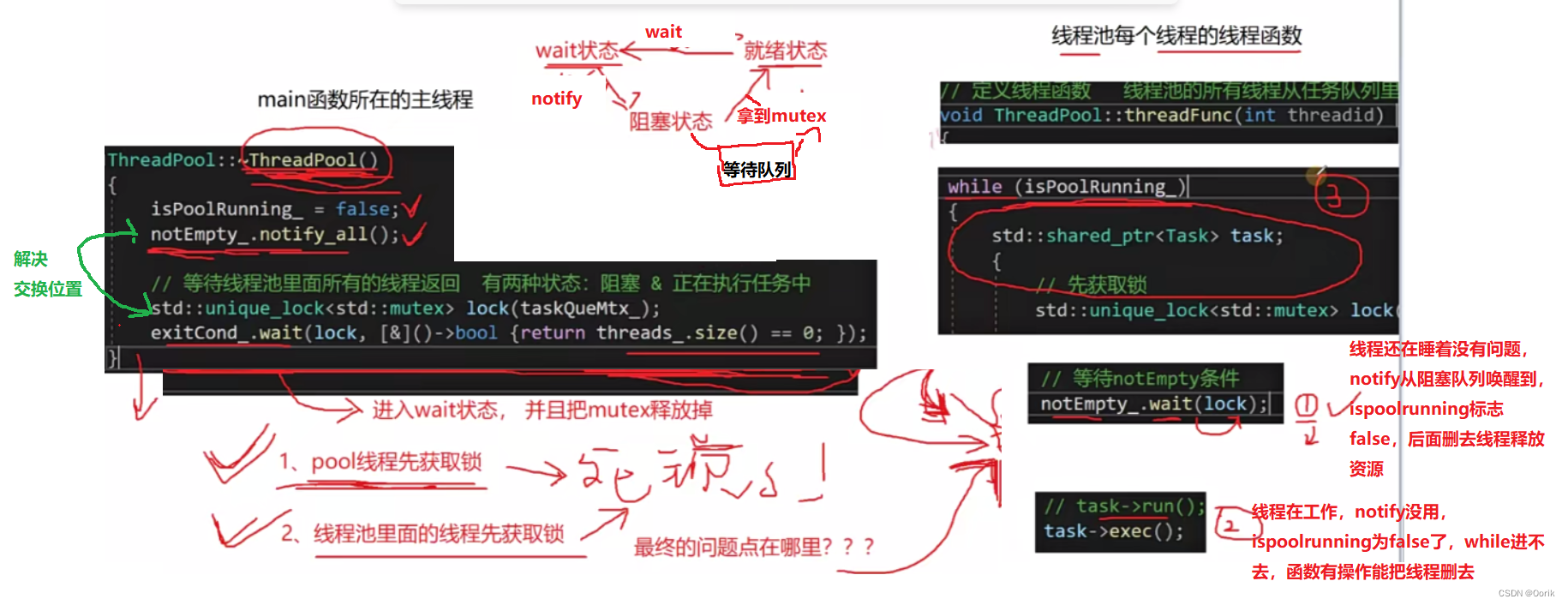
线程池框架
这是之前有做的一个可以接受用户传入任意类型的任务函数和任意参数,并且能拿到任务对应返回值的一个线程池框架,可以链接成动态库,用在相关项目里面。一共实现了两版,都是支持fixed和cached模式的,半同步半异步的&…...

【TCP的拥塞控制】基于窗口的拥塞控制
TCP的拥塞窗口CWND大小和传输轮次n的关系如下所示。(本题10分) cwnd12481632333435363738394041422122232425261248N1234567891011121314151617181920212223242526 问题: (1)慢开始阶段的时间间隔?&#…...
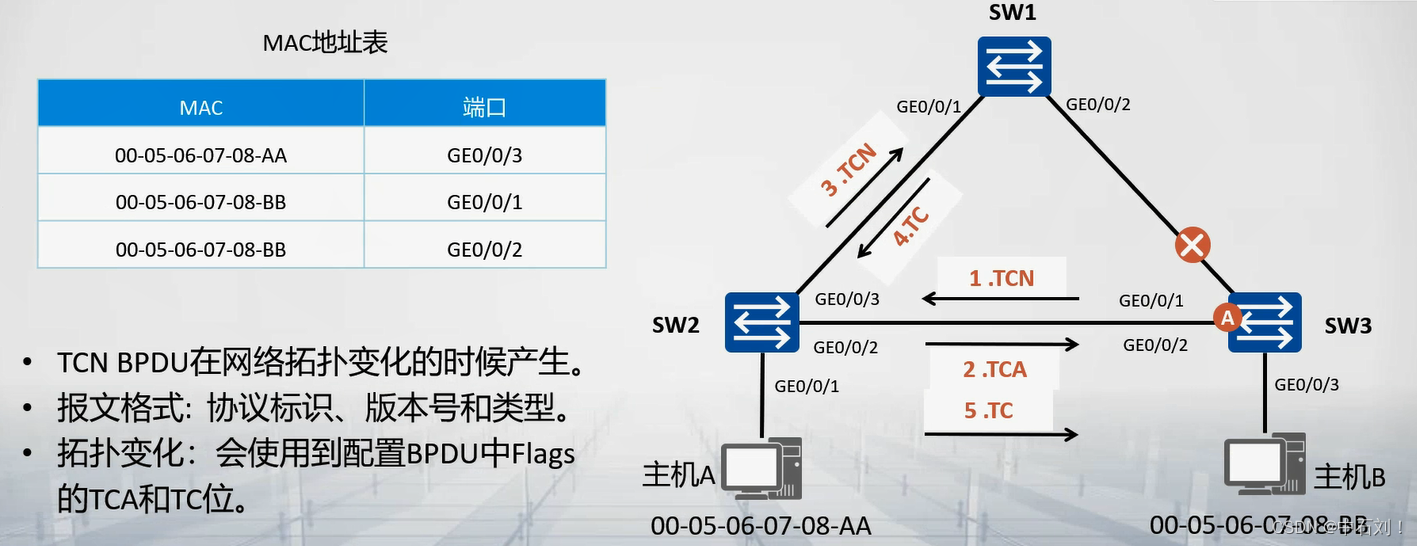
STP协议基础
STP协议技术来源二层环路及危害二层交换机网络的冗余性与环路人为错误导致的二层环路二层环路带来的问题STP生成树协议STP概述STP基本概念桥ID根桥COSTRPC(Root Path Cost)根路径开销PORT ID端口IDBPDU桥协议数据单元STP的计算过程(1…...
Linux上面配置Apache2支持Https(ssl)具体方案实现
虽然Nginx比较流行,但是由于一些老项目用到了Apache2来支持Web服务,最近想给服务上一个Https支持,虽然看似教程简单,但是也遇到一些特殊情况,经历了一番折腾也算是解决了所有问题,将过程记录如下。演示是基…...
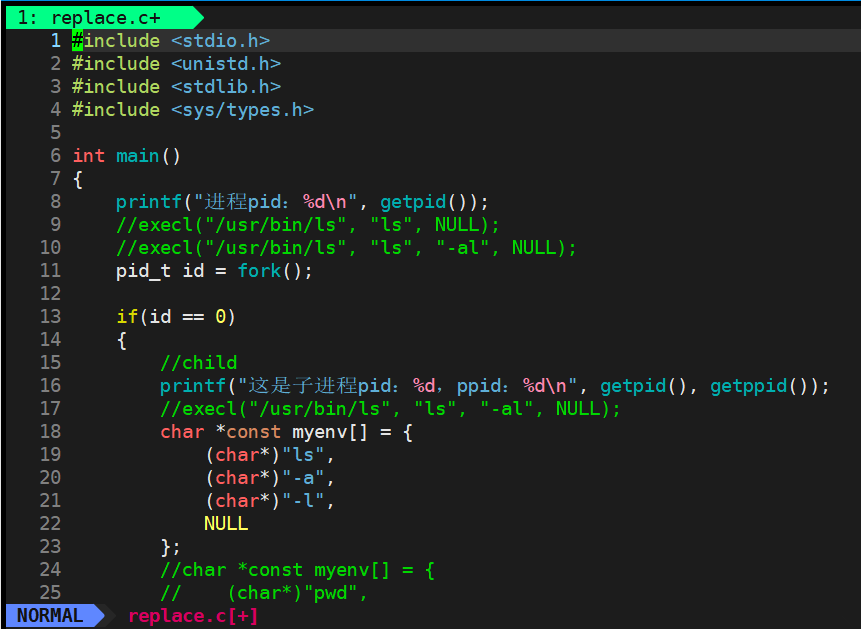
[Linux]进程替换
🥁作者: 华丞臧. 📕专栏:【LINUX】 各位读者老爷如果觉得博主写的不错,请诸位多多支持(点赞收藏关注)。如果有错误的地方,欢迎在评论区指出。 推荐一款刷题网站 👉 LeetCode刷题网站 文…...

常见的锁策略面试题
你是怎么理解乐观锁和悲观锁的,具体怎么实现呢? 悲观锁认为多个线程访问同一个共享变量冲突的概率较大, 会在每次访问共享变量之前都去真正加锁 乐观锁认为多个线程访问同一个共享变量冲突的概率不大. 并不会真的加锁, 而是直接尝试访问数据. 在访问的…...
设计师一定要知道这几个网站,解决你80%的设计素材。
本期推荐一波设计师必备的设计素材网站,设计党赶紧马住!能解决你日常设计中80%的素材。 1、菜鸟图库 菜鸟图库-免费设计素材下载 这是一个为新手设计师提供免费素材的设计网站,站内有超多平面模板、海报、UI设计、电商设计等相关素材&#x…...
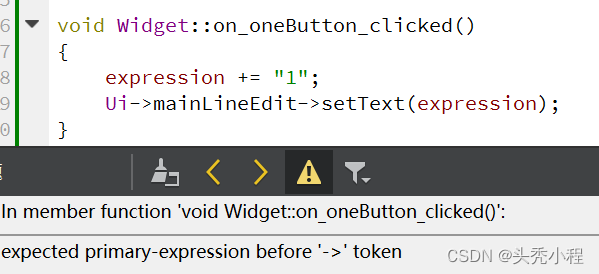
QT基础入门
学习视频:QT开发概述_哔哩哔哩_bilibili 1.QT开发概述 1.什么是QT QT是一个1991年由Qt Company开发的跨平台C图形用户界面应用程序开发框架。它既可以开发GUI程序,也可用于开发非GUI程序,比如控制台工具和服务器。Qt是面向对象的框架&#…...

高数不定积分72题解答
题目来源:这72道积分题目会积了,绝对是高高手 作者: 湖心亭看雪 第一题 原式∫15x3dx15∫15x3d(5x3)15ln(5x3)C\begin{aligned} \text{原式}&\int \frac{1}{5x3}dx \\ &\frac{1}{5} \int\frac{1}{5x3}d(5x3) \\ &\frac{1}{5} ln…...
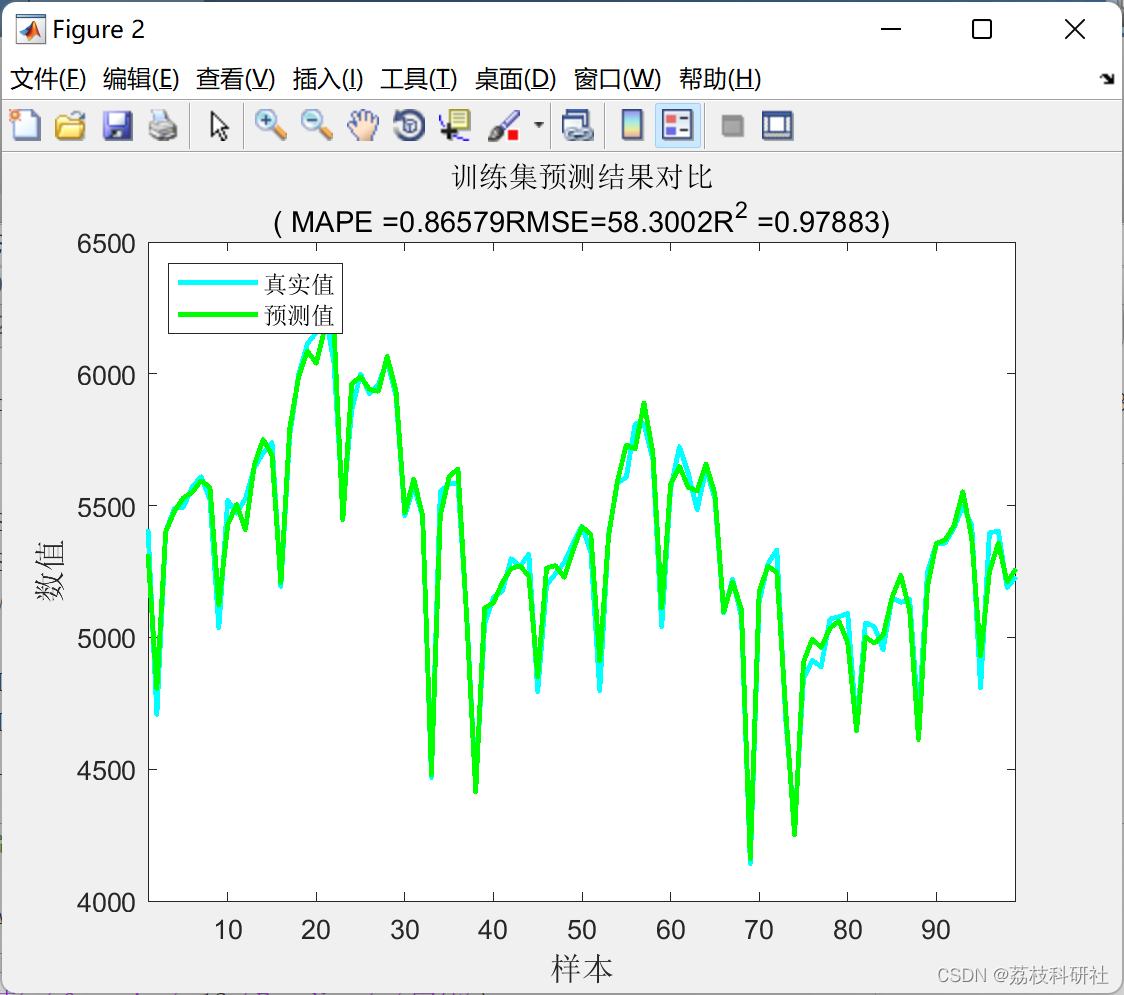
基于北方苍鹰算法优化LSTM(NGO-LSTM)研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Linux内核启动(理论,0.11版本)分段与分页
为什么要虚拟内存 我们知道,在之前上微机原理时,我们的程序是可以直接访问内存的,而且访问的是直接的物理内存,在实模式下,寄存器是16位的,数组总线(data bus)是16位的,…...

数据与C(字符串)
目录 一.概念引入 二.字符串(数组存储,必须以\0结尾) 三.错误示范 四.strlen()和sizeof()相对于字符串的不同 一.概念引入 “a”,a哪个是字符哪个又是字符串,嘿嘿不用猜了 我们在上一章中说过&#x…...

Python+Go实践(电商架构三)
文章目录服务发现集成consul负载均衡负载均衡算法实现配置中心nacos服务发现 我们之前的架构是通过ipport来调用的python的API,这样做的弊端是 如果新加一个服务,就要到某个服务改web(go)层的调用代码,配置IP/Port并发…...
基于 MySQL 排它锁实现分布式可重入锁解决方案
一、MySQL 排它锁和共享锁 在进行实验前,先来了解下MySQL 的排它锁和共享锁,在 MySQL 中的锁分为表锁和行锁,在行锁中锁又分成了排它锁和共享锁两种类型。 1. 排它锁 排他锁又称为写锁,简称X锁,是一种悲观锁&#x…...

【大数据】Hadoop-HA-Federation-3.3.1集群高可用联邦安装部署文档(建议收藏哦)
背景概述 单 NameNode 的架构使得 HDFS 在集群扩展性和性能上都有潜在的问题,当集群大到一定程度后,NameNode 进程使用的内存可能会达到上百 G,NameNode 成为了性能的瓶颈。因而提出了 namenode 水平扩展方案-- Federation。 Federation 中…...

【设计模式之美 设计原则与思想:面向对象】14 | 实战二(下):如何利用面向对象设计和编程开发接口鉴权功能?
在上一节课中,针对接口鉴权功能的开发,我们讲了如何进行面向对象分析(OOA),也就是需求分析。实际上,需求定义清楚之后,这个问题就已经解决了一大半,这也是为什么我花了那么多篇幅来讲…...

工作技术小结
2023/1/31 关于后端接口编写小结 1,了解小程序原型图流程和细节性的东西 2,数据库关联结构仔细分析,找到最容易查询的关键字段,标语表之间靠什么关联 2023/2/10 在web抓包过程中,如果要实现批量抓取,必须解…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...




