代码随想录算法训练DAY25|回溯2

算法训练DAY25|回溯2

216.组合总和III

力扣题目链接

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。

• 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

#思路

本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。

相对于77. 组合 ，无非就是多了一个限制，本题是要找到和为n的k个数的组合，而整个集合已经是固定的了[1,...,9]。

想到这一点了，做过77. 组合 之后，本题是简单一些了。

本题k相当于树的深度，9（因为整个集合就是9个数）就是树的宽度。

例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。

选取过程如图：

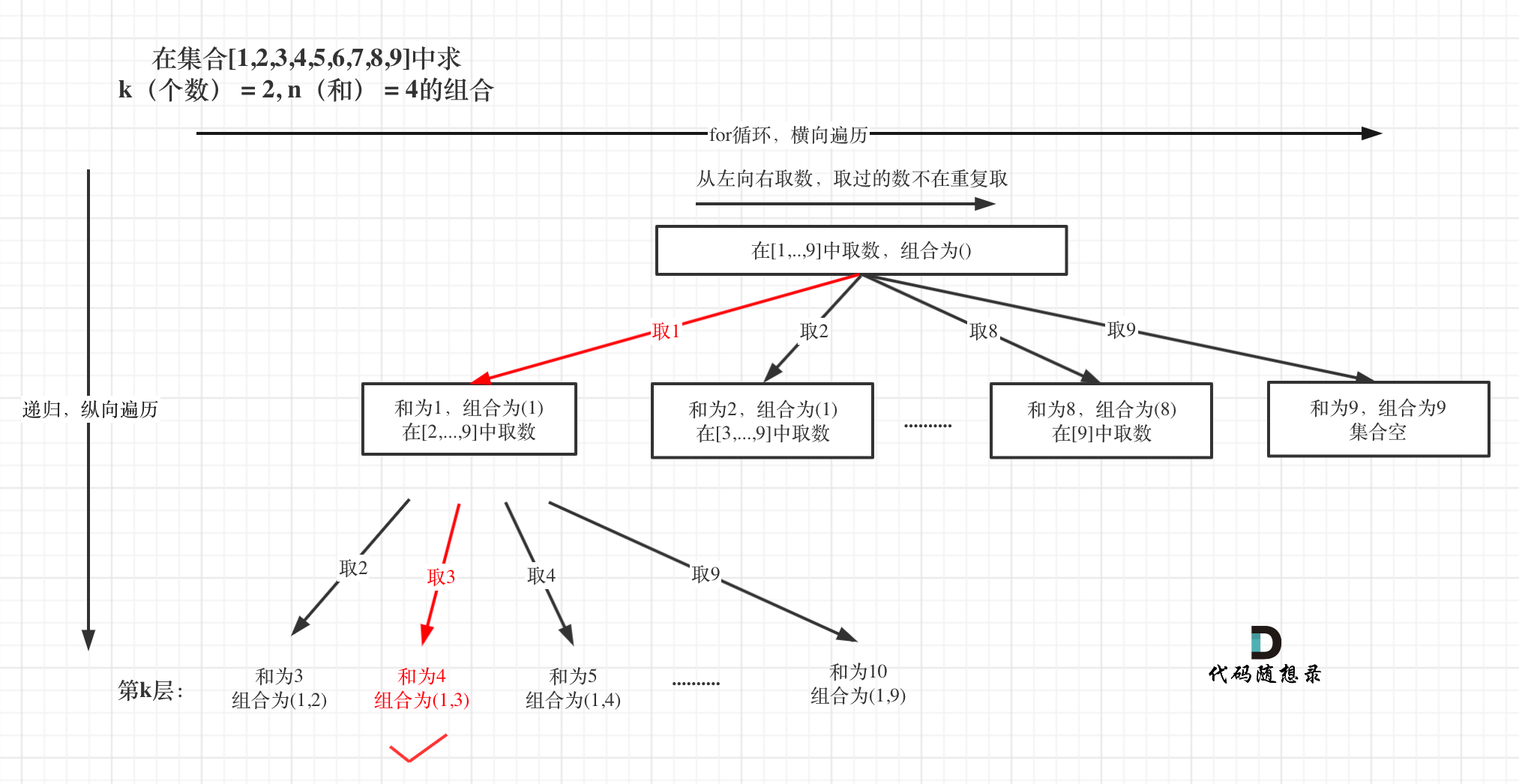
图中，可以看出，只有最后取到集合（1，3）和为4 符合条件。

#回溯三部曲

• 确定递归函数参数

和77. 组合 一样，依然需要一维数组path来存放符合条件的结果，二维数组result来存放结果集。

这里我依然定义path 和 result为全局变量。

至于为什么取名为path？从上面树形结构中，可以看出，结果其实就是一条根节点到叶子节点的路径。

vector<vector<int>> result; // 存放结果集
vector<int> path; // 符合条件的结果

接下来还需要如下参数：

• targetSum（int）目标和，也就是题目中的n。

• k（int）就是题目中要求k个数的集合。

• sum（int）为已经收集的元素的总和，也就是path里元素的总和。

• startIndex（int）为下一层for循环搜索的起始位置。

所以代码如下：

vector<vector<int>> result;
vector<int> path;
void backtracking(int targetSum, int k, int sum, int startIndex)

其实这里sum这个参数也可以省略，每次targetSum减去选取的元素数值，然后判断如果targetSum为0了，说明收集到符合条件的结果了，我这里为了直观便于理解，还是加一个sum参数。

还要强调一下，回溯法中递归函数参数很难一次性确定下来，一般先写逻辑，需要啥参数了，填什么参数。

• 确定终止条件

什么时候终止呢？

在上面已经说了，k其实就已经限制树的深度，因为就取k个元素，树再往下深了没有意义。

所以如果path.size() 和 k相等了，就终止。

如果此时path里收集到的元素和（sum） 和targetSum（就是题目描述的n）相同了，就用result收集当前的结果。

所以 终止代码如下：

if (path.size() == k) {if (sum == targetSum) result.push_back(path);return; // 如果path.size() == k 但sum != targetSum 直接返回
}

• 单层搜索过程

本题和77. 组合 区别之一就是集合固定的就是9个数[1,...,9]，所以for循环固定i<=9

如图：

处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和。

代码如下：

for (int i = startIndex; i <= 9; i++) {sum += i;path.push_back(i);backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.pop_back(); // 回溯
}

别忘了处理过程 和 回溯过程是一一对应的，处理有加，回溯就要有减！

参照关于回溯算法，你该了解这些！ 中的模板，不难写出如下C++代码：

class Solution {
private:vector<vector<int>> result; // 存放结果集vector<int> path; // 符合条件的结果// targetSum：目标和，也就是题目中的n。// k：题目中要求k个数的集合。// sum：已经收集的元素的总和，也就是path里元素的总和。// startIndex：下一层for循环搜索的起始位置。void backtracking(int targetSum, int k, int sum, int startIndex) {if (path.size() == k) {if (sum == targetSum) result.push_back(path);return; // 如果path.size() == k 但sum != targetSum 直接返回}for (int i = startIndex; i <= 9; i++) {sum += i; // 处理path.push_back(i); // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.pop_back(); // 回溯}}
​
public:vector<vector<int>> combinationSum3(int k, int n) {result.clear(); // 可以不加path.clear();   // 可以不加backtracking(n, k, 0, 1);return result;}
};

#剪枝

这道题目，剪枝操作其实是很容易想到了，想必大家看上面的树形图的时候已经想到了。

如图：

已选元素总和如果已经大于n（图中数值为4）了，那么往后遍历就没有意义了，直接剪掉。

那么剪枝的地方可以放在递归函数开始的地方，剪枝代码如下：

if (sum > targetSum) { // 剪枝操作return;
}

当然这个剪枝也可以放在 调用递归之前，即放在这里，只不过要记得 要回溯操作给做了。

for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝sum += i; // 处理path.push_back(i); // 处理if (sum > targetSum) { // 剪枝操作sum -= i; // 剪枝之前先把回溯做了path.pop_back(); // 剪枝之前先把回溯做了return;}backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.pop_back(); // 回溯
}

和回溯算法：组合问题再剪剪枝 一样，for循环的范围也可以剪枝，i <= 9 - (k - path.size()) + 1就可以了。

最后C++代码如下：

class Solution {
private:vector<vector<int>> result; // 存放结果集vector<int> path; // 符合条件的结果void backtracking(int targetSum, int k, int sum, int startIndex) {if (sum > targetSum) { // 剪枝操作return; }if (path.size() == k) {if (sum == targetSum) result.push_back(path);return; // 如果path.size() == k 但sum != targetSum 直接返回}for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝sum += i; // 处理path.push_back(i); // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.pop_back(); // 回溯}}
​
public:vector<vector<int>> combinationSum3(int k, int n) {result.clear(); // 可以不加path.clear();   // 可以不加backtracking(n, k, 0, 1);return result;}
};

• 时间复杂度: O(n * 2^n)

• 空间复杂度: O(n)

17.电话号码的字母组合

力扣题目链接

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:

• 输入："23"

• 输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

#思路

从示例上来说，输入"23"，最直接的想法就是两层for循环遍历了吧，正好把组合的情况都输出了。

如果输入"233"呢，那么就三层for循环，如果"2333"呢，就四层for循环.......

大家应该感觉出和77.组合 遇到的一样的问题，就是这for循环的层数如何写出来，此时又是回溯法登场的时候了。

理解本题后，要解决如下三个问题：

1. 数字和字母如何映射

2. 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来

3. 输入1 * #按键等等异常情况

#数字和字母如何映射

可以使用map或者定义一个二维数组，例如：string letterMap[10]，来做映射，我这里定义一个二维数组，代码如下：

const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9
};

#回溯法来解决n个for循环的问题

例如：输入："23"，抽象为树形结构，如图所示：

图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果，输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。

回溯三部曲：

• 确定回溯函数参数

首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。

这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。

代码如下：

vector<string> result;
string s;
void backtracking(const string& digits, int index)

• 确定终止条件

例如输入用例"23"，两个数字，那么根节点往下递归两层就可以了，叶子节点就是要收集的结果集。

那么终止条件就是如果index 等于 输入的数字个数（digits.size）了（本来index就是用来遍历digits的）。

然后收集结果，结束本层递归。

代码如下：

if (index == digits.size()) {result.push_back(s);return;
}

• 确定单层遍历逻辑

首先要取index指向的数字，并找到对应的字符集（手机键盘的字符集）。

然后for循环来处理这个字符集，代码如下：

int digit = digits[index] - '0';        // 将index指向的数字转为int
string letters = letterMap[digit];      // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {s.push_back(letters[i]);            // 处理backtracking(digits, index + 1);    // 递归，注意index+1，一下层要处理下一个数字了s.pop_back();                       // 回溯
}

注意：输入1 * #按键等等异常情况

代码中最好考虑这些异常情况，但题目的测试数据中应该没有异常情况的数据，所以我就没有加了。

但是要知道会有这些异常，如果是现场面试中，一定要考虑到！

// 版本一
class Solution {
private:const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9};
public:vector<string> result;string s;void backtracking(const string& digits, int index) {if (index == digits.size()) {result.push_back(s);return;}int digit = digits[index] - '0';        // 将index指向的数字转为intstring letters = letterMap[digit];      // 取数字对应的字符集for (int i = 0; i < letters.size(); i++) {s.push_back(letters[i]);            // 处理backtracking(digits, index + 1);    // 递归，注意index+1，一下层要处理下一个数字了s.pop_back();                       // 回溯}}vector<string> letterCombinations(string digits) {s.clear();result.clear();if (digits.size() == 0) {return result;}backtracking(digits, 0);return result;}
};

• 时间复杂度: O(3^m * 4^n)，其中 m 是对应四个字母的数字个数，n 是对应三个字母的数字个数

• 空间复杂度: O(3^m * 4^n)

一些写法，是把回溯的过程放在递归函数里了，例如如下代码，我可以写成这样：（注意注释中不一样的地方）

// 版本二
class Solution {
private:const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9};
public:vector<string> result;void getCombinations(const string& digits, int index, const string& s) { // 注意参数的不同if (index == digits.size()) {result.push_back(s);return;}int digit = digits[index] - '0';string letters = letterMap[digit];for (int i = 0; i < letters.size(); i++) {getCombinations(digits, index + 1, s + letters[i]);  // 注意这里的不同}}vector<string> letterCombinations(string digits) {result.clear();if (digits.size() == 0) {return result;}getCombinations(digits, 0, "");return result;
​}
};

我不建议把回溯藏在递归的参数里这种写法，很不直观，我在二叉树：以为使用了递归，其实还隐藏着回溯 这篇文章中也深度分析了，回溯隐藏在了哪里。

所以大家可以按照版本一来写就可以了。