【C语言深度剖析——第四节(关键字4)】《C语言深度解剖》+蛋哥分析+个人理解
追求本质,不断进步
本文由@睡觉待开机原创,转载请注明出处。
本内容在csdn网站首发
欢迎各位点赞—评论—收藏
如果存在不足之处请评论留言,共同进步!
这里写目录标题
- 一、空间的申请
- 1.变量定义
- 1.1变量定义的概念:
- 1.2变量定义的原因:
- 2.变量声明
- 二、数据存入
- 1.转换补码
- 2.大小端存储
- 3.截断
- 4.取值范围的问题
- 三、数据取出
- 1.大小端
- 2.自身类型
- 3.整型提升
- 练习题
前言:
本节博客继续前篇内容进行续写,我们着重探求有符号与无符号数的问题,探求整形在内存中的存储这一课题
一、空间的申请
1.变量定义
1.1变量定义的概念:
所谓变量定义,本质上就是在内存中开辟特定大小的空间(不做解释,后文体会)。
概念区分:初始化与赋值
(1)概念:
初始化:指的是变量与生俱来的内容属性
赋值:值的是变量后来放到该变量空间的内容属性
(2)特点:
初始化只能进行一次,赋值可以进行多次
初始化具有先天性的含义,赋值有着后天的含义。
1.2变量定义的原因:
定义变量的原因在于开辟空间,暂时存储数据
首先,我们需要明确的是计算机是弥补人类计算能力低下问题诞生的(这里并没有贬低人类的意思,就是说人类跟计算机相比计算能力确实相对来说比较差)
之后,我们需要明白,我们人类计算时候是需要一步一步计算的,计算机也是需要进行先后计算了,并不是一下子就对所有数据进行处理,计算机也是对一个一个数据进行依次处理的,至于为什么算个数字那么快,因为计算机算的快而已,这并不是说计算机对所有数据进行同时处理。(注:当然计算机也是可以同时对数据进行处理的,不过同时处理数据的能力有限,了解即可)
然后,我们大概就明白了,为何需要变量?就是因为有些数据需要等待一些时间去让计算机处理,在处理之前,需要先存储起来防止数据丢失,这大概跟人类做运算时候要写在纸上差不多,省的忘了原来的数据,如果忘了那就惨了。
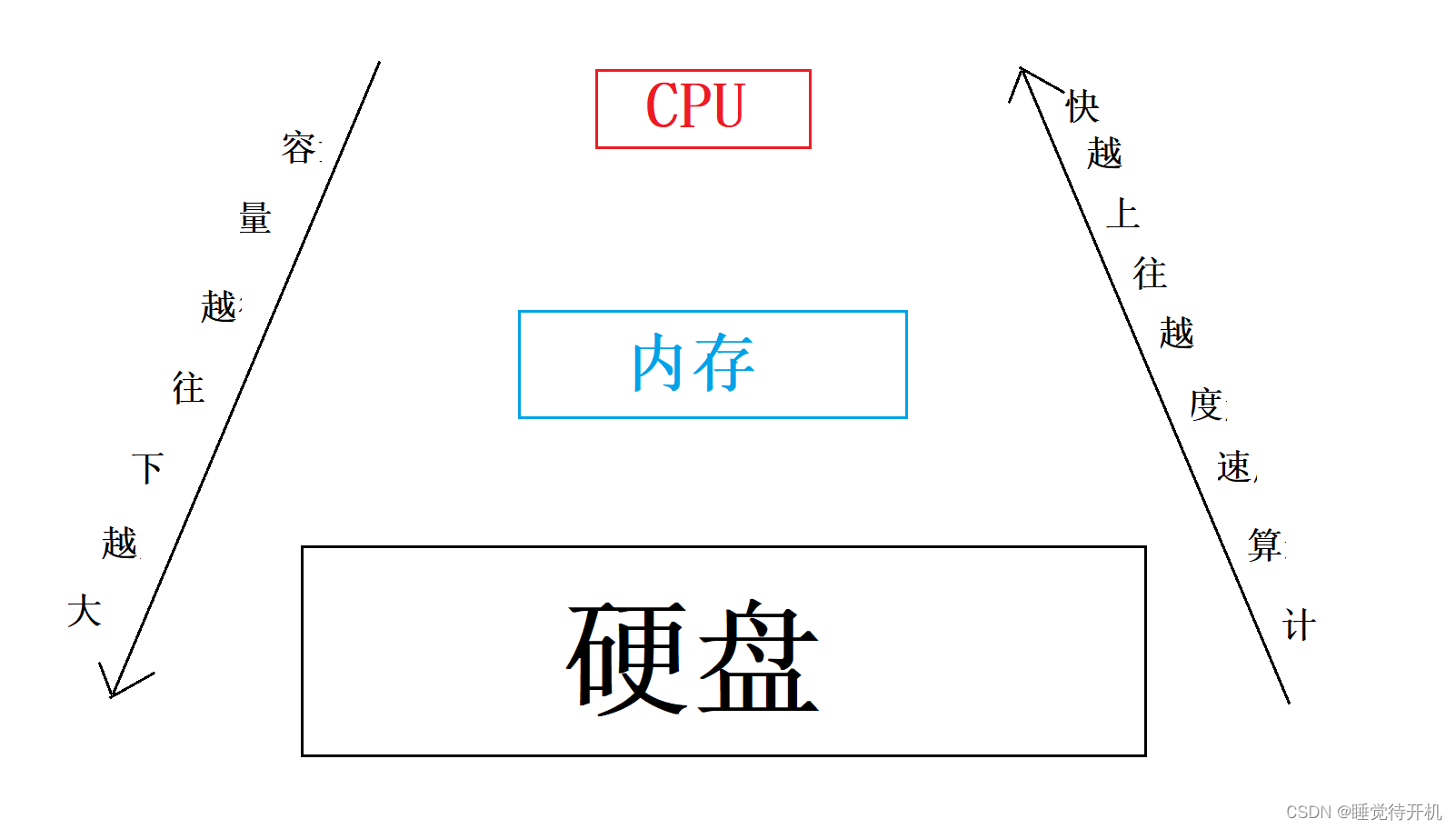
那为啥需要把数据放在一个个变量里进行处理啊?我数据直接放那一团不就行了嘛,这有点类似于我们吃饭,我们一般都是用碗吃饭,而不是直接用锅,原因在于效率高,计算机也是一样,在处理数据的时候,先用变量把在“一锅里的”数据分到一个个小碗里,然后就“吃”的快了。而且之前讲过,我们做饭的地方跟我们吃饭的地方离得距离是比较远的,类似于硬盘中的程序跟cpu处理是比较远的,要想提高效率,就是借助变量变成“小碗”送到内存当中,这样就跟cpu离得近了。其实我感觉变量就是起到了一个方便读取数据的作用。
变量定义的本质在于,开辟一块内存空间,暂时存储数据
2.变量声明
变量声明的本质就是:告知编译器。**
两者的区别在于,
声明你可以声明多次,定义只能定义一次哈。
本质区别在于定义开辟内存空间,变量声明没有开辟内存空间。
这个区别有一个比较有意思的比喻,大概是这样的,变量的定义类似于你跟你女朋友表白,只能表白一次吧?哈哈。然后变量的声明的话就是你告诉你周围的人,那个女孩是我女朋友哈,你们不要有非分之想了哈。这里想说声明可以声明无数次。(这里只是做一个比喻说明一下哈,无任何不良诱导)
二、数据存入
首先同学们,我想问int a = -10;计算机会直接把-10存入内存中吗?答案是不是
原因在于计算机只认识二进制。
因而就需要进制转换,需要把-10这一个十进制数字转换成为二进制的形式,这就牵扯到了原码、反码以及补码的概念和转换问题。
1.转换补码
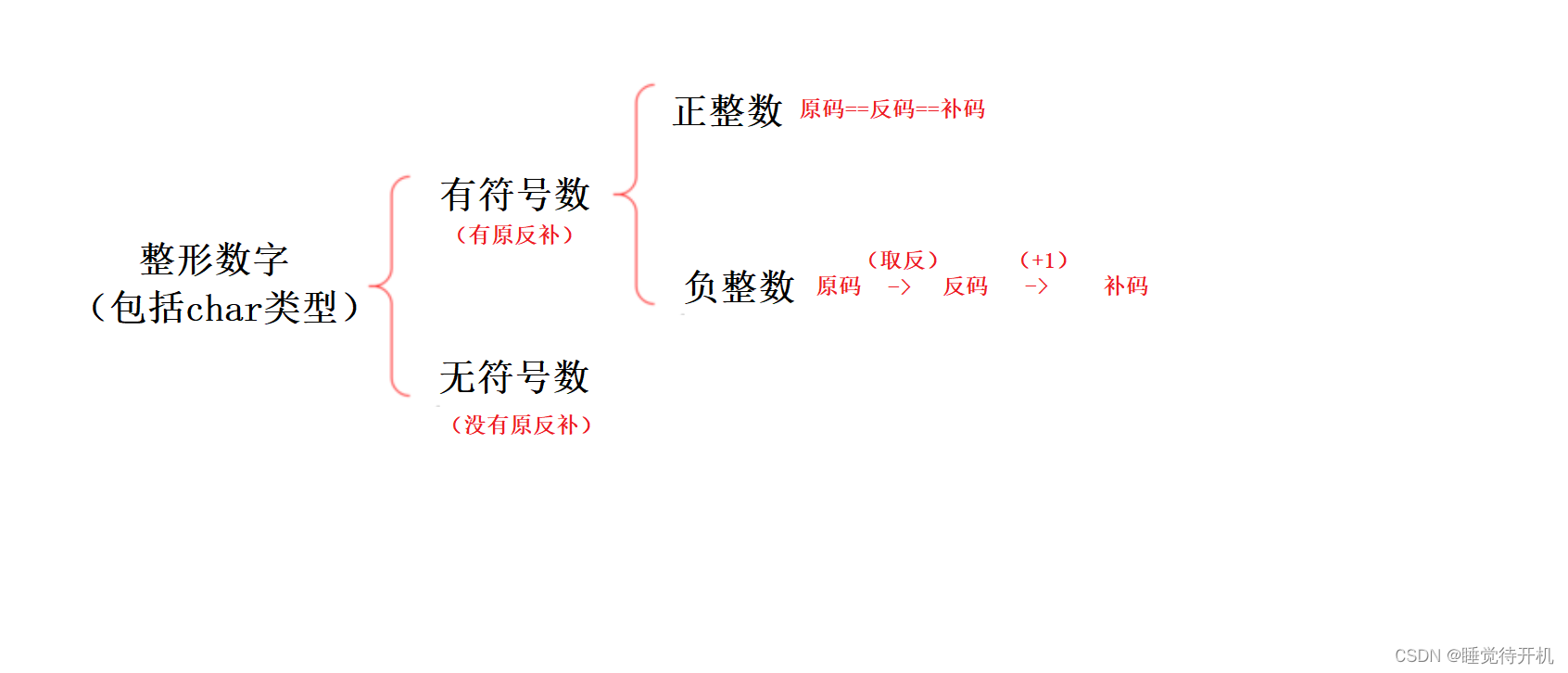
有符号数:
首先,对于有符号数,一定要能表示该数据是正数还是负数,所以我们一般用最高比特位来充当符号位。
原码反码补码都有符号位和数值位。符号位0表示正数,1表示负数,而三种表示方法各不相同。
无符号数:
不需要转换,原码反码补码相同不存在符号位。
如果一个数据是负整数,那么要遵守下面的规则进行转换:
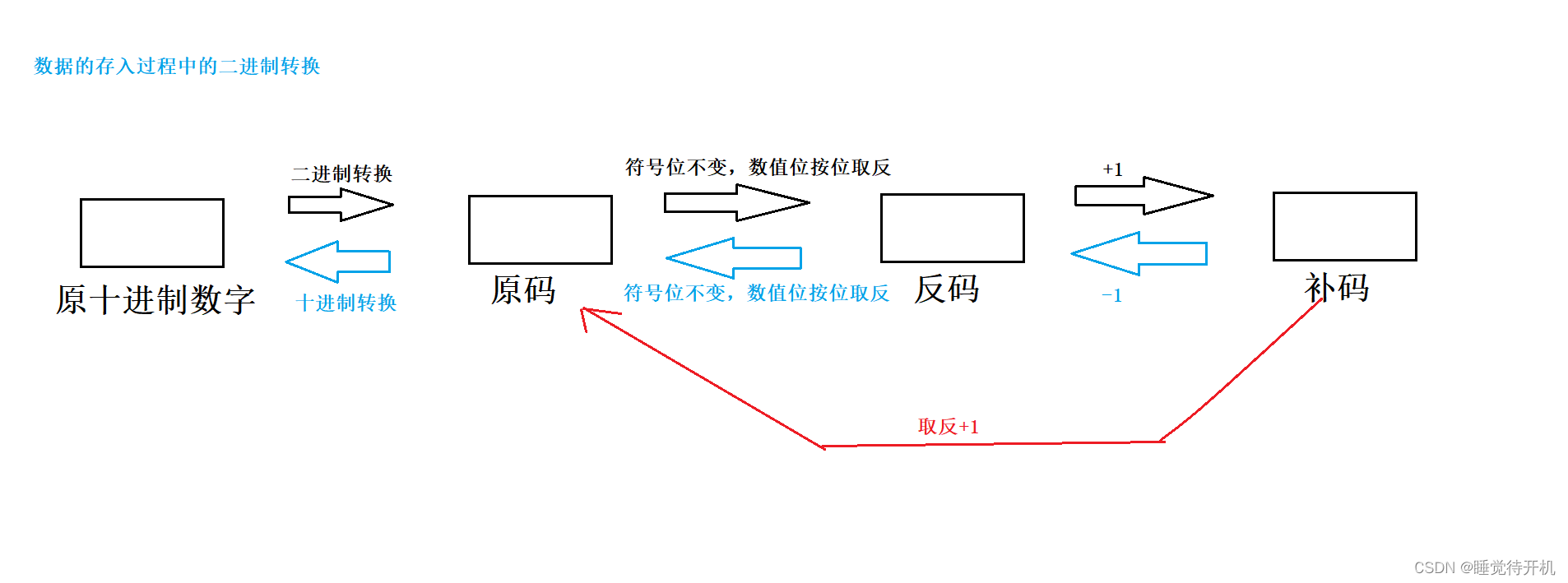
原码:直接将数字按照正负数的形式翻译成二进制即可
反码:符号位不变,数值位按位取反
补码:反码+1
无符号数:不需要转换(原码反码补码相同),没有符号位的概念
整形:数据存放内存中的其实是补码
为啥需要补码来存储整形类型?
原因在于:
1.使用补码,可以将符号位和数值位进行统一处理,并且加法和减法也可以统一进行处理
2.原码与补码的相互转换,其运算过程是相同的(都是取反+1),不需要格外的硬件电路
我需要强调一点的是,右边数字的二进制转换与左边的类型没有半毛钱关系,编译器判断有无符号整形,只看你赋值的数字有没有+号或者-号而已
那同学觉得计算机就这样把补码扔到内存了吗?
显然不只如此!还需要考虑大小端存储问题。
2.大小端存储
大小端存储取决于硬件单元,这个大小端存储是啥意思呢?
大小端存储的概念:
大端:低权值数字放到高地址处,高权重数字放到低地址处。
小端:低权值数字放到低地址处,高权值数字放到高地址处。

3.截断
考虑到怎么存储之后,我们还得需要考虑一个问题,就是会不会发生截断?比如你把一个数字放到一个char类型里面,char类型只有8个比特位,存不下一个数字的32个比特位,必然要发生截断。
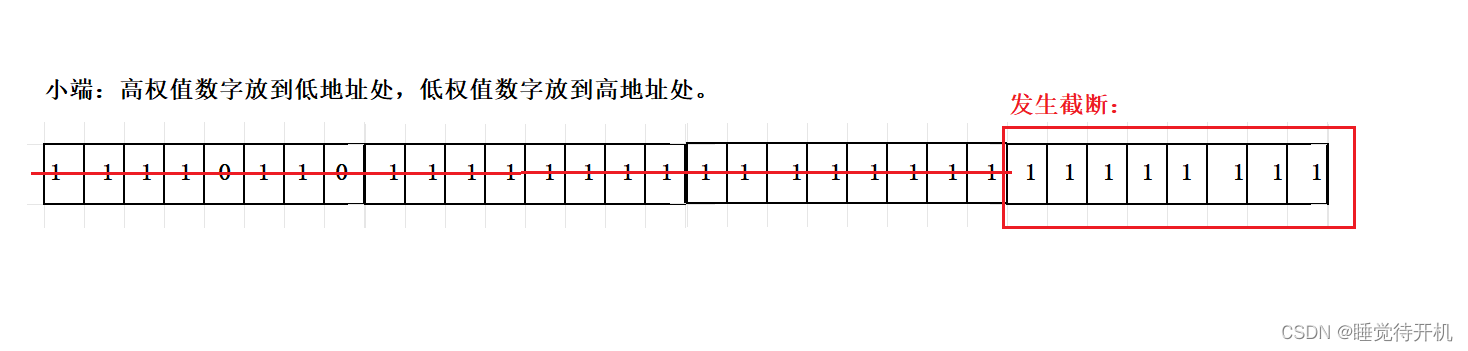
当然对于截断问题,只是顺便一提,有兴趣可以单独去研究一下。
4.取值范围的问题
一个类型有取值范围,那你知道取值范围是怎么进行确定的吗?
一个类型的取值范围的大小取决于这个类型有多少个比特位
假如我只给你一个比特位,请问你可以表示几个数字(不考虑符号位)?
就俩数字(2^1)嘛,一个0一个1嘛
我如果给你两个比特位呢?
4(2^2)个数字,00,01,10,11
我如果给你三个比特位呢?
8(2^3)个数字,000,001,010,011,100,101,110,111
……
所以,,,一个8个比特位的char类型,可以表示几个数字?2^8==256!
这也就解释char(有符号)类型的取值范围是-128—127了。
但是我有个小疑惑,-128靠8个比特位是怎么表示出来的?明明需要9个比特位啊。

只是人为规定!!!
之后呢,还要给大家看一个取值循环图,大家就能明白类型的取值范围是怎么回事了:
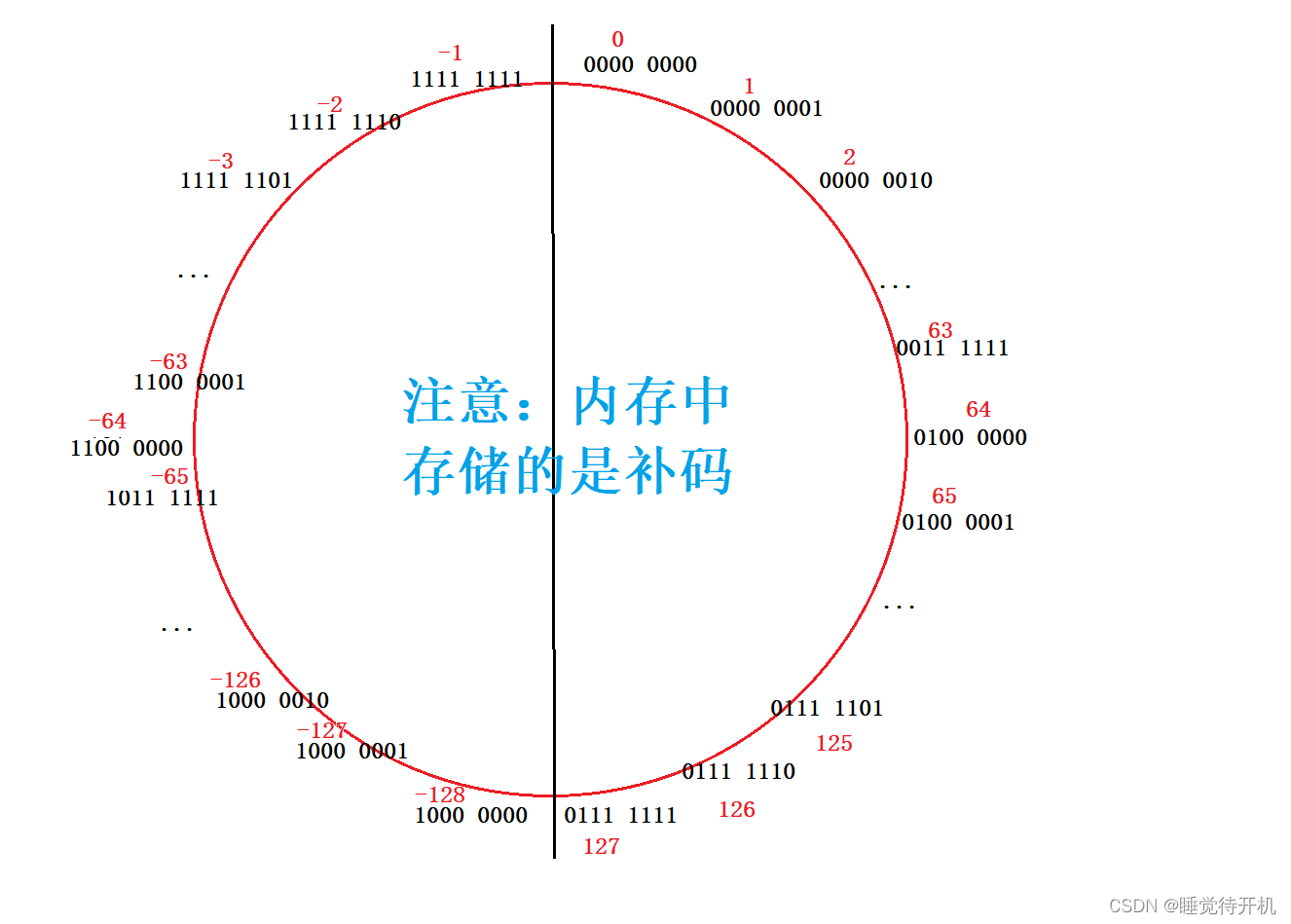
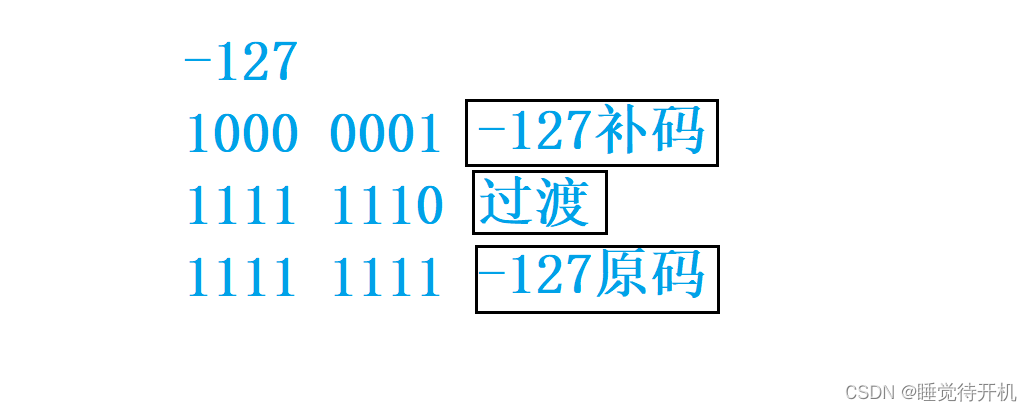
三、数据取出
1.大小端
还是要先看大小端问题,小端存储就小端取出,大端存储就大端取出即可。
2.自身类型
到了这个时候,说实在的左边的类型才有作用,什么意思呢?左边的类型决定了怎么看待这串二进制数字。
比如说左边如果是无符号整形类型,那么就不会把二进制最高位看成符号位,同理,如果是有符号类型,就会把最高位的二进制位看成符号位,这两种情况是截然不同的数值!

3.整型提升
如果我在内存里面是一个8个比特位的字符呢?你放入的类型却是一个int类型怎么办?整型提升。有符号int补符号位,无符号int前面补0,给你补到32个比特位再说。当然,这个地方也就不细说了,有兴趣可以自行研究一下。
练习题
最后送大家一道练习题哈,如果看完本文章大体理解我说的啥的话,应该可以做对,当然不对的话也不要担心哈,再弄懂就好啦,知识不是一下就会弄懂的。
int main()
{char a[1000];int i;for (i = 0; i < 1000; i++){a[i] = -1 - i;}printf("%d", strlen(a)); return 0;
}
答案:255,请试分析本题。
解析:略。
相关文章:

【C语言深度剖析——第四节(关键字4)】《C语言深度解剖》+蛋哥分析+个人理解
追求本质,不断进步 本文由睡觉待开机原创,转载请注明出处。 本内容在csdn网站首发 欢迎各位点赞—评论—收藏 如果存在不足之处请评论留言,共同进步! 这里写目录标题 一、空间的申请1.变量定义1.1变量定义的概念:1.2变…...

鸿蒙开发系列教程(五)--ArkTS语言:组件开发
1、基础组件 组件API文档:https://developer.huawei.com/consumer/cn/doc/harmonyos-references-V2/84_u58f0_u660e_u5f0f_u5f00_u53d1_u8303_u5f0f_uff09-0000001427744776-V2 查看组件API 外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传 容…...

Java:正则表达式讲解加举例,简洁易懂
正则表达式定义: 由一些特定的字符组成,代表的是一个规则。 作用:1.校验数据是否合法。2.可以在一段文本中查找满足要求的内容。 先自己写一个方法去校验qq号,比较与正则表达式的区别: 正则表达式的代码暂时可以不…...

2.机器学习-K最近邻(k-Nearest Neighbor,KNN)分类算法原理讲解
2️⃣机器学习-K最近邻(k-Nearest Neighbor,KNN)分类算法原理讲解 个人简介一算法概述二算法思想2.1 KNN的优缺点 三实例演示3.1电影分类3.2使用KNN算法预测 鸢(yuan)尾花 的种类3.3 预测年收入是否大于50K美元 个人简介 🏘️&…...
WordPress顶部管理工具栏怎么添加一二级自定义菜单?
默认情况下,WordPress前端和后台页面顶部都有一个“管理工具栏”,左侧一般就是站点名称、评论、新建,右侧就是您好,用户名称和头像。那么我们是否可以在这个管理工具栏中添加一些一二级自定义菜单呢? 其实,…...
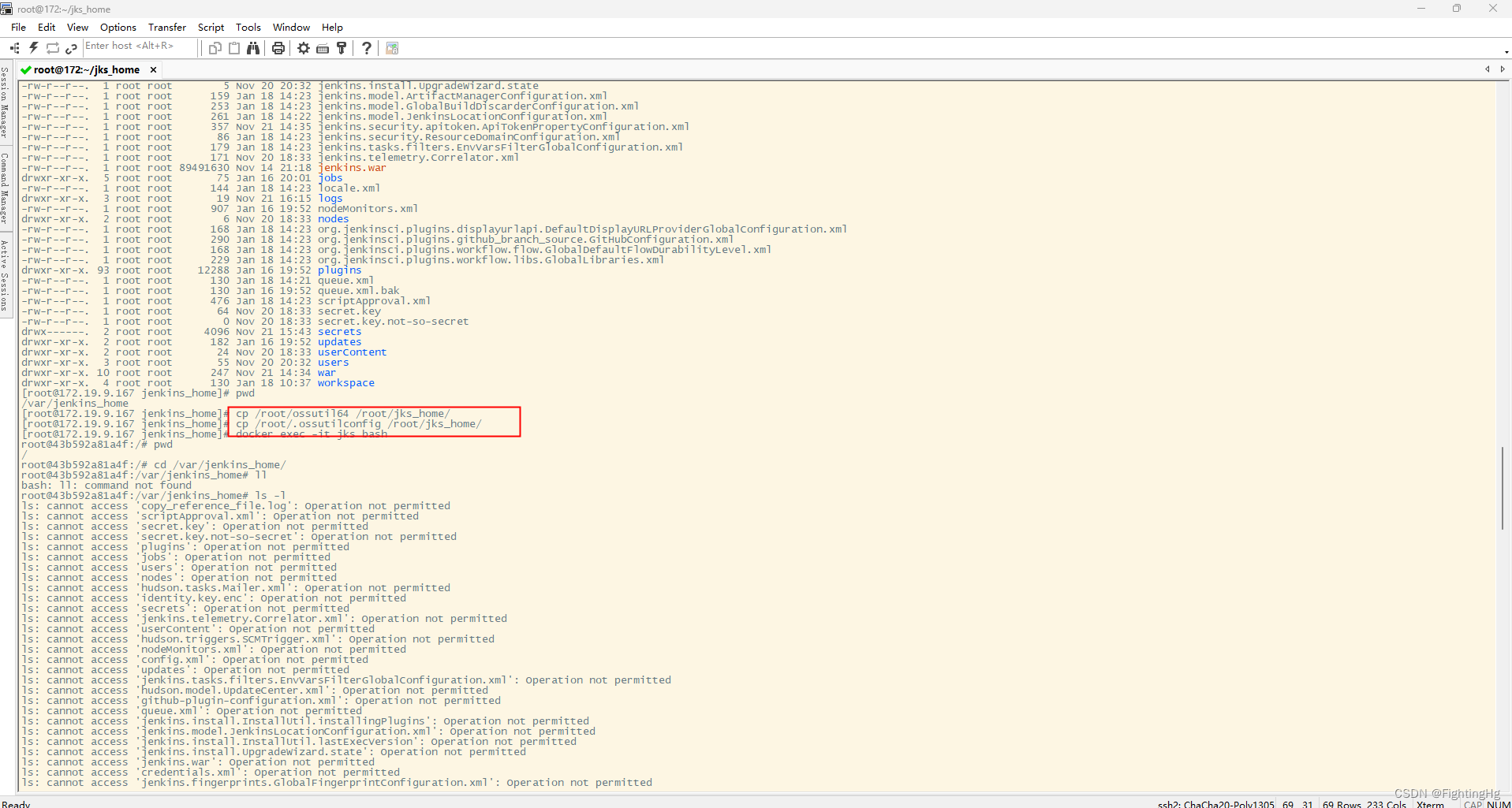
Linux安装ossutil工具且在Jenkins中执行shell脚本下载文件
测试中遇到想通过Jenkins下载OSS桶上的文件,要先在linux上安装ossutil工具,记录安装过程如下: 一、下载安装ossutil,使用命令 1.下载:wget https://gosspublic.alicdn.com/ossutil/1.7.13/ossutil64 2.一定要赋权限…...
Docker命令---搜索镜像
介绍 使用docker命令搜索镜像。 命令 docker search 镜像命令:版本号示例 以搜索ElasticSearch镜像为例 docker search ElasticSearch...
docker使用http_proxy配置代理
钢铁知识库,一个学习python爬虫、数据分析的知识库。人生苦短,快用python。 在内网服务器中,docker经常需要下载拉取镜像,但由于没有网络要么只能手动导入镜像包,又或者通过http_proxy代理到其它服务器下载。 解决方法…...
综述:自动驾驶中的 4D 毫米波雷达
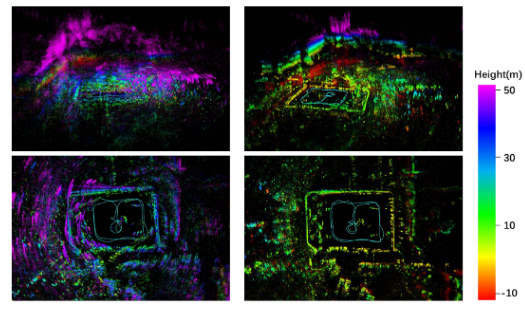
论文链接:《4D Millimeter-Wave Radar in Autonomous Driving: A Survey》 摘要 4D 毫米波 (mmWave) 雷达能够测量目标的距离、方位角、仰角和速度,引起了自动驾驶领域的极大兴趣。这归因于其在极端环境下的稳健性以及出色的速度和高度测量能力。 然而…...
)
蓝桥杯:1.特殊日期(Java)
题目描述 对于一个日期,我们可以计算出年份的各个数位上的数字之和,也可以分别计算月和日的各位数字之和。 请问从1900年1月1日至9999年12月31日,总共有多少天,年份的数位数字之和等于月的数位数字之和加日的数位数字之和。 例如&…...
服务异步通讯之 SpringAMQP【微服务】
文章目录 一、初识 MQ1. 同步通讯2. 异步通讯3. MQ 常见框架 二、RabbitMQ 入门1. 概述和安装2. 常见消息模型3. 基础模型练习 三、SpringAMQP1. 简单队列模型2. 工作队列模型3. 发布订阅模型3.1 Fanout Exchange3.2 Direct Exchange3.3 Topic Exchange 一、初识 MQ 1. 同步通…...

LED闪烁
这段代码是用于STM32F10x系列微控制器的程序,主要目的是初始化GPIOA的Pin 0并使其按照特定的模式进行闪烁。下面是对这段代码的逐行解释: #include "stm32f10x.h":这一行包含了STM32F10x系列微控制器的设备头文件。这个头文件包含…...
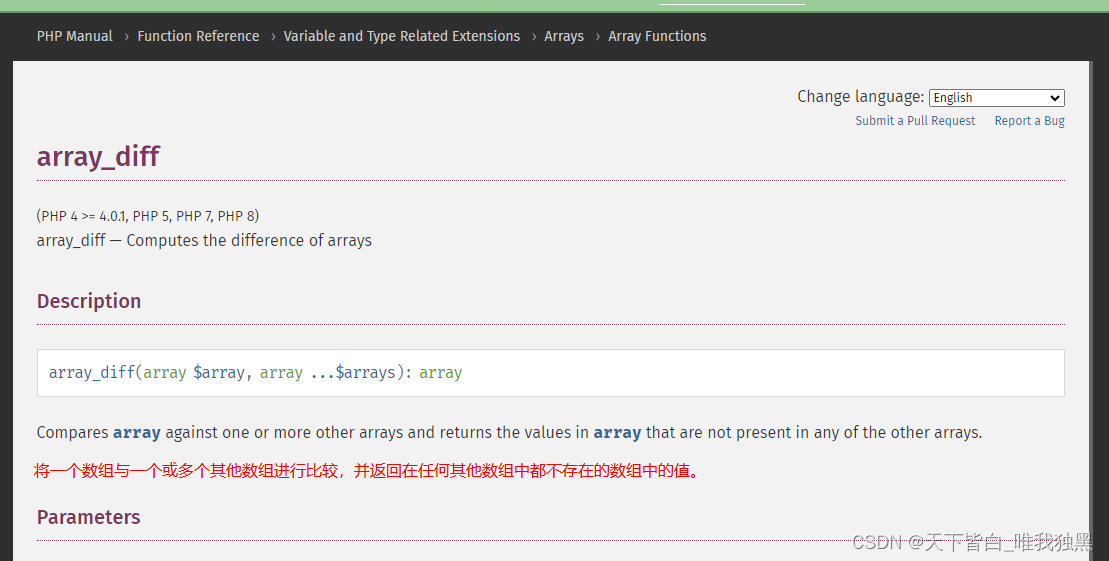
php array_diff 比较两个数组bug避坑 深入了解
今天实用array_diff出现的异常问题,预想的结果应该是返回 "integral_initiate">"0",实际没有 先看测试代码: $a ["user_name">"测","see_num">0,"integral_initiate&quo…...

c++中STL的vector简单实现
文章目录 vector构造函数 vector()拷贝构造 vector()析构函数 ~vector()iterator 的定义begin()与const版本end()与const版本增删改查尾插push_back()尾删pop_back()指定位置插入insert()指定位置删除 erase() operator[]与const版本容量增容reserve()设置容量 resize() 成员函…...

C# 更改Bitmap图像色彩模式
方法一:直接修改RGB的值 首先将BitmapData扫描线上的所有像素复制到字节数组中,然后遍历数组并对每个像素的RGB值进行修改,最后将修改后的像素值复制回BitmapData。这个过程不会影响原始的Bitmap对象,但会改变锁定的位图区域的数…...
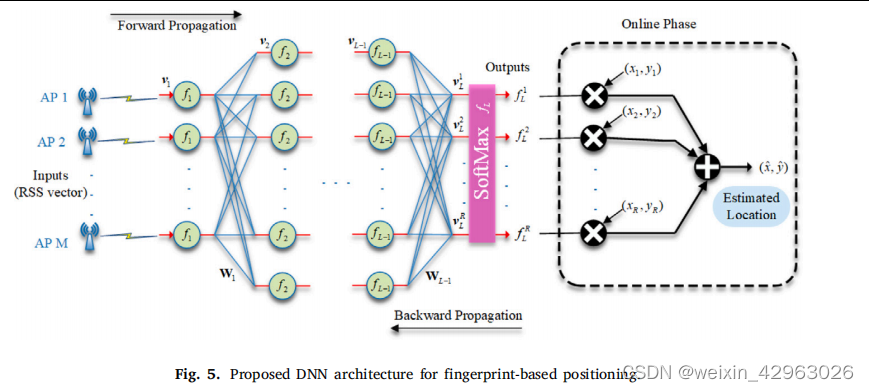
5.2 基于深度学习和先验状态的实时指纹室内定位
文献来源 Nabati M, Ghorashi S A. A real-time fingerprint-based indoor positioning using deep learning and preceding states[J]. Expert Systems with Applications, 2023, 213: 118889.(5.2_基于指纹的实时室内定位,使用深度学习和前一状态&…...

AIGC时代高效阅读论文实操
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...
对网站进行打点(不要有主动扫描行为)
什么是打点? 简单来说就是获取一个演习方服务器的控制权限。 目的: 1. 上传一个一句话木马 2. 挖到命令执行 3. 挖到反序列化漏洞 4. 钓鱼 假设对“千峰”网站进行打点: 1. 利用平台 1. 利用各类平台: 天眼查-商业查询平…...
)
502. IPO(贪心算法+优先队列/堆)
整体思想:在满足可用资金的情况下,选择其中利润最大的业务,直到选到k个业务为止,注意k可能比n大。 每次选择完一个业务,可用资金都会变动,这是可选择的业务也会变化,因此每次将可选择的业务放在…...

设计模式篇---中介者模式
文章目录 概念结构实例总结 概念 中介者模式:用一个中介对象来封装一系列的对象交互。中介者使各对象不需要显示地相互引用,从而使其耦合松散,而且可以独立地改变它们之间的交互。 就好比世界各个国家之间可能会产生冲突,但是当产…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
