【数据结构初阶】详解“树”
目录
前言
1.树概念及结构
(1)树的概念
(2)树的名词介绍
(3)树的表示
编辑 2.二叉树概念及结构
(1)概念
(2)特殊的二叉树
(3)二叉树的性质
(4)二叉树的存储结构
总结
前言
接下来077会使用几篇文章来讲解树的相关概念,以及树的实现,结构,如何使用树,希望可以帮助到大家。
1.树概念及结构
(1)树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。

如这幅图片就是一颗树,他的形状类似于我们在日常生活中所见到的树,只不过他的根在上边,叶子在下边,可以说是一颗逆置的树。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构

所以说除了根节点外,所有结点只有一个父节点才能成为树。
(2)树的名词介绍

节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;树的高度或深度:树中节点的最大层次; 如上图:树的高度为4堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙森林:由m(m>0)棵互不相交的树的集合称为森林;
(3)树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};就是用一个结构体,存储该结点的数据,并且存储这个结点的第一个孩子结点,以及这个结点的下一个兄弟结点,通过这样的结构就可以实现对所有结点的遍历。

例如在我们的日常的生活中,我们的文件目录就是一个树来实现的。
 2.二叉树概念及结构
2.二叉树概念及结构
(1)概念
一棵二叉树是结点的一个有限集合,该集合:1. 或者为空2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

我们需要注意的是二叉树中结点的最大度为2,即二叉树的度最大为2。二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
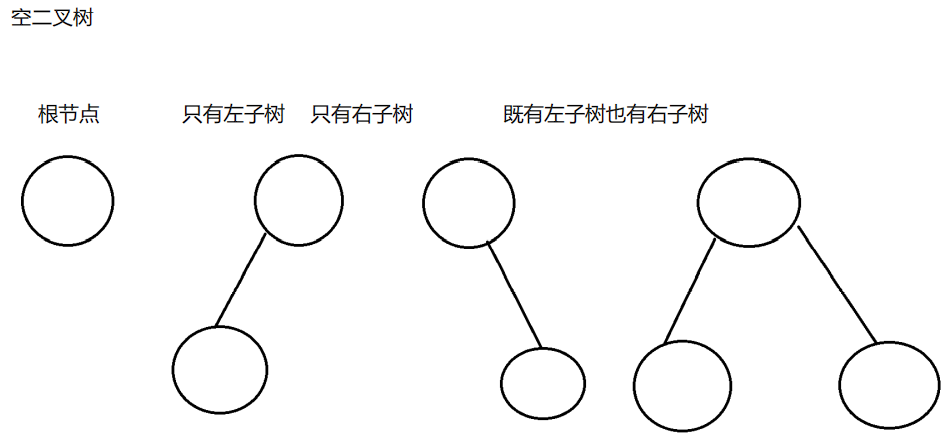
(2)特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是2^k-1,则它就是满二叉树。2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
完全二叉树的特点是叶子结点必须是连续的。

(3)二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1)个结点.2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-13. 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为 n2,则有 n0= n2+14. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1). (ps:h=log2(n+1) 是log以2为底,n+1为对数)5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对 于序号为i的结点有:1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
(4)二叉树的存储结构

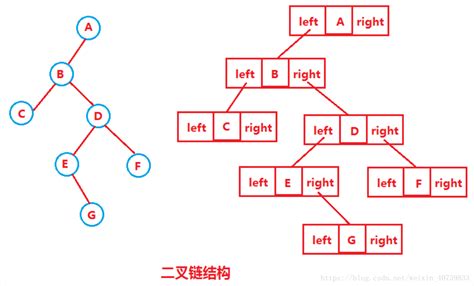
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};总结
这篇文章介绍了树与二叉树的相关概念,以及树和二叉树的结构,我们知道了二叉树可以链式存储和顺序存储,从下篇文章开始我们来实现二叉树的顺序存储。
相关文章:

【数据结构初阶】详解“树”
目录 前言 1.树概念及结构 (1)树的概念 (2)树的名词介绍 (3)树的表示 编辑 2.二叉树概念及结构 (1)概念 (2)特殊的二叉树 (3࿰…...

20230304 CF855 div3 vp
Dashboard - Codeforces Round 855 (Div. 3) - Codeforces呃呃,评价是,毫无进步呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训…...
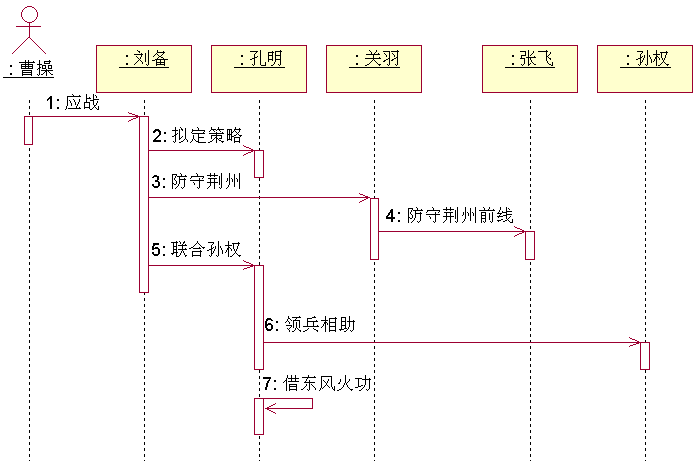
UML 时序图
时序图(Sequence Diagram)是显示对象之间交互的图,是按时间顺序排列的。 时序图中显示的是参与交互的对象及其对象之间消息交互的顺序。 时序图包括的建模元素主要有:对象(Actor)、生命线(Lif…...
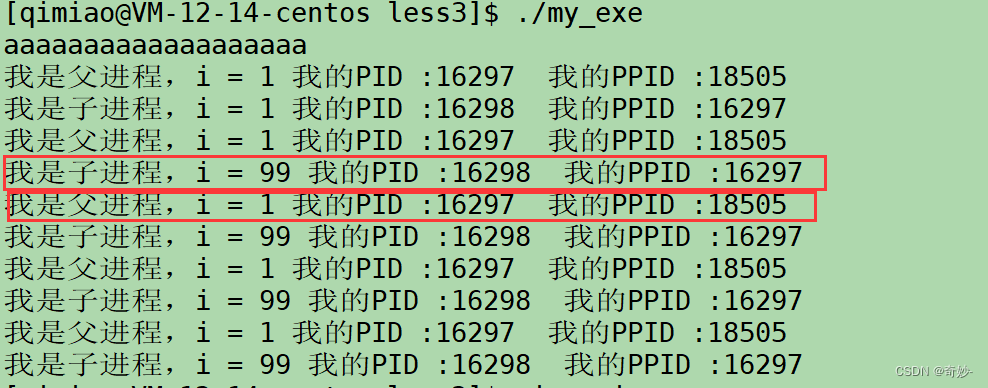
详解进程 及 探查进程
进程的概念PCB是什么task_struct的作用如何执行进程进程的探查什么是bashps命令的使用(查看进程)创建进程探究父子进程进程的概念 简而言之,进程就是正在在执行的程序 之前说过,程序执行的第一步Windows是双击程序Linux是 ./ &a…...
汇编相关问题
汇编语言期末复习题DX:单项选择题 DU:多项选择题 TK:填空题 MC:名词解释 v JD:简答题 CXFX:程序分析题 CXTK:程序填空题 BC:编程题第1章:基础知识1、在汇编语言程序的开发…...

华为OD机试Golang解题 - 火星文计算 2 | 包含思路
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

成功解决configure: error: the HTTP rewrite module requires the PCRE library
文章目录 前言问题复现问题解决思考环节总结前言 大家好,我是沐风晓月,本专栏是记录日常实验中的所有疑难杂症,教程的安装,程序的bug,甚至各类报错,如果你也遇到了困惑和问题,欢迎与我一起交流学习。 另外不要解决完问题就结束了,思考环节也要好好看看哦。 问题复现…...

UNIX--GDB调试
通常,在为调试而编译时,我们会关掉编译器优化选项(-O),并打开调试选项(-g)。另外,-Wall 在尽量不影响程序行为的情况下选项打开所有 warning,也可以发现许多问题,避免一些不必要的 BUG。 GDB 命令-启动、退…...

孤单数算法
1.背景 腾讯终面:孤单的QQ号码怎么找? 问题一:有n个QQ号码,除1个孤单的QQ号码外,其余的QQ号码都是成双成对的,求这个孤单的QQ号码,要求:时间复杂度为O(n), 空间复杂度为O(1). 问题…...

triangulate_object_model_3d算子总结
目录 1.去掉固定方向的点云干扰 2.增加八叉树深度,实现更高细节级别的三角测量 3.腐蚀和膨胀,得到更平滑的点云 1.去掉固定方向的点云干扰 例程:triangulate_object_model_3d_xyz_mapping.hdev...
ZincSearch Java 客户端教程
ZincSearch Zinc 简单、强大,不了解的同学可以参见我之前的博客。今天我们这里谈谈 Java 环境如何集成 Zinc 客户端,跟如何使用的。 安装 Zinc 到 Github 的官方 Releases 下载: 我的是 Windows 开发环境,下载 zincsearch_0.4…...
数据结构(一)(嵌入式学习)
数据结构干货总结(一)基础线性表的顺序表示线性表的链式表示单链表双链表循环链表循环单链表循环双链表栈顺序存储链式存储队列队列的定义队列的常见基本操作队列的顺序存储结构顺序队列循环队列队列的链式存储结构树概念二叉树二叉树的创建基础 数据&a…...

合成复用原则-快速理解
什么是合成/聚合复用原则? 合成/聚合复用原则是在一个新的对象里面使用一些已有的对象,使之成为新对象的一部分;新的对象通过向这些对象的委派达到复用已有功能的目的。 简述为:要尽量使用合成/聚合,尽量不要使用继承…...

Scala04 方法与函数
Scala04 方法与函数 Scala 中的也有方法和函数的概念。 Scala中的 方法 是类的一部分。 Scala中的 函数 是一个对象,可以赋值给变量。 在类中定义的函数就是方法 4.1 方法 Scala 中方法 与 Java 中类似,是组成类的一部分 4.1.1 语法结构 格式&#x…...
)
XJTUSE专业课与实验指南(已经开源)
文章目录XJTUSE专业课与实验指南大一小学期大二上课程实验大二下课程实验大二小学期大三上课程实验大三下课程实验XJTUSE专业课与实验指南 github地址:https://github.com/yijunquan-afk/XJTUSE-NOTES.git 📄写在前面 1️⃣ 本篇文章仅供参考࿰…...
Spring面试专题
讲师:邓澎波 Spring面试专题 1.Spring应该很熟悉吧?来介绍下你的Spring的理解 1.1 Spring的发展历程 先介绍Spring是怎么来的,发展中有哪些核心的节点,当前的最新版本是什么等 通过上图可以比较清晰的看到Spring的各个时间版本…...

【truncate、delete和drop的6大区别!】
在MySQL中,truncate、delete和drop是三个常用的命令,它们可以用于删除表或表中的数据,下面是它们的六大区别: 语法不同: truncate和delete是SQL语句,drop是DDL(数据定义语言)语句。…...

如何入门Vue:掌握Vue的核心概念和基本用法
Vue是一种流行的JavaScript框架,它可以让开发者更容易地构建响应式的用户界面。Vue的设计理念是简单易懂,它的核心库只关注视图层,可以与其它库或现有项目很好地结合。在本文中,我将介绍Vue的基础概念和如何开始使用Vue。Vue的基本…...

APM飞控使用动捕等外部定位
本文初次写于2023.03.03,pixhawk飞控应该是刷写了ArduPilot 4.1以上的版本。 机载计算机通过WIFI和vrpn_ros_client获取动捕系统(vicon或者nokov)的无人机定位数据(x,y,z四元数),然…...
【vulhub漏洞复现】CVE-2013-4547 Nginx 文件名逻辑漏洞
一、漏洞详情影响版本 Nginx 0.8.41 ~ 1.4.3 / 1.5.0 ~ 1.5.7通过%00截断绕过后缀名的限制,使上传的php内容文件被解析执行。当Nginx得到一个用户请求时,首先对url进行解析,进行正则匹配,如果匹配到以.php后缀结尾的文件名&#x…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
