(蓝桥真题)最长不下降子序列(权值线段树)

样例输入:
5 1
1 4 2 8 5样例输出:
4分析:看到这种对其中连续k个数进行修改的我们就应该想到答案是由三部分组成,因为求的是最长不下降子序列,那么我们可以找到一个最合适的断点i,使得答案是由区间[1,i],[i+1,i+k],[i+k+1,n]三部分组成,其中区间[i+1,i+k]里面的数是可以任意变化的,那么我们只要在区间[1,i]和区间[i+k+1,n]中找到一个最长不下降子序列b1,b2,……,bm,那么我们就可以将区间[i+1,i+k]中的所有数变为某个bj,使得最长不下降子序列的长度为m+k,所以现在我们的关键问题就是为了求取m。
一般这种问题就是要设置一个前缀和一个后缀,表示含义如下:
f1[i]表示a[1~i]中以a[i]结尾的最长不下降子序列的长度
f2[i]表示a[i~n]中以a[i]开头的最长不下降子序列的长度
这两个数组显然可以用权值线段树预处理出来:
f1[i]:就是每次在加入a[i]之前,先看一下线段树中以小于等于a[i]的值结尾的最长不下降子序列的长度的最大值,然后在这个基础上+1即可得到
f2[i]:这个要从后往前遍历,这个是在每次加入a[i]之前,先看一下线段树中以大于等于a[i]的值开头的最长不下降子序列的长度的最大值,然后在这个基础上+1即可得到
注意当求出这个值后要用f数组对权值线段树进行更新
那么我们枚举前半段区间的最长不下降子序列端点i,那么也就代表最长不下降子序列是由a[1~i]中的一部分和[i+1~i+k]中的全部以及a[i+k+1,n]中的一部分组成,由于我们枚举的前半段区间的最长不下降子序列的末尾,那么我们就要在区间[i+k+1,n]中找到以大于等于a[i]的值开头的最长不下降子序列的长度最大值,这个直接在求解f2[]过程中刚好可以利用权值线段树得到。
答案还有可能就是只有两段区间,这个要分两种情况,一种是只有a[1~i]中的一部分和[i+1~i+k]中的全部,或者是只有[i+1~i+k]中的全部以及a[i+k+1,n]中的一部分组成,这两种情况直接用for循环遍历一遍即可得到,无非就是一种只用到f1[],另一种只用到f2[]。
细节见代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=5e5+10;
int l[N],r[N],mx[N];
int a[N];
int f1[N],f2[N];
/*
f1[i]表示a[1~i]中以a[i]结尾的最长不下降子序列的长度
f2[i]表示a[i~n]中以a[i]开头的最长不下降子序列的长度
*/
vector<int>alls;
int find(int x)
{return lower_bound(alls.begin(),alls.end(),x)-alls.begin()+1;
}
void pushup(int id)
{mx[id]=max(mx[id<<1],mx[id<<1|1]);
}
void build(int id,int L,int R)
{l[id]=L;r[id]=R;mx[id]=0;if(L==R) return ;int mid=L+R>>1;build(id<<1,L,mid);build(id<<1|1,mid+1,R);pushup(id);
}
void update_point(int id,int pos,int val)
{if(l[id]==r[id]){mx[id]=val;return ;}int mid=l[id]+r[id]>>1;if(pos<=mid) update_point(id<<1,pos,val);else update_point(id<<1|1,pos,val);pushup(id);
}
int query_interval(int id,int L,int R)
{if(l[id]>=L&&r[id]<=R) return mx[id];int mid=l[id]+r[id]>>1;int ans=0;if(L<=mid) ans=max(ans,query_interval(id<<1,L,R));if(mid+1<=R) ans=max(ans,query_interval(id<<1|1,L,R));return ans;
}
int main()
{int n,k;cin>>n>>k;for(int i=1;i<=n;i++){scanf("%d",&a[i]);alls.push_back(a[i]); }sort(alls.begin(),alls.end());alls.erase(unique(alls.begin(),alls.end()),alls.end());for(int i=1;i<=n;i++)a[i]=find(a[i]);build(1,1,alls.size());for(int i=1;i<=n;i++){f1[i]=query_interval(1,1,a[i])+1;update_point(1,a[i],f1[i]);}int ans=0;build(1,1,alls.size());for(int i=n;i>=1;i--){f2[i]=query_interval(1,a[i],alls.size())+1;update_point(1,a[i],f2[i]);if(i>k){ans=max(ans,f1[i-k-1]+k+query_interval(1,a[i-k-1],alls.size()));ans=max(ans,k+f2[i]);}if(i+k<=n) ans=max(ans,k+f1[i]);}printf("%d\n",ans);return 0;
} 相关文章:

(蓝桥真题)最长不下降子序列(权值线段树)
样例输入: 5 1 1 4 2 8 5 样例输出: 4 分析:看到这种对其中连续k个数进行修改的我们就应该想到答案是由三部分组成,因为求的是最长不下降子序列,那么我们可以找到一个最合适的断点i,使得答案是由区间[1…...

数据类型及参数传递
1.数据类型 java中的基本数据类型: 数值型: 整数型:byte short long int 浮点型:float double 布尔型: boolean字符串: char java中的引用数据类型: 数组(array) 类(class…...

永春堂1300系统开发|解析永春堂1300模式商城的五大奖项
电商平台竞争越来越激烈,各种营销方式也是层出不穷,其中永春堂1300营销模式,以其无泡沫和自驱动性强等特点风靡一时。在这套模式中,虽然单型价格差异较大,但各种奖励的设计,巧妙的兼顾了平台和所有会员的利…...

最近一年我都干了什么——反思!!
过去一年不管是学习方式还是心态上都和以往有了许多不同的地方,比较昏昏沉沉。最近慢慢找到状态了,就想赶紧记录下来。 学习 在学习新技术的过程中开始飘了,总感觉有了一些开发经验后就觉得什么都不用记,知道思路就行遇到了现场百…...
save 和 export 命令的区别)
Docker学习(十七)save 和 export 命令的区别
Docker 中有两个命令可以将镜像导出为本地文件系统中的 tar 文件:docker save 和 docker export。尽管它们的作用类似,但它们之间有一个重要的区别。 1.使用方式的不同: docker save 的使用示例: docker save -o test.tar image…...
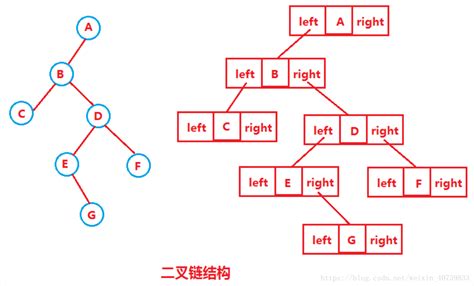
【数据结构初阶】详解“树”
目录 前言 1.树概念及结构 (1)树的概念 (2)树的名词介绍 (3)树的表示 编辑 2.二叉树概念及结构 (1)概念 (2)特殊的二叉树 (3࿰…...

20230304 CF855 div3 vp
Dashboard - Codeforces Round 855 (Div. 3) - Codeforces呃呃,评价是,毫无进步呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训了该加训…...
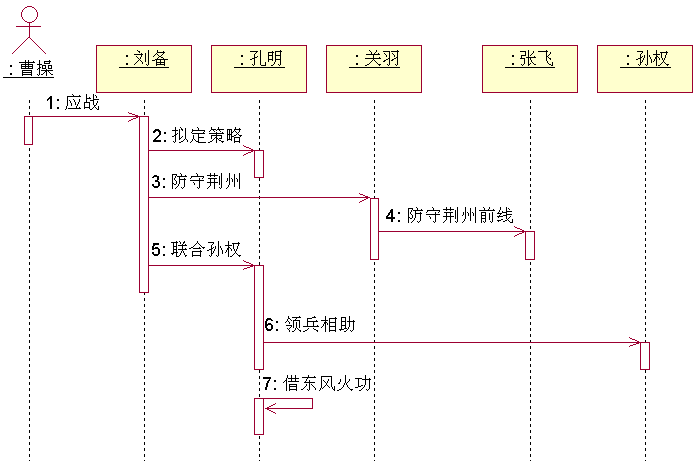
UML 时序图
时序图(Sequence Diagram)是显示对象之间交互的图,是按时间顺序排列的。 时序图中显示的是参与交互的对象及其对象之间消息交互的顺序。 时序图包括的建模元素主要有:对象(Actor)、生命线(Lif…...
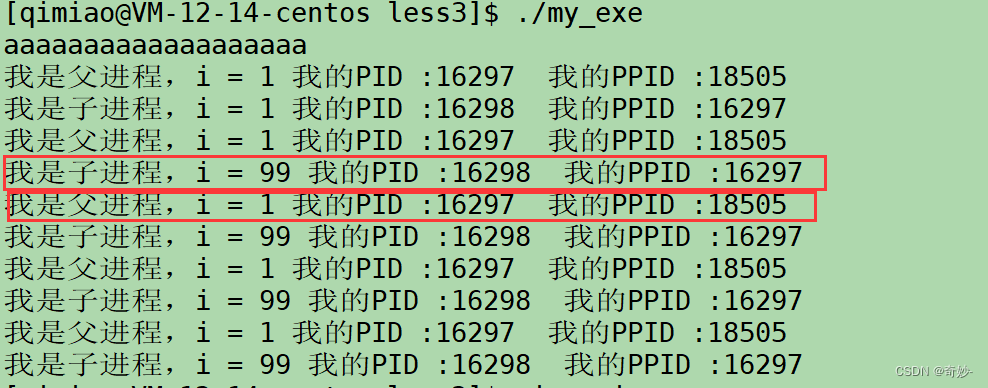
详解进程 及 探查进程
进程的概念PCB是什么task_struct的作用如何执行进程进程的探查什么是bashps命令的使用(查看进程)创建进程探究父子进程进程的概念 简而言之,进程就是正在在执行的程序 之前说过,程序执行的第一步Windows是双击程序Linux是 ./ &a…...
汇编相关问题
汇编语言期末复习题DX:单项选择题 DU:多项选择题 TK:填空题 MC:名词解释 v JD:简答题 CXFX:程序分析题 CXTK:程序填空题 BC:编程题第1章:基础知识1、在汇编语言程序的开发…...

华为OD机试Golang解题 - 火星文计算 2 | 包含思路
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

成功解决configure: error: the HTTP rewrite module requires the PCRE library
文章目录 前言问题复现问题解决思考环节总结前言 大家好,我是沐风晓月,本专栏是记录日常实验中的所有疑难杂症,教程的安装,程序的bug,甚至各类报错,如果你也遇到了困惑和问题,欢迎与我一起交流学习。 另外不要解决完问题就结束了,思考环节也要好好看看哦。 问题复现…...

UNIX--GDB调试
通常,在为调试而编译时,我们会关掉编译器优化选项(-O),并打开调试选项(-g)。另外,-Wall 在尽量不影响程序行为的情况下选项打开所有 warning,也可以发现许多问题,避免一些不必要的 BUG。 GDB 命令-启动、退…...

孤单数算法
1.背景 腾讯终面:孤单的QQ号码怎么找? 问题一:有n个QQ号码,除1个孤单的QQ号码外,其余的QQ号码都是成双成对的,求这个孤单的QQ号码,要求:时间复杂度为O(n), 空间复杂度为O(1). 问题…...

triangulate_object_model_3d算子总结
目录 1.去掉固定方向的点云干扰 2.增加八叉树深度,实现更高细节级别的三角测量 3.腐蚀和膨胀,得到更平滑的点云 1.去掉固定方向的点云干扰 例程:triangulate_object_model_3d_xyz_mapping.hdev...
ZincSearch Java 客户端教程
ZincSearch Zinc 简单、强大,不了解的同学可以参见我之前的博客。今天我们这里谈谈 Java 环境如何集成 Zinc 客户端,跟如何使用的。 安装 Zinc 到 Github 的官方 Releases 下载: 我的是 Windows 开发环境,下载 zincsearch_0.4…...
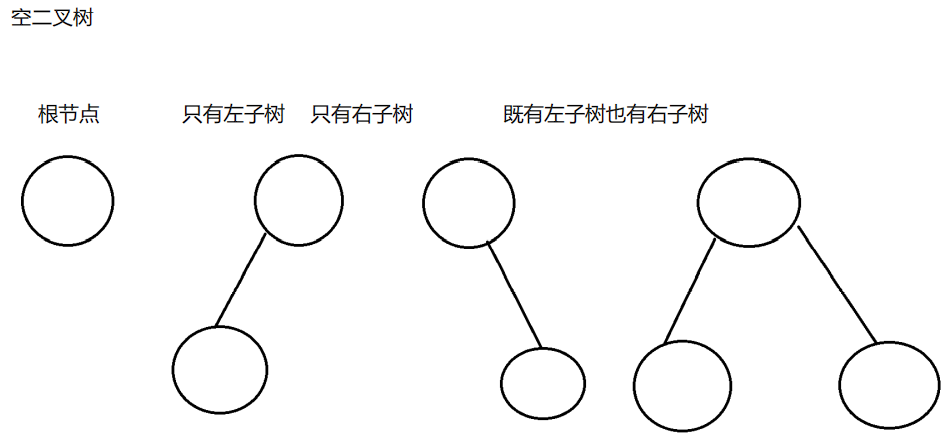
数据结构(一)(嵌入式学习)
数据结构干货总结(一)基础线性表的顺序表示线性表的链式表示单链表双链表循环链表循环单链表循环双链表栈顺序存储链式存储队列队列的定义队列的常见基本操作队列的顺序存储结构顺序队列循环队列队列的链式存储结构树概念二叉树二叉树的创建基础 数据&a…...

合成复用原则-快速理解
什么是合成/聚合复用原则? 合成/聚合复用原则是在一个新的对象里面使用一些已有的对象,使之成为新对象的一部分;新的对象通过向这些对象的委派达到复用已有功能的目的。 简述为:要尽量使用合成/聚合,尽量不要使用继承…...

Scala04 方法与函数
Scala04 方法与函数 Scala 中的也有方法和函数的概念。 Scala中的 方法 是类的一部分。 Scala中的 函数 是一个对象,可以赋值给变量。 在类中定义的函数就是方法 4.1 方法 Scala 中方法 与 Java 中类似,是组成类的一部分 4.1.1 语法结构 格式&#x…...
)
XJTUSE专业课与实验指南(已经开源)
文章目录XJTUSE专业课与实验指南大一小学期大二上课程实验大二下课程实验大二小学期大三上课程实验大三下课程实验XJTUSE专业课与实验指南 github地址:https://github.com/yijunquan-afk/XJTUSE-NOTES.git 📄写在前面 1️⃣ 本篇文章仅供参考࿰…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
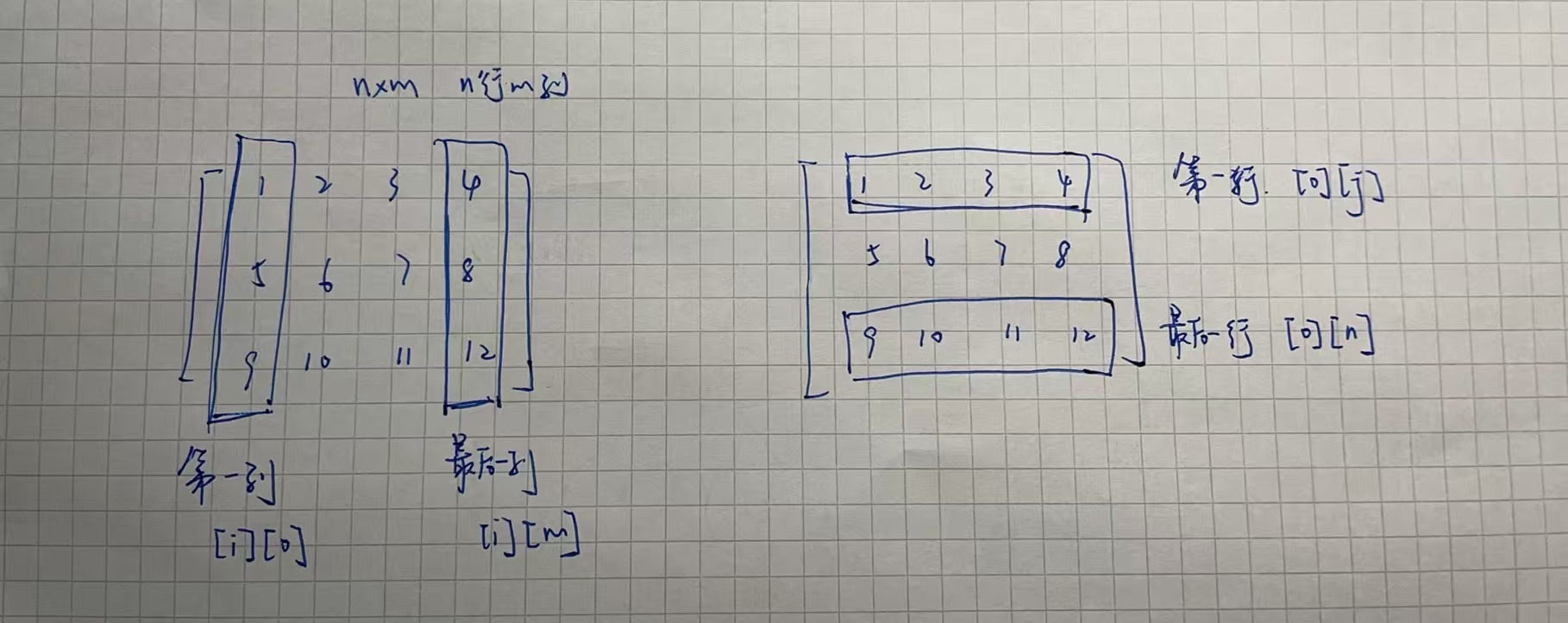
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...
