C++参悟：数值运算相关
数值运算相关
- 一、概述
- 二、常用数学函数
- 1. 基础运算
- 1. 浮点值的绝对值（ |x| ）
- 2. 浮点除法运算的余数
- 3. 除法运算的有符号余数
- 4. 除法运算的有符号余数和最后三个二进制位
- 5. 混合的乘加运算
- 6. 两个浮点值的较大者
- 7. 两个浮点值的较小者
- 8. 两个浮点值的正数差（ max(0, x-y) ）
- 2. 指数函数
- 1. 返回 e 的给定次幂（ e^x^ ）
- 2. 返回 2 的给定次幂（ 2^x^ ）
- 3. 返回 e 的给定次幂减一（ e^x^-1 ）
- 4. 自然（以 e 为底）对数（ ln(x) ）
- 5. 常用（以 10 为底）对数（ log~10~(x) ）
- 6. 给定数值的以 2 为底的对数（ log~2~(x) ）
- 7. 加上给定数值的自然（以 e 为底）对数（ ln(1+x) ）
- 3. 幂函数
- 1. 求某数的给定次幂（ x^y^ ）
- 2. 计算平方根（ √x ）
- 3. 计算立方根（ 3√x ）
- 4. 计算两个给定数的平方和的平方根（ √x^2^+y^2^ ）
- 4. 三角函数
- 1. 计算正弦（ sin(x) ）
- 2. 计算余弦（ cos(x) ）
- 3. 计算正切（ tan(x) ）
- 4. 计算反正弦（ arcsin(x) ）
- 5. 计算反余弦（ arccos(x) ）
- 6. 计算反正切（ arctan(x) ）
- 7. 反正切，用符号确定象限
- 5. 双曲函数
- 1. 计算双曲正弦（ sinh(x) ）
- 2. 计算双曲余弦（ cosh(x) ）
- 3. 计算双曲正切（ tanh(x) ）
- 4. 计算反双曲正弦（ arsinh(x) ）
- 5. 计算反双曲余弦（ arcosh(x) ）
- 6. 计算反双曲正切（ artanh(x) ）
- 6. 误差与伽马函数
- 1. 误差函数
- 2. 补误差函数
- 3. gamma 函数
- 4. gamma 函数的自然对数
- 7. 最接近整数的浮点运算
- 1. 不小于给定值的最接近整数值
- 2. 不大于给定值的最接近整数
- 3. 绝对值不大于给定值的最接近整数
- 4. 最接近整数，中间情况下向远离零舍入
- 5. 使用当前舍入模式的最接近整数
- 6. 使用当前舍入模式的最接近整数
- 8. 浮点操作函数
- 9. 分类与比较
- 三、宏常量
- 四、错误处理
一、概述
C++为我们提供了很多已经定义好的一些数学函数，这些函数的使用一定要注意函数的定义域，因为计算机表示的数据有限，有些非法的运算的结果也是在数值运算库中定义好了的。
二、常用数学函数
在标准库中基本上提供了对于 float、double、long double 类型参数的输入、也有对应的参数 float、double、long double 的输出。就像下面的可以看得出来 不带 任何的后缀是有3个类型的重载、带 ‘f’ 的指定了强制 float 类型、带 ‘l’ 的强制指定了 long double 类型。基本上下面提到的函数都会有这些后缀以满足不同精度的需求。
float fmod ( float x, float y );
double fmod ( double x, double y );
long double fmod ( long double x, long double y ); float fmodf( float x, float y );
long double fmodl( long double x, long double y );
1. 基础运算
1. 浮点值的绝对值（ |x| ）
基础定义： 就是求一个数值的绝对值
double abs( double arg );
abs(float x)
fabs
fabsf
fabsl
此函数不受制于任何指定于 math_errhandling 的错误条件。
若实现支持 IEEE 浮点算术（ IEC 60559 ），则
- 若输入参数为 ±0 ，则返回 +0
- 若输入参数为 ±∞ ，则返回 +∞
- 若输入参数为 NaN ，则返回 NaN
示例：
#include <iostream>
#include <cmath>int main()
{std::cout << "abs(+3.0) = " << std::abs(+3.0) << '\n'<< "abs(-3.0) = " << std::abs(-3.0) << '\n';// 特殊值std::cout << "abs(-0.0) = " << std::abs(-0.0) << '\n'<< "abs(-Inf) = " << std::abs(-INFINITY) << '\n'<< "abs(-NaN) = " << std::abs(-NAN) << '\n';
}
//输出
abs(+3.0) = 3
abs(-3.0) = 3
abs(-0.0) = 0
abs(-Inf) = inf
abs(-NaN) = nan
2. 浮点除法运算的余数
基础定义：计算除法运算 x/y 的浮点余数。有点像整数的余数运算符 %
double fmod ( double x, double y );
fmod
fmodf
fmodl
#include <iostream>
#include <cmath>
#include <cfenv>#pragma STDC FENV_ACCESS ON
int main()
{std::cout << "fmod(+5.1, +3.0) = " << std::fmod(5.1,3) << '\n'<< "fmod(-5.1, +3.0) = " << std::fmod(-5.1,3) << '\n'<< "fmod(+5.1, -3.0) = " << std::fmod(5.1,-3) << '\n'<< "fmod(-5.1, -3.0) = " << std::fmod(-5.1,-3) << '\n';// 特殊值std::cout << "fmod(+0.0, 1.0) = " << std::fmod(0, 1) << '\n'<< "fmod(-0.0, 1.0) = " << std::fmod(-0.0, 1) << '\n'<< "fmod(5.1, Inf) = " << std::fmod(5.1, INFINITY) << '\n';// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "fmod(+5.1, 0) = " << std::fmod(5.1, 0) << '\n';if(std::fetestexcept(FE_INVALID))std::cout << " FE_INVALID raised\n";
}
// 输出
fmod(+5.1, +3.0) = 2.1
fmod(-5.1, +3.0) = -2.1
fmod(+5.1, -3.0) = 2.1
fmod(-5.1, -3.0) = -2.1
fmod(+0.0, 1.0) = 0
fmod(-0.0, 1.0) = -0
fmod(5.1, Inf) = 5.1
fmod(+5.1, 0) = -nanFE_INVALID raised
3. 除法运算的有符号余数
基础定义：此函数所计算的除法运算 x/y 的 IEEE 浮点余数，准确地为值 x - n*y ，其中值 n 是最接近 x/y 准确值的整数值。 |n-x/y| = ½ 时，选择作为偶数的 n 。与 std::fmod() 相反，不保证返回值拥有与 x 相同的符号。若返回值是 0 ，则它拥有与 x 相同的符号。
double remainder ( double x, double y );
remainder
remainderf
remainderl
#include <iostream>
#include <cmath>
#include <cfenv>#pragma STDC FENV_ACCESS ON
int main()
{std::cout << "remainder(+5.1, +3.0) = " << std::remainder(5.1,3) << '\n'<< "remainder(-5.1, +3.0) = " << std::remainder(-5.1,3) << '\n'<< "remainder(+5.1, -3.0) = " << std::remainder(5.1,-3) << '\n'<< "remainder(-5.1, -3.0) = " << std::remainder(-5.1,-3) << '\n';// 特殊值std::cout << "remainder(-0.0, 1.0) = " << std::remainder(-0.0, 1) << '\n'<< "remainder(5.1, Inf) = " << std::remainder(5.1, INFINITY) << '\n';// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "remainder(+5.1, 0) = " << std::remainder(5.1, 0) << '\n';if(fetestexcept(FE_INVALID))std::cout << " FE_INVALID raised\n";
}
//输出
remainder(+5.1, +3.0) = -0.9
remainder(-5.1, +3.0) = 0.9
remainder(+5.1, -3.0) = -0.9
remainder(-5.1, -3.0) = 0.9
remainder(-0.0, 1.0) = -0
remainder(5.1, Inf) = 5.1
remainder(+5.1, 0) = -nanFE_INVALID raised
4. 除法运算的有符号余数和最后三个二进制位
基础定义：
remquo
remquof
remquol
5. 混合的乘加运算
基础定义：计算 (x*y) + z ，如同用无限精度，而仅舍入一次到结果类型。
double fma ( double x, double y, double z );
fma
fmaf
fmal
#include <iostream>
#include <iomanip>
#include <cmath>
#include <cfenv>
#pragma STDC FENV_ACCESS ON
int main()
{// 演示 fma 与内建运算符间的差别double in = 0.1;std::cout << "0.1 double is " << std::setprecision(23) << in<< " (" << std::hexfloat << in << std::defaultfloat << ")\n"<< "0.1*10 is 1.0000000000000000555112 (0x8.0000000000002p-3), "<< "or 1.0 if rounded to double\n";double expr_result = 0.1 * 10 - 1;double fma_result = fma(0.1, 10, -1);std::cout << "0.1 * 10 - 1 = " << expr_result<< " : 1 subtracted after intermediate rounding\n"<< "fma(0.1, 10, -1) = " << std::setprecision(6) << fma_result << " ("<< std::hexfloat << fma_result << std::defaultfloat << ")\n\n";// fma 用于 double-double 算术double high = 0.1 * 10;double low = fma(0.1, 10, -high);std::cout << "in double-double arithmetic, 0.1 * 10 is representable as "<< high << " + " << low << "\n\n";// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "fma(+Inf, 10, -Inf) = " << std::fma(INFINITY, 10, -INFINITY) << '\n';if(std::fetestexcept(FE_INVALID))std::cout << " FE_INVALID raised\n";
}
//输出
0.1 double is 0.10000000000000000555112 (0x1.999999999999ap-4)
0.1*10 is 1.0000000000000000555112 (0x8.0000000000002p-3), or 1.0 if rounded to double
0.1 * 10 - 1 = 0 : 1 subtracted after intermediate rounding
fma(0.1, 10, -1) = 5.55112e-17 (0x1p-54)in double-double arithmetic, 0.1 * 10 is representable as 1 + 5.55112e-17fma(+Inf, 10, -Inf) = -nanFE_INVALID raised
6. 两个浮点值的较大者
基础定义：返回二个浮点数的较大者
double fmax ( double x, double y );
fmax
fmaxf
fmaxl
#include <iostream>
#include <cmath>int main()
{std::cout << "fmax(2,1) = " << std::fmax(2,1) << '\n'<< "fmax(-Inf,0) = " << std::fmax(-INFINITY,0) << '\n'<< "fmax(NaN,-1) = " << std::fmax(NAN,-1) << '\n';
}
//输出：
fmax(2,1) = 2
fmax(-Inf,0) = 0
fmax(NaN,-1) = -1
7. 两个浮点值的较小者
基础定义：返回二个浮点数的较小者
double fmin ( double x, double y );
fmin
fminf
fminl
#include <iostream>
#include <cmath>int main()
{std::cout << "fmin(2,1) = " << std::fmin(2,1) << '\n'<< "fmin(-Inf,0) = " << std::fmin(-INFINITY,0) << '\n'<< "fmin(NaN,-1) = " << std::fmin(NAN,-1) << '\n';
}
//输出
fmin(2,1) = 1
fmin(-Inf,0) = -inf
fmin(NaN,-1) = -1
8. 两个浮点值的正数差（ max(0, x-y) ）
基础定义：返回 x 与 y 间的正差，即若 x>y 则返回 x-y ，否则（若 x≤y ）返回 +0 。
double fdim ( double x, double y );
fdim
fdimf
fdiml
#include <iostream>
#include <cmath>
#include <cerrno>
#include <cstring>
#include <cfenv>
#pragma STDC FENV_ACCESS ON
int main()
{std::cout << "fdim(4, 1) = " << std::fdim(4, 1)<< " fdim(1, 4) = " << std::fdim(1, 4) << '\n'<< "fdim(4,-1) = " << std::fdim(4, -1)<< " fdim(1,-4) = " << std::fdim(1, -4) << '\n';// 错误处理errno = 0;std::feclearexcept(FE_ALL_EXCEPT);std::cout << "fdim(1e308, -1e308) = " << std::fdim(1e308, -1e308) << '\n';if (errno == ERANGE)std::cout << " errno == ERANGE: " << std::strerror(errno) << '\n';if (std::fetestexcept(FE_OVERFLOW))std::cout << " FE_OVERFLOW raised\n";
}
//输出
fdim(4, 1) = 3 fdim(1, 4) = 0
fdim(4,-1) = 5 fdim(1,-4) = 5
fdim(1e308, -1e308) = inferrno == ERANGE: Numerical result out of rangeFE_OVERFLOW raised
2. 指数函数
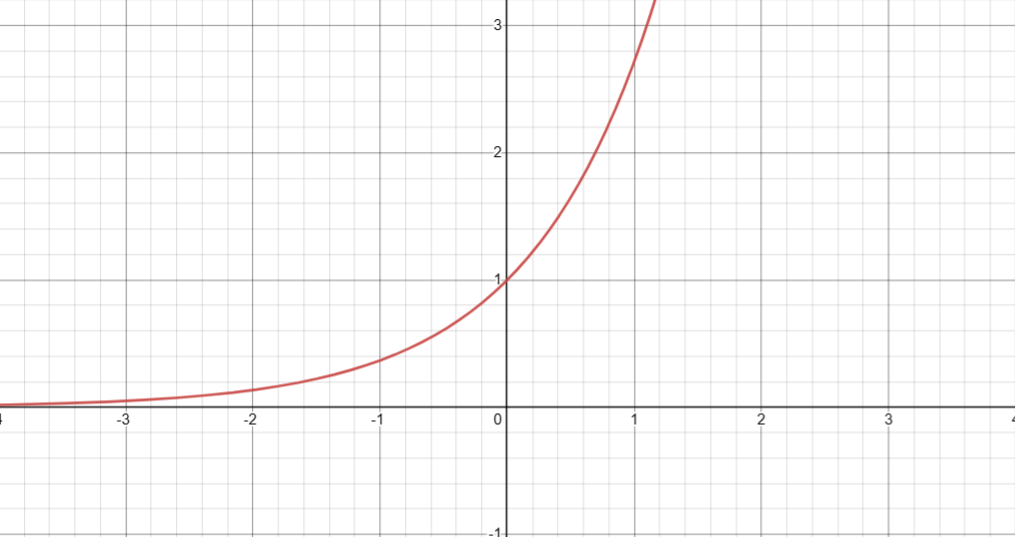
1. 返回 e 的给定次幂（ ex ）
基础定义
double exp ( double arg );
exp
expf
expl
图像
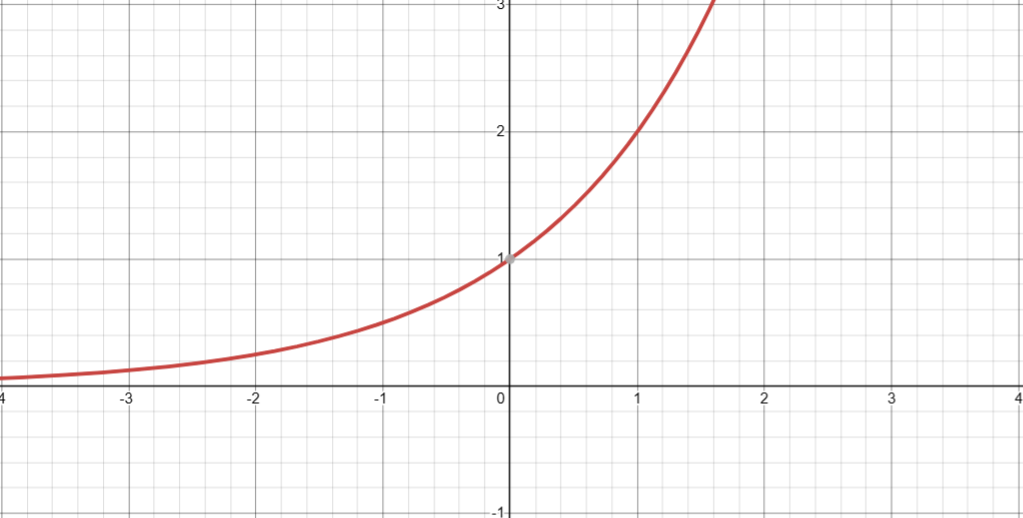
2. 返回 2 的给定次幂（ 2x ）
基础定义
double exp2 ( double n );
exp2
exp2f
exp2l
图像
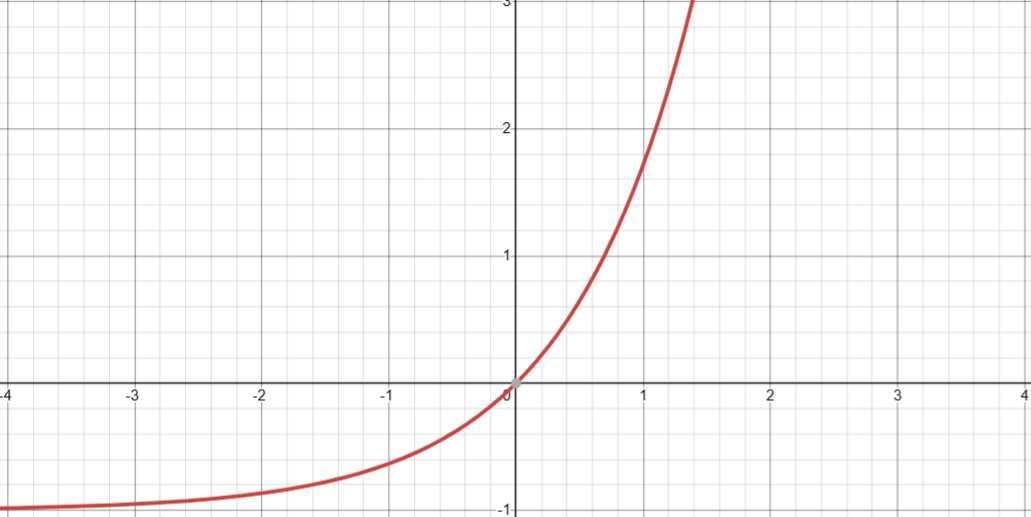
3. 返回 e 的给定次幂减一（ ex-1 ）
基础定义：
double expm1 ( double arg );`在这里插入代码片`
expm1
expm1f
expm1l
图像
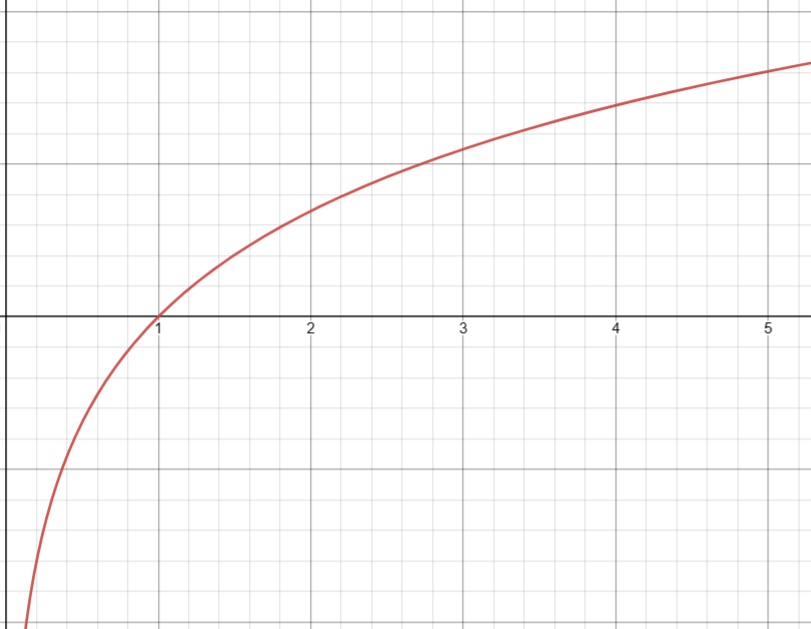
4. 自然（以 e 为底）对数（ ln(x) ）
基础定义
double log ( double arg );
log
logf
logl
图像
5. 常用（以 10 为底）对数（ log10(x) ）
基础定义
double log10 ( double arg );
log10
log10f
log10l
图像
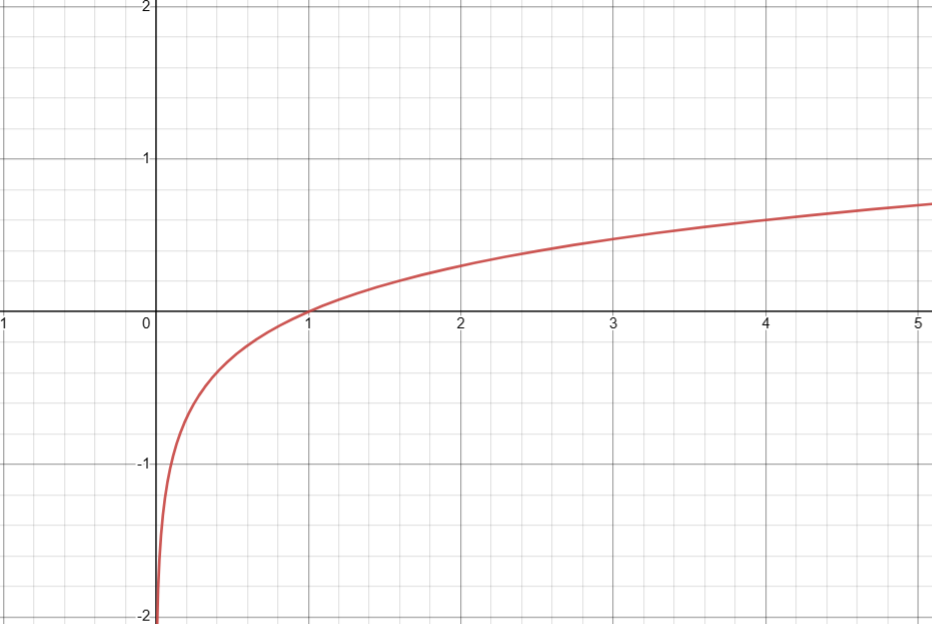
6. 给定数值的以 2 为底的对数（ log2(x) ）
基础定义
double log2 ( double arg );
log2
log2f
log2l
图像
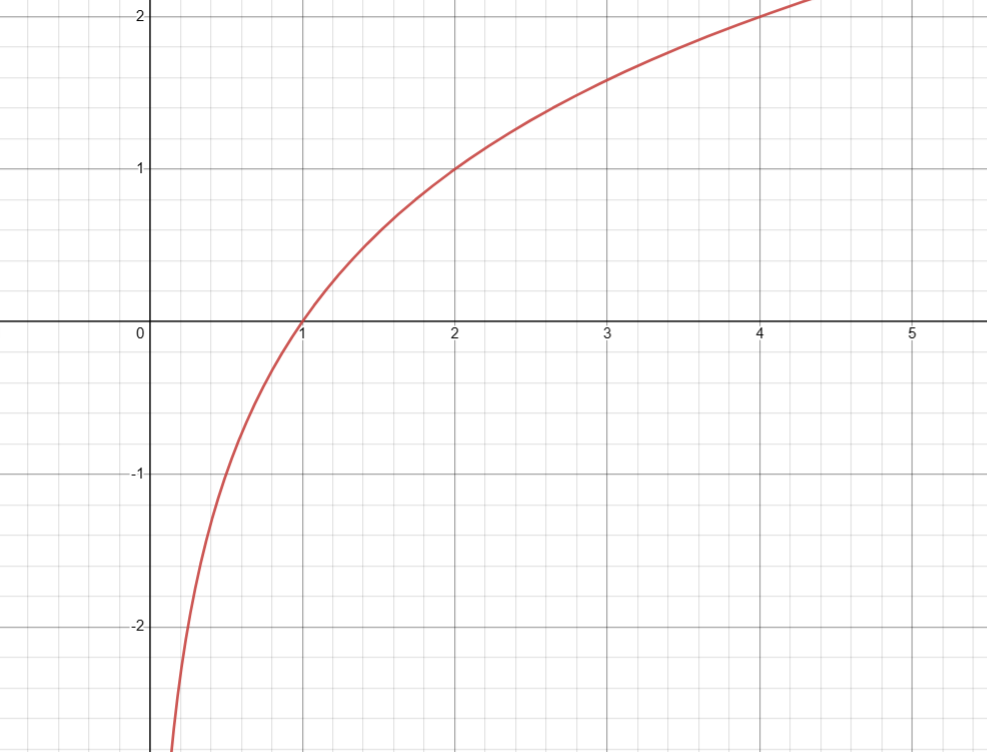
7. 加上给定数值的自然（以 e 为底）对数（ ln(1+x) ）
基础定义
double log1p ( double arg );
log1p
log1pf
log1pl
图像
3. 幂函数
1. 求某数的给定次幂（ xy ）
基础定义
double pow ( double base, double exp );
pow
powf
powl
2. 计算平方根（ √x ）
基础定义
double sqrt ( double arg );
sqrt
sqrtf
sqrtl
3. 计算立方根（ 3√x ）
基础定义
double cbrt ( double arg );
cbrt
cbrtf
cbrtl
4. 计算两个给定数的平方和的平方根（ √x2+y2 ）
基础定义
double hypot ( double x, double y );
hypot
hypotf
hypotl
4. 三角函数
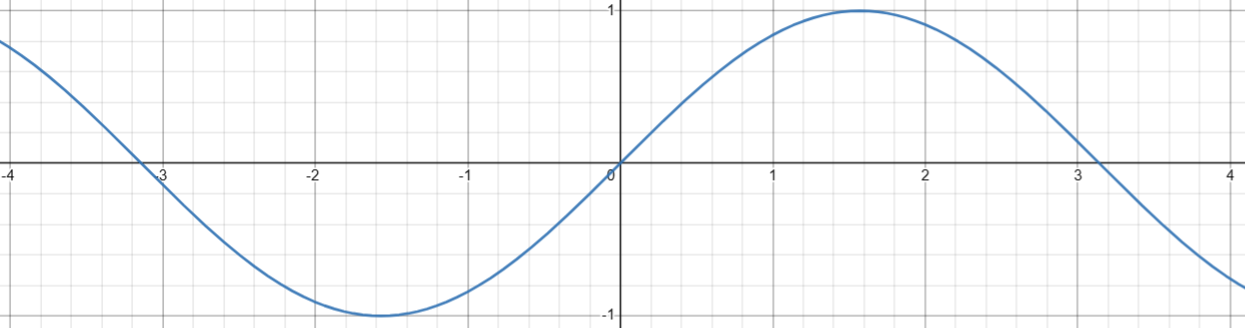
1. 计算正弦（ sin(x) ）
基础定义
double sin ( double arg );
sin
sinf
sinl
图像
2. 计算余弦（ cos(x) ）
基础定义
double cos ( double arg );
cos
cosf
cosl
图像
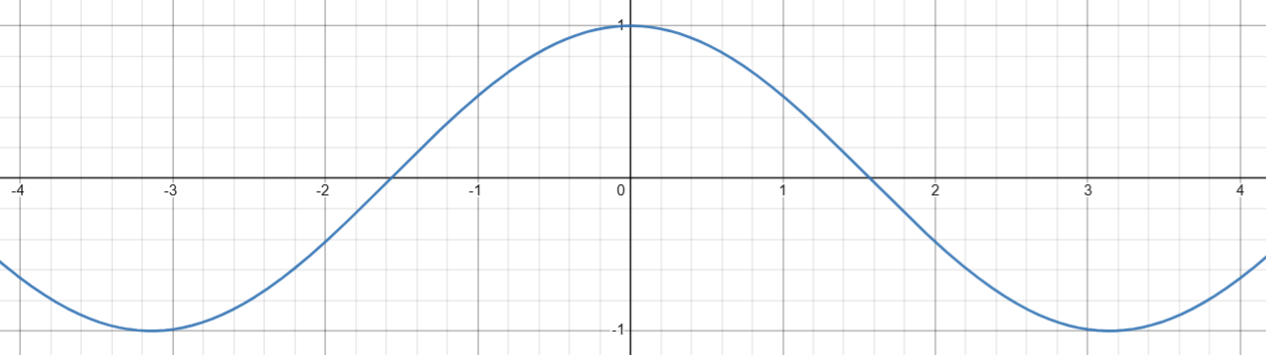
3. 计算正切（ tan(x) ）
基础定义
double tan ( double arg );
tan
tanf
tanl
图像
4. 计算反正弦（ arcsin(x) ）
基础定义
double asin ( double arg );
asin
asinf
asinl
图像
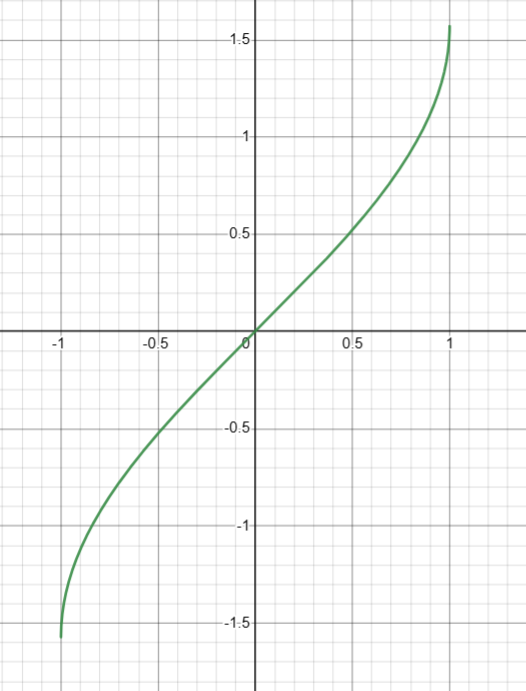
5. 计算反余弦（ arccos(x) ）
基础定义
double acos ( double arg );
acos
acosf
acosl
图像
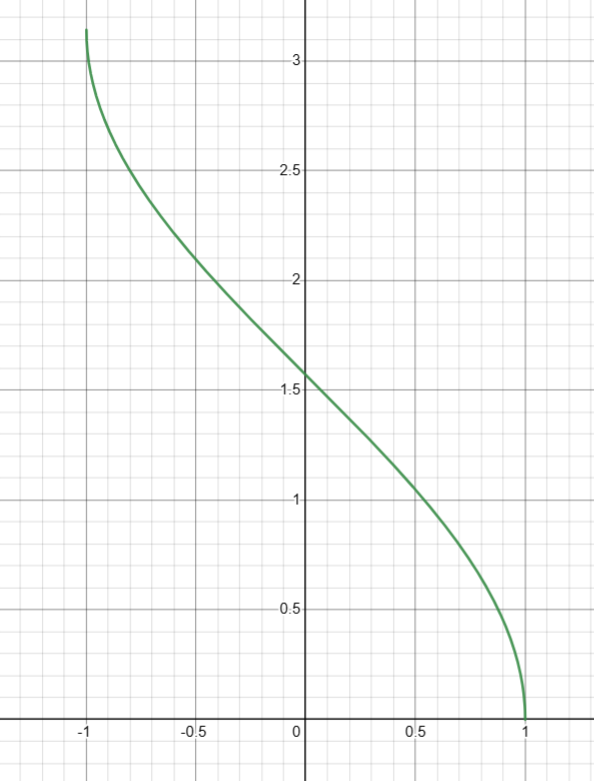
6. 计算反正切（ arctan(x) ）
基础定义
double atan ( double arg );
atan
atanf
atanl
图像
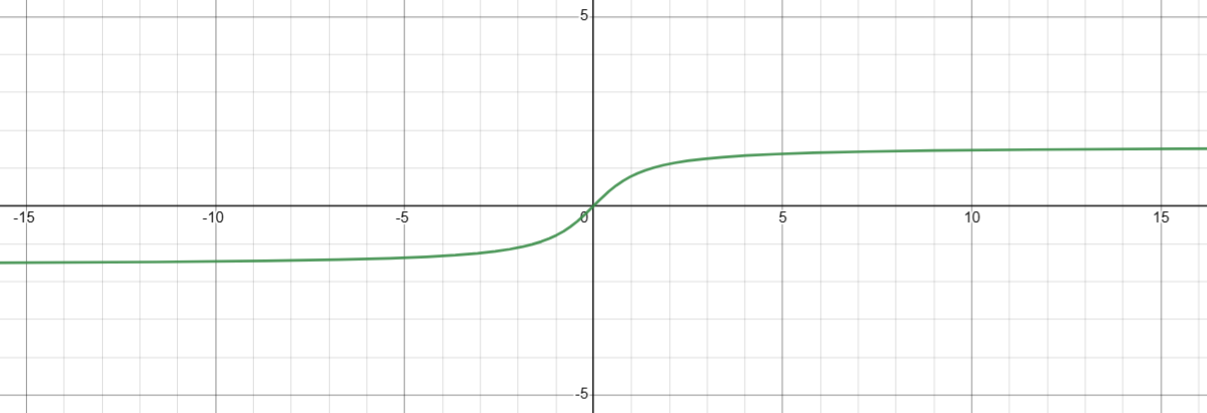
7. 反正切，用符号确定象限
基础定义
double atan2 ( double y, double x );
atan2
atan2f
atan2l
5. 双曲函数
1. 计算双曲正弦（ sinh(x) ）
基础定义
double sinh ( double arg );
sinh
sinhf
sinhl
图像
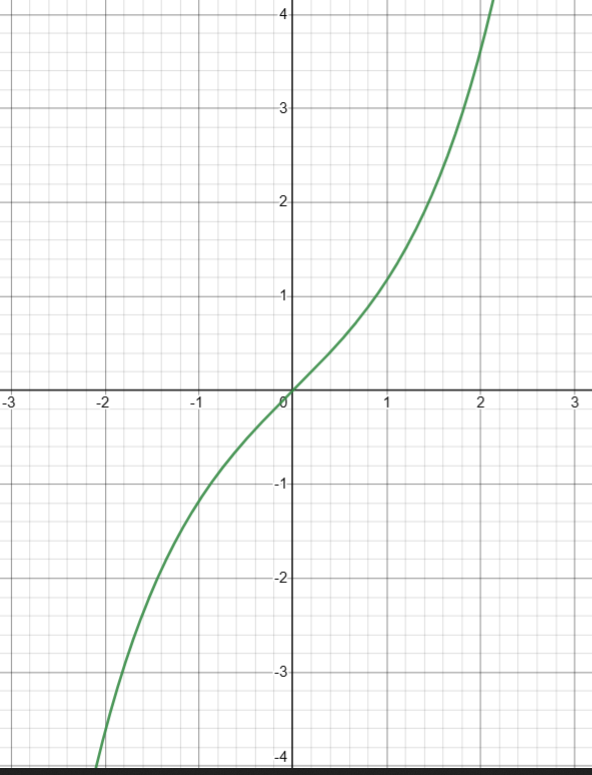
2. 计算双曲余弦（ cosh(x) ）
基础定义
double cosh ( double arg );
cosh
coshf
coshl
图像
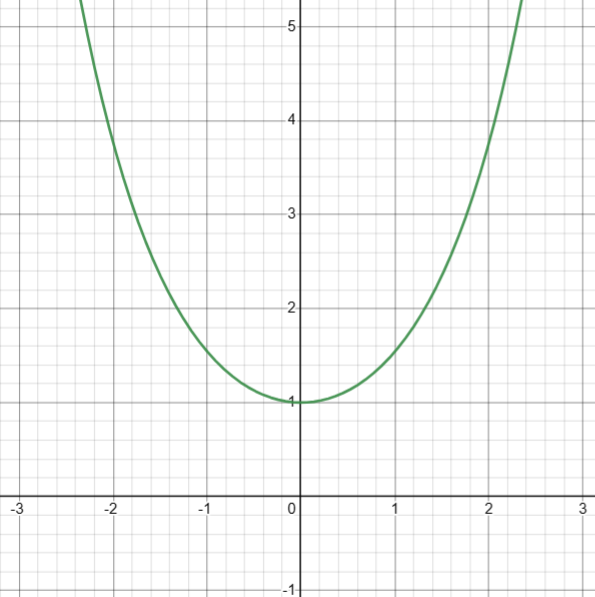
3. 计算双曲正切（ tanh(x) ）
基础定义
double tanh ( double arg );
tanh
tanhf
tanhl
图像
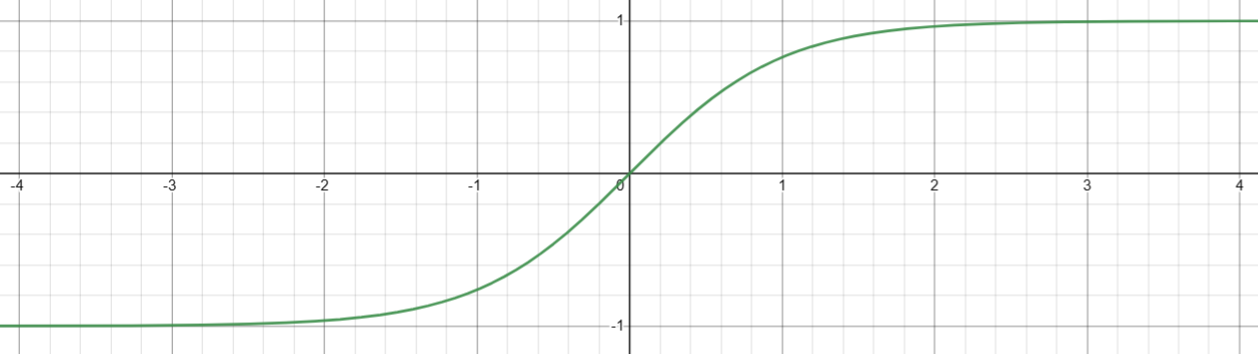
4. 计算反双曲正弦（ arsinh(x) ）
基础定义
double asinh ( double arg );
asinh
asinhf
asinhl
图像
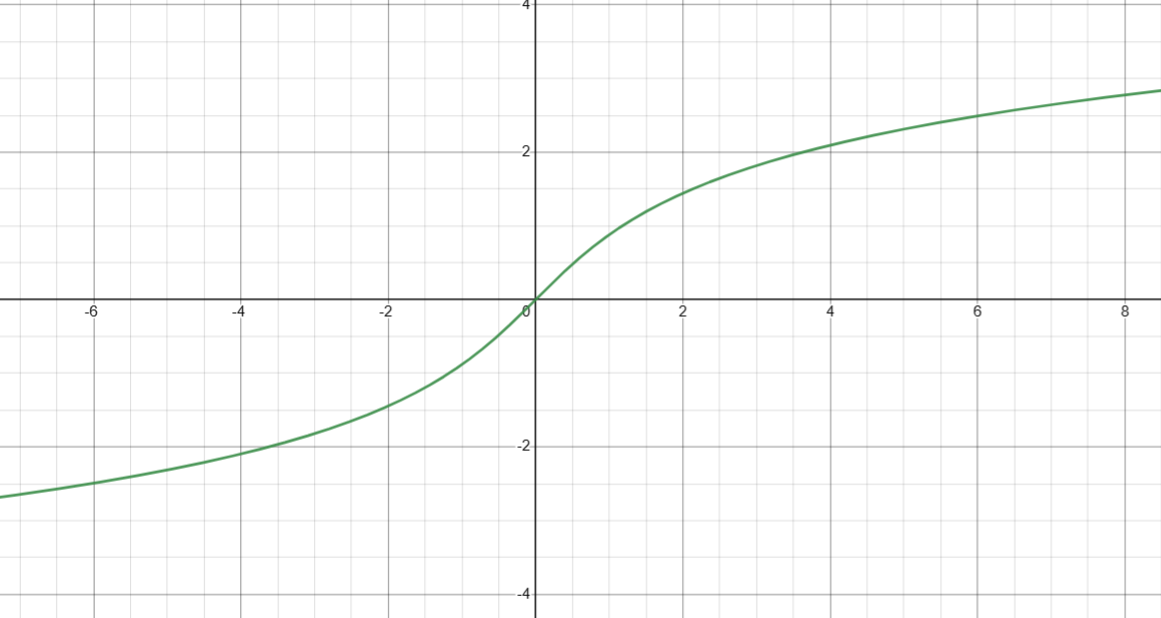
5. 计算反双曲余弦（ arcosh(x) ）
基础定义
double acosh ( double arg );
acosh
acoshf
acoshl
图像
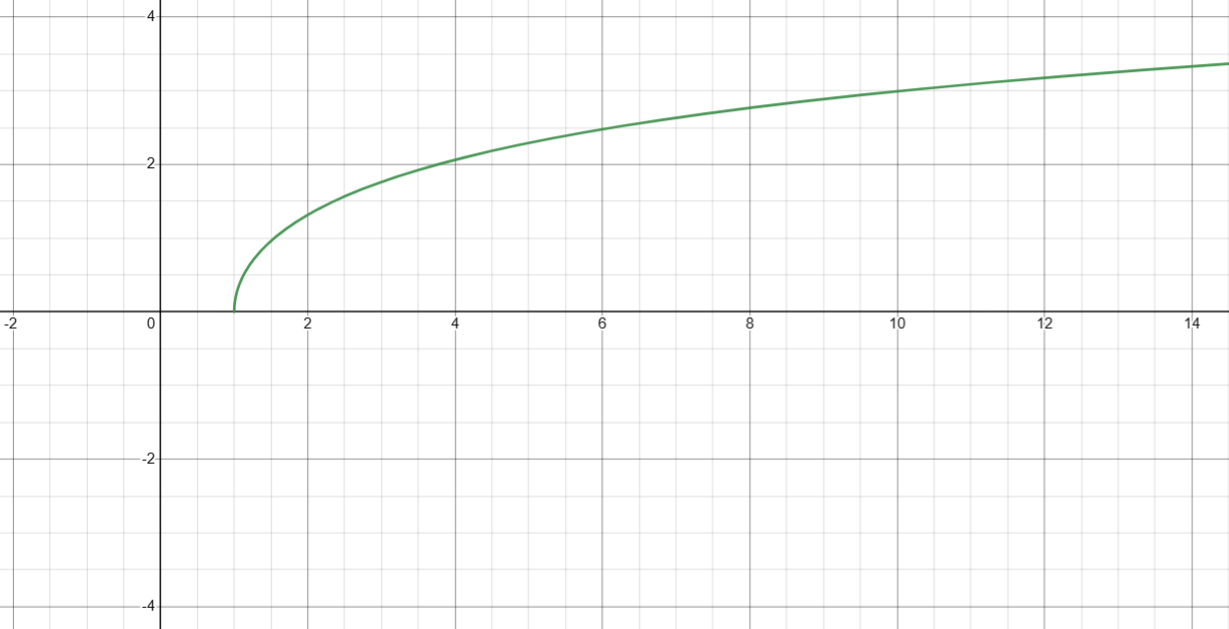
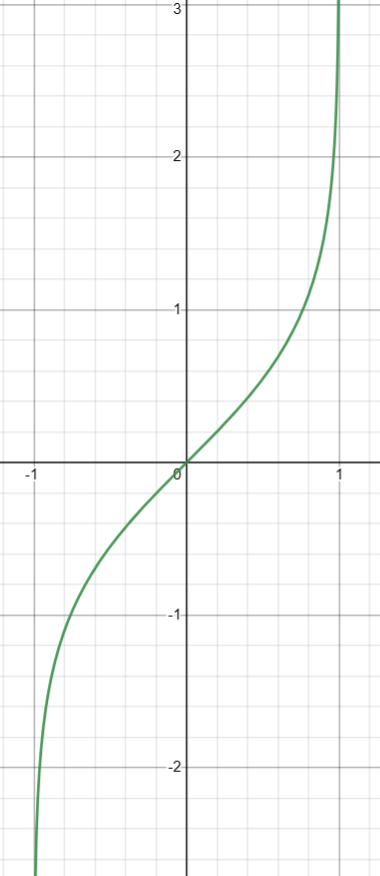
6. 计算反双曲正切（ artanh(x) ）
基础定义
double atanh ( double arg );
atanh
atanhf
atanhl
图像
6. 误差与伽马函数
1. 误差函数
erf
erff
erfl
2. 补误差函数
erfc
erfcf
erfcl
3. gamma 函数
tgamma
tgammaf
tgammal
4. gamma 函数的自然对数
lgamma
lgammaf
lgammal
7. 最接近整数的浮点运算
1. 不小于给定值的最接近整数值
基础定义：计算不小于 arg 的最小整数值。
double ceil ( double arg );
ceil
ceilf
ceill
#include <cmath>
#include <iostream>
int main()
{std::cout << std::fixed<< "floor(+2.7) = " << std::floor(+2.7) << '\n'<< "floor(-2.7) = " << std::floor(-2.7) << '\n'<< "floor(-0.0) = " << std::floor(-0.0) << '\n'<< "floor(-Inf) = " << std::floor(-INFINITY) << '\n';
}//输出：
floor(+2.7) = 2.000000
floor(-2.7) = -3.000000
floor(-0.0) = -0.000000
floor(-Inf) = -inf
2. 不大于给定值的最接近整数
基础定义：计算不大于 arg 的最大整数值。
#include <cmath>
#include <iostream>
int main()
{std::cout << std::fixed<< "floor(+2.7) = " << std::floor(+2.7) << '\n'<< "floor(-2.7) = " << std::floor(-2.7) << '\n'<< "floor(-0.0) = " << std::floor(-0.0) << '\n'<< "floor(-Inf) = " << std::floor(-INFINITY) << '\n';
}//输出：
floor(+2.7) = 2.000000
floor(-2.7) = -3.000000
floor(-0.0) = -0.000000
floor(-Inf) = -inf
3. 绝对值不大于给定值的最接近整数
基础定义：计算绝对值不大于 arg 的最接近整数。
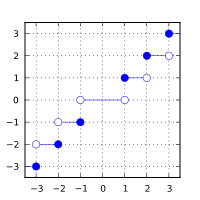
#include <cmath>
#include <iostream>
int main()
{std::cout << std::fixed<< "trunc(+2.7) = " << std::trunc(+2.7) << '\n'<< "trunc(-2.9) = " << std::trunc(-2.9) << '\n'<< "trunc(-0.0) = " << std::trunc(-0.0) << '\n'<< "trunc(-Inf) = " << std::trunc(-INFINITY) << '\n';
}// 可能的输出：
trunc(+2.7) = 2.000000
trunc(-2.9) = -2.000000
trunc(-0.0) = -0.000000
trunc(-Inf) = -inf
4. 最接近整数，中间情况下向远离零舍入
基础定义：计算 arg 的最接近整数值（以浮点格式），中点情况舍入为远离零，无关乎当前舍入模式。 计算 arg 的最接近整数值（以整数格式），中点情况舍入为远离零，无关乎当前舍入模式。
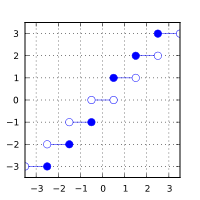
#include <iostream>
#include <cmath>
#include <cfenv>
#include <climits>#pragma STDC FENV_ACCESS ONint main()
{// roundstd::cout << "round(+2.3) = " << std::round(2.3)<< " round(+2.5) = " << std::round(2.5)<< " round(+2.7) = " << std::round(2.7) << '\n'<< "round(-2.3) = " << std::round(-2.3)<< " round(-2.5) = " << std::round(-2.5)<< " round(-2.7) = " << std::round(-2.7) << '\n';std::cout << "round(-0.0) = " << std::round(-0.0) << '\n'<< "round(-Inf) = " << std::round(-INFINITY) << '\n';// lroundstd::cout << "lround(+2.3) = " << std::lround(2.3)<< " lround(+2.5) = " << std::lround(2.5)<< " lround(+2.7) = " << std::lround(2.7) << '\n'<< "lround(-2.3) = " << std::lround(-2.3)<< " lround(-2.5) = " << std::lround(-2.5)<< " lround(-2.7) = " << std::lround(-2.7) << '\n';std::cout << "lround(-0.0) = " << std::lround(-0.0) << '\n'<< "lround(-Inf) = " << std::lround(-INFINITY) << '\n';// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "std::lround(LONG_MAX+1.5) = "<< std::lround(LONG_MAX+1.5) << '\n';if (std::fetestexcept(FE_INVALID))std::cout << " FE_INVALID was raised\n";
}//可能的输出：
round(+2.3) = 2 round(+2.5) = 3 round(+2.7) = 3
round(-2.3) = -2 round(-2.5) = -3 round(-2.7) = -3
round(-0.0) = -0
round(-Inf) = -inf
lround(+2.3) = 2 lround(+2.5) = 3 lround(+2.7) = 3
lround(-2.3) = -2 lround(-2.5) = -3 lround(-2.7) = -3
lround(-0.0) = 0
lround(-Inf) = -9223372036854775808
std::lround(LONG_MAX+1.5) = -9223372036854775808FE_INVALID was raised
5. 使用当前舍入模式的最接近整数
6. 使用当前舍入模式的最接近整数
若结果有别则有异常
8. 浮点操作函数
9. 分类与比较
三、宏常量
四、错误处理
相关文章：
C++参悟：数值运算相关
数值运算相关 一、概述二、常用数学函数1. 基础运算1. 浮点值的绝对值（ |x| ）2. 浮点除法运算的余数3. 除法运算的有符号余数4. 除法运算的有符号余数和最后三个二进制位5. 混合的乘加运算6. 两个浮点值的较大者7. 两个浮点值的较小者8. 两个浮点值的正数…...
【Web前端开发基础】CSS的定位和装饰
CSS的定位和装饰 目录 CSS的定位和装饰一、学习目标二、文章内容2.1 定位2.1.1 定位的基本介绍2.1.2 定位的基本使用2.1.3 静态定位2.1.4 相对定位2.1.5 绝对定位2.1.6 子绝父相2.1.7 固定定位2.1.8元素的层级关系 2.2 装饰2.2.1 垂直对齐方式2.2.2 光标类型2.2.3 边框圆角2.2.…...
[pytorch入门] 3. torchvision中的transforms
torchvision中的transforms 是transforms.py工具箱，含有totensor、resize等工具 用于将特定格式的图片转换为想要的图片的结果，即用于图片变换 用法 在transforms中选择一个类创建对象，使用这个对象选择相应方法进行处理 能够选择的类 列…...
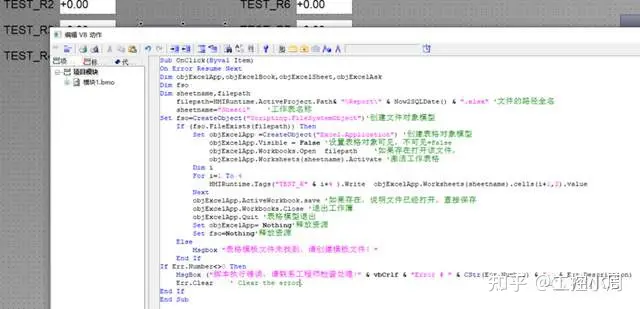
WINCC读写EXCEL-VBS
原创 RENHQ WINCC 关于VBS操作EXCEL的文档不管在论坛上还是在网上，相关的脚本已经很多，但是依然有很多人在问这个问题，于是把我以前在论坛上发的一个集合帖子的脚本拿来，重新开个帖子，如果再有人问的话，可…...
Python os模块
简介 Python的os模块是一个标准库模块，用于提供与操作系统相关的功能（相当于接口）。os模块允许Python程序与文件系统、目录结构、进程管理等操作系统级别的功能进行交互。 主要功能 文件和目录操作 创建、删除、重命名文件和目录…...
Elasticsearch：2023 年 Lucene 领域发生了什么？
作者：来自 Elastic Adrien Grand 2023 年刚刚结束，又是 Apache Lucene 开发活跃的一年。 让我们花点时间回顾一下去年的亮点。 社区 2023 年，有： 5 个次要版本（9.5、9.6、9.7、9.8 和 9.9），1 …...
Java算法 leetcode简单刷题记录4
Java算法 leetcode简单刷题记录4 买卖股票的最佳时机： https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/ 笨办法： 记录当天的值及之后的最大值，相减得到利润； 所有的天都计算下，比较得到利润最大值&…...
opencv#27模板匹配
图像模板匹配原理 例如给定一张图片，如上图大矩阵所示，然后给定一张模板图像，如上图小矩阵。 我们在大图像中去搜索与小图像中相同的部分或者是最为相似的内容。比如我们在图像中以灰色区域给出一个与模板图像尺寸大小一致的区域，…...
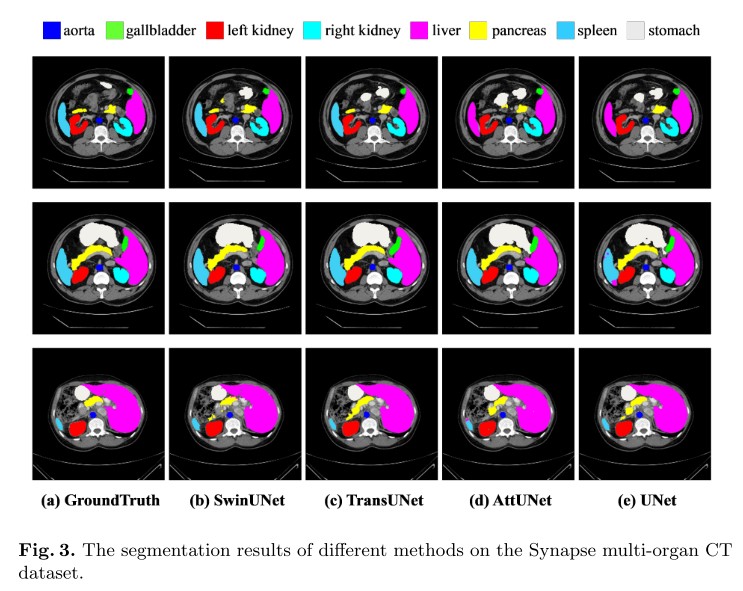
【论文阅读笔记】Swin-Unet: Unet-like Pure Transformer for Medical Image Segmentation
1.介绍 Swin-Unet: Unet-like Pure Transformer for Medical Image Segmentation Swin-Unet：用于医学图像分割的类Unet纯Transformer 2022年发表在 Computer Vision – ECCV 2022 Workshops Paper Code 2.摘要 在过去的几年里，卷积神经网络ÿ…...
IS-IS：01 ISIS基本配置
这是实验拓扑，下面是基本配置： R1: sys sysname R1 user-interface console 0 idle-timeout 0 0 int loop 0 ip add 1.1.1.1 24 int g0/0/0 ip add 192.168.12.1 24 qR2: sys sysname R2 user-interface console 0 idle-timeout 0 0 int loop 0 ip add …...
基于极限学习机的曲线分类，基于极限学习机的光谱分类，基于极限学习机的分类预测
目录 背影 极限学习机 基于极限学习机的曲线分类，基于极限学习机的光谱分类，基于极限学习机的分类预测 主要参数 MATLAB代码 效果图 结果分析 展望 完整代码下载链接：基于极限学习机的曲线分类，基于极限学习机的光谱分类，基于极限学习机的分类预测的MATLAB代码资源-CSDN…...
miniconda安装
Miniconda是一个小型版的Anaconda，它包含了一个包管理工具conda和Python。Miniconda适用于那些只需要管理Python包和环境，而不需要Anaconda中包含的大部分科学计算工具的用户。 Miniconda的安装过程相对简单。你可以从清华大学开源软件镜像站下载Minico…...
访问的方法总结)
PHP判断访客是否手机端(移动端浏览器)访问的方法总结
PHP判断访客是否手机端、移动端、浏览器访问的方法总结 方法一：使用$_SERVER全局变量方法二：使用PHP的get_browser函数方法三：使用第三方库（Mobile Detect）方法四：使用WURFL设备数据库 方法一：使…...
vscode无法自动补全
前提：安装c/c插件 c/c插件功能非常强大，几乎能满足日常编码过程中常用的功能；因此也包含自动补全的功能，开启方法如下： 文件->首选项->设置： 扩展->c/c->Intellisense，找到Intell…...
深度学习记录--指数加权平均
指数加权移动平均(exponentially weighted moving averages) 如何对杂乱的数据进行拟合？ 通过指数加权平均可以把数据图近似拟合成一条曲线 公式： 其中表示第t个平均数，表示第t-1个平均数，表示第t个数据，表示变化参数…...
如何生成图源二维码？
数据是GIS的血液。 自从苹果端与安卓端水经微图APP（简称“微图APP”）上线之后，有用户反馈图源比较少的问题。 其实，微图APP支持通过图源二维码添加自定义图源，而该二维码则可以通过微图Web版生成。 如何生成图源二维…...
PowerShell install 一键部署grafana
grafana 前言 Grafana 是一款开源的数据可视化和监控仪表盘工具。它提供了丰富的数据查询、可视化和报警功能，可用于实时监控、数据分析和故障排除等领域。 通过 Grafana，您可以连接到各种不同的数据源，包括时序数据库（如 Prometheus、InfluxDB）和关系型数据库（如 MySQ…...
笨蛋学设计模式行为型模式-解释器模式【23】
行为型模式-解释器模式 8.10解释器模式8.10.1概念8.10.2场景8.10.3优势 / 劣势8.10.4解释器模式可分为8.10.5解释器模式8.10.6实战8.10.6.1题目描述8.10.6.2输入描述8.10.6.3输出描述8.10.6.4代码 8.10.7总结 8.10解释器模式 8.10.1概念 解释器模式用于定义一个语言的文法…...
SAP ABAP SUBMIT常用用法
导语：一直对SUBMIT的用法模模糊糊，每次用都要去查询，本次痛下决心，腾出时间，梳理了一下，如果本文对你有帮助，点个赞再走～ 之前分享过SUBMIT调用程序获取内表的值，就不重…...
)
GitLab备份与恢复测试(基于Docker)
GitLab环境准备 docker run --name gitlab \ -p 2022:22 -p 2080:80 -p 2443:443 -d \ -v /opt/gitlab/config:/etc/gitlab \ -v /opt/gitlab/gitlab/logs:/var/log/gitlab \ -v /opt/gitlab/gitlab/data:/var/opt/gitlab \ gitlab/gitlab-ce:16.2.1-ce.0备份 1.修改配置文件…...
高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个？3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制（过半机制࿰…...
条件运算符
C中的三目运算符（也称条件运算符，英文：ternary operator）是一种简洁的条件选择语句，语法如下： 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true，则整个表达式的结果为“表达式1”…...
服务器硬防的应用场景都有哪些？
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式，避免服务器受到各种恶意攻击和网络威胁，那么，服务器硬防通常都会应用在哪些场景当中呢？ 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...
el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
（二）原型模式
原型的功能是将一个已经存在的对象作为源目标，其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现，忽略对象创建过程中的其它细节。 📌 核心特点： 避免重复初…...
《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术，说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号（调制） 把信息从信号中抽取出来&am…...
P3 QT项目----记事本（3.8）
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户，但你不希望用 root 权限运行 ns-3（这是对的，ns3 工具会拒绝 root），你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案：创建非 roo…...
Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器，其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机（Virtual Host）。 1. 简介 Nginx 使用 server_name 指令来确定…...
群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...