B. Sherlock and his girlfriend
Sherlock has a new girlfriend (so unlike him!). Valentine's day is coming and he wants to gift her some jewelry.
He bought n pieces of jewelry. The i-th piece has price equal to i + 1, that is, the prices of the jewelry are 2, 3, 4, ... n + 1.
Watson gave Sherlock a challenge to color these jewelry pieces such that two pieces don't have the same color if the price of one piece is a prime divisor of the price of the other piece. Also, Watson asked him to minimize the number of different colors used.
Help Sherlock complete this trivial task.
Input
The only line contains single integer n (1 ≤ n ≤ 100000) — the number of jewelry pieces.
Output
The first line of output should contain a single integer k, the minimum number of colors that can be used to color the pieces of jewelry with the given constraints.
The next line should consist of n space-separated integers (between 1 and k) that specify the color of each piece in the order of increasing price.
If there are multiple ways to color the pieces using k colors, you can output any of them.
Examples
input
Copy
3
output
Copy
2 1 1 2
input
Copy
4
output
Copy
2 2 1 1 2
Note
In the first input, the colors for first, second and third pieces of jewelry having respective prices 2, 3 and 4 are 1, 1 and 2 respectively.
In this case, as 2 is a prime divisor of 4, colors of jewelry having prices 2 and 4 must be distinct.
夏洛克有了一个新女友(真不像他!)。情人节快到了,他想送她一些珠宝。
他买了n件珠宝。第i件的价格等于i+1,也就是说,这些珠宝的价格是2,3,4,...n+1。
华生给夏洛克出了个难题:给这些珠宝上色,如果其中一件的价格是另一件价格的质除数,那么两件珠宝的颜色就不会相同。此外,华生还要求他尽量减少使用不同颜色的数量。
请帮助夏洛克完成这个微不足道的任务。
输入
唯一的一行包含单个整数n(1≤n≤100000)--珠宝的数量。
输出
第一行输出应包含一个整数k,即在给定的约束条件下,可以用来给珠宝片着色的最小颜色数。
下一行应该包含n个空格分隔的整数(在1和k之间),这些整数按照价格递增的顺序指定每件珠宝的颜色。
如果有多种方法可以用k种颜色给珠宝上色,你可以输出其中任何一种。
例子
inputCopy
3
outputCopy
2
1 1 2
输入复制
4
输出拷贝
2
2 1 1 2
备注
在第一个输入中,价格为2、3、4的第一件、第二件和第三件珠宝的颜色分别为1、1和2。
在这种情况下,由于2是4的质除数,价格为2和4的珠宝的颜色必须是不同的。
解析,比赛的时候连题目都没看明白,就在那里框框写然后框框wa
是真的没看明白质因数是啥意思然后看样例有个2和4然后就彻底理解错了
 比赛完翻了好题解才算是明白,这个题目就是单纯的判断质数 的题目,是真的没看懂,吸取教训了
比赛完翻了好题解才算是明白,这个题目就是单纯的判断质数 的题目,是真的没看懂,吸取教训了
欧拉筛,欧拉筛,筛出质数。在强记板子
bool book[N] = { 1,1 };
void ol()
{for (int i = 2;i <= 100010;i++){if (!book[i])arr[++k] = i;for (int j = 1;j <= k;j++){if (i * arr[j] > 100010)break;book[i * arr[j]] = 1;if (i % arr[j] == 0)break;}}
}ac代码
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<cstring>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b) for(int i=a;i<=b;i++)
#define rrep(a,b) for(int j=a;j<=b;j++)
#define per(a,b) for(int i=a;i>=b;i--)
#define pper(a,b) for(int j=a;j>=b;j--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
const int N = 2e5 + 100;
const int INF = 0x3f3f3f3f;
ll gcdd(ll a, ll b)
{if (b) while ((a %= b) && (b %= a));return a + b;
}
ll h[N], ne[N], w[N], to[N], idx;
void add(int a, int b, int c)
{to[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
const int mod = 998244353;
ll t, n, m, a, b, c, x, k, cnt, ans, ant, sum, p;
ll arr[N], brr[N], crr[N];
bool book[N] = { 1,1 };
void ol()
{for (int i = 2;i <= 100010;i++){if (!book[i])arr[++k] = i;for (int j = 1;j <= k;j++){if (i * arr[j] > 100010)break;book[i * arr[j]] = 1;if (i % arr[j] == 0)break;}}
}
int main()
{ol();cin >> n;if (n <= 2){cout << 1 << endl;}else{cout << 2 << endl;}for (int i = 2;i <= n + 1;i++){if (!book[i]){cout << 1 << ' ';}else{cout << 2 << ' ';}}
}相关文章:

B. Sherlock and his girlfriend
Sherlock has a new girlfriend (so unlike him!). Valentines day is coming and he wants to gift her some jewelry. He bought n pieces of jewelry. The i-th piece has price equal to i 1, that is, the prices of the jewelry are 2, 3, 4, ... n 1. Watson…...

Spring SpEL表达式
Java知识点总结:想看的可以从这里进入 目录17、Spring SpEL17.1、简介17.2、配合value使用17.2.1、基本字面值17.2.2、类相关表达式17.2.3、properties17.2.4、T运算符17.2.5、new17.2.6、Elvis运算符17.2.7、运算符17.2、配合XML使用17、Spring SpEL 17.1、简介 S…...

Nginx反向代理原理详解与配置
Nginx反向代理是一种常用的反向代理技术,它允许您将一个或多个Web服务器上的内容公开给Internet上的客户端,而不必暴露您的服务器的IP地址。Nginx反向代理的原理是:客户端发出一个HTTP请求,Nginx服务器收到请求后,将请…...

Happen-Before从入门到踹门
什么是Happen-Before有人翻译为"先行发生原则",其实也没错,但是更准确的说法应该是,前一个操作的值,后一个总能察觉到。Happen-Before的八条规则程序有序性:在前面的代码优先于在后面的代码执行volatile的变…...

电力系统系统潮流分析【IEEE 57 节点】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
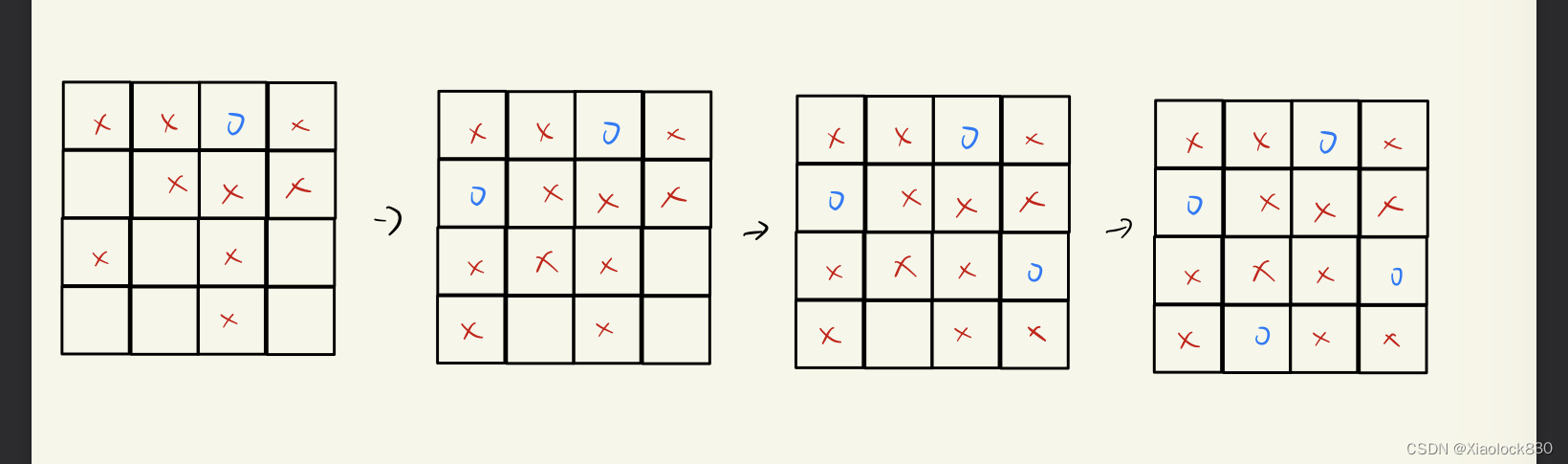
Java——N皇后问题
题目链接 leetcode在线oj题——N皇后 题目描述 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ÿ…...
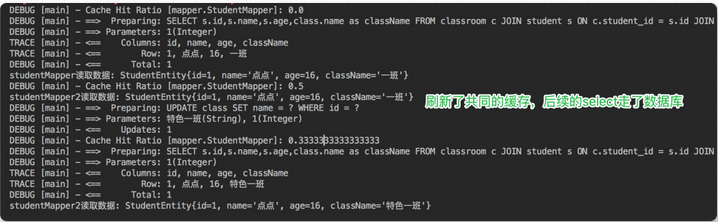
Mybatis一级缓存与二级缓存
一、MyBatis 缓存缓存就是内存中的数据,常常来自对数据库查询结果的保存。使用缓存,我们可以避免频繁与数据库进行交互,从而提高响应速度。MyBatis 也提供了对缓存的支持,分为一级缓存和二级缓存,来看下下面这张图&…...
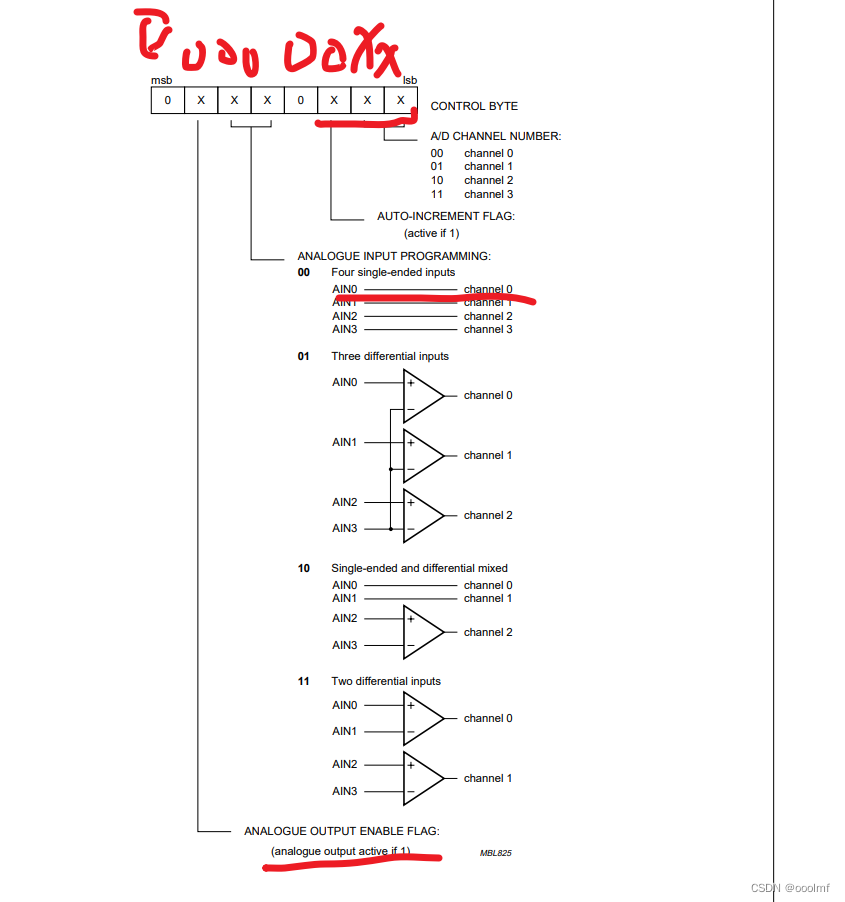
LQB,手打,PCF8591,ADDA转换,AD1是光敏电阻,AD3是电位器,DA输出
在上述at24c02de 基础上,添加三个函数 一个是读取通道1光敏电阻的数据; 一个是读取通道3的电压; 一个是输出DA的数据。。 5V的AD DA。 如果读入的电压是5V,输入AD,就是255; 如果是0V,就是00000…...

【计组笔记06】计算机组成与原理之控制器和总线结构
这篇文章,主要介绍计算机组成与原理之控制器和总线结构。 目录 一、控制器功能 1.1、控制器组成 1.2、控制单元的输入和输出...

elisp简单实例: auto-save
elisp 能找一个简单又实用的代码很不容易,以下代码不是我的原创,只是结合自己的理解,添加修正了一些注释,荣誉归原作者,感谢原作者的开源精神! 调用说明: 把后面代码存为auto-save.el 在init.el 中写上 (require auto-save) 就可以了. 下面是auto-save.el 内容了. ;; 我…...

写字楼/园区/购物中心空置率太高?快用快鲸智慧楼宇系统
客户租不租你的写字楼,事关区位、交通、环境、价格、面积、装修等诸多因素,但很多招商部对这些影响客户决策的数据并不重视,在客户初次上门看房时仅简单记录姓名、联系方式、需求面积,对其他核心数据熟视无睹,也为日后…...
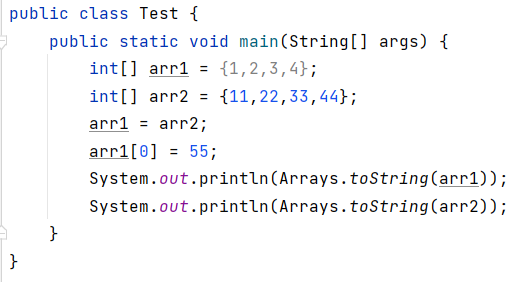
【JavaSE】数组的定义和使用(上)
数组的定义和使用(上)6-数组的定义与使用1. 数组的基本概念1.1 为什么要使用数组1.2 什么是数组1.3 数组的创建及初始化1.3.1 数组的创建1.3.2 数组的初始化1.4 数组的使用1.4.1 数组中元素的访问1.4.2 遍历数组2. 数组是引用类型2.1 初始JVM的内存分布2…...

计算机的学习路线
本文是介绍如何成为一个Geek,一个真正的计算机高手。 适合有成为IT领域技术大牛的人参考。 写给大一新生和所有向深耕IT领域的人,避免走一些弯路。 第一门入门的必备功课-语法与算法 什么是计算机? 用来做运算的机器 电子计算机在运算方面…...

TD算法超详细解释,一篇文章看透彻!
【已解决】TD算法超详细解释和实现(Sarsa,n-step Sarsa,Q-learning)一篇文章看透彻! 郑重声明:本系列内容来源 赵世钰(Shiyu Zhao)教授的强化学习数学原理系列,本推文出于非商业目的分享个人学习…...
4.1 路由器(华硕 官改/梅林 华为 小米 路由) 使用花生壳 实现远程管理
最近添置了一台华硕的八爪鱼GT AC5300,到手后刷了官改,而里面软件中就提供了花生壳程序,想到花生壳为每个用户提供了两条免费映射(带宽为1mbs,流量为1g/月),所以就打算利用来做一个远程访问。具…...
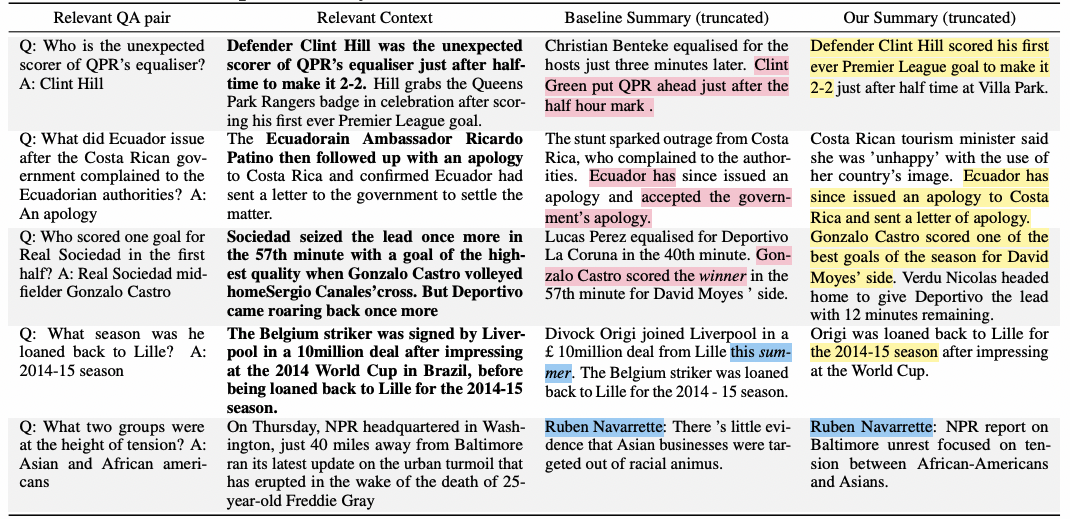
内容算法解读:提高内容摘要与原文的一致性(Faithfulness)
全文摘要:受益于预训练语言模型的发展,应用神经网络模型提取内容摘要的技术也获得了长足进步。但目前还存在一个未被很好解决的问题:神经网络模型提取的摘要不能如实反映原文档的中心思想,没有做到忠实(not faithful&a…...

python用openpyxl包操作xlsx文件,统计表中合作电影数目最多的两个演员
题目🎉🎉🎉:编程完成下面任务:已知excel文件“电影导演演员信息表.xlsx”如下图所示:🍳🍳🍳要求:使用 openpyxl 包操作打开此文件,编写程序统计在…...

Lesson12---人工神经网络(1)
12.1 神经元与感知机 12.1.1 感知机 感知机: 1957, Fank Rosenblatt 由两层神经元组成,可以简化为右边这种,输入通常不参与计算,不计入神经网络的层数,因此感知机是一个单层神经网络 感知机 训练法则&am…...
)
算法练习-排序(二)
算法练习-排序(二) 文章目录算法练习-排序(二)1 合并排序的数组1.1 题目1.2 题解2 有效的字母异位词2.1 题目2.2 题解3 判断能否形成等差数列3.1 题目3.2 题解4 合并区间4.1 题目3.2 题解5 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面5.1 题目5.2 题解6 颜色分类6.1 题目6.…...

202302读书笔记|《长安的荔枝》——只要肯努力,办法总比困难多
202302读书笔记|《长安的荔枝》——只要肯努力,办法总比困难多 《长安的荔枝》这本书真是酣畅淋漓啊,读起来一气呵成,以讲故事的口吻叙述,上林署九品小官员——李善德,兢兢业业工作多年,终于借贷买了房&…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...

OpenHarmony标准系统-HDF框架之I2C驱动开发
文章目录 引言I2C基础知识概念和特性协议,四种信号组合 I2C调试手段硬件软件 HDF框架下的I2C设备驱动案例描述驱动Dispatch驱动读写 总结 引言 I2C基础知识 概念和特性 集成电路总线,由串网12C(1C、12C、Inter-Integrated Circuit BUS)行数据线SDA和串…...
