C语言-算法-最小生成树
【模板】最小生成树
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
输入格式
第一行包含两个整数 N , M N,M N,M,表示该图共有 N N N 个结点和 M M M 条无向边。
接下来 M M M 行每行包含三个整数 X i , Y i , Z i X_i,Y_i,Z_i Xi,Yi,Zi,表示有一条长度为 Z i Z_i Zi 的无向边连接结点 X i , Y i X_i,Y_i Xi,Yi。
输出格式
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
样例 #1
样例输入 #1
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
样例输出 #1
7
提示
数据规模:
对于 20 % 20\% 20% 的数据, N ≤ 5 N\le 5 N≤5, M ≤ 20 M\le 20 M≤20。
对于 40 % 40\% 40% 的数据, N ≤ 50 N\le 50 N≤50, M ≤ 2500 M\le 2500 M≤2500。
对于 70 % 70\% 70% 的数据, N ≤ 500 N\le 500 N≤500, M ≤ 1 0 4 M\le 10^4 M≤104。
对于 100 % 100\% 100% 的数据: 1 ≤ N ≤ 5000 1\le N\le 5000 1≤N≤5000, 1 ≤ M ≤ 2 × 1 0 5 1\le M\le 2\times 10^5 1≤M≤2×105, 1 ≤ Z i ≤ 1 0 4 1\le Z_i \le 10^4 1≤Zi≤104。
样例解释:

所以最小生成树的总边权为 2 + 2 + 3 = 7 2+2+3=7 2+2+3=7。
代码
#include <stdio.h>
#include <stdlib.h>
#define MAXN 300000
#define MAXM 300000
typedef struct // 定义边的结构体
{int u, v, w;
}Edge;
Edge edges[MAXM]; // 存储所有的边
int pa[MAXN]; // 并查集数组,用于判断两个节点是否在同一棵树中
int N, M; // N是节点数,M是边数
int cmp(Edge a, Edge b); // 边的比较函数,按照边的权重从小到大排序
int find(int x); // 并查集的查找函数,用于查找节点x的根节点
int kruskal(); // Kruskal算法函数int main(int argc, char *argv[])
{int i;scanf("%d %d", &N, &M); // 读取节点数和边数for (i = 0; i < M; i++){scanf("%d %d %d", &edges[i].u, &edges[i].v, &edges[i].w);}int res = kruskal(); // 调用Kruskal算法计算最小生成树的权重if (res == -1) // 如果图不连通{printf("orz\n");}else{printf("%d\n", res);}return 0;
}int cmp(Edge a, Edge b) // 边的比较函数,按照边的权重从小到大排序
{return (a.w - b.w);
}int find(int x) // 并查集的查找函数,用于查找节点x的根节点
{while (pa[x] != x){x = pa[x];}return x;
}int kruskal() // Kruskal算法函数
{int i, j;for (i = 0; i < M; i++) // 将所有的边按照从小到大排序{for (j = i + 1; j < M; j++){if (cmp(edges[i], edges[j]) > 0){Edge temp = edges[i];edges[i] = edges[j];edges[j] = temp;}}}for (i = 1; i <= N; i++) // 初始化并查集{pa[i] = i;}int res = 0; // 存储最小生成树的权重int cnt = 0; // 存储当前已经选择的边的数量for (i = 0; i < M; i++) // 遍历所有的边{int u = find(edges[i].u); // 边的一个节点int v = find(edges[i].v); // 边的另一个节点// 如果两个节点不在同一棵树中,说明这条边可以添加到最小生成树中if (u != v){res += edges[i].w; // 更新最小生成树的权重pa[u] = v; // 合并两棵树cnt++; // 更新已经选择的边的数量}}if (cnt != N - 1) // 如果选择边的数量小于N - 1,说明图不连通{return -1;}return res; // 返回最小生成树的权重
}
相关文章:

C语言-算法-最小生成树
【模板】最小生成树 题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 输入格式 第一行包含两个整数 N , M N,M N,M,表示该图共有 N N N 个结点和 M M M 条无向边。 接下来 M M M 行…...

android 扫描某个包下的所有类
注意事项 如果在用Android Studio开发过程中,如果新增了类,扫描不到。只能把APP卸载了,才能扫描到。 可能是Instance Run 的影响。 后面研究一下这篇文章,看看能不能解决 Android 遍历Apk下的所有类文件 package com.trs.nmip.…...

远程ssh 不通的原因之一
背景:我都想大喊一声,我上网是通的, ping网址是通的,ping www.baidu.com 是通的, 怎么都远程不了,报超时;嘿, 别人远程就能行。我都想挠头了。 目录 1. 先 ping 自己,…...
wamp集成环境部署
Windows下Apache服务器搭建 第一步:下载Windows下的最新ZIP压缩包 推荐下载网址:http://www.apachelounge.com/download/ 为了让Apache服务器发挥更好的性能,请根据自己的系统选择下载,如果不清楚自己的系统是64位还是32位&am…...

使用antd design pro 及后端nodejs express 结合minio进行文件的上传和下载管理
使用Ant Design Pro前端框架结合Node.js Express后端服务以及MinIO作为对象存储,实现文件上传和下载管理的基本步骤如下: 1. 安装所需依赖 在Node.js Express项目中安装minio客户端库: npm install minio --save 在前端项目(假…...

Unity常用的优化技巧集锦
Unity性能优化是面试的时候经常被问道的一些内容,今天给大家分享一些常用的Unity的优化技巧和思路,方便大家遇到问题时候参考与学习。 对啦!这里有个游戏开发交流小组里面聚集了一帮热爱学习游戏的零基础小白,也有一些正在从事游…...

c++动态调用dll
在C中动态调用DLL(动态链接库)可以使用Windows API函数。以下是一个简单的示例,演示如何动态加载和调用DLL中的函数: #include <windows.h> #include <iostream>int main() { // 加载DLL HMODULE hModule LoadLibrar…...

使用Python自动化操作手机,自动执行常见任务,例如滑动手势、呼叫、发送短信等等
使用Python自动化操作手机,自动执行常见任务,例如滑动手势、呼叫、发送短信等等。 此自动化脚本将帮助你使用 Python 中的 Android 调试桥 (ADB) 自动化你的智能手机。下面我将展示如何自动执行常见任务,例如滑动手势、呼叫、发送短信等等。 您可以了解有关 ADB 的更多信息,…...

E - Souvenir(图论典型例题)
思路:对于有很多询问的题,一般都是先初始化。我们求出每个点到其他点的最短路径以及相同路径下最大的价值和即可。 代码: #include <bits/stdc.h> #define pb push_back #define a first #define b second using namespace std; type…...

【SpringBoot篇】添加富文本编辑器操作
文章目录 🍔使用步骤⭐首先我们需要安装富文本编辑器⭐在<script>中引入富文本编辑器⭐富文本图片上传接口⭐初始化富文本编辑器⭐调用 初始化富文本编辑器的方法🎈新增🎈编辑🎈保存 ⭐添加按钮⭐实现viewEditor函数&#x…...

前台vue配置
前台 vue环境 1.傻瓜式安装node: 官网下载:https://nodejs.org/zh-cn/2.安装cnpm: >: npm install -g cnpm --registryhttps://registry.npm.taobao.org3.安装vue最新脚手架: >: cnpm install -g vue/cli注:如果2、3步报错,清除缓…...

牛客周赛 Round 18 解题报告 | 珂学家 | 分类讨论计数 + 状态DP
前言 整体评价 前三题蛮简单的,T4是一个带状态的DP,这题如果用背包思路去解,不知道如何搞,感觉有点头痛。所以最后还是选择状态DP来求解。 欢迎关注 珂朵莉 牛客周赛专栏 珂朵莉 牛客小白月赛专栏 A. 游游的整数翻转 这题最好…...

CentOS防火墙基本操作
CentOS操作系统中的防火墙可以使用firewalld或iptables来进行配置。 firewalld(默认): 查看当前状态:systemctl status firewalld 开启/关闭防火墙服务:sudo systemctl start/stop firewalld 设置开机自动启动/不启…...

Shell脚本的编程规范和变量类型
一. 了解编程 1.程序编程风格 面向过程语言 开发的时候 需要一步一步执行 问题规模小,可以步骤化,按部就班处理 以指令为中心,数据服务于指令 C,shell 面向对象语言 开发的时候 将任务当成一个整体 将编程看成是一个…...
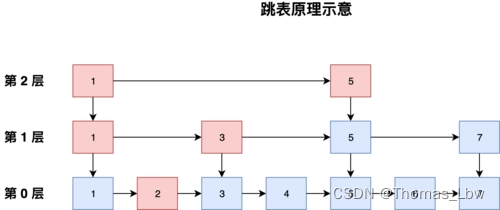
C++面试:跳表
目录 跳表介绍 跳表的特点: 跳表的应用场景: C 代码示例: 跳表的特性 跳表示例 总结 跳表(Skip List)是一种支持快速搜索、插入和删除的数据结构,具有相对简单的实现和较高的查询性能。下面是跳表…...

掌握C++20的革命性特性:Concepts
掌握C20的革命性特性:Concepts C20 的新特性 C20 引入了 Concepts,这是一种用于限制类和函数模板的模板类型和非类型参数的命名要求。Concepts 是作为编译时评估的谓词,用于验证传递给模板的模板参数。Concepts 的主要目的是使模板相关的编…...

win11开机后频繁刷新桌面,任务栏不显示,文件资源管理器explorer报错ntdll.dll
win11 开机后桌面频繁刷新,cpu 暴涨,任务栏不出现。 不知道是安装了什么软件还是系统升级造成的,好长时间不重启电脑了,然后重启了下电脑。 结果就是: 现象描述 重启后 输入密码进入后 变得巨慢。好久才进入的桌面。…...

解决Git添加.gitignore文件后不生效的问题
1. 问题描述 如上图所示,在已存在.gitignore文件且已经提交过的Git管理的项目中,其中.class、.jar文件以及.idea目录内的内容全部都还是被Git管理了,可见.gitignore文件并没有生效。 2. 原因发现 .gitignore文件只能作用于 Untracked Files…...

Shell Linux学习笔记
注意:该文章摘抄之百度,仅当做学习笔记供小白使用,若侵权请联系删除! 目录 什么是shell ? Linux正则匹配 grep tar与unzip echo history 重定向 shell 单双引号 位置参数 预定义变量 运算 正则表达式 字符截取命令 …...

kingbase常用SQL总结之锁等待信息
锁信息与等待事件 分析kingbase(pg)数据库锁等待、死锁时需要我们准确的定位等锁或者死锁相关的事务。关于获取锁等待信息或者死锁信息已有经典的SQL可以直接使用,但是需要我们先了解sql语句获取的每个字段的意义。 获取到锁等待事务不能完全…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
