三国游戏(第十四届蓝桥杯)
题目
小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵 X,Y,Z(一开始可以认为都为 0)。
游戏有 n个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第 i个事件发生时会分别让 X,Y,Z
增加 A i , B i , C i A_i,B_i,C_i Ai,Bi,Ci。
当游戏结束时 (所有事件的发生与否已经确定),如果 X,Y,Z的其中一个大于另外两个之和,我们认为其获胜。
例如,当 X>Y+Z时,我们认为魏国获胜。
小蓝想知道游戏结束时如果有其中一个国家获胜,最多发生了多少个事件?
如果不存在任何能让某国获胜的情况,请输出 −1。
输入格式
输入的第一行包含一个整数 n。
第二行包含 n个整数表示 A i A_i Ai,相邻整数之间使用一个空格分隔。
第三行包含 n个整数表示 B i B_i Bi,相邻整数之间使用一个空格分隔。
第四行包含 n 个整数表示 C i C_i Ci,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
数据范围
对于 40%的评测用例,n≤500;
对于 70%的评测用例,n≤5000;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 , 0 ≤ A i , B i , C i ≤ 1 0 9 1≤n≤10^5,0≤A_i,B_i,C_i≤10^9 1≤n≤105,0≤Ai,Bi,Ci≤109。
注意,蓝桥杯官方给出的关于 A i , B i , C i A_i,B_i,C_i Ai,Bi,Ci
的数据范围是 1 ≤ A i , B i , C i ≤ 1 0 9 1≤Ai,Bi,Ci≤10^9 1≤Ai,Bi,Ci≤109,但是这与给出的输入样例相矛盾,因此予以纠正。
输入样例:
3
1 2 2
2 3 2
1 0 7
输出样例:
2
样例解释
发生两个事件时,有两种不同的情况会出现获胜方。
发生 1,2 事件时蜀国获胜。
发生 1,3 事件时吴国获胜。
代码(python版本)
n=int(input())
def check(x,y,z)->int:w=[]for i in range(n):w.append(x[i]-y[i]-z[i])w.sort(reverse=True)res=-1sum=0for i in range(n):sum+=w[i]if sum>0:res=i+1return res
a=list(map(int,input().split()))
b=list(map(int,input().split()))
c=list(map(int,input().split()))
print(max(check(a,b,c),check(b,a,c),check(c,a,b)))
代码(cpp版本)
代码先欠着
思路:
本题是一道贪心题。当我一开始看这个题目的时候,首先想到的就是一道dfs题,但是当我看到数据范围为 1 0 5 10^5 105的时候我直接人傻,这还怎么dfs。于是换一个思路。
首先因为这个数据范围是 1 0 5 10^5 105,那么我们需要将时间复杂度控制在 n l o g n nlogn nlogn中。
本题要求的是一个国家打赢两个国家最多能发生多少次事件,看到最多,我就感觉是一道贪心题,那么怎么贪心呢?
首先我们需要想明白怎么贪?那我们可以先假设三个国家分别是ABC,然后我们假设 A > B + C A>B+C A>B+C,那么ABC到底是哪三个国家呢?这个直接可以枚举出来,A是魏蜀吴三个其中之一,剩下的B和C就是除了A以外的两个国家。
那么我们可以写一个函数来判断 A > B + C A>B+C A>B+C最多能要多少次
那么我们可以遍历ABC三个数组,然后用一个数组W来接受一下A国和B+C国的兵力差,也就是W[i]=A[i]-B[i]-C[i]的值,那么W[i]的含义是什么呢?很明显当W[i]>0的时候说明A的兵力比B+C的要多,这个事件我们当然要选。然后进行排序,接下来就是每次都获取到当前的兵力。然后用一个sum来记录,sum代表的是什么意思呢,就是A当前比B+C多sum个兵,然后我们依次进行遍历,sum不断累加W[i],当sum累加当前的兵力之后还是大于零,说明当前的事件容许发生,这时候就该让res++了。直到sum小于0的时候就不行了。
然后我们来看这个思路,整个的时间复杂度正好是 n l o g n nlogn nlogn(sort的时间复杂度)。
最后我们只需要调用上面的函数三次即可,也就是check(魏,蜀,吴),check(蜀,魏,吴),check(吴,蜀,魏),然后三者取最大值就行。
相关文章:
)
三国游戏(第十四届蓝桥杯)
题目 小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵 X,Y,Z(一开始可以认为都为 0)。 游戏有 n个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第 i个事件发生时会分别让 X,Y,Z 增加 A i , B…...
k8s---包管理器helm
内容预知 目录 内容预知 helm相关知识 Helm的简介与了解 helm的三个重要概念 helm的安装和使用 将软件包拖入master01上 使用 helm 安装 Chart 对chart的基本使用 查看chart信息 安装chart 对chart的基本管理 helm自定义模板 在镜像仓库中拉取chart,查…...
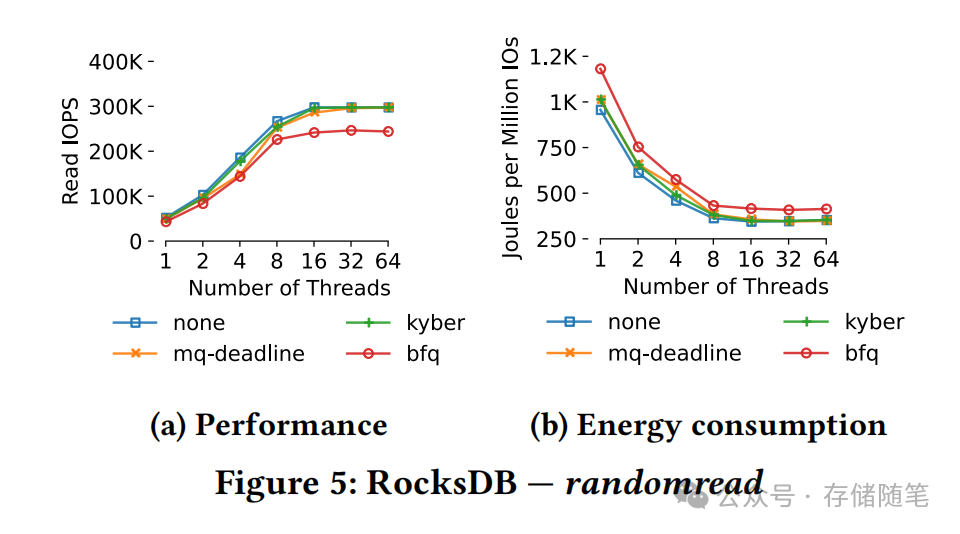
对于超低延迟SSD,IO调度器已经过时了吗?-part2
为了进行这项研究,他们设计了一套严谨的实验方法论,包括在配备了高速Intel Optane P4801X Series NVMe SSD的服务器上执行一系列微观和宏观基准测试,同时监测系统能耗情况。这些测试涵盖了多种工作负载场景,从单一进程提交大量请求…...

【C++】list的使用
目录 1 构造1.1 无参构造1.2 构造的list中包含n个值为val的元素1.3 用[first, last)区间中的元素构造list1.4 拷贝构造 2 迭代器的使用2.1 begin end2.2 rbegin rend 3 容量操作3.1 empty size 4 获取元素4.1 front back 5 插入、删除、修改5.1 头插-push_front和尾插-push…...
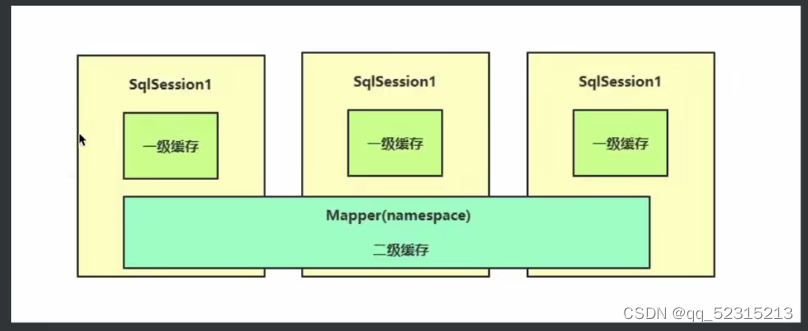
mybatis的缓存机制
视频教程_免费高速下载|百度网盘-分享无限制 (baidu.com) MyBatis 有一套灵活而强大的缓存机制,主要分为两级缓存:一级缓存(本地缓存)和二级缓存(全局缓存)。 一级缓存(本地缓存)&a…...

ChatGLM3报错:No chat template is defined for this tokenizer
使用官方提供的脚本创建ChatGLM3的DEMO: cd basic_demo python web_demo_gradio.py 出现效果异常问题: conversation [{role: user, content: 你好}, {role: assistant, content: 你好,有什么我可以帮助你的吗?\n\n<|im_end|…...

大数据学习之Flink、搞懂Flink的恢复策略
第一章、Flink的容错机制 第二章、Flink核心组件和工作原理 第三章、Flink的恢复策略 第四章、Flink容错机制的注意事项 第五章、Flink的容错机制与其他框架的容错机制相比较 目录 第三章、Flink的恢复策略 Ⅰ、恢复策略 1. Checkpoint: 2. Savepoint&#…...

C语言易忘操作符全集
目录 位操作符 1.按位与(&) 2.按位或(|) 3.按位异或(^) 4.按位取反(~) 5.左移(<<) 6.右移(>>) 逻辑操作符 1.逻辑与(&&) 2.逻辑或(||) 3.逻辑非(!) 位操作符 1.按位与(…...

网络请求 mvp mvvm get post delete put 请求
get 参数拼接 如下接口 localhost:8080/uav/plotting/page/app?pageNum1&pageSize10&appIde3c59e28-2032-4ddf-a762-7cec96f772a4&orgId65&plottingTypepoint GET("https:/uav/plotting/page/app") Observable<PlotList.DataBean> allPoin…...

研究生开题报告撰写:文言一心VSChatgpt3.5
文言一心 问:我是一名研二学生,请帮我生成一份研究生毕设开题答辩ppt框架。 答:好的,以下是一份研究生毕设开题答辩PPT的框架,供您参考: 幻灯片1:封面页 标题:研究生毕设开题答辩…...
Unity animator动画倒放的方法
在Unity中, 我们有时候不仅需要animator正放的效果,也需要倒放的效果。但我们在实际制作动画的时候可以只制作一个正放的动画,然后通过代码控制倒放。 实现方法其实很简单,只需要把animator动画的speed设置为-1即为倒放ÿ…...

Dubbo源码解析第一期:如何使用Netty4构建RPC
一、背景 早期学习和使用Dubbo的时候(那时候Dubbo还没成为Apache顶级项目),写过一些源码解读,但随着Dubbo发生了翻天覆地的变化,那些文章早已过时,所以现在计划针对最新的Apache Dubbo源码来进行“阅读理解…...
unity刷新grid,列表
获取UIGrid 组件,更新列表 listParent.GetComponent().repositionNow true;...

蓝桥杯备赛 day 3 —— 高精度(C/C++,零基础,配图)
目录 🌈前言: 📁 高精度的概念 📁 高精度加法和其模板 📁 高精度减法和其模板 📁 高精度乘法和其模板 📁 高精度除法和其模板 📁 总结 🌈前言: 这篇文…...

人形机器人创新发展顶层设计与关键技术布局
系列文章目录 前言 随着新一轮科技革命和产业变革的深入推进,我国高度重视人形机器人的创新发展,提出了一系列具有前瞻性和战略性的指导意见。规划指出,到2025年,我国将初步建立人形机器人创新体系,攻克“大脑”、“小…...

C语言-算法-最小生成树
【模板】最小生成树 题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 输入格式 第一行包含两个整数 N , M N,M N,M,表示该图共有 N N N 个结点和 M M M 条无向边。 接下来 M M M 行…...

android 扫描某个包下的所有类
注意事项 如果在用Android Studio开发过程中,如果新增了类,扫描不到。只能把APP卸载了,才能扫描到。 可能是Instance Run 的影响。 后面研究一下这篇文章,看看能不能解决 Android 遍历Apk下的所有类文件 package com.trs.nmip.…...

远程ssh 不通的原因之一
背景:我都想大喊一声,我上网是通的, ping网址是通的,ping www.baidu.com 是通的, 怎么都远程不了,报超时;嘿, 别人远程就能行。我都想挠头了。 目录 1. 先 ping 自己,…...
wamp集成环境部署
Windows下Apache服务器搭建 第一步:下载Windows下的最新ZIP压缩包 推荐下载网址:http://www.apachelounge.com/download/ 为了让Apache服务器发挥更好的性能,请根据自己的系统选择下载,如果不清楚自己的系统是64位还是32位&am…...

使用antd design pro 及后端nodejs express 结合minio进行文件的上传和下载管理
使用Ant Design Pro前端框架结合Node.js Express后端服务以及MinIO作为对象存储,实现文件上传和下载管理的基本步骤如下: 1. 安装所需依赖 在Node.js Express项目中安装minio客户端库: npm install minio --save 在前端项目(假…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
