【第十五课】数据结构:堆 (“堆”的介绍+主要操作 / acwing-838堆排序 / c++代码 )
目录
关于堆的一些知识的回顾
数据结构:堆的特点
"down" 和 "up":维护堆的性质
down
up
数据结构:堆的主要操作
acwing-838堆排序
代码如下
时间复杂度分析
确实是在写的过程中频繁回顾了很多关于树的知识,有关的文章都在专栏里,需要的可以去回顾一下~
http://t.csdnimg.cn/0d6Iq![]() http://t.csdnimg.cn/0d6Iq
http://t.csdnimg.cn/0d6Iq
关于堆的一些知识的回顾
关于堆,我的印象中是内存机制里的堆。之前写过的,在回顾一下吧~

然而我们这里说的堆,其实是一种用数据结构中的完全二叉树实现的堆。
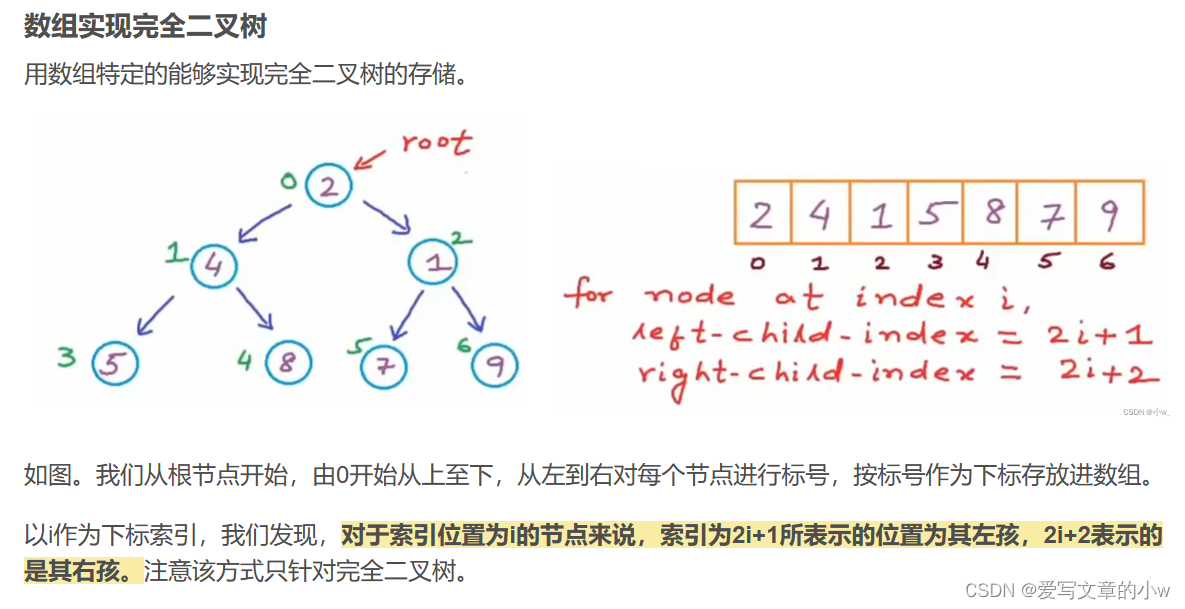
(我们这里图片上写的坐标索引方式是根节点从0开始索引,我们下面会采用下标从1开始索引,那样的话,左儿子就应该是2x 右儿子是2x+1 可以理解哈)
其实这里还要回顾一下树的广度优先遍历,即一层一层,从左到右的遍历方式,对于完全二叉树来说,其广度优先遍历就是创建一个数组,按照特定的存储方式进行存储,最终直接输出数组元素。对于其他的树,采取队列的存储方式。下面这篇文章详细介绍了树的遍历,也对数组存储有更深的解释,感兴趣可以看一下
http://t.csdnimg.cn/NngZ6
数据结构:堆的特点
1.完全二叉树的结构
堆是一个完全二叉树,这意味着除了最底层,其他层都是满的,而最底层的节点都集中在左侧。
到这里就要疑惑为什么堆是完全二叉树这种结构了
http://www.zhihu.com/question/36134980/answer/87490177
这篇文章作者详细解释了关于"堆"这种数据结构好处包括用途,我感觉写的非常不错,可以看一下加深理解。
其中主要提到:1.完全二叉树这种结构可以使用数组实现存储,并且便于索引。
2.它的出现是为了解决----对一个动态的序列进行排序,并且随时想知道这个序列的最小值或最大值
2.最小堆和最大堆
堆可以分为最小堆和最大堆两种类型。在最小堆中,每个节点的值都小于或等于其子节点的值。而在最大堆中,每个节点的值都大于或等于其子节点的值。(也叫小根堆和大根堆)
"down" 和 "up":维护堆的性质
"down" 操作通常涉及到将元素向下移动,适用于删除操作和堆化过程中。
通过 down(k) 进行下沉操作是为了调整以 k 为根的子树,确保其满足最小堆的性质。这主要关注了 k 节点向下的关系。
"up" 操作涉及到将元素向上移动,适用于插入操作和堆化过程中。
通过 up(k) 进行上浮操作是为了确保从删除元素的位置 k 开始,向上到根节点的路径上的每个父节点都满足最小堆的性质。这主要关注了 k 节点向上的关系。
而我们所说的 "down" 和 "up" 是通常用于--维护堆的性质。以确保堆的性质不被破坏。
下面以小根堆为例
down

根据这个思路我们写出代码
//调整以x为根的子树,以满足小根堆的性质(x是经过某种操作得到的值,在操作之前整棵树是满足堆的性质的)
void down(int x)
{int t=x;//t表示三个数中的最小值
//比较的前提都是孩子存在if(x*2<=size && he[x*2]<he[t])t=x*2;if(x*2+1<=size && he[x*2+1]<he[t])t=x*2+1;if(x!=t)//所以这里如果不需要交换位置,那说明更改的这个值并没有破坏原有的性质{swap(he[x],he[t]);down(t);//需要交换 说明我们又更改了一个位置的值,所以要继续判断这次更改的是否符合性质}
}down操作的前提就是 本身这个树的每个节点都是符合性质的,只是某一个值发生了改变,
我们针对这个发生改变的值,不管它是插入还是修改还是更改而导致的值的变化,我们最主要的就是关注改值之后,以其为根节点的子树。
将该值与它的原本的左右两个孩子的值的比较,如果不需要交换位置,说明这次的更改的值并没有引起堆的性质的变化
up
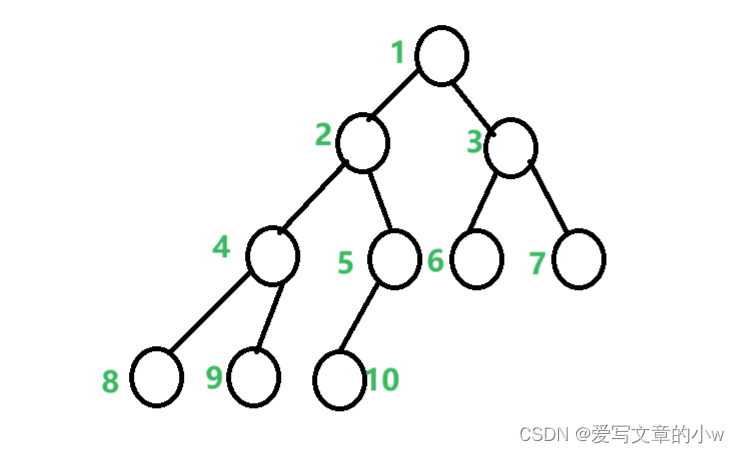
如上图这种完全二叉树,按照数组存储方式,观察其下标表示,我们发现孩子节点是其父节点下标的二倍。
由于小根堆的性质,根节点小于左右孩子,所以我们检查的时候只看该节点与根节点的大小关系就好了,因为另一个孩子一定是大于根节点且符合性质的。
void up(int x)
{while(x/2 && he[x/2]>he[x])//当该元素存在父节点且满足大小关系{swap(he[x/2],he[x]);x /= 2;//更新父节点}
}有了上面down的详细解释这个应该很容易理解了。
数据结构:堆的主要操作
1.插入一个元素,并仍保持堆的性质。
2.删除最小/大值。
3.堆化:将一个无序数组转换为堆,或者修复一个破坏了堆性质的堆。
这里先详细说一下堆化
for(int i=n/2;i;i--)down(i);我们通常从倒数第二层(n/2是最后一个元素的父节点)开始进行逐个元素下沉,最终达到将数组堆化的结果。 这是因为底层节点是叶子节点,它们自身已经满足堆的性质,不需要进行下沉操作。
 关于手写堆的一些主要操作就是上面这些。
关于手写堆的一些主要操作就是上面这些。
下面我逐个来解释。
1.插入一个数。由于我们堆结构是用数组实现存储的完全二叉树,因此对于数组来说,在末尾添加一个元素是很容易的,所以我们先把这个要插入的元素放到堆的末尾,在进行up操作,使其符合堆的性质。
2.求最小值,我们小根堆的根节点就是其最小值。
3.删除最小值。由于我们总是要删除一个元素的,在数组存储结构中,删除最后一个元素是很简单的,直接使我们使用到的下标--就行,但是我们要删的是第一个元素呀,怎么办呢?我们把最后一个元素的值标记覆盖到第一个元素的位置,再删除掉最后一个元素,再把刚刚放到第一位的元素进行down操作,使其符合堆的性质。
4.删除任意一个元素。在3思路的基础上,由于我们不清楚最后一个元素相较于原来这个位置上删除掉的元素是大还是小,如果是大于原来的元素,那就会执行down,如果小于,就会向上执行up,因此,这两个只会执行其中一个,为了简化代码,我们直接不判断,把两个都放上去。
5.修改任意一个元素,解释同4
acwing-838堆排序
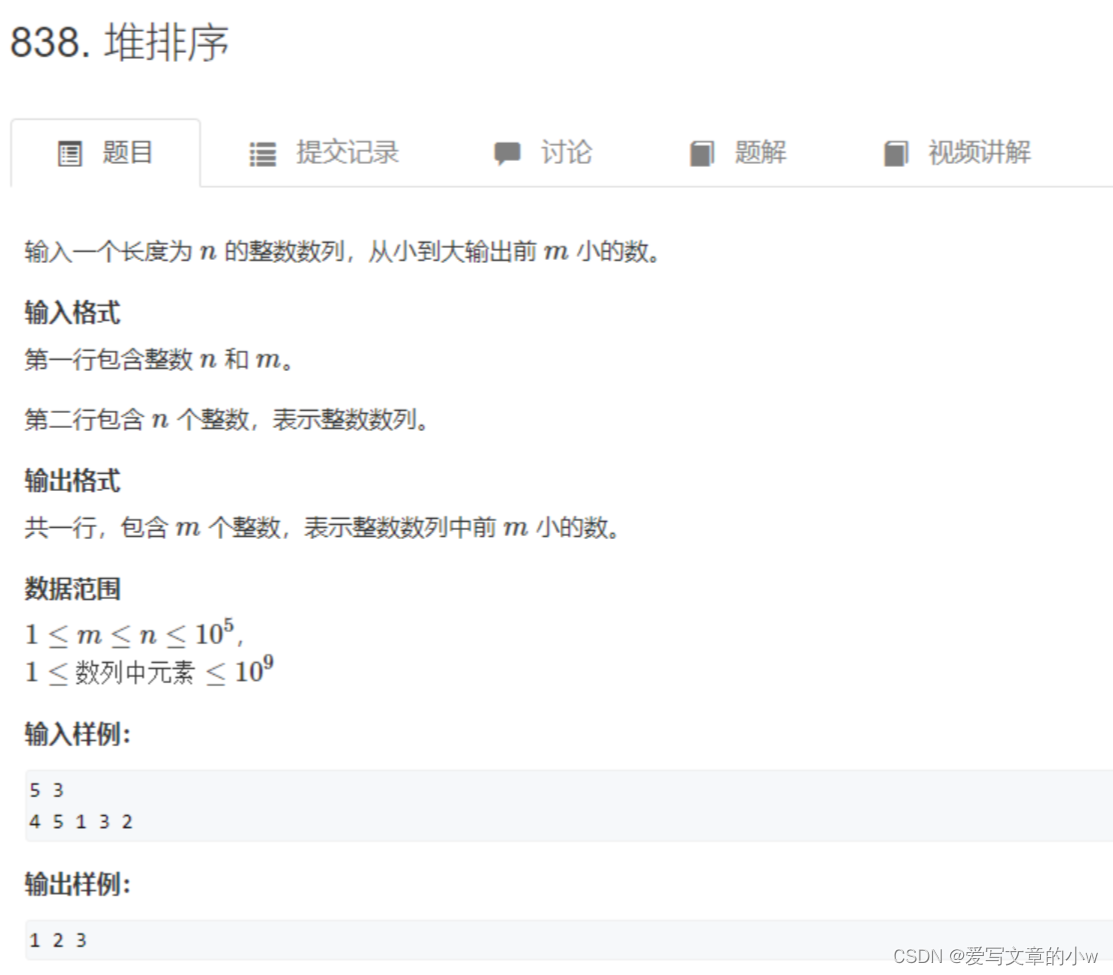
经过上面的介绍其实这道题的核心都已经解了,直接看代码把。
代码如下
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int n,m;
int he[N],size;//调整以 x 为根的子树,以满足小根堆的性质
void down(int x)
{int t=x;//t表示三个数中的最小值if(x*2<=size && he[x*2]<he[t])t=x*2;if(x*2+1<=size && he[x*2+1]<he[t])t=x*2+1;if(x!=t){swap(he[x],he[t]);down(t);}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&he[i]);}size=n;//size标记数组最后一个元素for(int i=n/2;i;i--)down(i);//将数组堆化while(m--)//每次输出一个最小值{printf("%d ",he[1]);he[1]=he[size];//删除最小值size--;down(1);}return 0;
}时间复杂度分析
在这段代码中:
①输入数据的for循环O(n)
②建堆的for循环,先看down函数,down是逐层比较,其时间复杂度取决于树的高度,所以最坏情况下就是该二叉树为满二叉树时的树高,即log(n)。那么真整个建堆过程时间复杂度应为O(n*log(n))
--关于这里的时间复杂度其实还有一种思考方式,等之后回来补写一下。
③输出最小值的while循环,也是取决于down函数执行次数,即O(m*log(n))
哎,就差一个模拟堆(烦躁),是有点强迫症在的😢明天在写啦。。
有问题欢迎指出!一起加油!!
相关文章:

【第十五课】数据结构:堆 (“堆”的介绍+主要操作 / acwing-838堆排序 / c++代码 )
目录 关于堆的一些知识的回顾 数据结构:堆的特点 "down" 和 "up":维护堆的性质 down up 数据结构:堆的主要操作 acwing-838堆排序 代码如下 时间复杂度分析 确实是在写的过程中频繁回顾了很多关于树的知识&…...

前端JavaScript篇之JavaScript有哪些数据类型,它们的区别?
目录 JavaScript有哪些数据类型,它们的区别?数据类型区别 JavaScript有哪些数据类型,它们的区别? 数据类型 JavaScript数据类型有: Undefined、Null、Boolean、Number、String、Array、Object、Symbol、BigInt… St…...

LeetCode---380周赛
题目列表 3005. 最大频率元素计数 3006. 找出数组中的美丽下标 I 3007. 价值和小于等于 K 的最大数字 3008. 找出数组中的美丽下标 II 一、最大频率元素计数 这题就是个简单的计数题,正常遍历统计数据即可,关键是你要会写代码逻辑。 代码如下&…...

archlinux 如何解决安装以后没有声音的问题
今天安装完archlinux以后发现看视频没声音 检查一下是否有 /lib/firmware/intel/sof 发现没有 如果你也是这样的话,可以尝试安装: sudo pacman -S sof-firmware 重启后再看看有没有声音: reboot 反正我有声音了...

什么是ORM思想?
1. ORM概念 ORM(Object Relational Mapping)对象关系映射模式,是一种技术,解决了面向对象与关系型数据库存互不匹配的现象。 ORM在业务逻辑层和数据库层之间充当了桥梁的作用。 2. ORM由来 在软件开发的过程中,通常…...

设计接口时,为其添加签名鉴权---详细教程
一、何为签名 我们知道无论是restful api还是传统接口、亦或是其他形式接口的调用,接口签名都是非常重要的安全机制,它可以确保请求的发起者是经过认证和授权的客户端,同时也可以防止接口被攻击,请求参数被篡改等等。 用大白话来解…...
5G+物联网:连接万物,重塑智慧社区,开启未来生活新纪元,助力智慧社区的革新与发展
一、5G与物联网:技术概述与基础 随着科技的飞速发展,第五代移动通信技术(5G)和物联网(IoT)已经成为当今社会的热门话题。这两项技术作为现代信息社会的核心基础设施,正深刻地改变着人们的生活和…...
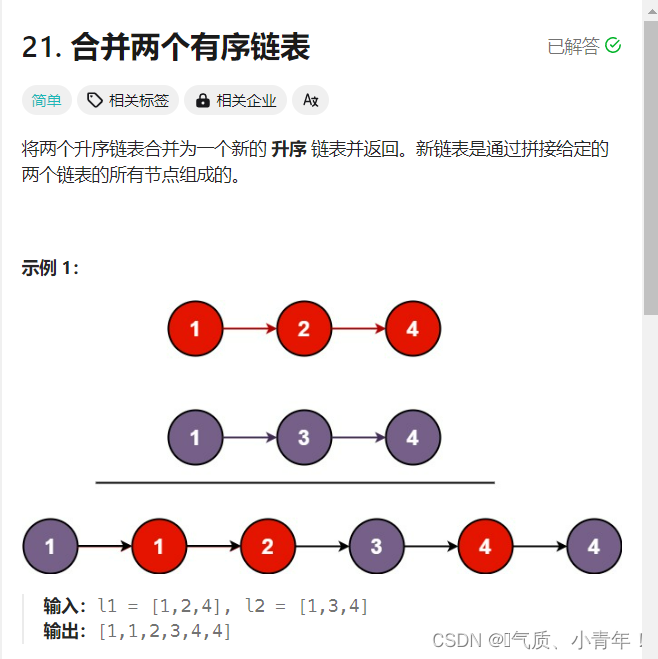
[反转链表] [合并两个有序链表][分割链表]
这里写目录标题 反转链表合并两个有序链表分割链表 反转链表 1、题目: 2.思路 思路1:建立一个newHead,取一个节点进行头插。具体做法如下! 建立一个newHead(新头),由于一个节点里面存的是下一个节点的地址,如果取…...
中文数据让LLM变笨?
我这里先贴一下论文的原链接: https://arxiv.org/abs/2401.10286 然后贴一下我翻译标注的下载链接:https://gitee.com/chatpaper/arXiv_top_chinese/blob/master/0801_top/%E4%B8%AD%E6%96%87%E4%BC%9A%E8%AE%A9LLM%E5%8F%98%E7%AC%A8%EF%BC%9F.pdf 先…...
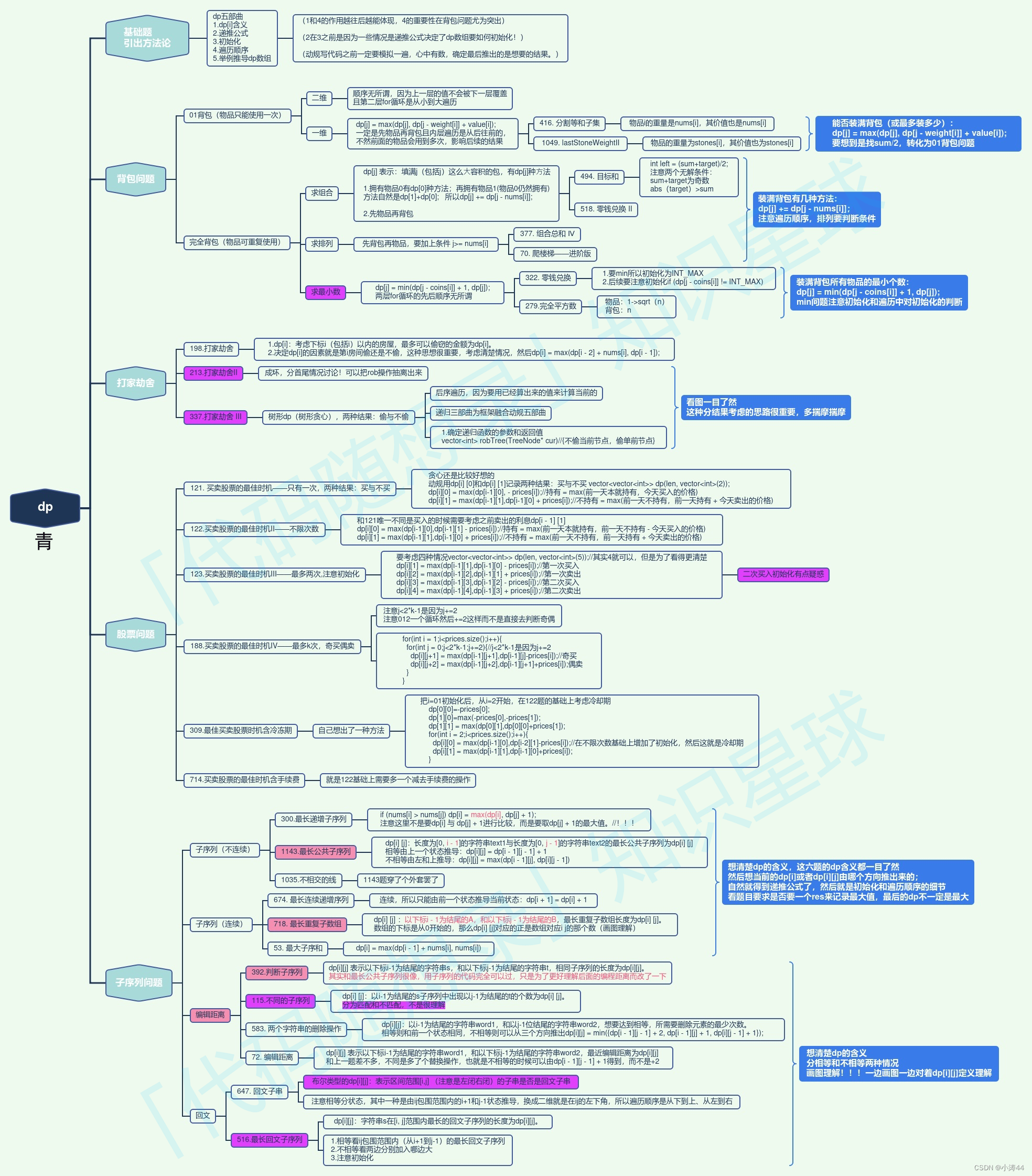
【代码随想录】刷题笔记Day54
前言 差单调栈就结束代码随想录一刷啦,回家二刷打算改用python补充进博客,小涛加油!!! 647. 回文子串 - 力扣(LeetCode) 双指针法 中心点外扩,注意中心点可能有一个元素可能有两个…...
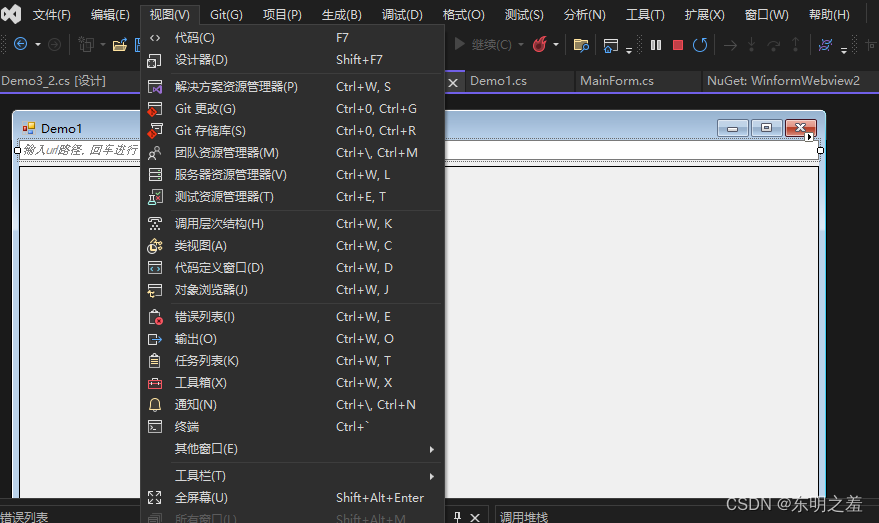
二.Winform使用Webview2在Demo1中实现地址简单校验
Winform使用Webview2在Demo1中实现地址简单校验 往期目录回顾添加对于的简单url验证提示通过上节和本节涉及到的函数有 往期目录 往期相关文章目录 专栏目录 回顾 通过一.Winform使用Webview2(Edge浏览器核心) 创建demo(Demo1)实现回车导航到指定地址 我们已经知道了解决资源…...

从0开始学习C++ 第二十课:模板与泛型编程
第二十课:模板与泛型编程 学习目标: 掌握模板的基本语法和概念。学会使用函数模板来创建可重用的函数。学习如何定义类模板以实现数据结构的泛型。理解模板在C中提供的灵活性和强大功能。 学习内容: 模板的概念: 模板是C中支持…...

pcl之滤波器(一)
pcl滤波器 pcl一共是有十二个主要模块,详细了解可以查看官网。https://pcl.readthedocs.io/projects/tutorials/en/latest/#basic-usage 今天学习一下pcl的滤波器模块。 滤波器模块,官网一共是提供了6个例程,今天先来看第一第二个。 直通…...
)
java项目性能优化(MyBatis中开启查询缓存及flushCache与useCache的使用)
在java项目中,如果需要大量的DB查询,导致缓存过多,项目运行缓慢,可以设置在select查询时,添加二级缓存的清空。 如果没有去配置flushCache、useCache,那么默认是启用缓存的。 1,flushCache默认…...
Unity3D控制人物移动的多种方法
系列文章目录 unity知识点 文章目录 系列文章目录前言一、人物移动之键盘移动1-1、代码如下1-2、效果 二、人物移动之跟随鼠标点击移动2-1、代码如下2-2、效果 三、人物移动之刚体移动3-1、代码如下3-2、效果 四、人物移动之第一人称控制器移动4-1、代码如下4-2、效果 五、And…...

无人机打击激光器
激光器的应用非常广泛,涵盖了多个领域。以下是一些主要的激光器应用: 医疗领域:激光器在医疗行业中有着重要应用,比如用于激光手术(如眼科手术)、皮肤治疗、牙科治疗、肿瘤治疗等。 工业制造:在…...

Lingo数学建模基础
1.基本运算符 1.1算数运算符 1.2逻辑运算 #not# 否定操作数的逻辑值,一元运算符 #eq# 若两运算数相等,则为true,否则为false #ne# 若两运算数不相等,则为true,否则为false #gt# 若左边运算数严格大于右边,则为true,否则为…...
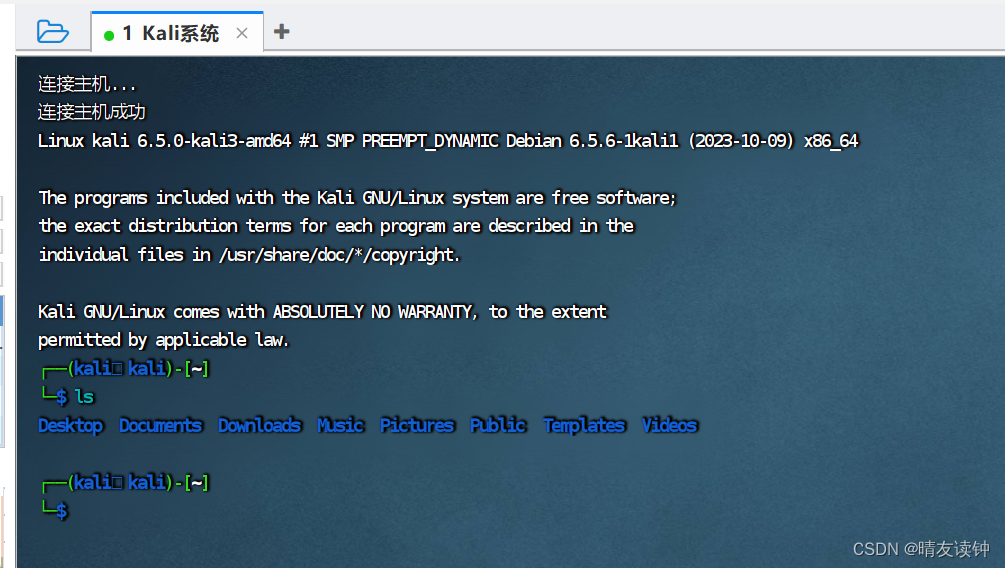
finalshell连接linux的kali系统
kali的ssh服务似乎是默认关闭的,笔者在玩CentOS系统时可以直接用finalshell完成连接,但kali不行,需要先手动开启ssh服务。 开启kali的ssh服务 输入【ssh start】命令开启ssh服务,可以用【ssh status】命令查看ssh状态,…...

2、Line Charts折线图
可视化时间趋势 现在你已经熟悉了编码环境,是时候学习如何制作自己的图表了! 在本教程中,您将学习足够的Python来创建专业外观的折线图。然后,在接下来的练习中,您将使用您的最新技能处理真实世界的数据集。 本课程数据集夸克网盘下载链接:https://pan.quark.cn/s/a235ac…...
)
shell脚本获得所有数据库备份(整库备份,表级备份)
数据库备份到天翼云对象存储OBS https://blog.csdn.net/qq_34631220/article/details/135755894 1、获得所有数据库 #!/bin/sh HOSTNAME"ip" #数据库信息 PORT"3306" USERNAME"root" PASSWORD"" DBNAME"yusuan" #数据库…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
