《计算机系统基础》—— 运算
文章目录
- 《计算机系统基础》——运算
- 整数
- 按位运算
- 作用
- 操作
- 位移运算
- 作用
- 操作
- 乘法运算
- 除法运算
- 浮点数
- 加减运算
- 乘除运算
《计算机系统基础》——运算
🚀🚀本章我们需要介绍的是有关C语言里面的运算,当然了,我们不会是介绍简单的运算,而是详细地介绍一下我们在日常开发中进行运算时可能遇到的问题。好了就让我们开始今天的学习吧!
整数
按位运算
作用
🚀🚀按位运算在我们日常的开发中出现的比较少,他的作用主要就是对位串实现“掩码”(mask)操作或相应的其他处理,比如在嵌入式领域一般用来控制寄存器的值,以达到相应的功能。
操作
- 按位或:“|”
- 按位与:“&”
- 按位取反:“~”
- 按位异或:“^”
🚀🚀比如用下面的语句用“&”实现“掩码”操作,作用为从数据y中提取低位字节,并使高字节为0。
y & 0x00FF
位移运算
🚀🚀一提到移位操作,很多人就是觉得只是用来乘除2的,但是事情并没有那么简单,接下来我们来详细的介绍一下。
作用
🚀🚀位移运算在我们的日常开发中一般都是用来乘除2的,但是它不仅仅只有这一个功能,除此之外,它还可以提取部分信息。
操作
- 左移: x<<k(乘2)
- 右移: x>>k(除2)
- 逻辑右移:在左边补k个0
- 算数右移:在左边补k个最高位的有效数字
🚀🚀我们在下方给出关于逻辑右移和算数右移的例子来帮助大家理解。
| 操作 | 值1 | 值2 |
|---|---|---|
| 参数x | [01100011] | [10010101] |
| x << 4 | [00110000] | [01010000] |
| x >> 4(逻辑右移) | [00000110] | [00001001] |
| x >> 4(算数运算) | [00000110] | [11111001] |
🚀🚀如果位移数大于数据位数怎么办呢?答案很简单,会对数据取余,比如对32位数据右移36位,其实就是右移4位。
乘法运算
🚀🚀在高级语言中,两个n位整数相乘得到的结果通常也是 一个n位整数,也即结果只取2n位乘积中的低n位。
🚀🚀比如:0101 * 0101 = 00011001,我们只取后4位,得到1001,经过换算,结果应该是-111,也就是-7,显然与我们想要得到的数字明显不一样。
🚀🚀那我们有没有什么办法去判断我们的结果是否是正确的呢?或者说,到底什么情况下结果不会溢出?答案是肯定的,我们接下来就来介绍一下。
🚀🚀判断我们最后的结果是正确的,我们可以使用下面的语句去判断:
当 !x || z/x==y 为真时
🚀🚀然后当我们的结果在:-2n-1 ≤ x*y < 2n-1 时,结果是不会溢出的,其实也就是:乘积的高n+1位为全0或全1,这样的结果就是正确的。
🚀🚀整数乘法运算比移位和加法等运算所用时间长,因此,编译器在处理变量与常数相乘时,往往以移位、加法和减法的组合运算来代替乘法运算,所以我们可以使用位移来代替乘法指令,比如x * 20,因为20 = 16 + 20 = 24 + 22 ,所以我们可以转换为(x<<4)+(x<<2)。
除法运算
🚀🚀除法运算和乘法运算其实是类似的,但是只有带符号整数进行**-2n-1/-1 = 2n-1**操作会发生溢出之外,其他都不会溢出,因为2n-1无法用n位来表示。
#include<stdio.h>void main ()
{int u = 0x80000000; printf ("u = %x = %x = %d\n", u , u / -1, u / -1);
}
🚀🚀运行结果如下所示:u = 80000000 = 80000000 = -2147483648,我们可以看到,在16进制下,u和u / -1 的结果是一样的。
🚀🚀除法运算的商为整数,于是如何进行取整就很重要了,我们只需要记住一个原则,就是按照朝0的方向舍入。即正数商取比自身小的最接近整数,负数商取比自身大的最接近整数。
🚀🚀同样的,为了缩短除法运算的时间我们可以采用右移运算来实现。如果能整除,我们就直接右移,如果不能整除,我们就可以加一个偏移量(2k -1),再右移即可,接下来我们就来介绍一下。
14/4 = 3 ; 0000 1110 >> 2 = 0000 0011
-14/4 = 1111 0010 + 0000 0011 ;1111 0101 >> 2 = 1111 1101 = -3
浮点数
🚀🚀对于浮点数,我们就不做过多的介绍,简单介绍一下运算以及其异常,但是浮点运算涉及的精度以及异常是非常重要的,有机会以后可以单独介绍一下,
加减运算
🚀🚀对于浮点数的加减运算,我们只需要注意,他是先对齐阶码,再进行运算,如下所示:
A ± B = (Ma + Mb* 2-(Ea-Eb)) * 2Ea (假设Ea>=Eb )
🚀🚀需要注意的就是,当我们的尾数高位为0,则需左规:尾数左移一次,阶码减1,直到MSB为1。当尾数最高位有进位,需右规:尾数右移一次,阶码加1,直到MSB为1。
乘除运算
🚀🚀乘除运算就需要注意阶码上溢(一个正指数超过了最大允许值)和下溢(一个负指数超过了最小允许值)的问题。过多的就不再介绍了,感兴趣的同学可以自行去查找资料。
相关文章:

《计算机系统基础》—— 运算
文章目录《计算机系统基础》——运算整数按位运算作用操作位移运算作用操作乘法运算除法运算浮点数加减运算乘除运算《计算机系统基础》——运算 🚀🚀本章我们需要介绍的是有关C语言里面的运算,当然了,我们不会是介绍简单的运算&…...

MSTP多进程讲解与实验配置
目录 MSTP多进程 专业术语 MSTP多进程配置 在MSTP域配置 MSTP多进程 多进程的作用 将设备上的端口绑定到不同的进程中,以进程为单位进行MSTP计算,不在同一进程内的端口不参与此进程中的MSTP协议计算,实现各个进程之间的生成树计算相互独立…...

【Python】软件测试必备:了解 fixture 在自动化测试中的重要作用
在自动化软件测试中,fixture 是一种确保测试在一致且受控条件下运行的重要方法。简单来说,fixture 就是一组先决条件或固定状态,必须在运行一组测试之前建立。在测试框架中,fixture 提供了一种方便的方法,用于在每个测…...

DevExpress皮肤引用的办法
1.引用Dll皮肤文件Typeprocedure SetSkin(skinnam:string);procedure TFrmMain.SetSkin(skinnam:string);varHinst:THANDLE;RStream:TResourceStream;beginHinst:Loadlibrary(ALLSK.dll);If Hinst0 ThenExitelsebeginRstream:TResourceStream.Create(Hinst,skinnam,MYSKIN);dxS…...

2023-03-04 区分纳米颗粒核壳原子
声明:未经允许,不得擅自复制、转载。欢迎引用:Laser-Assisted Synthesis of Bi-Decorated Pt Aerogel for Efficient Methanol Oxidation ElectrocatalysisApplied Surface Science ( IF 6.707 ) Pub Date : 2022-04-01 , DOI: 10.1016/j.aps…...

review设备管理
目录 1、设备管理基础知识 (1)、外部设备分类 (2)、注意事项 2、I/O硬件原理 (1)、不同方式对I/O设备分类 (2)、I/O控制方式 (3)、设备控制器 3、I/O软…...
详解)
Cadence Allegro 导出Bill of Material Report (Condensed)详解
⏪《上一篇》 🏡《总目录》 ⏩《下一篇》 目录 1,概述2,Bill of Material Report (Condensed)作用3,Bill of Material Report (Condensed)示例4,Bill of Material Report (Condensed)导出方法4.1,方法14.2,方法2,...

B. Sherlock and his girlfriend
Sherlock has a new girlfriend (so unlike him!). Valentines day is coming and he wants to gift her some jewelry. He bought n pieces of jewelry. The i-th piece has price equal to i 1, that is, the prices of the jewelry are 2, 3, 4, ... n 1. Watson…...

Spring SpEL表达式
Java知识点总结:想看的可以从这里进入 目录17、Spring SpEL17.1、简介17.2、配合value使用17.2.1、基本字面值17.2.2、类相关表达式17.2.3、properties17.2.4、T运算符17.2.5、new17.2.6、Elvis运算符17.2.7、运算符17.2、配合XML使用17、Spring SpEL 17.1、简介 S…...

Nginx反向代理原理详解与配置
Nginx反向代理是一种常用的反向代理技术,它允许您将一个或多个Web服务器上的内容公开给Internet上的客户端,而不必暴露您的服务器的IP地址。Nginx反向代理的原理是:客户端发出一个HTTP请求,Nginx服务器收到请求后,将请…...

Happen-Before从入门到踹门
什么是Happen-Before有人翻译为"先行发生原则",其实也没错,但是更准确的说法应该是,前一个操作的值,后一个总能察觉到。Happen-Before的八条规则程序有序性:在前面的代码优先于在后面的代码执行volatile的变…...

电力系统系统潮流分析【IEEE 57 节点】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
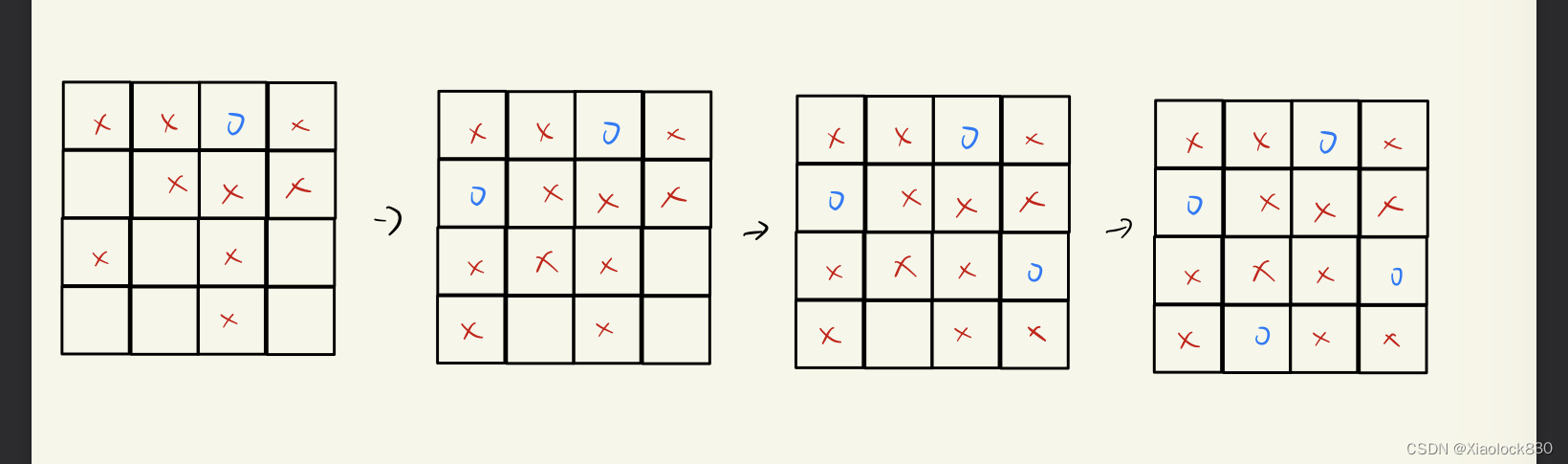
Java——N皇后问题
题目链接 leetcode在线oj题——N皇后 题目描述 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ÿ…...
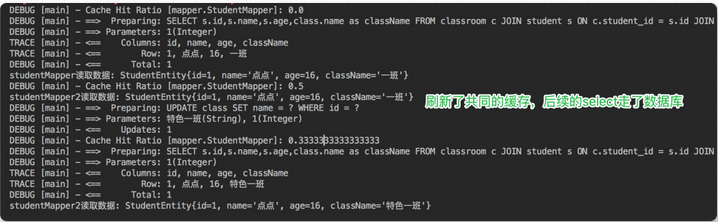
Mybatis一级缓存与二级缓存
一、MyBatis 缓存缓存就是内存中的数据,常常来自对数据库查询结果的保存。使用缓存,我们可以避免频繁与数据库进行交互,从而提高响应速度。MyBatis 也提供了对缓存的支持,分为一级缓存和二级缓存,来看下下面这张图&…...
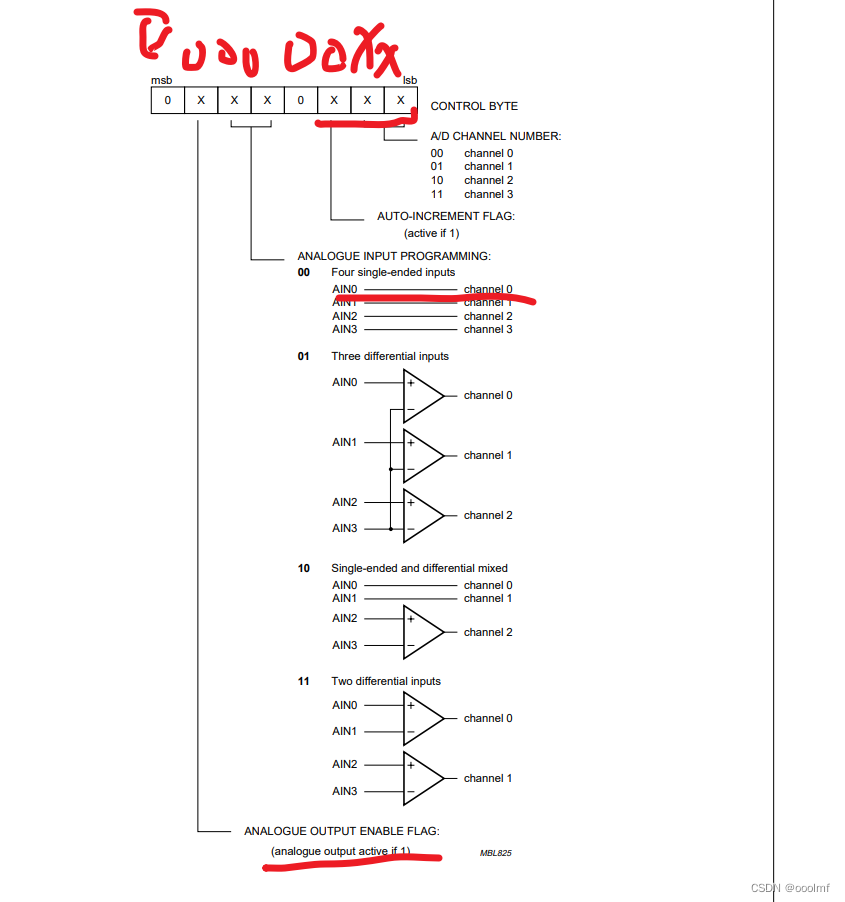
LQB,手打,PCF8591,ADDA转换,AD1是光敏电阻,AD3是电位器,DA输出
在上述at24c02de 基础上,添加三个函数 一个是读取通道1光敏电阻的数据; 一个是读取通道3的电压; 一个是输出DA的数据。。 5V的AD DA。 如果读入的电压是5V,输入AD,就是255; 如果是0V,就是00000…...

【计组笔记06】计算机组成与原理之控制器和总线结构
这篇文章,主要介绍计算机组成与原理之控制器和总线结构。 目录 一、控制器功能 1.1、控制器组成 1.2、控制单元的输入和输出...

elisp简单实例: auto-save
elisp 能找一个简单又实用的代码很不容易,以下代码不是我的原创,只是结合自己的理解,添加修正了一些注释,荣誉归原作者,感谢原作者的开源精神! 调用说明: 把后面代码存为auto-save.el 在init.el 中写上 (require auto-save) 就可以了. 下面是auto-save.el 内容了. ;; 我…...

写字楼/园区/购物中心空置率太高?快用快鲸智慧楼宇系统
客户租不租你的写字楼,事关区位、交通、环境、价格、面积、装修等诸多因素,但很多招商部对这些影响客户决策的数据并不重视,在客户初次上门看房时仅简单记录姓名、联系方式、需求面积,对其他核心数据熟视无睹,也为日后…...
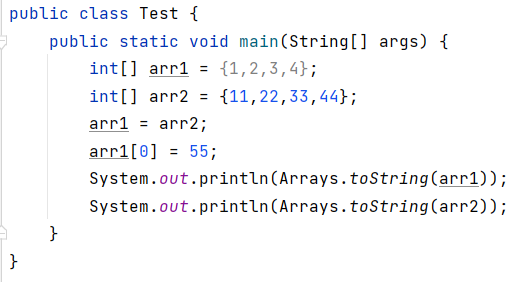
【JavaSE】数组的定义和使用(上)
数组的定义和使用(上)6-数组的定义与使用1. 数组的基本概念1.1 为什么要使用数组1.2 什么是数组1.3 数组的创建及初始化1.3.1 数组的创建1.3.2 数组的初始化1.4 数组的使用1.4.1 数组中元素的访问1.4.2 遍历数组2. 数组是引用类型2.1 初始JVM的内存分布2…...

计算机的学习路线
本文是介绍如何成为一个Geek,一个真正的计算机高手。 适合有成为IT领域技术大牛的人参考。 写给大一新生和所有向深耕IT领域的人,避免走一些弯路。 第一门入门的必备功课-语法与算法 什么是计算机? 用来做运算的机器 电子计算机在运算方面…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
