c递归算法模型
使用递归算法模型可以较为自然地解决许多问题,尤其是对于那些数据结构层次比较清晰的问题,递归算法模型往往能够提供一种简单清晰的解法。
递归算法模型的核心思想是将一个大问题通过递归的方式拆分为若干个较小的问题,并不断递归下去直到问题变得足够简单,直接求解即可。这个思想实质上也是分治思想的一种应用,将大问题分解为若干个子问题,进而得到子问题的解,最后将子问题的解整合起来得到原问题的解。
但是在使用递归算法模型时也需要注意一些细节问题。以下是一些需要注意的事项:
1. 定义好递归函数的边界条件,避免递归进入无限循环,导致程序崩溃或者降低程序执行效率。
2. 在递归函数中尽可能不要使用全局变量,要使用参数传递的方法来传递函数所需的数据。
3. 递归算法模型的实现过程中如果存在大量计算,则很容易产生栈溢出,因此在使用递归算法模型时需要尽量避免出现超长递归链的情况。
4. 在递归过程中如果需要开辟新的内存空间,则需要注意内存泄漏问题,及时释放不需要的内存空间,避免程序长时间执行后内存溢出。
5. 在递归过程中如果需要访问外部数据结构,一定要注意访问的合法性,避免出现访问越界等错误。
6. 在递归过程中尽量避免使用递归调用层数过多的方式,可以通过设计合理的算法减少递归层数,提高效率。
7. 对于非线性的数据结构(如树、图等),递归算法模型非常适合,但是需要注意一些特殊情况,如避免形成环路等。
总之,递归算法模型能够很好地解决许多问题,但是需要注意细节问题,避免程序出现异常情况,从而实现高效稳定的程序执行。
// n个数阶乘
#include <stdio.h>int fun(int n)
{// 递归终止条件if (n <= 1){return 1;} else {return n * fun(n - 1);}}int main()
{int sum = fun(5);printf("n! = %d\n", sum);return 0;
}
// 递归问题——汉诺塔
#include<stdio.h>
int count = 0;
// 在汉诺塔问题中,每次只能移动一个圆盘
// 初始状态下最上边的圆盘编号是1,最底层的圆盘编号是n
// 每次递归调用时,需要将目标柱子和借助柱子的顺序调换,以便于完成移动
// 将n个圆盘从a借助b移到c
void hanoi(int n, char a, char b, char c)
{// 递归终止条件if (n == 1)// 移动操作printf("00 第 %-3d 次: %c --> %c\n", ++count, a, c);else{// 移动n-1个圆盘时,需要将这些圆盘从柱子a移动到柱子b,此时柱子c可以作为借助的柱子// 因此,需要将顺序调整为acbhanoi(n - 1, a, c, b);// 当移动晚n-1圆盘后,需要将最后一个圆盘从柱子a移动到柱子c// 因此需要输出一条指令,将圆盘a移动到圆盘c// 移动操作printf("01 第 %-3d 次: %c --> %c\n", ++count, a, c);// 然后,需要将n-1个圆盘从柱子b移动到柱子c,此时,柱子a可以作为借助的柱子// 因此,需要将顺序调整为bachanoi(n - 1, b, a, c);}
}int main()
{int n = 0;printf("请输入汉诺塔层数:");scanf("%d", &n);hanoi(n, 'a', 'b', 'c');printf("共移动了%d次\n", count);return 0;
}// 斐波拉契数列是由一系列数字组成的序列。
// 该序列中的每一项都是前两项的和,起始项为0和1,第三项为1。
// 斐波拉契数列的前几个数字为:0,1,1,2,3,5,8,13,21,34,55,89,144,...
// 理解斐波拉契数列的方法有许多,其中一个常见的方法是通过兔子繁殖问题。
// 假设有一对新生的兔子,从第三个月开始,每对兔子每月可以繁殖一次,每次繁殖一对兔子。
// 第一个月新生的兔子还太小,不会繁殖,第二个月开始才开始繁殖。
// 设第 $n$ 个月时有 $F(n)$ 对兔子,则 $F(1)=F(2)=1$,当 $n>2$ 时,$F(n)=F(n-1)+F(n-2)$。// 在代码中我们用递归方式来求解斐波拉契数列。
// 函数的输入为要求的斐波拉契数列的前 $n$ 项,返回值为第 $n$ 项的数值。由于斐波拉契数列的定义中已经规定了前两项为 1 和 1,递归函数中的边界条件
// 即为当 $n<=1$ 时,返回 $n$。在递归调用的过程中,将求解 $n-1$ 项和 $n-2$项的函数值相加即可得到第 $n$ 项的数值。
// 我们在main函数中,通过循环依次输出前 $n$ 项的斐波拉契数列的值。比如当 $n=10$ 时,输出为:0,1,1,2,3,5,8,13,21,34。
// 需要注意的是,递归方式虽然简单,但是其时间复杂度较大,会出现较多重复计算的情况,因此计算高阶项时会比较慢。为了提高效率,可以使用非递归的方式实现斐波拉契数列的求解。#include <stdio.h>int fibonacci(int n)
{if (n <= 1) {return n;}return fibonacci(n-1) + fibonacci(n-2);
}int main()
{int n = 10;for (int i = 0; i < n; i++) {printf("%d ", fibonacci(i));}printf("\n");return 0;
}// 迷宫问题
#include <stdio.h>#define ROW 5
#define COL 5int maze[ROW][COL] = {{0, 1, 0, 0, 0},{0, 1, 0, 1, 0},{0, 0, 0, 0, 0},{0, 1, 1, 1, 0},{0, 0, 0, 1, 0},
};// 标记是否已经访问过
int visited[ROW][COL] = {0};int findPath(int i, int j)
{// 判断是否越界,如果是则返回0,表示该路径不可行if (i < 0 || i >= ROW || j >= COL){return 0;}// 判断是否是障碍物或者已经访问过if (maze[i][j] == 1 || visited[i][j] == 1){return 0;}// 到达终点返回1,表示找到了一条可行路径if (i == ROW - 1 && j == COL - 1){visited[i][j] = 1;return 1;}// 如果当前位置不是终点,就标记为已经访问,然后递归调用findPath,分别向上下左右4个方向寻找路径visited[i][j] = 1;if (findPath(i+1, j) || findPath(i-1, j) || findPath(i, j-1) || findPath(i, j+1)){return 1;}// 如果4个方向都没有找到可行路径,就将当前位置标记为为访问,返回0visited[i][j] = 0;return 0;
}int main()
{// 调用if (findPath(0, 0)) {printf("找到路径!\n");} else {printf("没有找到路径。\n");}return 0;
}
相关文章:

c递归算法模型
使用递归算法模型可以较为自然地解决许多问题,尤其是对于那些数据结构层次比较清晰的问题,递归算法模型往往能够提供一种简单清晰的解法。 递归算法模型的核心思想是将一个大问题通过递归的方式拆分为若干个较小的问题,并不断递归下去直到问…...

力扣740. 删除并获得点数
动态规划 思路: 选择元素 x,获得其点数,删除 x 1 和 x - 1,则其他的 x 的点数也会被获得;可以将数组转换成一个有序 map,key 为 x, value 为对应所有 x 的和;则问题转换成了不能同…...

spring和springboot的区别
在当今的软件开发领域,Spring和Spring Boot无疑是Java开发者最常用的框架之一。尽管它们都源于Spring项目,但它们在设计和使用上有很大的不同。本文将深入探讨Spring和Spring Boot之间的主要区别,以及为什么有时候选择其中一个而不是另一个是…...

imgaug库图像增强指南(35):【iaa.Fog】——轻松创建自然雾气场景
引言 在深度学习和计算机视觉的世界里,数据是模型训练的基石,其质量与数量直接影响着模型的性能。然而,获取大量高质量的标注数据往往需要耗费大量的时间和资源。正因如此,数据增强技术应运而生,成为了解决这一问题的…...
网络安全--防御保护02
第二天重要的一个点是区域这个概念 防火墙的主要职责在于控制和防护---安全策略---防火墙可以根据安全策略来抓取流量之后做出对应的动作 防火墙的分类: 单一主机防火墙:专门有设备作为防火墙 路由集成:核心设备,可流量转发 分…...
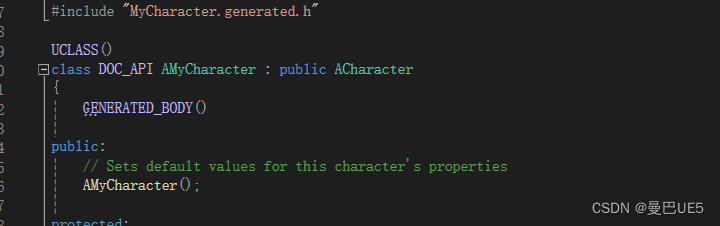
UE5 C++学习笔记 常用宏的再次理解
1.随意创建一个类,他都有UCLASS()。GENERATED_BODY()这样的默认的宏。 UCLASS() 告知虚幻引擎生成类的反射数据。类必须派生自UObject. (告诉引擎我是从远古大帝UObject中,继承而来,我们是一家人,只是我进化了其他功能…...
SpringBoot整合SSE
目录 1.SseController2. SseServiceSseServiceSseServiceImpl 3.SendMessageTask4.将定时任务加入启动类5.参考资料 1.SseController Slf4j RestController RequestMapping("sse") public class SseController {Autowiredprivate SseService sseService;RequestMappi…...
mysql-进阶篇
文章目录 存储引擎MySQL体系结构相关操作 存储引擎特点InnoDBInnoDB 逻辑存储结构 MyISAMMemory三个存储引擎之间的区别存储引擎的选择 索引1. 索引结构B-TreeB-Tree (多路平衡查找树)B-Tree演变过程 BTree与 B-Tree 的区别BTree演变过程 Hash 2.索引分类3.索引语法演示 4.SQL性…...

Js中的构造函数
在JavaScript中,构造函数是一种特殊类型的方法,用于创建并初始化一个新的对象。它通常使用 new 关键字来调用,并且通常以大写字母开头,以与其他非构造函数区分开来。 一个简单的构造函数示例: function Person(name,…...

[小程序]页面事件
一、下拉刷新 1.开启和配置 小程序中开启下拉刷新的方式有两种: ①全局开启下来刷新 在app.json的window节点中,设置enablePullDownRefresh设为ture。 ②局部开启下来刷新 在页面对应的json文件的的window节点中,设置enablePullDownRefresh设…...
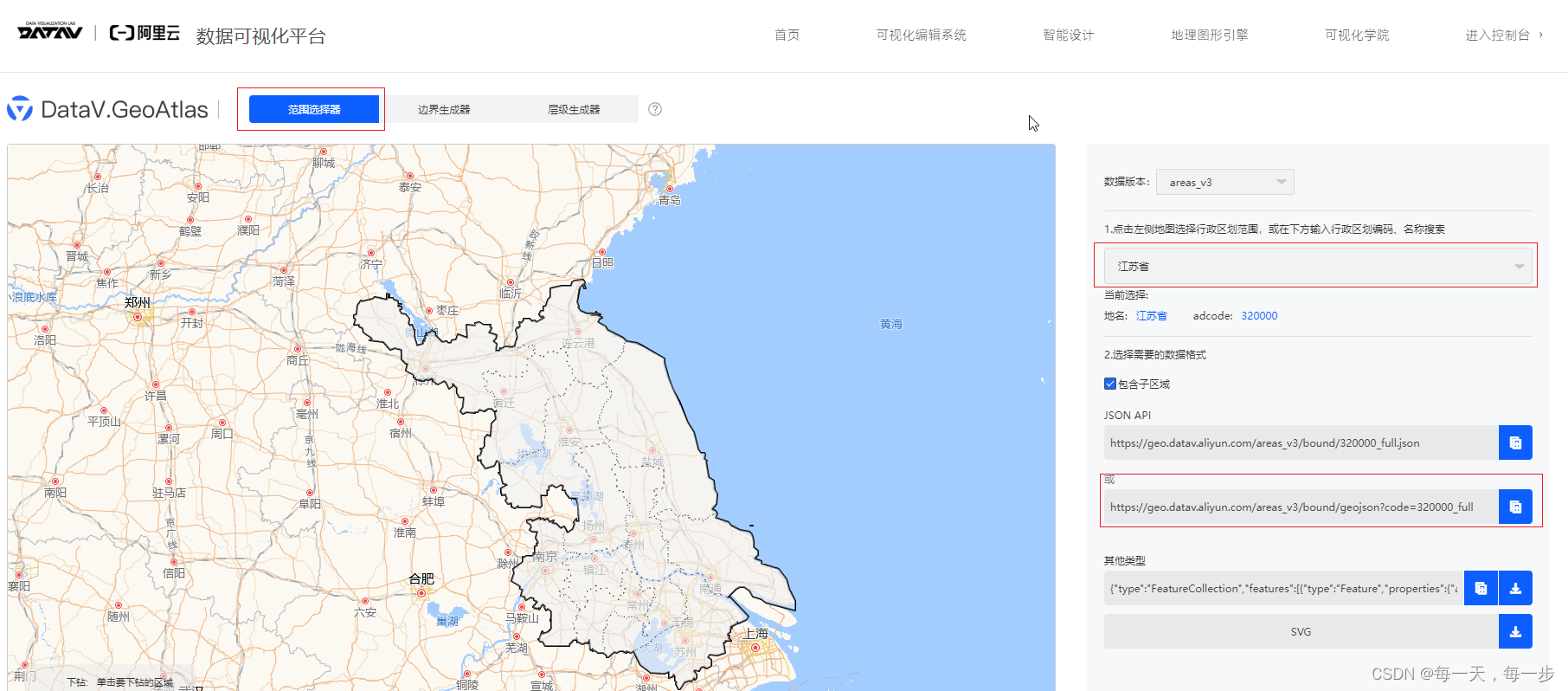
vue echarts地图
下载地图文件: DataV.GeoAtlas地理小工具系列 范围选择器右侧行政区划范围中输入需要选择的省份或地市,选择自己想要的数据格式,这里选择了geojson格式,点右侧的蓝色按钮复制到浏览器地址栏中,打开的geojson文件内容…...

v38.Switch语句
1.Switch语句可以替代if-else语句 2.具体使用 Switch(expression) { case label:...... } ①将x与case后的label 进行比较; ②注意后面有冒号; ③从上往下开始检查case; ④如果…...

如何进行产品的人机交互设计?
产品的人机交互设计是指通过用户界面和用户体验设计来优化产品与用户之间的交互过程,从而提高产品的易用性、可用性和用户满意度。人机交互设计需要考虑用户的需求、行为模式、心理感受以及技术实现,下面我将介绍如何进行产品的人机交互设计。 首先&…...

【ARMv8M Cortex-M33 系列 7.3 -- EXC_RETURN 与 LR 及 PC 的关系详细介绍】
请阅读【嵌入式开发学习必备专栏 之 ARM Cortex-Mx专栏】 文章目录 背景EXC_RETURN 与 LR 及 PCcortex-m33 从异常返回后 各个寄存器出战顺序ARM 栈增长方式 背景 接着上篇文章:【ARMv8M Cortex-M33 系列 7.2 – HardFault 问题定位 1】,后面定位到是在…...

Linux之权限(内容详细,细节满满)
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 数据结构初阶 Linux 欢迎大家点赞,评论,收藏。 一起努力 目录 一.前言 二.权限修改的两种方法 …...

了解云工作负载保护:技术和最佳实践
云工作负载是指云环境中的应用程序或存储元素,无论是公共云、私有云还是混合云。每个云工作负载都使用云的资源,包括计算、网络和存储。 云工作负载可以多种多样,例如运行应用程序、数据库或托管网站。它们可以是静态的或动态的,…...
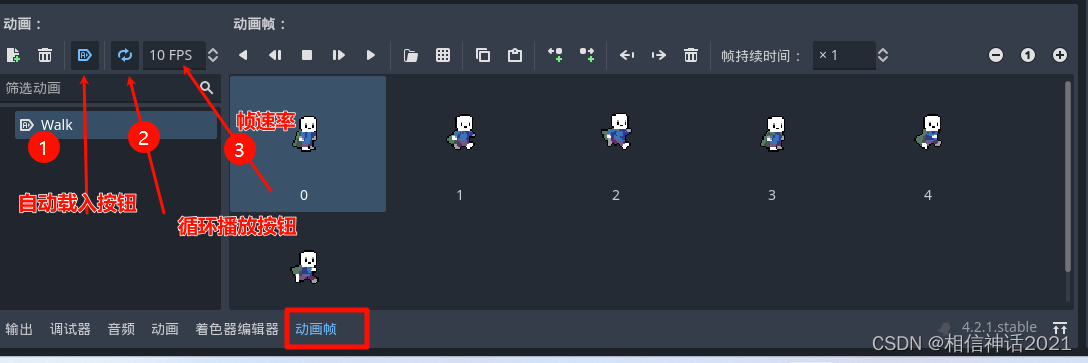
【Godot4自学手册】第三节设置主人公的动画
继续,今天是第三节,我们主要实现主人公的动画效果,共有两种方法实现动画效果 一、通过AnimationPlayer节点实现动画效果 我们首先在player场景下,player节点下添加AnimationPlayer节点,添加方法是,在play…...
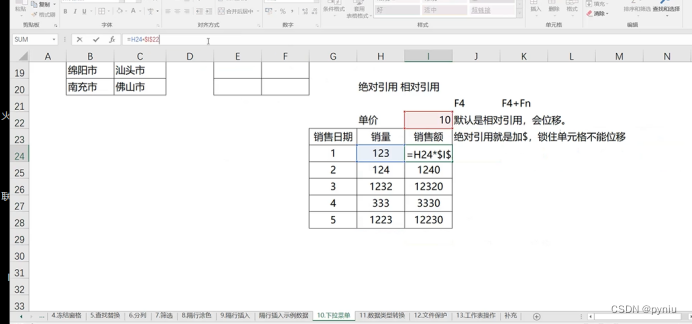
excel学习1
直接ctrl cctrl v会报错位移选择粘贴时用123那个数字粘贴而不是ctrl V 只要结果不要公式 上面复制的为数值这里是复制的公式他们两个不一样 这个方法太麻烦了直接用格式刷,选择一个区域一个单元格,不要选择多个一刷就出来了 第一个计算后向下拖就行了&…...

裁员致谷歌中国籍程序员身亡,技术变革下裁员对程序员的影响有多大
裁员,这是一个令无数人心悸的词汇。在瞬息万变的科技时代,裁员仿佛成了不少公司应对困境的“救命稻草”。然而,在这背后,每一名员工,每一个程序员,他们所承担的代价,又有多少人能够深切地理解&a…...

MybatisPlus的主键ID生成策略和公共字段自动填充的使用及注意事项
主键策略(ID自动生成) 以下是MyBatis-Plus中常见的几种主键生成策略及其对应的枚举值(3.3.0之前的版本): 主键生成策略枚举值数据库自增IdType.AUTO用户输入IdType.INPUT分布式全局唯一IDIdType.ID_WORKER分布式全局…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
