kmp算法
前缀函数
π[i]=maxk=0,⋯,i{k∣s[0,⋯,k−1]==s[i−(k−1),⋯,i]}\pi\left[i\right] = \max\limits_{k = 0,\cdots, i}\left\{k|s\left[0,\cdots,k-1\right] == s\left[i-\left(k-1\right) ,\cdots, i\right]\right\} π[i]=k=0,⋯,imax{k∣s[0,⋯,k−1]==s[i−(k−1),⋯,i]}
简单来说就是最长的相等的真前缀与真后缀的长度
字符串前缀函数求法
我们要求整个字符串每一个位置的前缀函数
最暴力的做法就是枚举,但是这样时间复杂度O(n3)O\left(n^3\right)O(n3)
优化
优化1
计算π[i+1]\pi\left[i+1\right]π[i+1]的时候,不需要从iii枚举到000,可以从π[i]+1\pi\left[i\right] +1π[i]+1枚举到000
也就是说前缀函数至多增加1
证明:
由定义s[0,⋯,π[i]−1]==s[i−(π[i]−1),⋯,i]s\left[0,\cdots,\pi\left[i\right]-1\right] == s\left[i-\left(\pi\left[i\right]-1\right) ,\cdots, i\right]s[0,⋯,π[i]−1]==s[i−(π[i]−1),⋯,i]
并且∀k≥1,s[0,⋯,π[i]−1+k]≠s[i−(π[i]−1)−k,⋯,i]\forall k \ge 1,s\left[0,\cdots,\pi\left[i\right]-1+k\right] \neq s\left[i-\left(\pi\left[i\right]-1\right)-k ,\cdots, i\right]∀k≥1,s[0,⋯,π[i]−1+k]=s[i−(π[i]−1)−k,⋯,i]
如果π[i+1]=π[i]+1+k\pi\left[i+1\right] = \pi\left[i\right] +1 + kπ[i+1]=π[i]+1+k,其中k≥1k\ge 1k≥1
那么意味着s[0,⋯,π[i]+k]==s[i+1−(π[i]+k+1−1),⋯,i+1]s\left[0,\cdots,\pi\left[i\right] + k\right] == s\left[i + 1-\left(\pi\left[i\right] + k +1-1\right) ,\cdots, i+1\right]s[0,⋯,π[i]+k]==s[i+1−(π[i]+k+1−1),⋯,i+1]
于是s[0,⋯,π[i]+k−1]==s[i−(π[i]+k−1),⋯,i]s\left[0,\cdots,\pi\left[i\right] + k - 1\right] == s\left[i-\left(\pi\left[i\right] + k -1\right) ,\cdots, i\right]s[0,⋯,π[i]+k−1]==s[i−(π[i]+k−1),⋯,i]
矛盾
如果s[π[i]]==s[i+1]s\left[\pi\left[i\right]\right] == s\left[i+1\right]s[π[i]]==s[i+1],那么π[i+1]=π[i]+1\pi\left[i+1\right] = \pi\left[i\right] +1π[i+1]=π[i]+1
优化2
如果s[π[i]]≠s[i+1]s\left[\pi\left[i\right]\right] \neq s\left[i+1\right]s[π[i]]=s[i+1]
这时候我们需要找到了一个j<π[i]j < \pi\left[i\right]j<π[i]
使得s[0,⋯,j−1]==s[i−j+1,⋯,i]s\left[0,\cdots,j-1\right] == s\left[i-j+1,\cdots,i\right]s[0,⋯,j−1]==s[i−j+1,⋯,i]
由于s[0,⋯,π[i]−1]==s[i−(π[i]−1),⋯,i]s\left[0,\cdots,\pi\left[i\right]-1\right] == s\left[i-\left(\pi\left[i\right]-1\right) ,\cdots, i\right]s[0,⋯,π[i]−1]==s[i−(π[i]−1),⋯,i]
并且
s[0,⋯,π[π[i]−1]−1]==s[π[i]−1−(π[π[i]−1]−1),⋯,i]s\left[0,\cdots,\pi\left[\pi\left[i\right]-1\right]-1\right] == s\left[\pi\left[i\right]-1-\left(\pi\left[\pi\left[i\right]-1\right]-1\right) ,\cdots, i\right]s[0,⋯,π[π[i]−1]−1]==s[π[i]−1−(π[π[i]−1]−1),⋯,i]
也就是说maxj=π[i]−1\max j = \pi\left[i\right]-1maxj=π[i]−1
简单来说就是前面那一段和后面那一段是一样的,那么我们意味着前后缀也一样,那么最长的前缀就是前缀函数
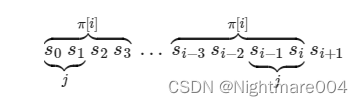
所以我们的过程就是
j(0)=π[i]j^{\left(0\right)} = \pi\left[i\right]j(0)=π[i]
j(i)=π[j(i−1)−1]j^{\left(i\right)}=\pi\left[j^{\left(i-1\right)}-1\right]j(i)=π[j(i−1)−1]
直到s[j(i)]==s[i+1]s\left[j^{\left(i\right)}\right] == s\left[i+1\right]s[j(i)]==s[i+1]或者j(i)=0j^{\left(i\right)} =0j(i)=0
时间复杂度O(n)O\left(n\right)O(n)
kmp
kmp是一个字符串匹配的算法
主要原理就是,如果某一个位置不相等了,就滑到前缀和后缀相等的地方
那么求前缀和后缀相等,我们可以用前缀函数
为了方便,也可以将前缀函数整体向右移一位
因为是iii这个位置不相等,只能找π[i−1]\pi\left[i-1\right]π[i−1]
代码
因为这里用的是数组,所以最好直接存一下字符串长度,不然strlen是O(n)O\left(n\right)O(n)
#include<cstdio>
#include<cstring>const int N = 105;
char pattern[N];//模式串
int len_p;
char text[N];//待匹配串
int len_t;
int nxt[N] = { -1 };//前缀函数void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_p) {if (j == -1 || pattern[i] == pattern[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}int kmp() {int i = 0, j = 0;get_next();while (i < len_t && j < len_p) {if (j == -1 || text[i] == pattern[j]) {++j;++i;}else {j = nxt[j];}}if (j == len_p)return i - j;return -1;
}
洛谷3375
如果匹配了,那么要回到π[lenpattern]\pi\left[len_{pattern}\right]π[lenpattern]
#include<cstdio>
#include<cstring>const int N = 1e6 + 5;
char pattern[N];//模式串
int len_p;
char text[N];//待匹配串
int len_t;
int nxt[N];//前缀函数void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_p) {if (j == -1 || pattern[i] == pattern[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}void kmp() {int i = 0, j = 0;get_next();while (i < len_t) {if (j == -1 || text[i] == pattern[j]) {++i;++j;if (j == len_p) {printf("%d\n", i - j + 1);j = nxt[j];}}else {j = nxt[j];}}
}int main() {scanf("%s%s", text, pattern);len_p = strlen(pattern);len_t = strlen(text);kmp();for (int i = 1; i <= len_p; ++i) {if (i > 1)printf(" ");printf("%d", nxt[i]);}printf("\n");return 0;
}
字符串周期与border
对于字符串sss和0<p≤∣s∣0 < p \le \left|s\right|0<p≤∣s∣,若s[i]==s[i+p]s\left[i\right] == s\left[i + p\right]s[i]==s[i+p]对所有i∈[0,∣s−1∣−p−1]i \in \left[0,\left|s - 1\right| - p - 1\right]i∈[0,∣s−1∣−p−1]成立,则称ppp是sss的周期
对于字符串sss和0≤r<∣s∣0 \le r < \left|s\right|0≤r<∣s∣,若sss长度为rrr的前缀和长度为rrr的后缀相等,则称sss长度为rrr的前缀是sss的border
sss有长度为rrr的border可以推出∣s∣−r\left|s\right| - r∣s∣−r是sss的周期
由前缀函数,可以得到sss所有的的border长度,即π[∣s∣−1],π[π[∣s∣−1]−1],⋯\pi\left[\left|s\right|-1\right],\pi\left[\pi\left[\left|s\right|-1\right]-1\right],\cdotsπ[∣s∣−1],π[π[∣s∣−1]−1],⋯
codeforce432D
统计每一个border出现的次数
首先求出前缀函数
接着建立一个数组cntcntcnt,cnt[i]cnt[i]cnt[i]表示s[0,⋯,i]s\left[0,\cdots,i\right]s[0,⋯,i]出现的次数
初始化cnt[i]=1cnt[i] = 1cnt[i]=1
然后从后往前遍历,cnt[π[i]]+=cnt[i]cnt[\pi\left[i\right]] +=cnt[i]cnt[π[i]]+=cnt[i](建议自己模拟一下
#include<cstdio>
#include<cstring>
#include<stack>
using namespace std;const int N = 1e5 + 5;
char s[N];
int len_s;
int nxt[N];int cnt[N];
void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_s) {if (j == -1 || s[i] == s[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}int main() {scanf("%s", s);len_s = strlen(s);get_next();fill(cnt, cnt + len_s + 1, 1);for (int i = len_s; i > 0; --i) {cnt[nxt[i]] += cnt[i];}stack<int> st;int t = len_s;while (t > 0) {st.push(t);t = nxt[t];}printf("%d\n", st.size());while (!st.empty()) {int temp = st.top();st.pop();printf("%d %d\n", temp, cnt[temp]);}return 0;
}
字符串压缩
给定一个长度为nnn得字符串sss,我们希望找到最短得字符串ttt,使得s=t∗s = t*s=t∗
令k=n−π[n−1]k = n - \pi\left[n-1\right]k=n−π[n−1],如果k∣nk\mid nk∣n,则t=s[0,1,⋯,k]t=s\left[0,1,\cdots, k\right]t=s[0,1,⋯,k]就是答案
否则不存在有效的压缩
证明:
如果k∣nk\mid nk∣n,则字符串可以分成长度为kkk的若干块,
由前缀函数,最后一块等于倒数第二块,进而倒数第二块等于倒数第三块,以此类推
最后所有的块都是相等的
最优性证明:暂时没看懂
poj2406
#include<cstdio>
#include<cstring>const int N = 1e6 + 5;
char s[N];
int len_s;
int nxt[N];void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_s) {if (j == -1 || s[i] == s[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}int main() {while (scanf("%s", s) && s[0] != '.' && s[1] != '\0') {len_s = strlen(s);get_next();int ans = len_s - nxt[len_s];if (ans == 0)printf("1\n");else if (len_s % ans == 0)printf("%d\n", len_s / ans);else printf("1\n");}return 0;
}
相关文章:

kmp算法
前缀函数 π[i]maxk0,⋯,i{k∣s[0,⋯,k−1]s[i−(k−1),⋯,i]}\pi\left[i\right] \max\limits_{k 0,\cdots, i}\left\{k|s\left[0,\cdots,k-1\right] s\left[i-\left(k-1\right) ,\cdots, i\right]\right\} π[i]k0,⋯,imax{k∣s[0,⋯,k−1]s[i−(k−1),⋯,i]} 简单来说…...

【Python】正则表达式简单教程
0x01 正则表达式概念及符号含义 掌握正则表达式,只需要记住不同符号所表示的含义,以及对目标对象模式(或规律)的正确概括。 1、基础内容 字符匹配 在正则表达式中,如果直接给出字符,就是精确匹配。\d 匹…...
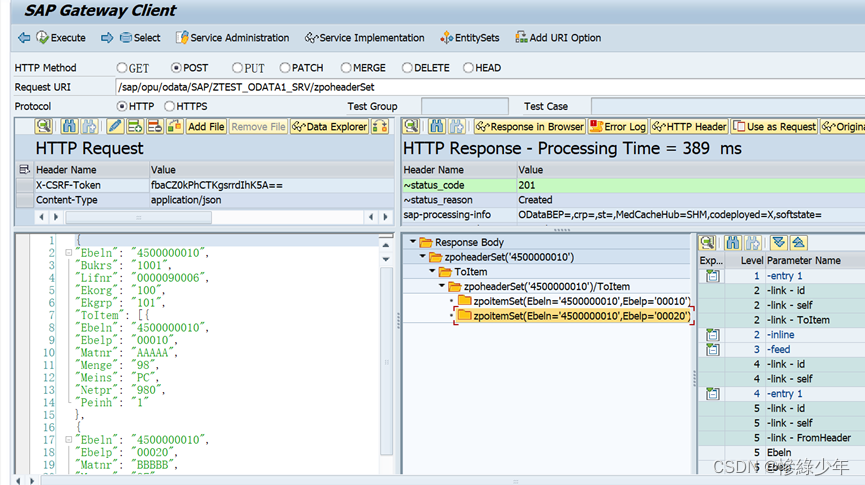
SAP ABAP Odata
GetEntity和GetEntitys GetEntitys 创建Odata Project 导入结构 选择需要的字段 设定Key 勾选字段的creatable、updatable、sortable、nullable、filterable属性值。 再依上述步骤创建ZPOITEM结构和实体集 3. 创建ZPOHEADER和ZPOITEM的Association 两个实体集的关联字段&…...

Android native ASAN 排查内存泄漏
一、概述 android 对native - c/c 的调试和排查是比较难受的一件事。我看周遭做window , linux 甚至ios的调试排查起c的代码都比较方便。习惯了app开发去熟悉native是各种痛苦,最主要是排查问题上。后续有时间打算整理下native 的错误排查使用ÿ…...
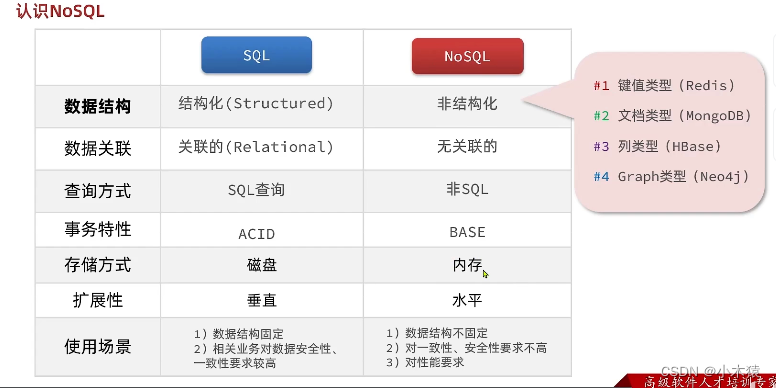
Django项目开发
一.认识NoSQL 1.SQL 关系型数据库 结构化: 定义主键,无符号型数据等关联的:结构化表和表之间的关系通过外键进行关联,节省存储空间SQL查询:语法固定 SELECT id,name,age FROM tb_user WHERE id1 ACID 2.NoSQL 非关系型数据库 Re…...

Debezium系列之:深入理解Debezium Server和Debezium Server实际应用案例详解
Debezium系列之:深入理解Debezium Server和Debezium Server实际应用案例详解 一、认识Debezium Server二、下载Debezium Server三、解压Debezium Server四、查看Debezium Server目录五、Debezium Server配置六、Debezium Server启动输出样式七、源配置八、格式配置九、Transfo…...
IDE2022源码编译tomcat
因为学习需要,我需要源码编译运行tomcat对其源码进行一个简单的追踪分析。由于先前并未接触过java相关的知识,安装阻力巨大。最后请教我的开发朋友才解决了最后的问题。将其整理出来,让大家能够快速完成相关的部署。本文仅解决tomcat-8.5.46版…...

214 情人节来袭,电视剧 《点燃我温暖你》李峋同款 Python爱心表白代码,赶紧拿去用吧
大家好,我是徐公,六年大厂程序员经验,今天为大家带来的是动态心形代码,电视剧 《点燃我温暖你》同款的,大家赶紧看看,拿去向你心仪的对象表白吧,下面说一下灵感来源。 灵感来源 今天ÿ…...

数据库范式
基本概念 函数依赖 x→yx\rightarrow yx→y,当确定xxx的时候,yyy也可以确定 例: 学号→\rightarrow→姓名,当知道了学号,就知道了学生姓名 学号,课程号→\rightarrow→成绩,当知道了学号和课程号ÿ…...
CUDA中的底层驱动API
文章目录CUDA底层驱动API1. Context2. Module3. Kernel Execution4. Interoperability between Runtime and Driver APIs5. Driver Entry Point Access5.1. Introduction5.2. Driver Function Typedefs5.3. Driver Function Retrieval5.3.1. Using the driver API5.3.2. Using …...

【博客616】prometheus staleness对PromQL查询的影响
prometheus staleness对PromQL查询的影响 1、prometheus staleness 官方文档的解释: 概括: 运行查询时,将独立于实际的当前时间序列数据选择采样数据的时间戳。这主要是为了支持聚合(sum、avg 等)等情况,…...

多传感器融合定位十三-基于图优化的建图方法其二
多传感器融合定位十二-基于图优化的建图方法其二3.4 预积分方差计算3.4.1 核心思路3.4.2 连续时间下的微分方程3.4.3 离散时间下的传递方程3.5 预积分更新4. 典型方案介绍4.1 LIO-SAM介绍5. 融合编码器的优化方案5.1 整体思路介绍5.2 预积分模型设计Reference: 深蓝学院-多传感…...
linux 服务器线上问题故障排查
一 线上故障排查概述 1.1 概述 线上故障排查一般从cpu,磁盘,内存,网络这4个方面入手; 二 磁盘的排查 2.1 磁盘排查 1.使用 df -hl 命令来查看磁盘使用情况 2.从读写性能排查:iostat -d -k -x命令来进行分析 最后一列%util可以看到每块磁盘写入的程度,而rrqpm/s以及…...

Sandman:一款基于NTP协议的红队后门研究工具
关于Sandman Sandman是一款基于NTP的强大后门工具,该工具可以帮助广大研究人员在一个安全增强型网络系统中执行红队任务。 Sandman可以充当Stager使用,该工具利用了NTP(一个用于计算机时间/日期同步协议)从预定义的服务器获取并…...
【SSL/TLS】准备工作:HTTPS服务器部署:Nginx部署
HTTPS服务器部署:Nginx部署1. 准备工作2. Nginx服务器YUM部署2.1 直接安装2.2 验证3. Nginx服务器源码部署3.1 下载源码包3.2 部署过程4. Nginx基本操作4.1 nginx常用命令行4.2 nginx重要目录1. 准备工作 1. Linux版本 [rootlocalhost ~]# cat /proc/version Li…...
微搭低代码从入门到精通11-数据模型
学习微搭低代码,先学习基本操作,然后学习组件的基本使用。解决了前端的问题,我们就需要深入学习后端的功能。后端一般包括两部分,第一部分是常规的数据库的操作,包括增删改查。第二部分是业务逻辑的编写,在…...

【算法基础】前缀和与差分
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法💪种一棵树最好是十年前其次是现在1.什么是前缀和前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身&#x…...
LTD212次升级 | 官网社区支持PC端展示 • 官网新增证件查询应用,支持条形码扫码查询
1、新增证件查询应用,支持条形码扫码查询; 2、新增用户社区PC端功能; 01证件查询应用 1、新增证件查询应用功能 支持证件信息录入、打印功能,支持条形码扫码识别。 后台管理操作路径:官微中心 - 应用 - 证件查询 …...
【安全】nginx反向代理+负载均衡上传webshell
目录 一、负载均衡反向代理下上传webshell Ⅰ、环境搭建 ①下载蚁剑,于github获取官方版: ②下载docker&docker-compose ③结合前面启动环境 ④验证 负载均衡下webshell上传 一、负载均衡反向代理下上传webshell 什么是反向代理? 通常的代…...
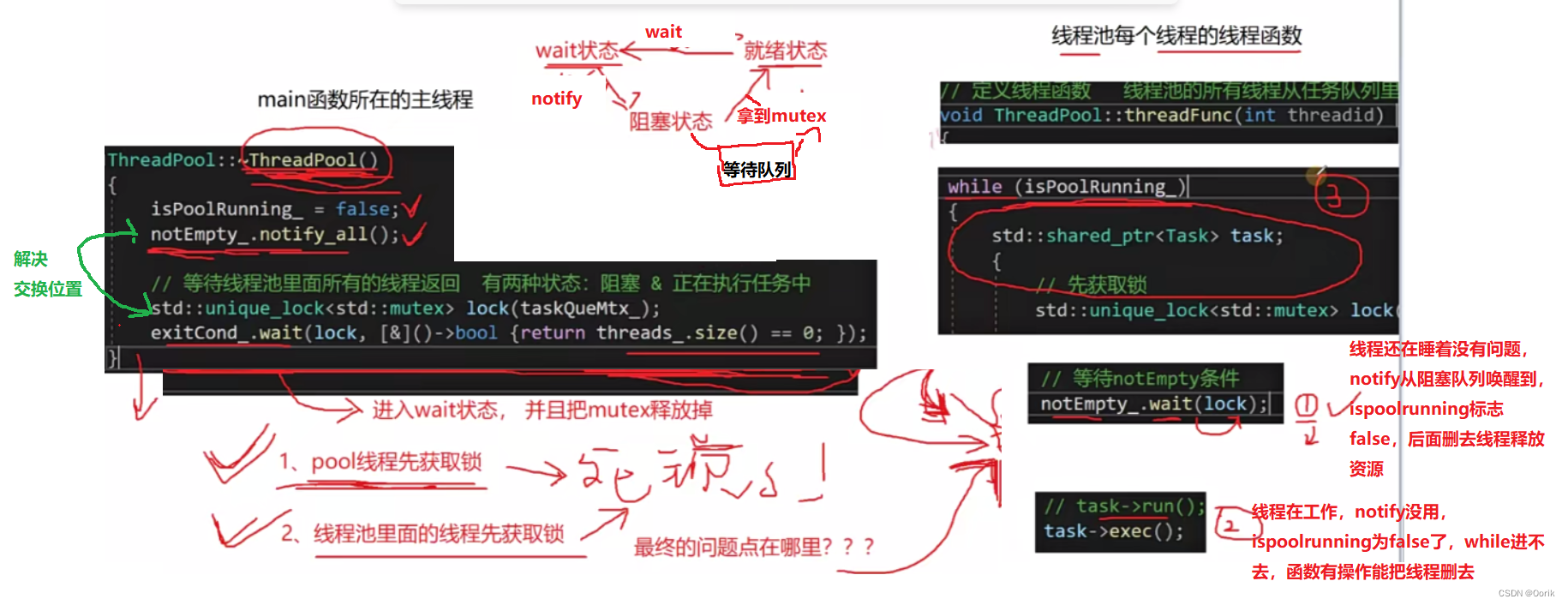
线程池框架
这是之前有做的一个可以接受用户传入任意类型的任务函数和任意参数,并且能拿到任务对应返回值的一个线程池框架,可以链接成动态库,用在相关项目里面。一共实现了两版,都是支持fixed和cached模式的,半同步半异步的&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
