多传感器融合定位十三-基于图优化的建图方法其二
多传感器融合定位十二-基于图优化的建图方法其二
- 3.4 预积分方差计算
- 3.4.1 核心思路
- 3.4.2 连续时间下的微分方程
- 3.4.3 离散时间下的传递方程
- 3.5 预积分更新
- 4. 典型方案介绍
- 4.1 LIO-SAM介绍
- 5. 融合编码器的优化方案
- 5.1 整体思路介绍
- 5.2 预积分模型设计
Reference:
- 深蓝学院-多传感器融合
- 多传感器融合定位理论基础
文章跳转:
- 多传感器融合定位一-3D激光里程计其一:ICP
- 多传感器融合定位二-3D激光里程计其二:NDT
- 多传感器融合定位三-3D激光里程计其三:点云畸变补偿
- 多传感器融合定位四-3D激光里程计其四:点云线面特征提取
- 多传感器融合定位五-点云地图构建及定位
- 多传感器融合定位六-惯性导航原理及误差分析
- 多传感器融合定位七-惯性导航解算及误差分析其一
- 多传感器融合定位八-惯性导航解算及误差分析其二
- 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
- 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
- 多传感器融合定位十一-基于滤波的融合方法Ⅱ
- 多传感器融合定位十二-基于图优化的建图方法其一
- 多传感器融合定位十三-基于图优化的建图方法其二
- 多传感器融合定位十四-基于图优化的定位方法
- 多传感器融合定位十五-多传感器时空标定(综述)
3.4 预积分方差计算
3.4.1 核心思路
在融合时,需要给不同信息设置权重,而权重由方差得来,因此对于IMU积分,也要计算其方差。方差的计算形式与第四章相同,即:
Pi,k+1=FkPi,kFk⊤+BkQBk⊤\boldsymbol{P}_{i, k+1}=\mathbf{F}_k \boldsymbol{P}_{i, k} \mathbf{F}_k^{\top}+\mathbf{B}_k \boldsymbol{Q} \mathbf{B}_k^{\top} Pi,k+1=FkPi,kFk⊤+BkQBk⊤但需注意的是,此处 Fk\boldsymbol{F}_kFk 和 Gk\boldsymbol{G}_kGk 是离散时间下的状态传递方程中的矩阵,而我们一般是在连续时间下推导微分方程,再用它计算离散时间下的传递方程。
3.4.2 连续时间下的微分方程
连续时间下的微分方程一般写为如下形式:
x˙=Ftx+Btwx=[δαtbkδθtbkδβtbkδbatδbwt]w=[nanwnbanbw]\begin{gathered} \dot{\boldsymbol{x}}=\boldsymbol{F}_t \boldsymbol{x}+\boldsymbol{B}_t \boldsymbol{w} \\ \boldsymbol{x}=\left[\begin{array}{l} \delta \boldsymbol{\alpha}_t^{b_k} \\ \delta \boldsymbol{\theta}_t^{b_k} \\ \delta \boldsymbol{\beta}_t^{b_k} \\ \delta \boldsymbol{b}_{\boldsymbol{a}_t} \\ \delta \boldsymbol{b}_{w_t} \end{array}\right] \\ \boldsymbol{w}=\left[\begin{array}{l} \boldsymbol{n}_a \\ \boldsymbol{n}_w \\ \boldsymbol{n}_{b_a} \\ \boldsymbol{n}_{b_w} \end{array}\right] \end{gathered} x˙=Ftx+Btwx=δαtbkδθtbkδβtbkδbatδbwtw=nanwnbanbw以上变量排列顺序是为了与lio/vio等常见系统顺序保持一致。
推导方法已经在第6讲介绍,此处直接给出结果:
δθ˙tbk\delta \dot{\boldsymbol{\theta}}_t^{b_k}δθ˙tbk 的微分方程:
δθ˙tbk=−[ωt−bωt]×δθtbk+nω−δbωt\delta \dot{\boldsymbol{\theta}}_t^{b_k}=-\left[\boldsymbol{\omega}_t-\boldsymbol{b}_{\omega_t}\right]_{\times} \delta \boldsymbol{\theta}_t^{b_k}+\boldsymbol{n}_\omega-\delta \boldsymbol{b}_{\omega_t} δθ˙tbk=−[ωt−bωt]×δθtbk+nω−δbωtδβ˙tbk\delta \dot{\boldsymbol{\beta}}_t^{b_k}δβ˙tbk 的微分方程:
δβ˙tbk=−Rt[at−bat]×δθtbk+Rt(na−δbat)\delta \dot{\boldsymbol{\beta}}_t^{b_k}=-\boldsymbol{R}_t\left[\boldsymbol{a}_t-\boldsymbol{b}_{a_t}\right]_{\times} \delta \boldsymbol{\theta}_t^{b_k}+\boldsymbol{R}_t\left(\boldsymbol{n}_a-\delta \boldsymbol{b}_{a_t}\right) δβ˙tbk=−Rt[at−bat]×δθtbk+Rt(na−δbat)δα˙tbk\delta \dot{\boldsymbol{\alpha}}_t^{b_k}δα˙tbk 的微分方程:
δα˙tbk=δβtbk\delta \dot{\boldsymbol{\alpha}}_t^{b_k}=\delta \boldsymbol{\beta}_t^{b_k} δα˙tbk=δβtbk
3.4.3 离散时间下的传递方程
得到连续时间微分方程以后,就可以计算离散时间的递推方程了,表示为:
xk+1=Fkxk+Bkwk\boldsymbol{x}_{k+1}=\boldsymbol{F}_k \boldsymbol{x}_k+\boldsymbol{B}_k \boldsymbol{w}_k xk+1=Fkxk+Bkwk其中:
xk+1=[δαk+1δθk+1δβk+1δbak+1δbωk+1]xk=[δαkδθkδβkδbakδbωk]wk=[naknwknak+1nwk+1nbanbw]\boldsymbol{x}_{k+1}=\left[\begin{array}{l} \delta \boldsymbol{\alpha}_{k+1} \\ \delta \boldsymbol{\theta}_{k+1} \\ \delta \boldsymbol{\beta}_{k+1} \\ \delta \boldsymbol{b}_{a_{k+1}} \\ \delta \boldsymbol{b}_{\omega_{k+1}} \end{array}\right] \quad \boldsymbol{x}_k=\left[\begin{array}{c} \delta \boldsymbol{\alpha}_k \\ \delta \boldsymbol{\theta}_k \\ \delta \boldsymbol{\beta}_k \\ \delta \boldsymbol{b}_{a_k} \\ \delta \boldsymbol{b}_{\omega_k} \end{array}\right] \quad \boldsymbol{w}_k=\left[\begin{array}{c} \boldsymbol{n}_{a_k} \\ \boldsymbol{n}_{w_k} \\ \boldsymbol{n}_{a_{k+1}} \\ \boldsymbol{n}_{w_{k+1}} \\ \boldsymbol{n}_{b_a} \\ \boldsymbol{n}_{b_w} \end{array}\right] xk+1=δαk+1δθk+1δβk+1δbak+1δbωk+1xk=δαkδθkδβkδbakδbωkwk=naknwknak+1nwk+1nbanbw
-
δθk+1\delta \boldsymbol{\theta}_{k+1}δθk+1 的求解
由于连续时间下有
δθ˙=−[ωt−bωt]×δθ+nω−δbωt\delta \dot{\boldsymbol{\theta}}=-\left[\boldsymbol{\omega}_t-\boldsymbol{b}_{\omega_t}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{n}_\omega-\delta \boldsymbol{b}_{\omega_t} δθ˙=−[ωt−bωt]×δθ+nω−δbωt则离散时间下应该有
因此有
δθ˙k=−[ωk+ωk+12−bωt]×δθk+nωk+nωk+12−δbωkδθk+1=[I−[ωk+ωk+12−bωk]×δt]δθk+δtnωk+nωk+12−δtδbωk\delta \dot{\boldsymbol{\theta}}_k=-\left[\frac{\boldsymbol{\omega}_k+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_t}\right]_{\times} \delta \boldsymbol{\theta}_k+\frac{\boldsymbol{n}_{\omega_k}+\boldsymbol{n}_{\omega_{k+1}}}{2}-\delta \boldsymbol{b}_{\omega_k}\\ \delta \boldsymbol{\theta}_{k+1}=\left[\boldsymbol{I}-\left[\frac{\boldsymbol{\omega}_k+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_k}\right]_{\times} \delta t\right] \delta \boldsymbol{\theta}_k+\delta t \frac{\boldsymbol{n}_{\omega_k}+\boldsymbol{n}_{\omega_{k+1}}}{2}-\delta t \delta \boldsymbol{b}_{\omega_k} δθ˙k=−[2ωk+ωk+1−bωt]×δθk+2nωk+nωk+1−δbωkδθk+1=[I−[2ωk+ωk+1−bωk]×δt]δθk+δt2nωk+nωk+1−δtδbωk令 ω‾=ωk+ωk+12−bωk\overline{\boldsymbol{\omega}}=\frac{\omega_k+\omega_{k+1}}{2}-\boldsymbol{b}_{\omega_k}ω=2ωk+ωk+1−bωk ,则上式可以重新写为
δθk+1=[I−[ω‾]×δt]δθk+δt2nωk+δt2nωk+1−δtδbωk\delta \boldsymbol{\theta}_{k+1}=\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_k+\frac{\delta t}{2} \boldsymbol{n}_{\omega_k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_k} δθk+1=[I−[ω]×δt]δθk+2δtnωk+2δtnωk+1−δtδbωk -
δβk+1\delta \boldsymbol{\beta}_{k+1}δβk+1 的求解
由于连续时间下有
δβ˙=−Rt[at−bat]×δθ+Rt(na−δbat)\delta \dot{\boldsymbol{\beta}}=-\boldsymbol{R}_t\left[\boldsymbol{a}_t-\boldsymbol{b}_{a_t}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{R}_t\left(\boldsymbol{n}_a-\delta \boldsymbol{b}_{a_t}\right) δβ˙=−Rt[at−bat]×δθ+Rt(na−δbat)
则离散时间下应该有
δβ˙k=−12Rk[ak−bak]×δθk−12Rk+1[ak+1−bak]×δθk+1+12Rknak+12Rk+1nak+1−12(Rk+Rk+1)δbak\begin{aligned} \delta \dot{\boldsymbol{\beta}}_k= & -\frac{1}{2} \boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times} \delta \boldsymbol{\theta}_k \\ & -\frac{1}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \delta \boldsymbol{\theta}_{k+1} \\ & +\frac{1}{2} \boldsymbol{R}_k \boldsymbol{n}_{a_k} \\ & +\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ & -\frac{1}{2}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_k} \end{aligned} δβ˙k=−21Rk[ak−bak]×δθk−21Rk+1[ak+1−bak]×δθk+1+21Rknak+21Rk+1nak+1−21(Rk+Rk+1)δbak把前面求得的 δθk+1\delta \boldsymbol{\theta}_{k+1}δθk+1 的表达式代入上式,可得
δβ˙k=−12Rk[ak−bak]×δθk−12Rk+1[ak+1−bak]×{[I−[ω‾]×δt]δθk+δt2nωk+δt2nωk+1−δtδbωk}+12Rknak+12Rk+1nak+1−12(Rk+Rk+1)δbak\begin{aligned} \delta \dot{\boldsymbol{\beta}}_k= & -\frac{1}{2} \boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times} \delta \boldsymbol{\theta}_k \\ & -\frac{1}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times}\left\{\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_k+\frac{\delta t}{2} \boldsymbol{n}_{\omega_k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_k}\right\} \\ & +\frac{1}{2} \boldsymbol{R}_k \boldsymbol{n}_{a_k} \\ & +\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ & -\frac{1}{2}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_k} \end{aligned} δβ˙k=−21Rk[ak−bak]×δθk−21Rk+1[ak+1−bak]×{[I−[ω]×δt]δθk+2δtnωk+2δtnωk+1−δtδbωk}+21Rknak+21Rk+1nak+1−21(Rk+Rk+1)δbak经过一系列合并同类项以后,最终的合并结果为
δβ˙k=−12[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]δθk−δt4Rk+1[ak+1−bak]×nωk−δt4Rk+1[ak+1−bak]×nωk+1+δt2Rk+1[ak+1−bak]×δbωk+12Rknak+12Rk+1nak+1−12(Rk+Rk+1)δbak\begin{aligned} \delta \dot{\boldsymbol{\beta}}_k= & -\frac{1}{2}\left[\boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_k \\ & -\frac{\delta t}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \boldsymbol{n}_{\omega_k} \\ & -\frac{\delta t}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ & +\frac{\delta t}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \delta \boldsymbol{b}_{\omega_k} \\ & +\frac{1}{2} \boldsymbol{R}_k \boldsymbol{n}_{a_k} \\ & +\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ & -\frac{1}{2}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_k} \end{aligned} δβ˙k=−21[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]δθk−4δtRk+1[ak+1−bak]×nωk−4δtRk+1[ak+1−bak]×nωk+1+2δtRk+1[ak+1−bak]×δbωk+21Rknak+21Rk+1nak+1−21(Rk+Rk+1)δbak由导数形式可以得到递推形式如下
δβk+1=δβk−δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]δθk−δt24Rk+1[ak+1−bak]×nωk−δt24Rk+1[ak+1−bak]×nωk+1+δt22Rk+1[ak+1−bak]×δbωk+δt2Rknak+δt2Rk+1nak+1−δt2(Rk+Rk+1)δbak\begin{aligned} \delta \boldsymbol{\beta}_{k+1}= & \delta \boldsymbol{\beta}_k \\ & -\frac{\delta t}{2}\left[\boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_k \\ & -\frac{\delta t^2}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \boldsymbol{n}_{\omega_k} \\ & -\frac{\delta t^2}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ & +\frac{\delta t^2}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \delta \boldsymbol{b}_{\omega_k} \\ & +\frac{\delta t}{2} \boldsymbol{R}_k \boldsymbol{n}_{a_k} \\ & +\frac{\delta t}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ & -\frac{\delta t}{2}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_k} \end{aligned} δβk+1=δβk−2δt[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]δθk−4δt2Rk+1[ak+1−bak]×nωk−4δt2Rk+1[ak+1−bak]×nωk+1+2δt2Rk+1[ak+1−bak]×δbωk+2δtRknak+2δtRk+1nak+1−2δt(Rk+Rk+1)δbak -
δαk+1\delta \boldsymbol{\alpha}_{k+1}δαk+1 的求解
由于连续时间下有 δα˙t=δβt\delta \dot{\boldsymbol{\alpha}}_t=\delta \boldsymbol{\beta}_tδα˙t=δβt ,则离散时间下应该有
δα˙k=12δβk+12δβk+1=δβk−δt4[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]δθk−δt28Rk+1[ak+1−bak]×nωk−δt28Rk+1[ak+1−bak]×nωk+1+δt24Rk+1[ak+1−bak]×δbωk+δt4Rknak+δt4Rk+1nak+1−δt4(Rk+Rk+1)δbak\begin{aligned} \delta \dot{\boldsymbol{\alpha}}_k= & \frac{1}{2} \delta \boldsymbol{\beta}_k+\frac{1}{2} \delta \boldsymbol{\beta}_{k+1} \\ = & \delta \boldsymbol{\beta}_k \\ & -\frac{\delta t}{4}\left[\boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_k \\ & -\frac{\delta t^2}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{\boldsymbol{a}_k}\right]_{\times} \boldsymbol{n}_{\omega_k} \\ & -\frac{\delta t^2}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{\boldsymbol{a}_k}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ & +\frac{\delta t^2}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{\boldsymbol{a}_k}\right] \times \delta \boldsymbol{b}_{\omega_k} \\ & +\frac{\delta t}{4} \boldsymbol{R}_k \boldsymbol{n}_{a_k} \\ & +\frac{\delta t}{4} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ & -\frac{\delta t}{4}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_k} \end{aligned} δα˙k==21δβk+21δβk+1δβk−4δt[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]δθk−8δt2Rk+1[ak+1−bak]×nωk−8δt2Rk+1[ak+1−bak]×nωk+1+4δt2Rk+1[ak+1−bak]×δbωk+4δtRknak+4δtRk+1nak+1−4δt(Rk+Rk+1)δbak由导数形式可以写出递推形式
δαk+1=δαk+δtδβk−δt24[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ωˉ]×δt)]δθk−δt38Rk+1[ak+1−bak]×nωk−δt38Rk+1[ak+1−bak]×nωk+1+δt34Rk+1[ak+1−bak]×δbωk+δt24Rknak+δt24Rk+1nak+1−δt24(Rk+Rk+1)δbak\begin{aligned} \delta \boldsymbol{\alpha}_{k+1}= & \delta \boldsymbol{\alpha}_k \\ & +\delta t \delta \boldsymbol{\beta}_k \\ & -\frac{\delta t^2}{4}\left[\boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times}\left(\boldsymbol{I}-[\bar{\omega}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_k \\ & -\frac{\delta t^3}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \boldsymbol{n}_{\omega_k} \\ & -\frac{\delta t^3}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ & +\frac{\delta t^3}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \delta \boldsymbol{b}_{\omega_k} \\ & +\frac{\delta t^2}{4} \boldsymbol{R}_k \boldsymbol{n}_{a_k} \\ & +\frac{\delta t^2}{4} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ & -\frac{\delta t^2}{4}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_k} \end{aligned} δαk+1=δαk+δtδβk−4δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ωˉ]×δt)]δθk−8δt3Rk+1[ak+1−bak]×nωk−8δt3Rk+1[ak+1−bak]×nωk+1+4δt3Rk+1[ak+1−bak]×δbωk+4δt2Rknak+4δt2Rk+1nak+1−4δt2(Rk+Rk+1)δbak由以上的推导结果,便可以写出 xk+1=Fkxk+Bkwk\boldsymbol{x}_{k+1}=\boldsymbol{F}_k \boldsymbol{x}_k+\boldsymbol{B}_k \boldsymbol{w}_kxk+1=Fkxk+Bkwk 中的矩阵
Fk=[If12Iδt−14(Rk+Rk+1)δt2f150I−[ω‾]×δt00−Iδt0f32I−12(Rk+Rk+1)δtf35000I00000I]Bk=[14Rkδt2g1214Rk+1δt2g1400012Iδt012Iδt0012Rkδtg3212Rk+1δtg34000000Iδt000000Iδt]\begin{aligned} & \mathbf{F}_k= {\left[\begin{array}{cccccc} \mathbf{I} & \mathbf{f}_{12} & \mathbf{I} \delta t & -\frac{1}{4}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta t^2 & \mathbf{f}_{15} \\ \mathbf{0} & \mathbf{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t & \mathbf{0} & \mathbf{0} & -\mathbf{I} \delta t \\ \mathbf{0} & \mathbf{f}_{32} & \mathbf{I} & -\frac{1}{2}\left(\boldsymbol{R}_k+\boldsymbol{R}_{k+1}\right) \delta t & \mathbf{f}_{35} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \end{array}\right] } \\ & \mathbf{B}_k=\left[\begin{array}{cccccc} \frac{1}{4} \boldsymbol{R}_k \delta t^2 & \mathbf{g}_{12} & \frac{1}{4} \boldsymbol{R}_{k+1} \delta t^2 & \mathbf{g}_{14} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \mathbf{0} \\ \frac{1}{2} \boldsymbol{R}_k \delta t & \mathbf{g}_{32} & \frac{1}{2} \boldsymbol{R}_{k+1} \delta t & \mathbf{g}_{34} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t \end{array}\right] \end{aligned} Fk=I0000f12I−[ω]×δtf3200Iδt0I00−41(Rk+Rk+1)δt20−21(Rk+Rk+1)δtI0f15−Iδtf350IBk=41Rkδt2021Rkδt00g1221Iδtg320041Rk+1δt2021Rk+1δt00g1421Iδtg3400000Iδt00000Iδt上面的矩阵中,有
f12=−δt24[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]f15=δt34Rk+1[ak+1−bak]×δbωkf32=−δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]f35=δt22Rk+1[ak+1−bak]×g12=−δt38Rk+1[ak+1−bak]×g14=−δt38Rk+1[ak+1−bak]×g32=−δt24Rk+1[ak+1−bak]×g34=−δt24Rk+1[ak+1−bak]×\begin{aligned} & \boldsymbol{f}_{12}=-\frac{\delta t^2}{4}\left[\boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ & \boldsymbol{f}_{15}=\frac{\delta t^3}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \delta \boldsymbol{b}_{\omega_k} \\ & \boldsymbol{f}_{32}=-\frac{\delta t}{2}\left[\boldsymbol{R}_k\left[\boldsymbol{a}_k-\boldsymbol{b}_{a_k}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ & \boldsymbol{f}_{35}=\frac{\delta t^2}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \\ & \boldsymbol{g}_{12}=-\frac{\delta t^3}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \\ & \boldsymbol{g}_{14}=-\frac{\delta t^3}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \\ & \boldsymbol{g}_{32}=-\frac{\delta t^2}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \\ & \boldsymbol{g}_{34}=-\frac{\delta t^2}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_k}\right]_{\times} \end{aligned} f12=−4δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]f15=4δt3Rk+1[ak+1−bak]×δbωkf32=−2δt[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]f35=2δt2Rk+1[ak+1−bak]×g12=−8δt3Rk+1[ak+1−bak]×g14=−8δt3Rk+1[ak+1−bak]×g32=−4δt2Rk+1[ak+1−bak]×g34=−4δt2Rk+1[ak+1−bak]×
3.5 预积分更新
回到bias变化时,预积分结果怎样重新计算的 问题,再次给出它的泰勒展开形式:
αbibj=α‾bibj+Jbiaαδbia+Jbigαδbigβbibj=β‾bibj+Jbiaβδbia+Jbigβδbigqbibj=q‾bibj⊗[112Jbiqqδbig]\begin{gathered} \boldsymbol{\alpha}_{b_i b_j}=\overline{\boldsymbol{\alpha}}_{b_i b_j}+\mathbf{J}_{b_i^a}^\alpha \delta \mathbf{b}_i^a+\mathbf{J}_{b_i^g}^\alpha \delta \mathbf{b}_i^g \\ \boldsymbol{\beta}_{b_i b_j}=\overline{\boldsymbol{\beta}}_{b_i b_j}+\mathbf{J}_{b_i^a}^\beta \delta \mathbf{b}_i^a+\mathbf{J}_{b_i^g}^\beta \delta \mathbf{b}_i^g \\ \mathbf{q}_{b_i b_j}=\overline{\mathbf{q}}_{b_i b_j} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \mathbf{J}_{b_i^q}^q \delta \mathbf{b}_i^g \end{array}\right] \end{gathered} αbibj=αbibj+Jbiaαδbia+Jbigαδbigβbibj=βbibj+Jbiaβδbia+Jbigβδbigqbibj=qbibj⊗[121Jbiqqδbig]这里,雅可比没有明确的闭式解,但是在推导 方差的更新时,我们得到了
xk+1=Fkxk+Bkwk\boldsymbol{x}_{k+1}=\boldsymbol{F}_k \boldsymbol{x}_k+\boldsymbol{B}_k \boldsymbol{w}_k xk+1=Fkxk+Bkwk通过该递推形式,可以知道
Jk+1=FkJk\mathbf{J}_{k+1}=\mathbf{F}_k \mathbf{J}_k Jk+1=FkJk即预积分结果的雅可比,可以通过这种迭代方式计算。
Jj\boldsymbol{J}_jJj 中关于 bias 的项,就是预积分泰勒展开时,各 bias 对应的雅可比。
4. 典型方案介绍
4.1 LIO-SAM介绍
论文名称:LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping
代码地址:https://github.com/TixiaoShan/LIO-SAM

最大特点:分两步完成,先通过点云特征计算出相对位姿,再利用相对位姿、IMU预积分和GPS做融合。
相比于直接一步做紧耦合,大大提高了效率,而且实测性能也很优异。
5. 融合编码器的优化方案
5.1 整体思路介绍
理论上,只要是在载体系下测量,且频率比关键帧的提取频率高,就都可以做预积分。
编码器与IMU基于预积分的融合有多种方法,此处选相对简单的一种:
把它们当做一个整体的传感器来用,IMU提供角速度,编码器提供位移增量,且不考虑编码器的误差。
此时对预积分模型,输入为
角速度: ωk=[ωxkωykωzk]\omega_k=\left[\begin{array}{l}\omega_{x k} \\ \omega_{y k} \\ \omega_{z k}\end{array}\right] \quadωk=ωxkωykωzk 位移增量: ϕk=[ϕxk00]\phi_k=\left[\begin{array}{c}\phi_{x k} \\ 0 \\ 0\end{array}\right]ϕk=ϕxk00
输出中包含位置、姿态,但不包含速度。
5.2 预积分模型设计
连续时间下,从 iii 时刻到 jjj 时刻 IMU的积分结果为
pwbj=pwbi+∫t∈[i,j]qwbtϕbtδtqwbj=∫t∈[i,j]qwbt⊗[012ωbt]δt\begin{aligned} \mathbf{p}_{w b_j} & =\mathbf{p}_{w b_i}+\int_{t \in[i, j]} \mathbf{q}_{w b_t} \boldsymbol{\phi}^{b_t} \delta t \\ \mathbf{q}_{w b_j} & =\int_{t \in[i, j]} \mathbf{q}_{w b_t} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_t} \end{array}\right] \delta t \end{aligned} pwbjqwbj=pwbi+∫t∈[i,j]qwbtϕbtδt=∫t∈[i,j]qwbt⊗[021ωbt]δt把 qwbt=qwbi⊗qbibt\mathbf{q}_{w b_t}=\mathbf{q}_{w b_i} \otimes \mathbf{q}_{b_i b_t}qwbt=qwbi⊗qbibt 代入上式可得
pwbj=pwbi+qwbi∫t∈[i,j](qbibtϕbt)δtqwbj=qwbi[∫t∈[i,j]qbibt⊗[012ωbt]δt\mathbf{p}_{w b_j}=\mathbf{p}_{w b_i}+\mathbf{q}_{w b_i} \int_{t \in[i, j]}\left(\mathbf{q}_{b_i b_t} \boldsymbol{\phi}^{b_t}\right) \delta t \\ \mathbf{q}_{w b_j}=\mathbf{q}_{w b_i}\left[\int_{t \in[i, j]} \mathbf{q}_{b_i b_t} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_t} \end{array}\right] \delta t\right. pwbj=pwbi+qwbi∫t∈[i,j](qbibtϕbt)δtqwbj=qwbi[∫t∈[i,j]qbibt⊗[021ωbt]δt为了整理公式,把积分相关的项用下面的式子代替
αbibj=∫t∈[i,j](qbibtϕbt)δtqbibj=∫t∈[i,j]qbibt⊗[012ωbt]δt\begin{aligned} & \boldsymbol{\alpha}_{b_i b_j}=\int_{t \in[i, j]}\left(\mathbf{q}_{b_i b_t} \boldsymbol{\phi}^{b_t}\right) \delta t \\ & \mathbf{q}_{b_i b_j}=\int_{t \in[i, j]} \mathbf{q}_{b_i b_t} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_t} \end{array}\right] \delta t \end{aligned} αbibj=∫t∈[i,j](qbibtϕbt)δtqbibj=∫t∈[i,j]qbibt⊗[021ωbt]δt使用中值积分方法,把连续方法改成离散形式如下
ωb=12[(ωbk−bkg)+(ωbk+1−bkg)]ϕw=12(qbibkϕbk+qbibk+1ϕbk+1)\begin{aligned} \boldsymbol{\omega}^b & =\frac{1}{2}\left[\left(\boldsymbol{\omega}^{b_k}-\mathbf{b}_k^g\right)+\left(\boldsymbol{\omega}^{b_{k+1}}-\mathbf{b}_k^g\right)\right] \\ \boldsymbol{\phi}^w & =\frac{1}{2}\left(\mathbf{q}_{b_i b_k} \boldsymbol{\phi}^{b_k}+\mathbf{q}_{b_i b_{k+1}} \boldsymbol{\phi}^{b_{k+1}}\right) \end{aligned} ωbϕw=21[(ωbk−bkg)+(ωbk+1−bkg)]=21(qbibkϕbk+qbibk+1ϕbk+1)那么预积分的离散形式可以表示为
αbibk+1=αbibk+ϕwδtqbibk+1=qbibk⊗[112ωbδt]\begin{aligned} & \boldsymbol{\alpha}_{b_i b_{k+1}}=\boldsymbol{\alpha}_{b_i b_k}+\boldsymbol{\phi}^w \delta t \\ & \mathbf{q}_{b_i b_{k+1}}=\mathbf{q}_{b_i b_k} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \boldsymbol{\omega}^b \delta t \end{array}\right] \end{aligned} αbibk+1=αbibk+ϕwδtqbibk+1=qbibk⊗[121ωbδt]此时状态更新的公式可以整理为
[pwbjqwbjbjgj]=[pwbi+qwbiαbibjqwbiqbibjbig]\left[\begin{array}{c} \mathbf{p}_{w b_j} \\ \mathbf{q}_{w b_j} \\ \mathbf{b}_j^{g_j} \end{array}\right]=\left[\begin{array}{c} \mathbf{p}_{w b_i}+\mathbf{q}_{w b_i} \boldsymbol{\alpha}_{b_i b_j} \\ \mathbf{q}_{w b_i} \mathbf{q}_{b_i b_j} \\ \mathbf{b}_i^g \end{array}\right] pwbjqwbjbjgj=pwbi+qwbiαbibjqwbiqbibjbig残差形式可以写为
[rprqrbg]=[qwbi∗(pwbj−pwbi)−αbbbbj2[qbibj∗⊗(qwbi∗⊗qwbj)]xyzbjg−big]\left[\begin{array}{c} \mathbf{r}_p \\ \mathbf{r}_q \\ \mathbf{r}_{b g} \end{array}\right]=\left[\begin{array}{c} \mathbf{q}_{w b_i}^*\left(\mathbf{p}_{w b_j}-\mathbf{p}_{w b_i}\right)-\boldsymbol{\alpha}_{b_{b^b} b_j} \\ 2\left[\mathbf{q}_{b_i b_j}^* \otimes\left(\mathbf{q}_{w b_i}^* \otimes \mathbf{q}_{w b_j}\right)\right]_{x y z} \\ \mathbf{b}_j^g-\mathbf{b}_i^g \end{array}\right] rprqrbg=qwbi∗(pwbj−pwbi)−αbbbbj2[qbibj∗⊗(qwbi∗⊗qwbj)]xyzbjg−big其余部分(方差递推、残差对状态量雅可比、bias更新等)的推导,留作作业(仅优秀标准需要做)。
相关文章:

多传感器融合定位十三-基于图优化的建图方法其二
多传感器融合定位十二-基于图优化的建图方法其二3.4 预积分方差计算3.4.1 核心思路3.4.2 连续时间下的微分方程3.4.3 离散时间下的传递方程3.5 预积分更新4. 典型方案介绍4.1 LIO-SAM介绍5. 融合编码器的优化方案5.1 整体思路介绍5.2 预积分模型设计Reference: 深蓝学院-多传感…...
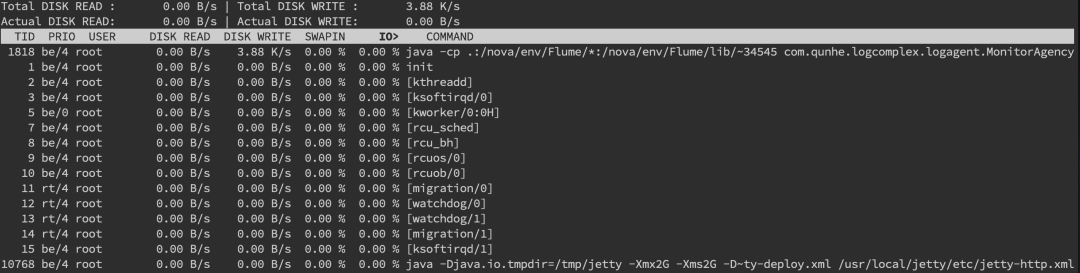
linux 服务器线上问题故障排查
一 线上故障排查概述 1.1 概述 线上故障排查一般从cpu,磁盘,内存,网络这4个方面入手; 二 磁盘的排查 2.1 磁盘排查 1.使用 df -hl 命令来查看磁盘使用情况 2.从读写性能排查:iostat -d -k -x命令来进行分析 最后一列%util可以看到每块磁盘写入的程度,而rrqpm/s以及…...

Sandman:一款基于NTP协议的红队后门研究工具
关于Sandman Sandman是一款基于NTP的强大后门工具,该工具可以帮助广大研究人员在一个安全增强型网络系统中执行红队任务。 Sandman可以充当Stager使用,该工具利用了NTP(一个用于计算机时间/日期同步协议)从预定义的服务器获取并…...
【SSL/TLS】准备工作:HTTPS服务器部署:Nginx部署
HTTPS服务器部署:Nginx部署1. 准备工作2. Nginx服务器YUM部署2.1 直接安装2.2 验证3. Nginx服务器源码部署3.1 下载源码包3.2 部署过程4. Nginx基本操作4.1 nginx常用命令行4.2 nginx重要目录1. 准备工作 1. Linux版本 [rootlocalhost ~]# cat /proc/version Li…...
微搭低代码从入门到精通11-数据模型
学习微搭低代码,先学习基本操作,然后学习组件的基本使用。解决了前端的问题,我们就需要深入学习后端的功能。后端一般包括两部分,第一部分是常规的数据库的操作,包括增删改查。第二部分是业务逻辑的编写,在…...

【算法基础】前缀和与差分
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法💪种一棵树最好是十年前其次是现在1.什么是前缀和前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身&#x…...
LTD212次升级 | 官网社区支持PC端展示 • 官网新增证件查询应用,支持条形码扫码查询
1、新增证件查询应用,支持条形码扫码查询; 2、新增用户社区PC端功能; 01证件查询应用 1、新增证件查询应用功能 支持证件信息录入、打印功能,支持条形码扫码识别。 后台管理操作路径:官微中心 - 应用 - 证件查询 …...
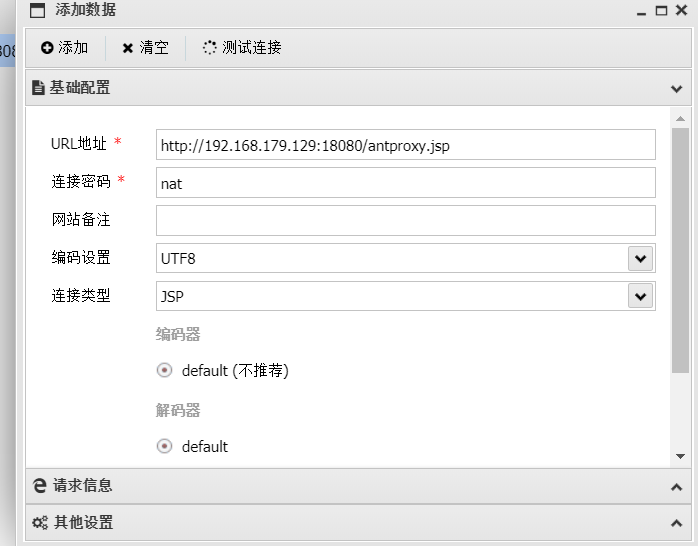
【安全】nginx反向代理+负载均衡上传webshell
目录 一、负载均衡反向代理下上传webshell Ⅰ、环境搭建 ①下载蚁剑,于github获取官方版: ②下载docker&docker-compose ③结合前面启动环境 ④验证 负载均衡下webshell上传 一、负载均衡反向代理下上传webshell 什么是反向代理? 通常的代…...
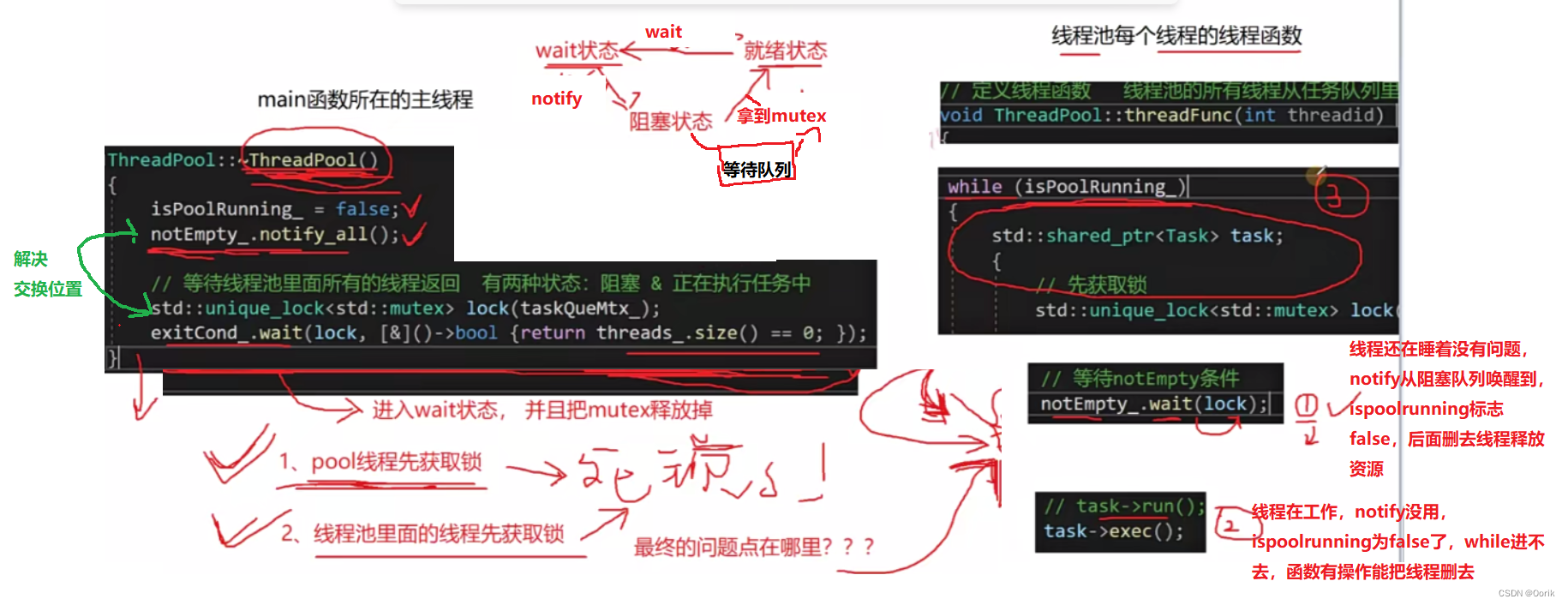
线程池框架
这是之前有做的一个可以接受用户传入任意类型的任务函数和任意参数,并且能拿到任务对应返回值的一个线程池框架,可以链接成动态库,用在相关项目里面。一共实现了两版,都是支持fixed和cached模式的,半同步半异步的&…...

【TCP的拥塞控制】基于窗口的拥塞控制
TCP的拥塞窗口CWND大小和传输轮次n的关系如下所示。(本题10分) cwnd12481632333435363738394041422122232425261248N1234567891011121314151617181920212223242526 问题: (1)慢开始阶段的时间间隔?&#…...
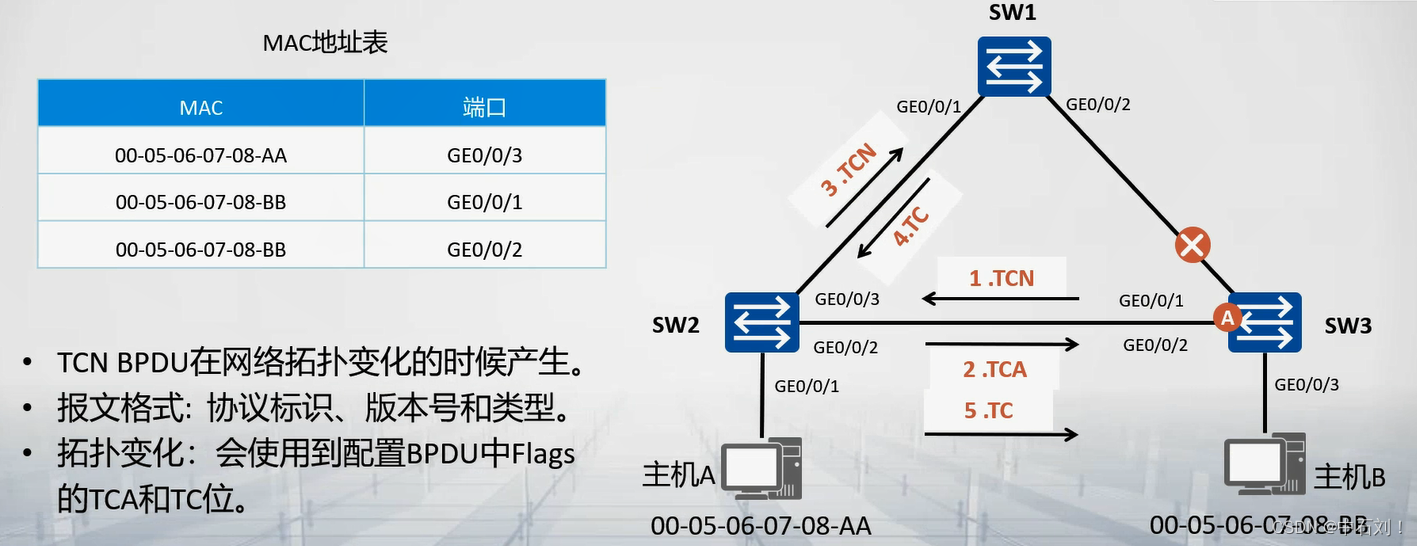
STP协议基础
STP协议技术来源二层环路及危害二层交换机网络的冗余性与环路人为错误导致的二层环路二层环路带来的问题STP生成树协议STP概述STP基本概念桥ID根桥COSTRPC(Root Path Cost)根路径开销PORT ID端口IDBPDU桥协议数据单元STP的计算过程(1…...
Linux上面配置Apache2支持Https(ssl)具体方案实现
虽然Nginx比较流行,但是由于一些老项目用到了Apache2来支持Web服务,最近想给服务上一个Https支持,虽然看似教程简单,但是也遇到一些特殊情况,经历了一番折腾也算是解决了所有问题,将过程记录如下。演示是基…...
[Linux]进程替换
🥁作者: 华丞臧. 📕专栏:【LINUX】 各位读者老爷如果觉得博主写的不错,请诸位多多支持(点赞收藏关注)。如果有错误的地方,欢迎在评论区指出。 推荐一款刷题网站 👉 LeetCode刷题网站 文…...

常见的锁策略面试题
你是怎么理解乐观锁和悲观锁的,具体怎么实现呢? 悲观锁认为多个线程访问同一个共享变量冲突的概率较大, 会在每次访问共享变量之前都去真正加锁 乐观锁认为多个线程访问同一个共享变量冲突的概率不大. 并不会真的加锁, 而是直接尝试访问数据. 在访问的…...
设计师一定要知道这几个网站,解决你80%的设计素材。
本期推荐一波设计师必备的设计素材网站,设计党赶紧马住!能解决你日常设计中80%的素材。 1、菜鸟图库 菜鸟图库-免费设计素材下载 这是一个为新手设计师提供免费素材的设计网站,站内有超多平面模板、海报、UI设计、电商设计等相关素材&#x…...
QT基础入门
学习视频:QT开发概述_哔哩哔哩_bilibili 1.QT开发概述 1.什么是QT QT是一个1991年由Qt Company开发的跨平台C图形用户界面应用程序开发框架。它既可以开发GUI程序,也可用于开发非GUI程序,比如控制台工具和服务器。Qt是面向对象的框架&#…...

高数不定积分72题解答
题目来源:这72道积分题目会积了,绝对是高高手 作者: 湖心亭看雪 第一题 原式∫15x3dx15∫15x3d(5x3)15ln(5x3)C\begin{aligned} \text{原式}&\int \frac{1}{5x3}dx \\ &\frac{1}{5} \int\frac{1}{5x3}d(5x3) \\ &\frac{1}{5} ln…...
基于北方苍鹰算法优化LSTM(NGO-LSTM)研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Linux内核启动(理论,0.11版本)分段与分页
为什么要虚拟内存 我们知道,在之前上微机原理时,我们的程序是可以直接访问内存的,而且访问的是直接的物理内存,在实模式下,寄存器是16位的,数组总线(data bus)是16位的,…...

数据与C(字符串)
目录 一.概念引入 二.字符串(数组存储,必须以\0结尾) 三.错误示范 四.strlen()和sizeof()相对于字符串的不同 一.概念引入 “a”,a哪个是字符哪个又是字符串,嘿嘿不用猜了 我们在上一章中说过&#x…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
