红黑树-随记
文章目录
- 1.为什么hashmap用红黑树不用二叉树和平衡二叉树
- 1.1 二叉树(Binary Search Tree)
- 1.2 红黑树(Red Black Tree)
- 1.3 平衡二叉树(Balence Binary Tree)也称AVT
- 2.为什么mysql用b+数,不用B数或B*数作为存储引擎的数据结构?
- 2.1 B树
- 2.2 B+树
- 2.3.B*树
- 2.4.R树
- 2.5.树的演进
- 3.深入红黑树
- 3.1 旋转方式(4种)
- 3.1.1 节点左旋(节点下右侧子节点深度过长)
- 3.1.2 节点右旋(节点下的子节点左侧深度过长)
- 3.2 红黑树自平衡原则(何时触发左右旋及变色)重点
- 3.2.1.变色
- 3.2.2.左旋
- 3.2.3.右旋
- 3.2.4例子
- 3.2 插入自平衡(最多2次旋转)
- 3.3 删除自平衡(最多3次旋转)
1.为什么hashmap用红黑树不用二叉树和平衡二叉树
1.1 二叉树(Binary Search Tree)
特性:
1.每个节点最多有两颗子树,所以二叉树中不存在度大于2的节点;(度=子节点个数)
2.左子树和右子树是有序的,不能任意颠倒
3.即使一个节点只有一颗子树,也要区分是左子树还是右子树
缺点:极端情况下退化成链表,导致索引效率大大降低,也间接影响了删除性能。
1.2 红黑树(Red Black Tree)
红黑树的出现就是为了 解决二叉树退化成链表的问题;它是趋于平衡的树
1.3 平衡二叉树(Balence Binary Tree)也称AVT
特性
1.根节点左边的节点值必须小于根节点,根节点右边的节点值必须大于根节点;
2.每个节点的左右深度差值不能大于1;
缺点:由于节点深度差值不能大于1,所以在大量插入或删除的时候,会一直调整数的平衡,此时性能不如红黑树;原因是由于红黑树的可以容忍最大深度不能超过最小深度2倍,大量的插入和删除时,性能优于AVT。
2.为什么mysql用b+数,不用B数或B*数作为存储引擎的数据结构?
2.1 B树
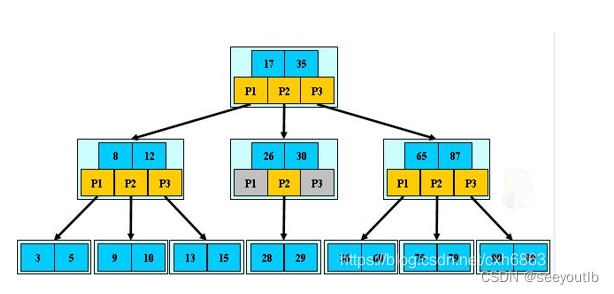
特点:
1.每个节点都存储key和value,所有节点组成这棵树,并且叶子节点的指针为null
2.任何一个关键字只出现在一个节点中;如key
3.搜索有可能在非叶子节点结束
4.在关键字全集做一次查找,性能逼近二分查找
2.2 B+树
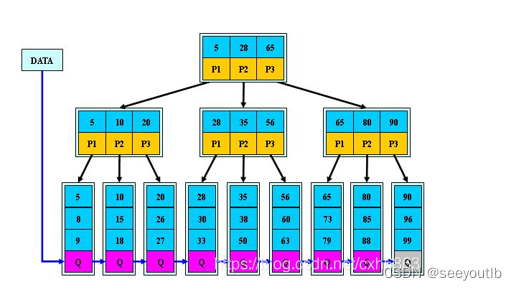
特点:
1.只有叶子节点存储数据,包含这颗数的所有索引值,叶子节点不存储指针
(非叶子节点只存储索引值,不存储实际的数据,并非真正的data)
2.增加了访问数据的指针,每个叶子节点增加一个指向相邻叶子节点的指针(范围查下性能大幅提升)
2.3.B*树
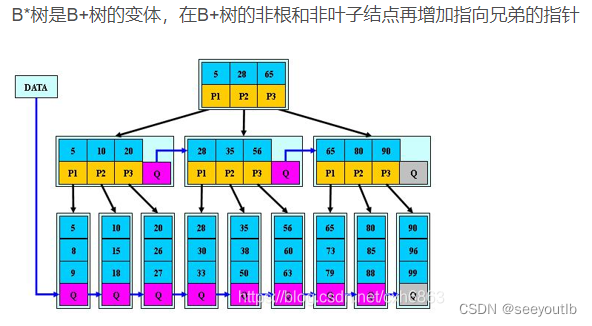
特点:B*树是对B+树的改进,在非叶子节点的兄弟之间增加了双向指针,目的优化B+数在叶子节点满而分裂时的效率;
构建过程对比:
B+树,在叶子节点数据满时,叶子就会分裂;
B*树,在叶子节点数据满时,会询问兄弟节点空间是否满,如果没满,则转移部分关键字;如果满了则每个兄弟节点拿出1/3数据创建新的节点
2.4.R树
R树特性:叶子节点会组多维空间层,查询时性能大幅降低,不再适合数据场景
2.5.树的演进
1、首先,为了保证树的节点均匀分布,所以在二叉树的基础上加上了平衡算法,就有了平衡二叉树。
2、为了减少树的高度,所以B树一个节点下面可以添加N个子节点,然后每个节点的大小限制在磁盘块容量大小,让节点只需要通过一次IO就能读取到所有数据,通过增加节点存储的数据减少了树的高度,而节点的数据变多并没有让IO次数变多。
3、B+树在B树的基础上,在查询的稳定性 和排序方面进行了优化,因为B+树所有的数据都会保存到叶子节点,然后所有叶子节点本身是有序的。
4、B*树为了减少 树在构建过程中节点的拆分、合并次数,所以在每个节点上都保存了旁边节点的指针,在节点需要进行拆分、合并时,优先从旁边节点挪数据,从而减少构建过程中节点拆分、合并的次数,提升了树的构建性能。
3.深入红黑树
优化:解决二叉树极端情况下退化成链表大大降低索引效率的问题
3.1 旋转方式(4种)
3.1.1 节点左旋(节点下右侧子节点深度过长)
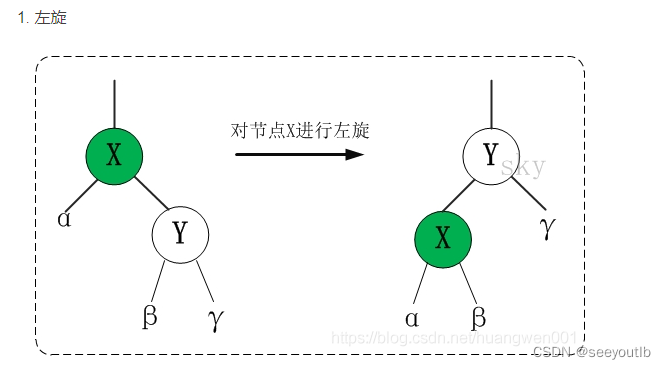
角色:
- 轴节点(旋转节点): X
- 被旋节点:Y
- 子节点:α(阿尔法)、β(贝塔)、γ(伽马)
左旋原理:
1.轴节点右侧子节点作为轴节点的父节点
2.原轴节点的左侧节点父节点和位置不变
3.原被旋节点右侧节点父节点和位置不变
4.轴节点右侧子节点的左侧子节点作为轴节点的右侧子节点
3.1.2 节点右旋(节点下的子节点左侧深度过长)
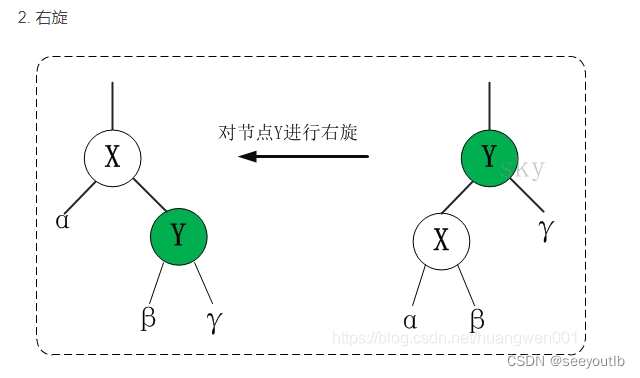
角色:
- 轴节点(旋转节点): Y
- 被旋节点:X
- 子节点:α(阿尔法)、β(贝塔)、γ(伽马)
右旋原理
1.轴节点的左侧子节点作为轴节点的父节点
2.轴节点右侧子节点父节点和位置不变
3.被旋节点左节点的父节点和位置不变
4.轴节点的左侧子节点作为被旋节点的右节点
左右旋小结:轴节点左子节点和被旋节点右子节点的父节点和位置不变
位置不变指的是:子节点旋转前和旋转后依然是父节点的左子节点或右子节点;如上图α和γ节点
3.2 红黑树自平衡原则(何时触发左右旋及变色)重点
旋转和变色规则:所有插入节点默认为红色
3.2.1.变色
条件:插入节点的父节点和叔叔节点为红色
步骤:
1.父节点和叔节点变为黑色
2.把祖父节点变为红色
3.把祖父节点作为插入节点
另外变色条件:红黑树为空时,插入当前节点,将当前节点变为黑色
3.2.2.左旋
条件:当前父节点为红色,叔叔为黑色,且当前节点为右子树
步骤:以父节点作为轴节点左旋
3.2.3.右旋
条件:当前父节点为红色,叔叔为黑色,且当前节点为左子树
步骤:
1.把父节点变为黑色
2.把祖父节点变为红色
3.以祖父节点右旋
3.2.4例子
1.插入节点62:
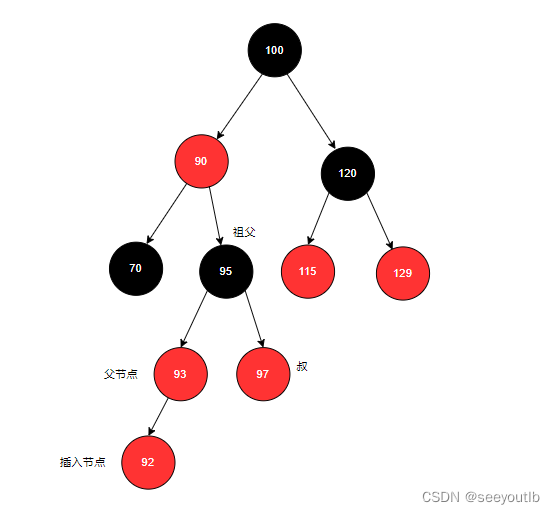
2.满足变色条件,进行变色。变色后如下
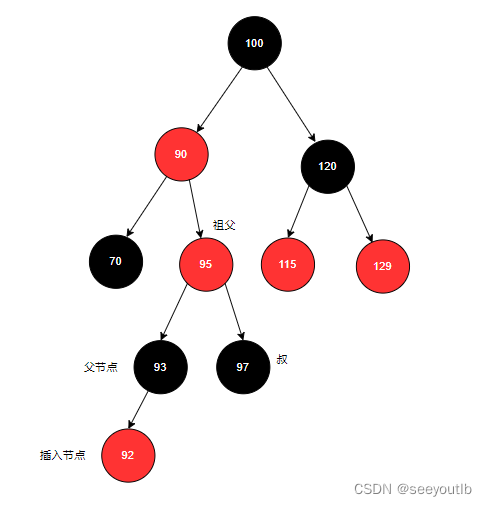
再将祖父节点作为插入节点,如下图:
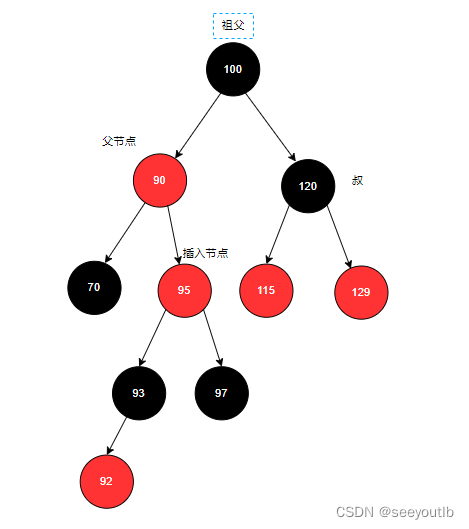
3.满足左旋条件:旋转后如下
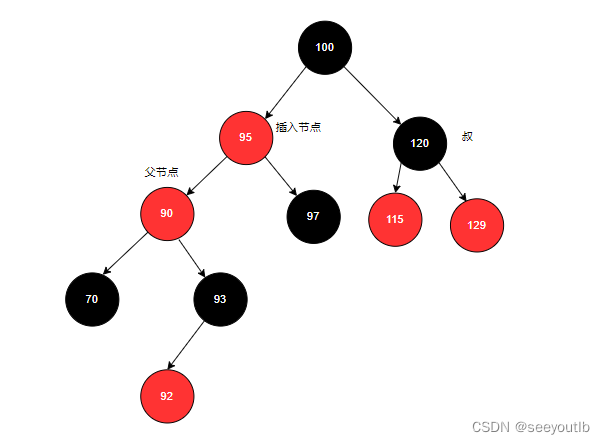
4.再以90作为插入节点,再次判断是否要变色或旋转
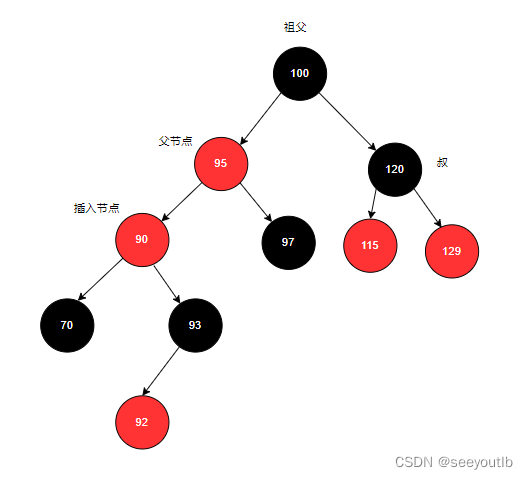
5.满足右旋条件:先变色,后旋转
先变色:变色后
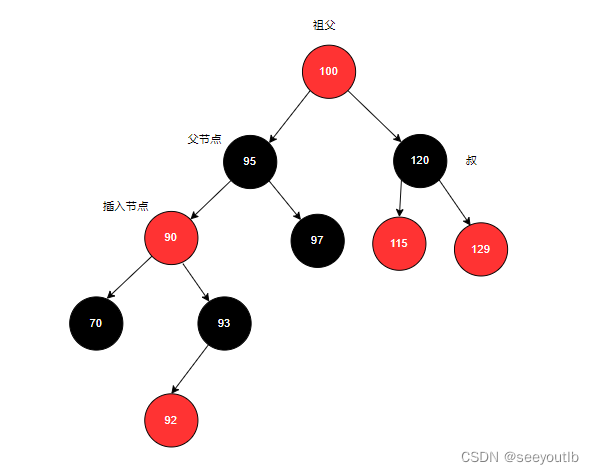
以祖父作为插入节点右旋:旋转后
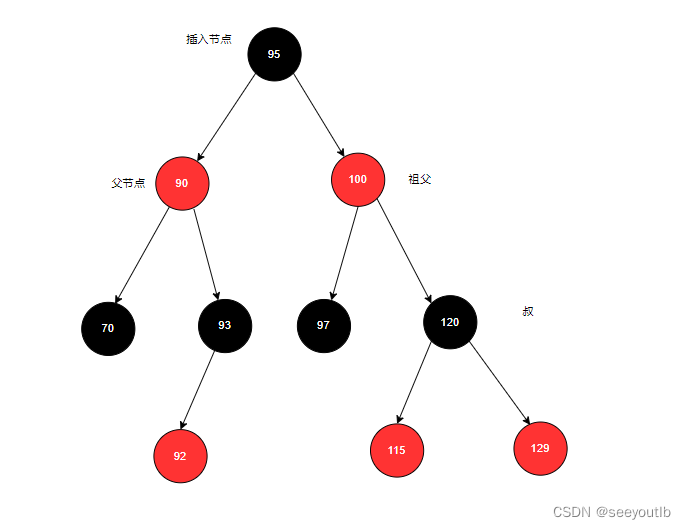
3.2 插入自平衡(最多2次旋转)
1.插入时,红黑树为空,插入节点变为黑色
2.插入时,父节点为黑色,直接插入
3.当父节点为红色时,情况有5种,惨遭上述变色左右旋规则循环直到满足红黑树性质
详情请看java-TreeMap或HashMap源码
java红黑树hashmp插入分析:
3.3 删除自平衡(最多3次旋转)
详情请看java-TreeMap或HashMap源码
相关文章:

红黑树-随记
文章目录1.为什么hashmap用红黑树不用二叉树和平衡二叉树1.1 二叉树(Binary Search Tree)1.2 红黑树(Red Black Tree)1.3 平衡二叉树(Balence Binary Tree)也称AVT2.为什么mysql用b数,不用B数或…...

Python异常处理更新,正常和不正常的都在这里
嗨害大家好鸭!我是小熊猫~ 异常处理篇嗨害大家好鸭!我是小熊猫~Python标准异常💨什么是异常?不正常异常处理💨使用except而不带任何异常类型使用except而带多种异常类型try-finally 语句异常的参数触发异常用户自定义异…...
[数据结构]:10-二叉排序树(无头结点)(C语言实现)
目录 前言 已完成内容 二叉排序树实现 01-开发环境 02-文件布局 03-代码 01-主函数 02-头文件 03-BinarySearchTreeCommon.cpp 04-BinarySearchTreeFunction.cpp 结语 前言 此专栏包含408考研数据结构全部内容,除其中使用到C引用外,全为C语言…...

openstack浅析
** OpenStack是一个由多个组件组成的开源云计算平台,每个组件都有不同的功能和用途。 ** 组件构成 以下是OpenStack中一些常见的组件及其功能: Nova:用于管理虚拟机的组件,提供了虚拟机的创建、销毁、管理等功能。 Neutron&am…...

华为OD机试Golang解题 - 特异性双端队列 | 含思路
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...
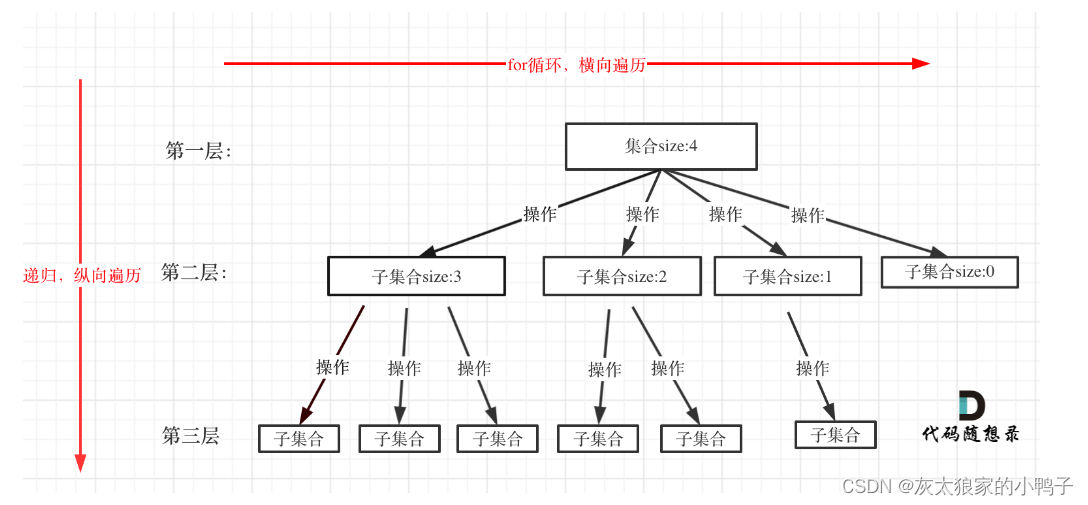
代码随想录中:回溯算法的基础
回溯算法是一种暴力的搜索方式;回溯法一般与递归同时存在。 回溯法,一般可以解决如下几种问题: 组合问题:N个数里面按一定规则找出k个数的集合切割问题:一个字符串按一定规则有几种切割方式子集问题:一个…...
Jetpack系列之LiveData)
Android kotlin 系列讲解(进阶篇)Jetpack系列之LiveData
<<返回总目录 文章目录 一、LiveData是什么二、LiveData测试一、LiveData是什么 LiveData是Jetpack提供的一种响应式编程组件,它可以包括任何类型的数据,并在数据发生变化的时候通知给观察者。LiveData特别适合与ViewModel结合在一起使用,虽然它也可以单独在别的地方…...

如何判断有向无环图:构造有向无环图
拓扑序列:可以用来判断一个有向图是否有环! 拓扑排序可以判断有向图是否存在环。我们可以对任意有向图执行上述过程,在完成后检查A序列的长度。 若A序列的长度小于图中点的数量,则说明某些节点未被遍历,进而说明图中存…...

【2022.1.3】手脱压缩壳练习(含练习exe)
【2022.1.3】手脱压缩壳练习(含练习exe) 文章目录【2022.1.3】手脱压缩壳练习(含练习exe)0、简介1、单步跟踪法(#)方法介绍(0)练习exe下载(1)、查看源程序&am…...

【异或哈希】CF855 div3 F
感觉这道题跟之前有一题特别像,都是异或哈希感觉这种题应该很典,记录一下(66条消息) Codeforces Round #841 (Div. 2) and Divide by Zero【异或差分动态map维护】 2022 C. Even Subarrays_lamentropetion的博客-CSDN博客Problem - F - Codeforces题意&a…...

深度学习|改进两阶段鲁棒优化算法i-ccg
目录 1 主要内容 2 改进算法 2.1 CC&G算法的优势 2.2 i-CCG算法简介 3 结果对比 1 主要内容 自从2013年的求解两阶段鲁棒优化模型的列和约束生成算法(CC&G)被提出之后,基本没有实质性的创新,都是围绕该算法在各个领…...

C++11轻松打印本地时间
C11之前,想要获取时间并对其打印是有些困难的,因为C并没有标准时间库。想要对时间进行统计就需要调用C库,并且我们要考虑这样的调用是否能很好的封装到我们的类中。 C11之后,STL提供了 chrono 库,其让对时间的操作更加…...
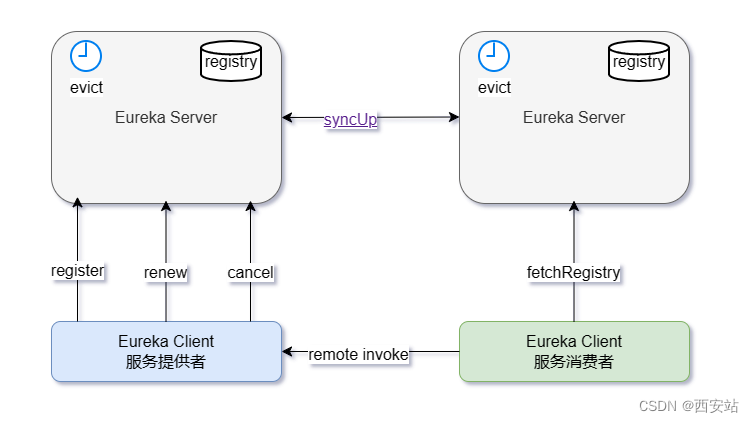
Eureka - 总览
文章目录前言架构注册中心 Eureka Server服务提供者 Eureka Client服务消费者 Eureka Client总结资源前言 微服务(Microservices,一种软件架构风格)核心的组件包括注册中心,随着微服务的发展,出现了很多注册中心的解决…...

【算法设计-枚举、分治】素数、约数、质因数分解
文章目录1. 素数判定2. 素数筛选法3. 质因数分解4. 求一个数的约数5. 求两个数的最大公约数(GCD)6. 求两个数的最小公倍数(LCM)1. 素数判定 判定从 2 到sqrt(n)依次能否把 n 整除,若存在可以整除的数则说明 n 不是素数…...
)
【第十四届蓝桥杯】第三期模拟赛B组C++题解(待修正+持续更新-ing)
文章目录写在前面一、找最小数题目描述解题报告1、大体思路2、代码详解二、求列名题目描述解题报告1、大体思路2、代码详解三、求日期数题目描述解题报告1、大体思路2、代码详解四、取数题目描述解题报告1、大体思路2、代码详解五、最大连通分块题目描述解题报告1、大体思路2、…...
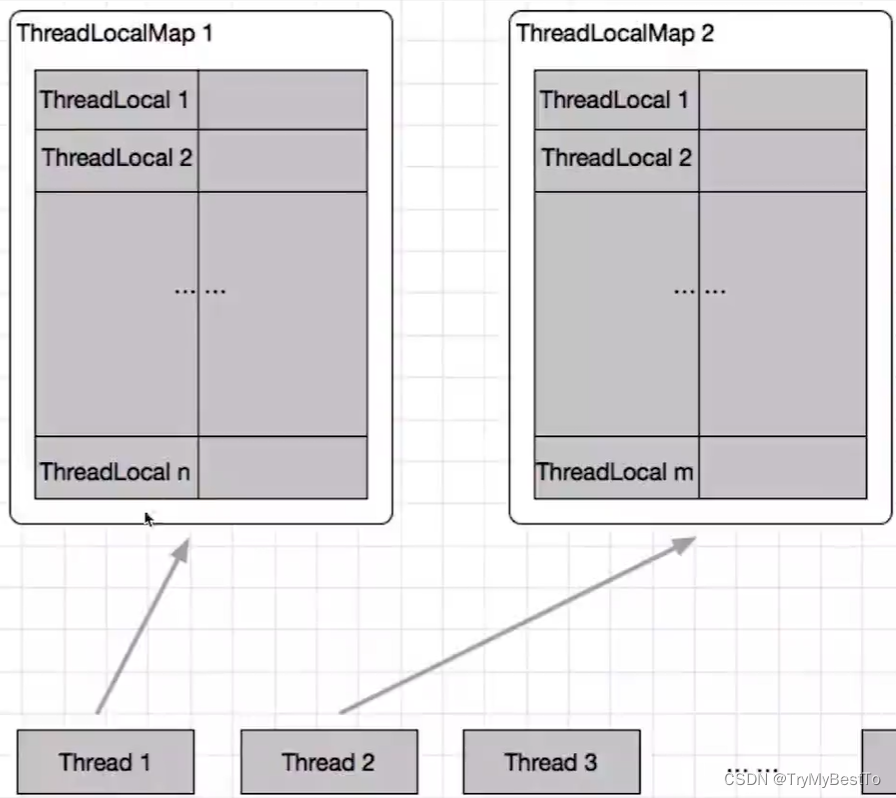
线程池和ThreadLocal详解
线程池和ThreadLocal详解线程池池化模式:线程池里的线程数量设定为多少比较合适?添加线程规则:实现原理:线程池实现任务复用的原理线程池状态:Executors 创线程池工具类手动创建(更推荐):自动创…...
)
[深入理解SSD系列综述 1.7] SSD固态存储市场发展分析与预测_固态存储技术发展方向(2022to2023)
前言 自2020年疫情爆发以来,远程办公、网上教育、流媒体等等应用引爆对消费电子及云服务的需求增长,全球数字化转型加速,带来了两年的闪存风光时刻。然而,进入2022年,在俄乌冲突、疫情重燃、通胀上升等一系列事件冲击下,全球经济下行风险加剧,对智能手机、PC等科技产品的…...
【2021.12.25】ctf逆向中常见加密算法和编码识别
【2021.12.25】ctf逆向中常见加密算法和编码识别(含exe及wp) 文章目录【2021.12.25】ctf逆向中常见加密算法和编码识别(含exe及wp)0、前言1、基础加密手法2、base64(1)原理:(2&#…...

【数据结构初阶】堆排序
目录 前言 概念 堆排序的实现 1.建堆 (1)堆向上调整算法 (2)堆的向下调整算法 2. 利用堆删除思想来进行排序 3.堆排序的时间复杂度 4.源码 总结 前言 前边我们学习了堆的实现,对堆的每个接口都进行了详细的讲…...

Day5: platformDriver-1
Platform Driver (1) Linux kernel中大部分设备可以归结为平台设备,因此大部分的驱动是平台驱动(patform driver) 什么是平台设备 平台设备是linux的设备模型中一类设备的抽象。 内核中的描述: Platform devices are devices t…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
