openssl3.2/test/certs - 041 - 1024-bit leaf key
文章目录
- openssl3.2/test/certs - 041 - 1024-bit leaf key
- 概述
- 笔记
- END
openssl3.2/test/certs - 041 - 1024-bit leaf key
概述
openssl3.2 - 官方demo学习 - test - certs
笔记
/*!
* \file D:\my_dev\my_local_git_prj\study\openSSL\test_certs\041\my_openssl_linux_doc041.txt
* \note openssl3.2/test/certs - 041 - 1024-bit leaf key
*/// --------------------------------------------------------------------------------
// official bash script
// --------------------------------------------------------------------------------
# openssl3.2/test/certs - 041 - 1024-bit leaf key
OPENSSL_KEYBITS=1024 ./mkcert.sh genee server.example ee-key-1024 ee-cert-1024 ca-key ca-cert// --------------------------------------------------------------------------------
// openssl cmd line parse
// --------------------------------------------------------------------------------
// cmd 1
openssl genpkey -algorithm rsa -pkeyopt rsa_keygen_bits:1024 -out ee-key-1024.pem// cmd 2
// cfg_exp041_cmd2.txt
string_mask=utf8only
[req]
prompt = no
distinguished_name = dn
[dn]
CN = server.exampleopenssl req -new -sha256 -key ee-key-1024.pem -config cfg_exp041_cmd2.txt -out req_exp041_cmd2.pem// cmd 3
// cfg_exp041_cmd3.txt
subjectKeyIdentifier = hash
authorityKeyIdentifier = keyid, issuer
basicConstraints = CA:falseextendedKeyUsage = serverAuth
[alts]
subjectAltName = @alts
DNS=server.exampleopenssl x509 -req -sha256 -out ee-cert-1024.pem -extfile cfg_exp041_cmd3.txt -CA ca-cert.pem -CAkey ca-key.pem -set_serial 2 -days 36525 -in req_exp041_cmd2.pem// --------------------------------------------------------------------------------
// openssl log
// --------------------------------------------------------------------------------
openssl genpkey -algorithm rsa -pkeyopt rsa_keygen_bits:1024 -out ee-key-1024.pem
openssl req -new -sha256 -key ee-key-1024.pem -config /dev/fd/63 -config /dev/fd/63 => /home/lostspeed/openssl/openssl-3.2.0_debian/test/certs/my_openssl_linux_log.txtstring_mask=utf8only
[req]
prompt = no
distinguished_name = dn
[dn]
CN = server.example
openssl x509 -req -sha256 -out ee-cert-1024.pem -extfile /dev/fd/63 -CA ca-cert.pem -CAkey ca-key.pem -set_serial 2 -days 36525 -extfile /dev/fd/63 => /home/lostspeed/openssl/openssl-3.2.0_debian/test/certs/my_openssl_linux_log.txtsubjectKeyIdentifier = hash
authorityKeyIdentifier = keyid, issuer
basicConstraints = CA:falseextendedKeyUsage = serverAuth
[alts]
subjectAltName = @alts
DNS=server.example[alts]END
相关文章:

openssl3.2/test/certs - 041 - 1024-bit leaf key
文章目录 openssl3.2/test/certs - 041 - 1024-bit leaf key概述笔记END openssl3.2/test/certs - 041 - 1024-bit leaf key 概述 openssl3.2 - 官方demo学习 - test - certs 笔记 /*! * \file D:\my_dev\my_local_git_prj\study\openSSL\test_certs\041\my_openssl_linux_…...

「创新引领未来」科东软件荣获第十二届中国创新创业大赛(广东·广州赛区)优胜奖
近日,广州市科学技术局公布第十二届中国创新创业大赛(广东广州赛区)暨2023年广州科技创新创业大赛常规赛拟获奖企业名单。科东软件凭借国产化技术创新优势、强大的应用场景落地能力和丰富的行业解决方案,荣获第十二届中国创新创业…...
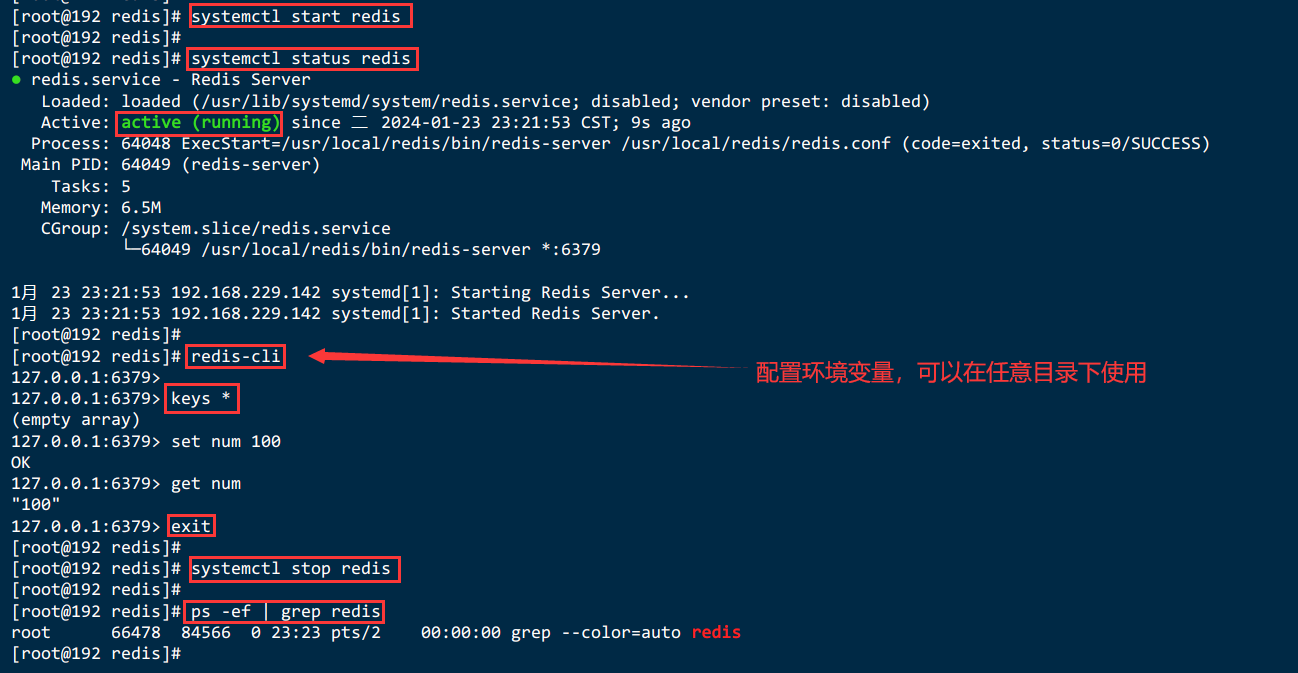
Linux下安装 Redis7
Linux下安装 Redis7 三、Linux下安装 Redis7【redis-7.2.4.tar.gz】3.1.下载redis的安装包3.1.1.手动下载Redis压缩包并上传【redis-7.2.4.tar.gz】3.1.2.wget工具下载redis-7.2.4.tar.gz 3.2.将安装包进行解压缩3.3.进入redis的安装包3.4.检查是否有gcc 环境3.5.编译和安装并指…...

spire.doc合并word文档
文章目录 spire.doc合并word文档1. 引入maven依赖2. 需要合并的word3. 合并文档代码4. 合并结果 spire.doc合并word文档 1. 引入maven依赖 <repositories><repository><id>com.e-iceblue</id><name>e-iceblue</name><url>https://r…...

蓝桥杯官网填空题(01串的熵)
问题描述 答案提交 这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。 import java.util.*;public class Main {public static void main(String[] args) {for(double zero1;zero<2333…...

【CodeTop】TOP 100 刷题 51-60
文章目录 51. 缺失的第一个正数题目描述代码与解题思路 52. 训练计划 II题目描述代码与解题思路 53. 子集题目描述代码与解题思路 54. 最小覆盖子串题目描述代码与解题思路 55. 从前序与中序遍历序列构造二叉树题目描述代码与解题思路 56. 零钱兑换题目描述代码与解题思路 57. …...

k8s的图形化工具---rancher
rancher是一个开源的企业级多集群的k8s管理平台。 rancher和k8s的区别:都是为了容器的调度和编排系统。但是rancher不仅可以调度还可以管理整个k8s集群。 rancher自带监控(普罗米修斯) 实验部署 master01 20.0.0.32 node01 20.0.0.34 node02 20.0.0.35 test …...
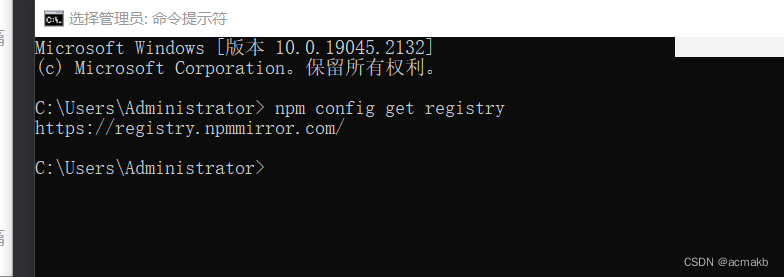
npm安装卡住问题(最新版)
npm安装卡住问题(最新版) 背景: 最近这两天用npm安装一些包的时候,发现一直卡住: 报错: idealTree:npm: sill idealTree buildDeps之前能用的现在不能用了,我一想,是不是源头的问题,还真是…...
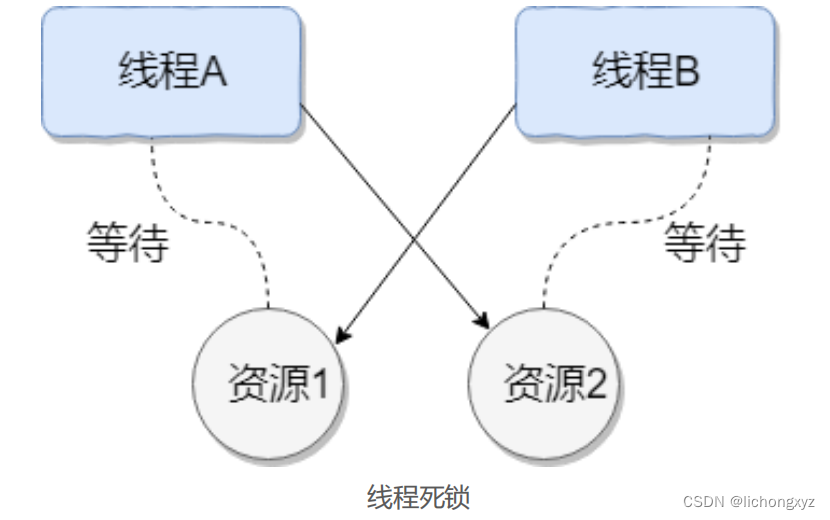
什么是线程死锁
死锁是指两个或两个以上的进程(线程)在执行过程中,由于竞争资 源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推 进下去。此时称系统处于死锁状态或系统产生了死锁,这些永远在互相…...
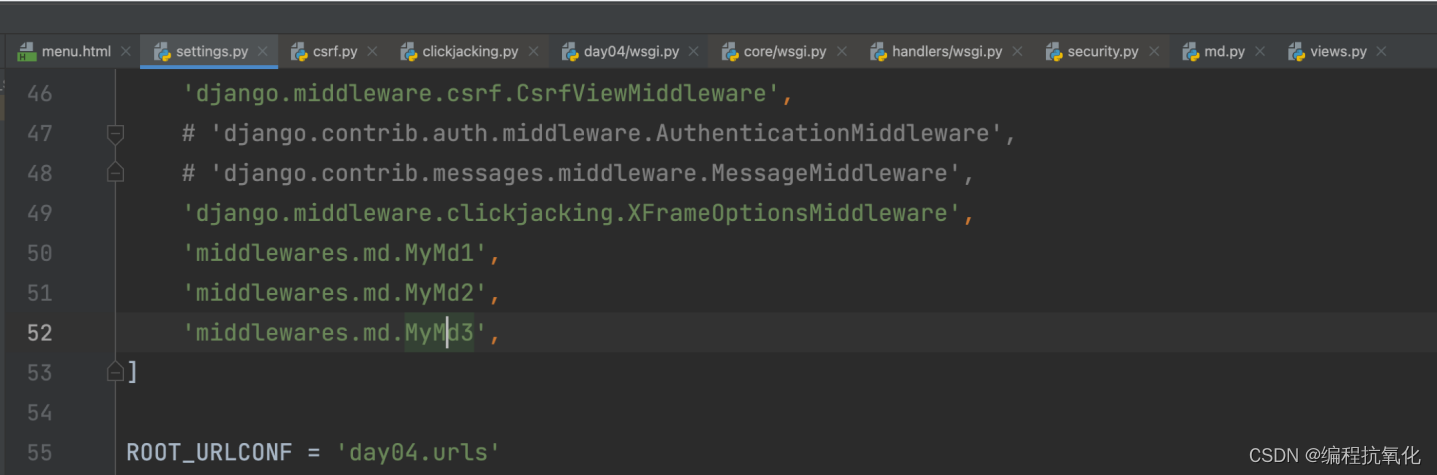
Django从入门到精通(二)
目录 三、视图 3.1、文件or文件夹 3.2、相对和绝对导入urls 3.3、视图参数requests 3.4、返回值 3.5、响应头 3.6、FBV和CBV FBV 四、静态资源 4.1、静态文件 4.2、媒体文件 五、模板 5.1、寻找html模板 5.2、模板处理的本质 5.3、常见模板语法 5.4、内置模板函…...

建筑物防雷检测安全接地应用解决方案
雷电是一种自然现象,具有极高的电压和电流,对建筑物及其内部设备、人员和财产可能造成严重的危害,如火灾、爆炸、电击、电磁干扰等。因此,建筑物必须采取有效的防雷措施,以保障建筑物的安全和可靠运行。建筑物防雷检测…...
支付宝小程序开发踩坑笔记(支付宝、学习强国小程序)
1、接口请求安卓端回调 success,IOS 端回调 fail 原因:dataType 设置不对,默认是 json 格式,对返回数据会进行 json 解析,如果解析失败,就会回调 fail 。加密传输一般是 text 格式。 2、input 禁止输入空格…...
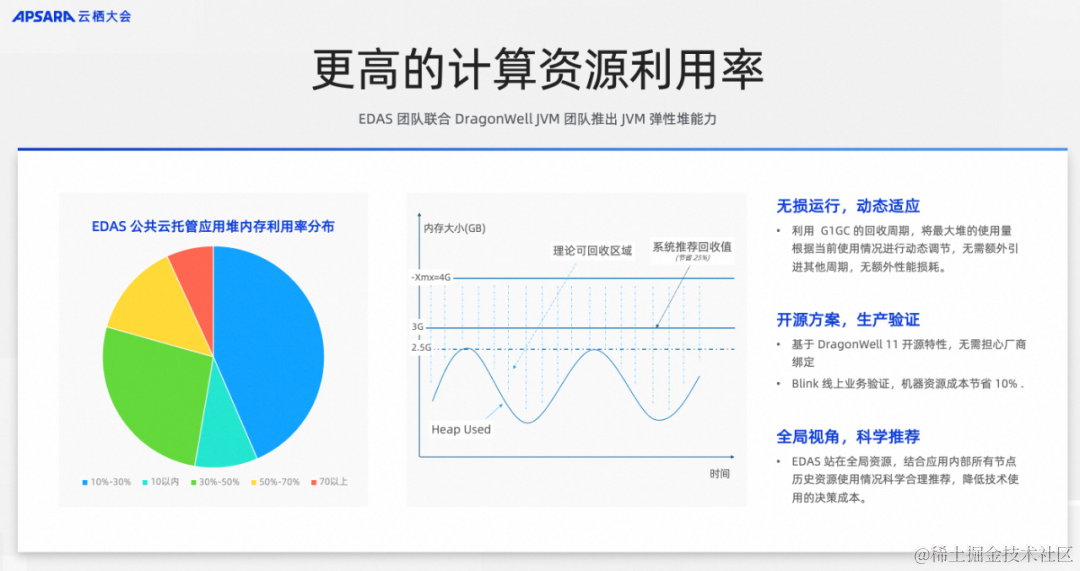
如何降低微服务复杂度丨云栖大会微服务主题分享实录
作者:谢吉宝 本文整理自阿里云资深技术专家、中间件负责人谢吉宝在2023云栖大会《极简微服务模式,降低微服务复杂度的最佳实践》的分享 2023 云栖大会现场 当面临复杂的挑战时,"分而治之"的方法往往能取得显著的效果。微服务架构…...

openresty 安装, nginx与 openresty
openresty VS nginx Nginx 是一款高性能的 Web 服务器和反向代理服务器,具备基础的功能如HTTP服务、负载均衡、反向代理以及动静分离等。它是许多互联网应用的核心组件,因其模块化和可扩展的设计而受到欢迎。1 OpenResty 是基于 Nginx 的 Web 平台&…...

puppeteer实现截图
Window服务器说明 1.在本地安装 puppeteer 先创建一个本地文件夹puppeteer,我的地址D:\common_workspace\puppeteer 然后使用cmd打开这个文件夹所在位置,再执行如下两条命令即可。 npm install -g cnpm --registryhttps://registry.npm.taobao.orgcnpm …...
【2024Java面试突击】并发编程、线程池面试实战
前言 最近在更新面试突击专栏,我把每一篇将字数都尽量控制在 2000 字以内,可能在文章里边写的没有那么细致,主要是提供一些 问题 以及 回答的思路 ,以及 面试中可能忽略的漏洞 ,所以在看完文章之后,如果自…...
ASUS华硕无畏Pro15笔记本电脑(M6500QB,M6500QH)工厂模式原厂OEM预装Windows11.22H2系统 含Recovery恢复
原装出厂Windows11系统适用于华硕无畏15笔记本电脑型号:M6500QB和M6500QH 链接:https://pan.baidu.com/s/1AVGLN6-ILIRogOMj48Mk1w?pwdmi7d 提取码:mi7d 带有ASUS RECOVERY恢复功能、自带所有驱动、出厂主题专用壁纸、系统属性联机支持…...

代码随想录算法训练营第三十天|51. N皇后
|51. N皇后 public List<List<String>> solveNQueens(int n) {List<List<String>> res new ArrayList<>();return null;}void backtracking1(int n, int row, int[] columns) {// 是否在所有n行里都摆放好了皇后?if (row n) {count;// 找到了…...
Kubernetes(K8S)各种攻击方法
1. 准备工作 1.1. metarget使用 项目地址(教程):https://github.com/Metarget/metarget/blob/master/README-zh.md 注意:推荐在Ubuntu 18.04(推荐)安装。 1.1.1. 安装metarget git clone https://github.com/Metarget/metarget.git cd metarget/ sudo apt install pyt…...
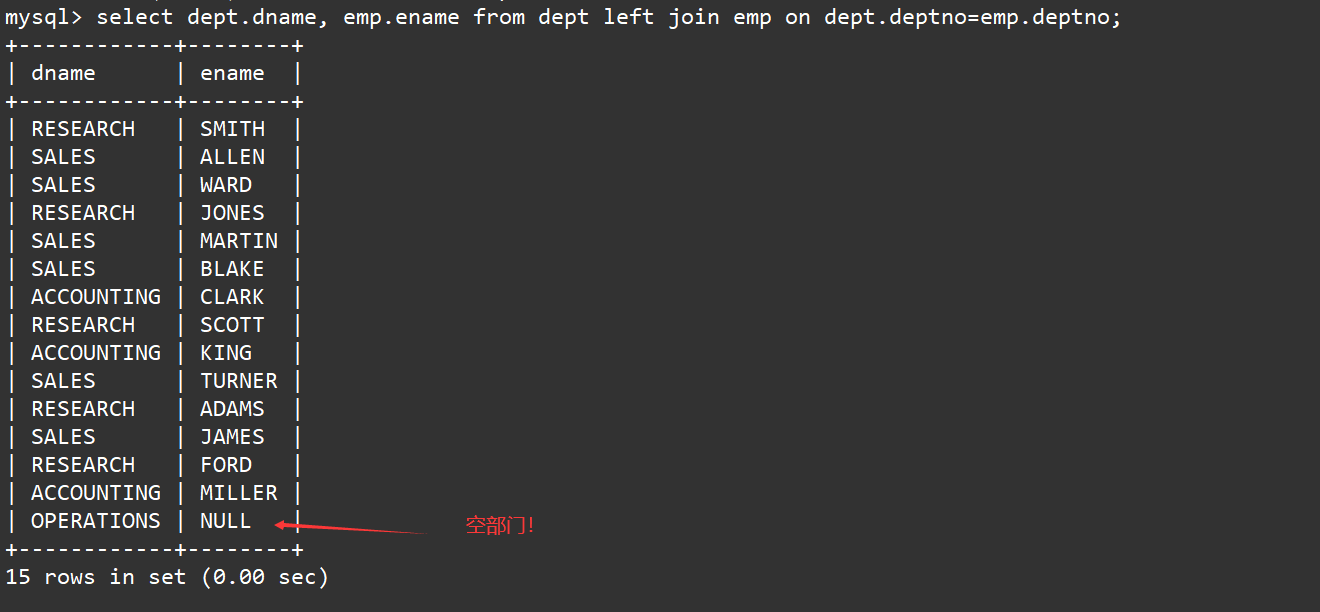
【MySQL】内外连接
内外连接 一、内连接二、外连接1、左外连接2、右外连接 表的连接分为内连和外连。 一、内连接 内连接实际上就是利用where子句对两种表形成的笛卡儿积进行筛选。只不过为了让sql的可读性更好,我们使用其他的关键字进行内连接。 语法: SELECT ... FRO…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
