c#算法(10)——求点到直线的距离
前言
在上位机软件开发领域,特别是机器视觉领域,经常会遇到尺寸测量的场景,比如让我们求一个点到一条直线的距离,我们已知了直线上的两个点的坐标,然后又已知了直线外的一个点的坐标,那么如何求出该直线外的一点到直线的距离呢?本文就是来讲解如何求点到直线的距离的,详细内容如下:
1、点到直线距离求解分析
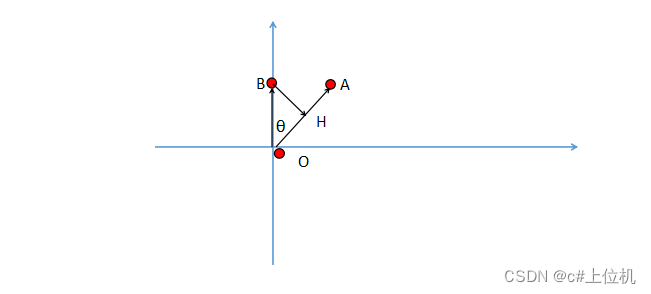
已知点O和点A为直线上的两个点,点B为经过OA两点所在直线外的一点,如果我们想求出B到OA的距离,那么过点B做一个垂线垂直于OA,交点为H,也就是说求点B到OA之间的距离,就是求BH的距离,并且BH的距离等于OB*sin(角BOA),由于点O和点B的坐标都是已知的,所以OB的长度就是已知的,所以只需要求出角BOA即可,又因为OB和OA都可以组成一个向量,并且点O、B、A坐标都是已知的,所以向量OB、OA都是已知的,所以就可以通过向量OA、OB求出这两个向量的夹角即可,关于如何求两个向量的夹角参考我的这篇博文求两个向量的夹角。
2 、点到直线距离C#源码实现
假设点O坐标为(0,0)
点A坐标为(2,2)
点B坐标为(0,2)
则到B到直线OA的距离等于1.4142,如下图;
相关文章:

c#算法(10)——求点到直线的距离
前言 在上位机软件开发领域,特别是机器视觉领域,经常会遇到尺寸测量的场景,比如让我们求一个点到一条直线的距离,我们已知了直线上的两个点的坐标,然后又已知了直线外的一个点的坐标,那么如何求出该直线外的一点到直线的距离呢?本文就是来讲解如何求点到直线的距离的,…...

[小脚本] maya 命令行常用操作
其实这些代码大部分是从 chatgpt 中生成的。 骨骼命名 import maya.cmds as cmdsdef rename_bones():selected_bones cmds.ls(type"joint") # 获取选中的骨骼for bone in selected_bones:if "_" in bone:new_name bone.split("_")[0] # 获…...
数据结构·单链表
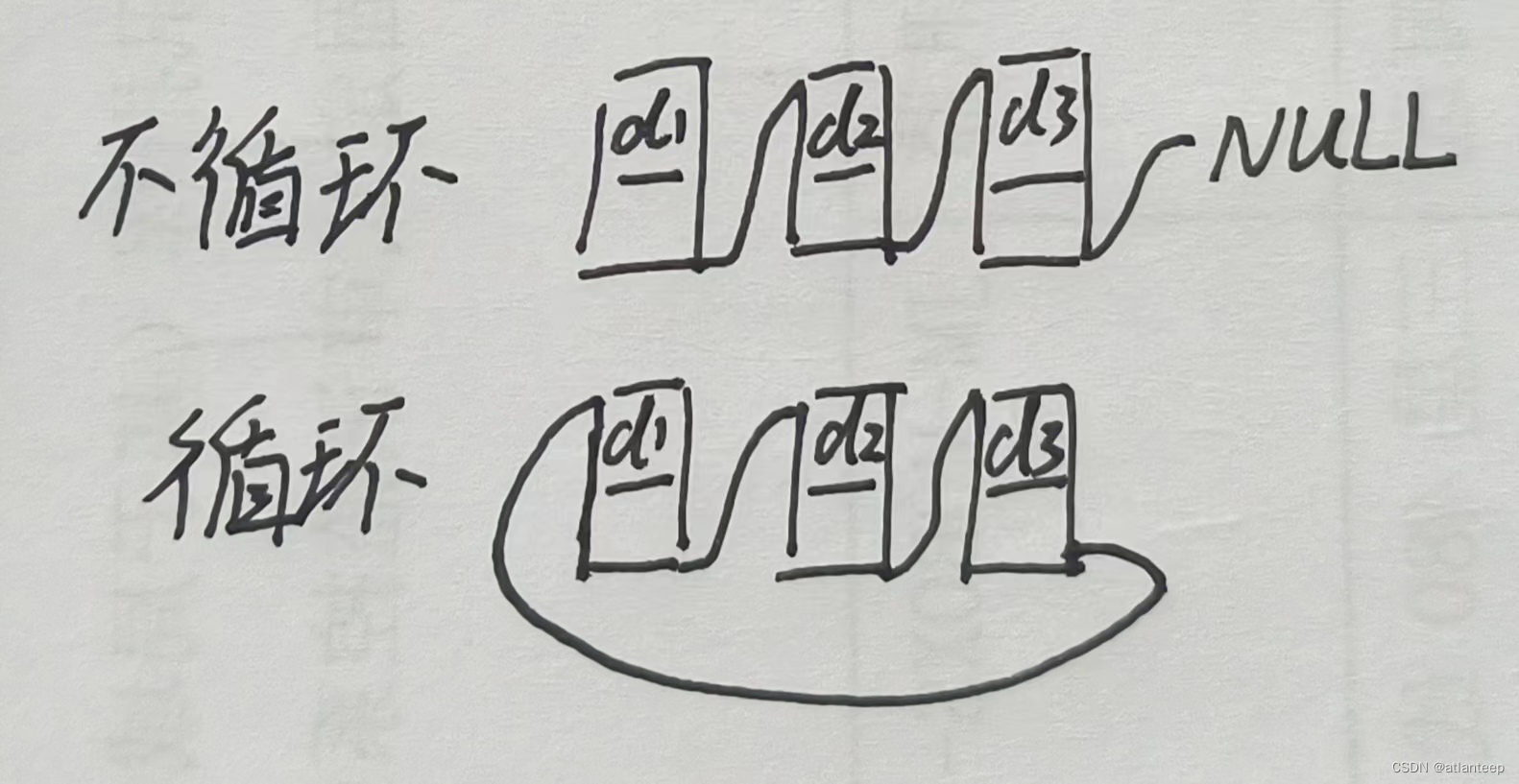
不可否认的是,前几节我们讲解的顺序表存在一下几点问题: 1. 中间、头部的插入和删除,需要移动一整串数据,时间复杂度O(N) 2. 增容需要申请新空间,拷贝数据,释放旧空间。会有不小的消耗 3. 增容一般是2倍的增…...

Redis(秒杀活动、持久化之RDB、AOF)
目录 秒杀活动 一、测压工具jmete的使用 二、java实现秒杀活动 1、myseckillcontroller 2、先启动pos请求添加商品,再启动jmeter进行压测 Redis持久化 一 、Redis持久化之RDB 1.RDB是什么 2. 备份是如何执行的 3.Fork 4. RDB持久化流程 5. dump.rdb文件 6…...
Window安装Python和开发Pycharm
准备: 1:安装Python环境 https://www.python.org/downloads/windows/ 2: 下载Pycharm https://www.jetbrains.com/pycharm/download/other.html...

技术驱动宠物健康:宠物在线问诊系统的高效搭建手册
在数字化时代,技术正在催生出许多创新的医疗服务,而宠物在线问诊系统便是其中一项引领潮流的创举。本文将为你提供一份高效搭建宠物在线问诊系统的手册,通过技术代码示例,让你轻松打造一套技术驱动的宠物健康管理系统。 1. 架构…...

玩转k8s:yaml介绍
一.Yaml文件详解 1.Yaml文件格式 (1)Kubernetes 支持 YAML 和 JSON 格式管理资源对象 (2)JSON 格式:主要用于 api 接口之间消息的传递 (3)YAML 格式:用于配置和管理,…...

【spdk】spdk compressdev测试
spdk-23.09\go\rpc\README.md go client 启应用 启哪个应用? ./build/bin/iscsi_tgt --wait-for-rpc & /usr/local/daos-2.4/prereq/release/spdk/share/spdk/scripts/rpc.py bdev_malloc_create -b Malloc0 1024 4096 #1G bs4k /usr/local/daos-2.4/prereq…...
Linux中并发程序设计(进程的创建和回收、exec函数使用)
进程的创建和回收 进程概念 概念 程序 存放在磁盘上的指令和数据的有序集合(文件) 静态的 进程 执行一个程序所分配的资源的总称 动态的进程和程序比较 注:进程是存在RAM中,程序是存放在ROM(flash)中的进程内容 BSS段ÿ…...

2023年DevOps国际峰会暨 BizDevOps 企业峰会(DOIS北京站):核心内容与学习收获(附大会核心PPT下载)
随着科技的飞速发展,软件开发的模式和流程也在不断地演变。在众多软件开发方法中,DevOps已成为当下热门的软件开发运维一体化模式。特别是在中国,随着越来越多的企业开始认识到DevOps的价值,这一领域的研究与实践活动日益活跃。本…...

pdf 转html 在线预览和查询
方案一:pdf2htmlex package com.realize.controller;import cn.hutool.http.HttpUtil; import com.alibaba.fastjson2.JSONObject; import com.realize.util.MsgUtil; import com.realize.util.OssUtil; import com.realize.util.PdfConvertUtil; import com.reali…...
docker 体验怀旧游戏(魂斗罗等)
docker run --restart always -p 8081:80 --name fc-games -d registry.cn-hangzhou.aliyuncs.com/bystart/fc-games:latest ip:8081访问 jsnes: js制作了一个网页版的NES模拟,可以在网页上玩fc游戏 (gitee.com)...

JS中判断数据类型总结以及方法封装
判断数据类型封装方法: 1)type返回字符串类型 2)is开头返回Boolean类型 测试实例: JavaScript 判断数据类型的方式共有四种 typeofinstanceofconstructorObject.prototype.toString typeof typeof 操作符返回一个字符串,表示操…...

【Midjourney】绘画风格关键词
1.松散素描(Loose Sketch) "Loose sketch"(松散素描)通常指的是一种艺术或设计中的手绘风格,其特点是线条和形状的表现相对宽松、自由,没有过多的细节和精确度。这样的素描通常用于表达创意、捕捉概念或者作为设计的初步…...

教你如何低成本自建「幻兽帕鲁」服务器,快速一键部署
创建幻兽帕鲁服务器1分钟部署教程,阿里云和腾讯云均推出幻兽帕鲁服务器服务器和部署教程,4核16G和4核32G配置可选,阿腾云atengyun.com分享1分钟自建幻兽帕鲁Palworld服务器教程: 幻兽帕鲁服务器创建教程 幻兽帕鲁服务器官方推荐…...

拥抱社交电商浪潮:微信小程序商城崛起引领电商新风向-亿发
在经过多年的发展后,各大传统电商平台的流量增速基本上已经见顶。同时,新兴的带有社交性质的电商平台,如抖音、小红书和微信商城(小程序商城)等,使得传统中心化平台的流量关注度逐渐分散。由于中心化平台需…...
一个使用pyqt的word文档查重工具
一个使用pyqt的word文档查重工具 使用场景代码使用截图打包好的软件下载链接结尾 使用场景 有时我们在借鉴一篇文档之后还不想有太多重复,这个时候可以使用这个工具对两个word文档进行对比 代码 import sys from PyQt5.QtWidgets import QApplication, QMainWind…...

SpringCloud Alibaba Sentinel 与 SpringCloud Gateway 的限流有什么差别?(三种限流算法原理分析)
目录 一、Sentinel 与 Gateway 的限流有什么差别? 1.1、前置知识 - 四种常见的限流算法 1.1.1、Tips 1.1.2、计数器算法 1)固定窗口计数器算法 2)滑动窗口计数器算法 1.1.3、令牌桶算法 1.1.4、漏桶算法 1.2、解决问题 一、Sentinel…...

邦芒忠告:职场新人最需要避开的十大雷坑
职场人最害怕的就是踩雷进坑,很多新入职场的小白都会战战兢兢,生怕哪里不对,冒犯了哪一位,或者触犯了哪一条潜规则。害怕自己踩到雷,没有走好职场第一步。最近,单位进了几个新人,看到他们就想起…...

MySQL-进阶-索引
一、索引概述 1、介绍 2、有误索引搜索效率演示 3、优缺点 二、索引结构 1、B-Tree(多路平衡查找树) 2、BTree 3、Hash 三、索引分类 四、索引语法 1、语法 2、案例 五、SQL性能分析 1、查看执行频次 2、慢查询日志 3、show-profile 4、explain...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
