MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法
MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法。阻尼最小二乘法通常用于处理数值求解问题中的不稳定性和噪声。以下是一个简单的MATLAB代码示例,演示了机械臂逆运动学的阻尼最小二乘法求解:
% 机械臂参数
L1 = 1; % 机械臂长度
L2 = 1;% 目标位置
x_desired = 1;
y_desired = 1;% 初始猜测
theta = [0, 0];% 最小二乘法参数
lambda = 0.1; % 阻尼系数% 迭代次数
max_iterations = 100;for iter = 1:max_iterations% 正运动学,计算当前末端位置x_current = L1 * cos(theta(1)) + L2 * cos(theta(1) + theta(2));y_current = L1 * sin(theta(1)) + L2 * sin(theta(1) + theta(2));% 误差error = [x_desired - x_current; y_desired - y_current];% 雅可比矩阵J = [-L1 * sin(theta(1)) - L2 * sin(theta(1) + theta(2)), -L2 * sin(theta(1) + theta(2));L1 * cos(theta(1)) + L2 * cos(theta(1) + theta(2)), L2 * cos(theta(1) + theta(2))];% 阻尼最小二乘法求解delta_theta = pinv(J' * J + lambda^2 * eye(2)) * J' * error;% 更新关节角度theta = theta + delta_theta';% 判断是否达到目标精度if norm(error) < 1e-6break;end
end% 输出最终结果
disp('最终关节角度:');
disp(theta);
请注意,这只是一个简单的例子,实际应用中需要根据具体的机械臂结构和运动学方程进行调整。
相关文章:

MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法
MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法。阻尼最小二乘法通常用于处理数值求解问题中的不稳定性和噪声。以下是一个简单的MATLAB代码示例,演示了机械臂逆运动学的阻尼最小二乘法求解: % 机械臂参数 L1 1; % 机械臂长度 L2 1;…...
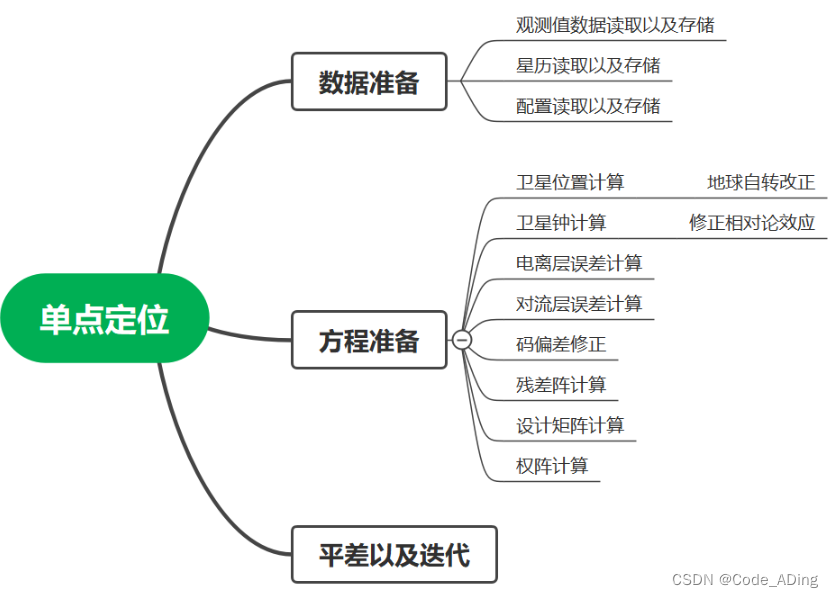
2024.1.24 GNSS 学习笔记
1.伪距观测值公式 2.载波相位观测值公式 3.单点定位技术(Single Point Positionin, SPP) 仅使用伪距观测值,不使用其他的辅助信息获得ECEF框架下绝对定位技术。 使用广播星历的轨钟进行定位,考虑到轨钟的米级精度,所以对于<1米的误差&…...
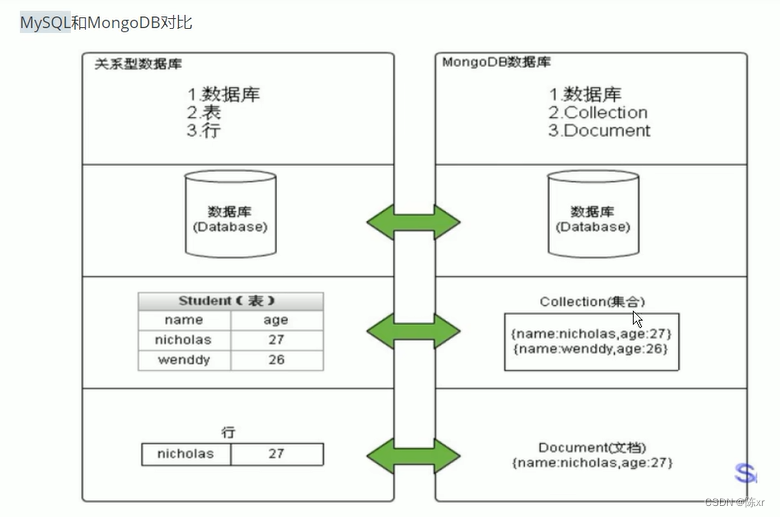
2024-01-22(MongoDB)
1.Mongodb使用的业务场景: 传统的关系型数据库/mysql在“三高”需求以及应对web2.0的网站需求面前,有点力不从心,什么是“三高”需求: a. 对数据库高并发的读写需求 b. 对海量数据的高效率存储和访问需求 c. 对数据库的高可扩…...
无人机航迹规划(六):七种元启发算法(DBO、LO、SWO、COA、LSO、KOA、GRO)求解无人机路径规划(提供MATLAB代码)
一、七种算法(DBO、LO、SWO、COA、LSO、KOA、GRO)简介 1、蜣螂优化算法DBO 蜣螂优化算法(Dung beetle optimizer,DBO)由Jiankai Xue和Bo Shen于2022年提出,该算法主要受蜣螂的滚球、跳舞、觅食、偷窃和繁…...
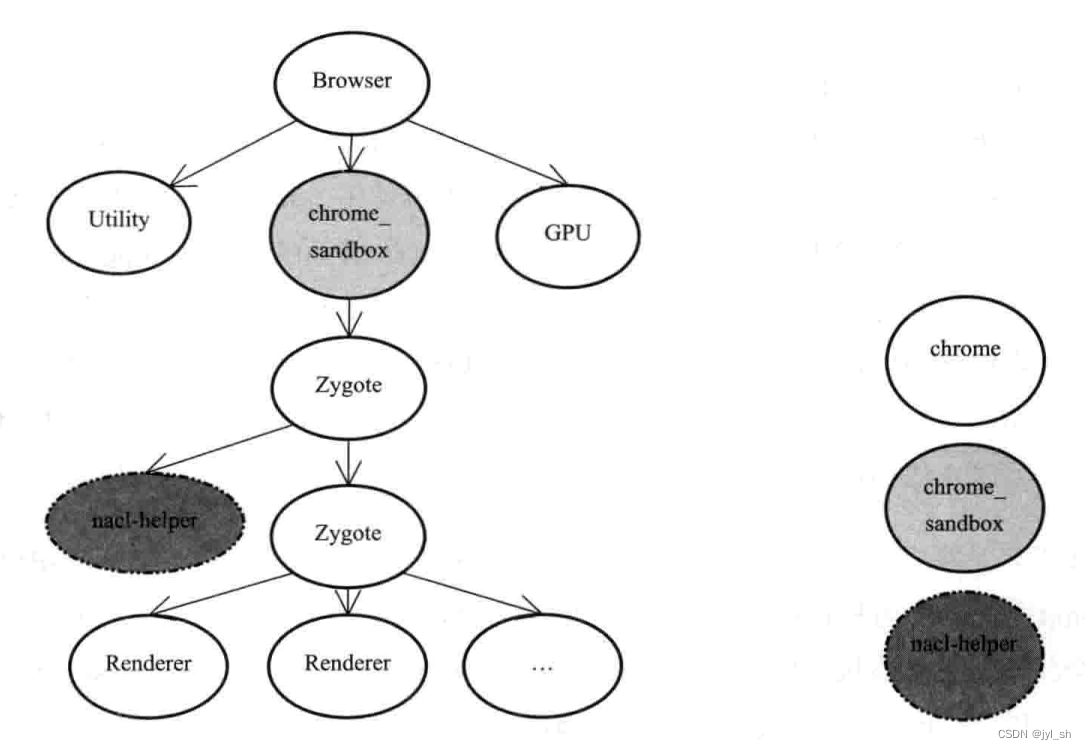
《WebKit 技术内幕》学习之十二(2):安全机制
2 沙箱模型 2.1 原理 一般而言,对于网络上的网页中的JavaScript代码和插件是不受信的(除非是经过认证的网站),特别是一些故意设计侵入浏览器运行的主机代码更是非常危险,通过一些手段或者浏览器中的漏洞,…...
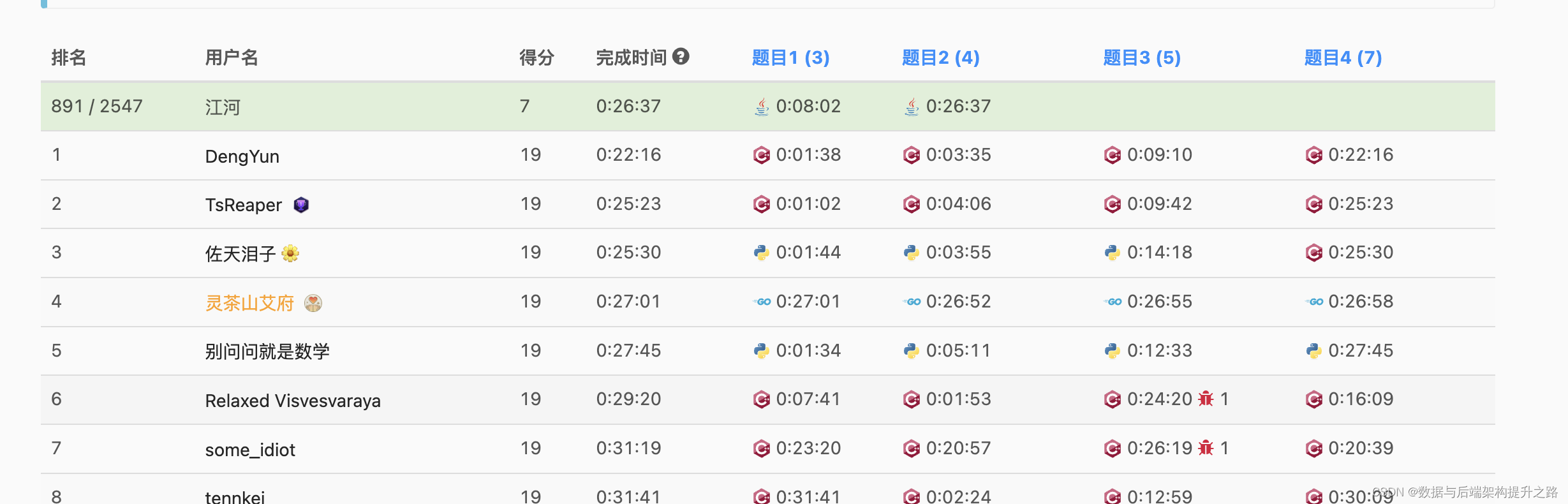
算法优化:LeetCode第122场双周赛解题策略与技巧
接下来会以刷常规题为主 ,周赛的难题想要独立做出来还是有一定难度的,需要消耗大量时间 比赛地址 3011. 判断一个数组是否可以变为有序 public class Solution {public int minimumCost(int[] nums) {if (nums.length < 3) {// 数组长度小于3时&a…...
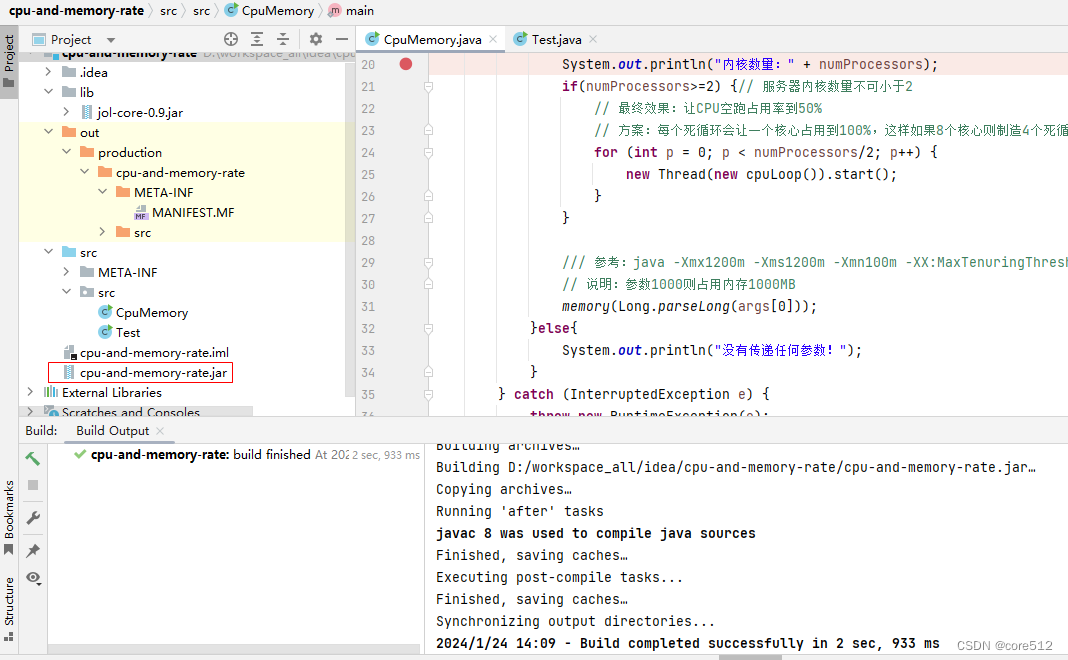
IDEA导出jar
1、选择导出方式 2、选择Main Class 3、构建jar...
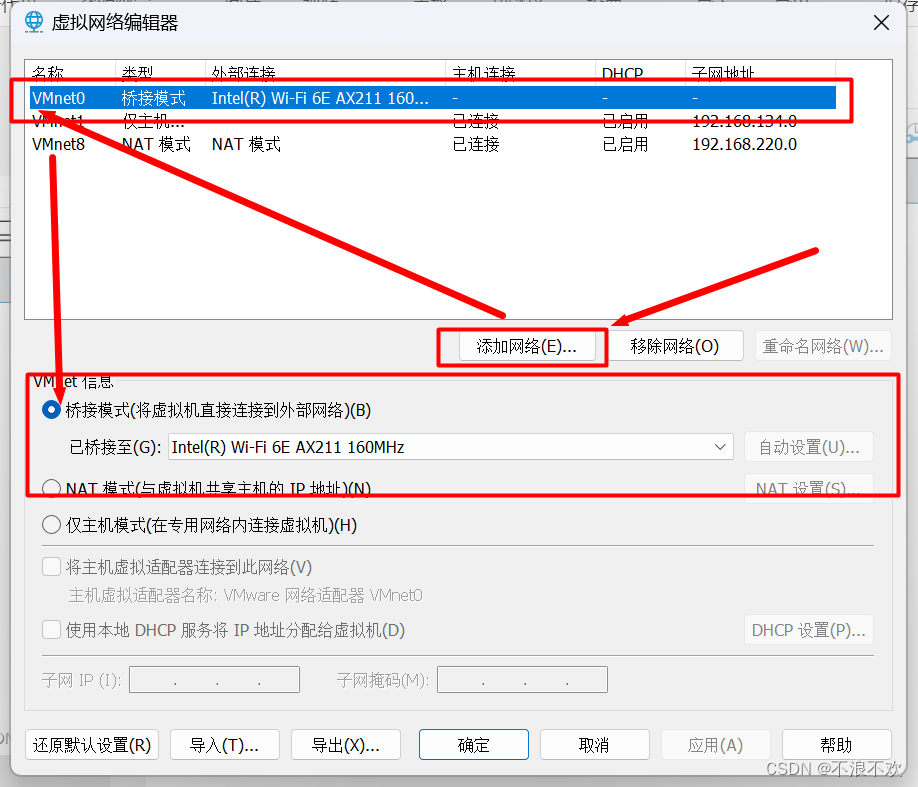
Win10/11中VMware Workstation设置网络桥接模式
文章目录 一、添加VMware Bridge Protocol服务二、配置桥接参数1.启用系统Device Install Service服务2.配置VMware 需要确认物理网卡是否有添加VMware Bridge Protocol服务 添加VMware Bridge Protocol服务 提示:以下是本篇文章正文内容,下面案例可供参…...

html Canvas粒子文字特效
代码有点长,下面是代码: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>HTML5 Canvas粒子效果文字动画特效DEMO演示</title><link rel"stylesheet" href"css/normalize.c…...

@JsonFormat失效,被jackson自定义配置覆盖
jackson配置类 我的jackson配置类如下,其中serializerByType(LocalDateTime.class, new LocalDateTimeSerializer()) 覆盖了JsonFormat注解 Configuration public class JacksonConfiguration {public static final DateTimeFormatter optionalDateTimePattern (n…...
SaaS系统如何助力企业数字化转型
随着科技的快速发展,数字化转型已经成为企业适应市场变化、提高竞争力的必要手段。在这个过程中,SaaS(软件即服务)系统以其独特的优势,正在成为越来越多企业的首选。乔拓云SaaS系统作为这一领域的佼佼者,更…...
nginx配置内网代理,前端+后端分开配置
安装好后nginx,进入配置文件 我这块安装在了home里面,各位根据自身情况选择 打开nginx.conf文件 在底部查看是否包含这段信息:含义是配置文件包含该路径下的配置文件 include /home/nginx/conf/conf.d/*.conf; # 该路径根据自己的安装位置自行修改 配置文件 进入conf.d文…...
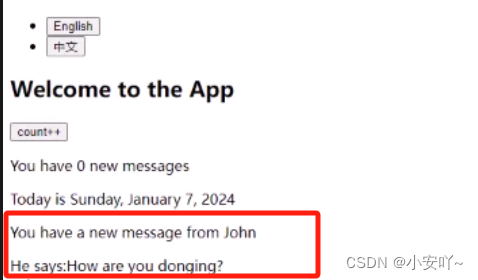
i18n多国语言Internationalization的动态实现
一、数据动态的更新 在上一篇i18n多国语言Internationalization的实现-CSDN博客,可能会遇到一个问题,我们在进行英文或中文切换时,并没有办法对当前的数据进行动态的更新。指的是什么意思呢?当前app.js当中一个组件内容ÿ…...
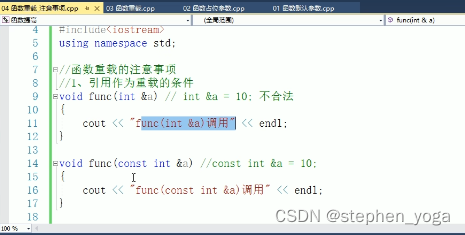
C++笔记(二)
函数的默认参数 如果我们自己传入数据,就用自己的数据,如果没有,就用默认值 语法: 返回值类型 函数名(形参默认值){} int func(int a,int b20,int c30){} …...

【技能---构建github中SSH密钥的流程】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言SSH基于账号口令的安全验证通过SSH连接到服务器打开终端(命令行界面)使用 SSH 命令连接: 在 Ubuntu 中生成 SSH 密钥并将其添…...

linux-centos服务器离线安装yapi(包含nodejs、mongodb、yapi、pm2离线安装)
yapi是使用vue框架开发的,借助nodejs 前端直接访问的mongodb数据库,离线安装yapi步骤如下 下载离线安装包 下载地址 https://download.csdn.net/download/qq445829096/88778418 离线安装包先复制到 dev/yapi目录(根据自己习惯自定义目录) node-v12.13.0-linux-x64.tar.xz …...

手撕重采样,考虑C的实现方式
一、参考文章: 重采样、上采样、下采样 - 知乎 (zhihu.com) 先直接给结论,正常重采样过程如下: 1、对于原采样率fs,需要重采样到fs1,一般fs和fs1都是整数哈,则先找fs和fs1的最小公倍数,设为m…...

网络安全产品之认识入侵防御系统
由于网络安全威胁的不断演变和增长。随着网络技术的不断发展和普及,网络攻击的种类和数量也在不断增加,给企业和个人带来了巨大的安全风险。传统的防火墙、入侵检测防护体系等安全产品在面对这些威胁时,存在一定的局限性和不足,无…...

第20课 在Android Native开发中加入新的C++类
这节课我们开始利用ffmpeg和opencv在Android环境下来实现一个rtmp播放器,与第2课在PC端实现播放器的思路类似,只不过在处理音视频显示和播放的细节略有不同。 1.压缩备份上节课工程文件夹并修改工程文件夹为demo20,将demo20导入到Eclipse或…...
)
python学习笔记11(程序跳转语句、空语句)
(一)程序跳转语句 1、break 用法:循环语句中使用,结束本层循环,一般搭配if来使用。注意while/else语法 示例: i0; while i<3:user_nameinput(请输入用户名:)pwdinput("请输入密码&a…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
