【C语言刷题系列】水仙花数的打印及进阶
1.水仙花数问题
水仙花数(Narcissistic number)也被称为超完全数字不变数(pluperfect digital invariant, PPDI)、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number)
水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身。例如:1^3 + 5^3+ 3^3 = 153。
使用C语言编程实现水仙花数的打印
首先水仙花数的范围是三位数,创建一个循环,范围是100到999
在循环内对每一个数进行判断——
- 通过取模和整除的方式将三位数的每一位都剥离出来
- 再将每一位的3次方 相加求和,与原来的三位数本身进行比较
- 如果相等,打印该数
#include<stdio.h>
int main()
{for (int i = 100; i <= 999; i++){int a = i % 10;int b = i / 10 % 10;int c = i / 100; //分别求出整数的每一位int sum = a * a * a + b * b * b + c * c * c;if (sum==i)printf("%d ", i);}printf("\n");return 0;
}
2.水仙花数问题的拓展(任意范围内整数)
对水仙花数的范围进行拓展,求出各位数字的n次方之和确好等于该数本身的数
解决思路
依然是创建一个for循环,这次的范围是10-100000(因为10以内的数对于水仙花数的要求是恒成立的,所以不在考虑范围内)
进入循环之后,因为这次不知道当下要判断的是几位数,也就不知道每一位应该计算几次方,所以要先计算出数字的位数
int count = 0;
int temp = i;//使用临时变量拷贝数字,防止原数字被破坏
while (temp)
{temp = temp / 10;//每次整除10,消除一位,直到原数字为0count++;
}接下来,就是计算每一位次方的和,这次要借助于pow库函数,所以记得添加<math.h>头文件
——pow函数用于求一个数的n次方,函数原型如下
double pow (double base, double exponent);
关于pow函数详细说明参考pow - C++ 参考 (cplusplus.com)
temp = i;//对临时变量重新赋初值(不能忘记)int sum = 0;while (temp){sum += pow(temp % 10, count);//每次求得当前最后一位数的count次方,累加到sum中temp /= 10;//求得该位之后,去除该位}
最后,得到的值存储在sum中,再来一个if语句判断
完整代码
#include<stdio.h>
#include<math.h>
int main()
{for (int i = 10; i <= 100000; i++){int count = 0; //位数计算部分int temp = i;while (temp){temp = temp / 10;count++;}temp = i; //水仙花数条件判断部分int sum = 0;while (temp){sum += pow(temp % 10, count);temp /= 10;}if (sum == i)printf("%d ", i);}return 0;
}
当然,为了封装和代码复用的考虑,可以将判断的代码放在函数内
优化后代码
#include<stdio.h>
#include<math.h> //powint get(int n)//计算位数
{int count = 0;while (n){n /= 10;count++;}return count;
}int judge(int n)//判断函数
{int temp = n;int sum = 0;while (temp){sum += pow(temp % 10, get(n));temp /= 10;}if (sum == n)return 1;elsereturn 0;
}int main()
{for (int i = 10; i <= 100000; i++){if (judge(i))printf("%d ", i);}printf("\n");return 0;
}相关文章:

【C语言刷题系列】水仙花数的打印及进阶
1.水仙花数问题 水仙花数(Narcissistic number)也被称为超完全数字不变数(pluperfect digital invariant, PPDI)、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number) 水仙花数是指一个 3 位数&a…...
ICSpector:一款功能强大的微软开源工业PLC安全取证框架
关于ICSpector ICSpector是一款功能强大的开源工业PLC安全取证框架,该工具由微软的研究人员负责开发和维护,可以帮助广大研究人员轻松分析工业PLC元数据和项目文件。 ICSpector提供了方便的方式来扫描PLC并识别ICS环境中的可疑痕迹,可以用于…...

HCIA——29HTTP、万维网、HTML、PPP、ICMP;万维网的工作过程;HTTP 的特点HTTP 的报文结构的选择、解答
学习目标: 计算机网络 1.掌握计算机网络的基本概念、基本原理和基本方法。 2.掌握计算机网络的体系结构和典型网络协议,了解典型网络设备的组成和特点,理解典型网络设备的工作原理。 3.能够运用计算机网络的基本概念、基本原理和基本方法进行…...

面试经典题---3.无重复字符的最长子串
3.无重复字符的最长子串 我的解法: 滑动窗口: 维护一个[left, right)的滑动窗口,其中[left, right - 1]都是不重复子串;每轮while循环都计算一个滑动窗口的无重复子串长度len,每轮也让right后移一步; 内部…...

使用Robot Framework实现多平台自动化测试
基于Robot Framework、Jenkins、Appium、Selenium、Requests、AutoIt等开源框架和技术,成功打造了通用自动化测试持续集成管理平台(以下简称“平台”),显著提高了测试质量和测试用例的执行效率。 01、设计目标 平台通用且支持不…...
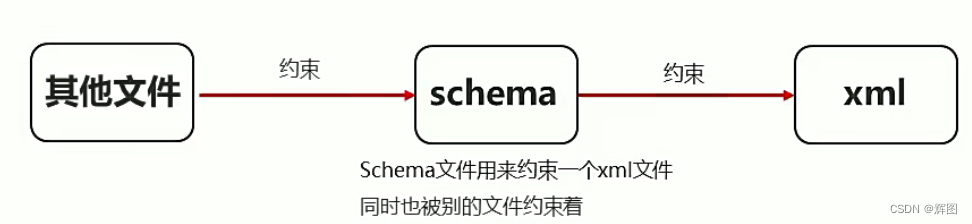
Java基础进阶02-xml
目录 一、XML(可拓展标记语言) 1.学习网站: 2.作用 3.XML标签 4.XML语法 5.解析XML (1)常见解析思想DOM 6.常见的解析工具 7.DOM4j的使用 8.文档约束 (1)概述 (2…...

《开始使用PyQT》 第01章 PyQT入门 03 用户界面介绍
03 用户界面介绍 《开始使用PyQT》 第01章 PyQT入门 03 用户界面介绍 The user interface (UI) has become a key part of our everyday lives, becoming the intermediary between us and our ever-growing number of machines. A UI is designed to facilitate in human-co…...

HTML-列表
列表 abbr: li : list item ol : orderd list ul : unordered list dl : definition list dt : definition title dd : definition description 1.有序列表(order list) 概念:有顺序或侧重顺序的列表 <h2>要把大象放冰箱总共分几步</h2> &…...
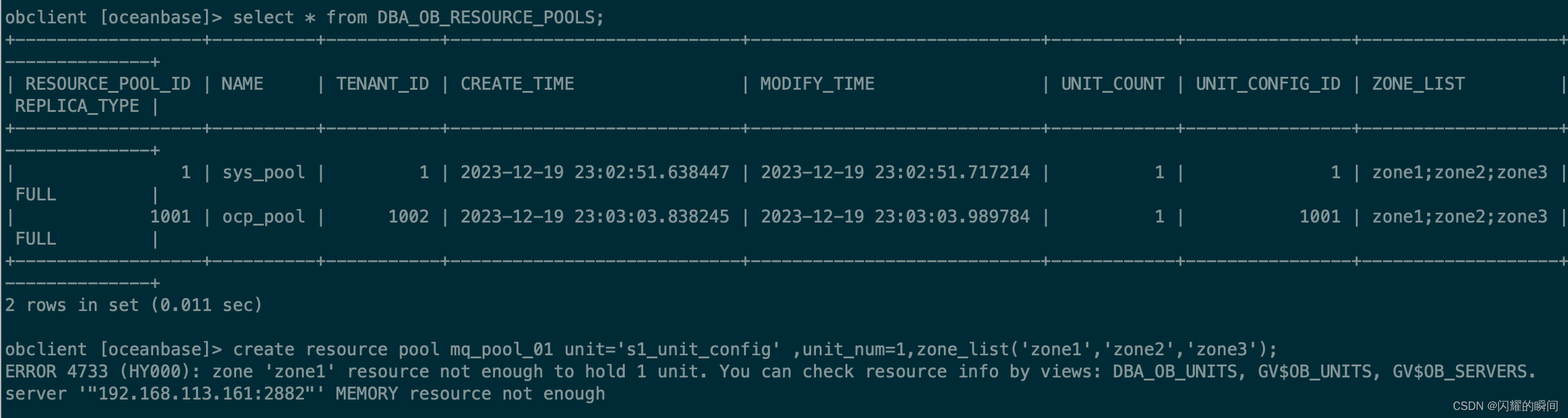
OceanBase创建租户
租户是集群之上的递进概念,OceanBase 数据库采用了多租户架构。 集群偏部署层面的物理概念,是 Zone 和节点的集合,租户则偏向于资源层面的逻辑概念,是在物理节点上划分的资源单元,可以指定其资源规格,包括…...
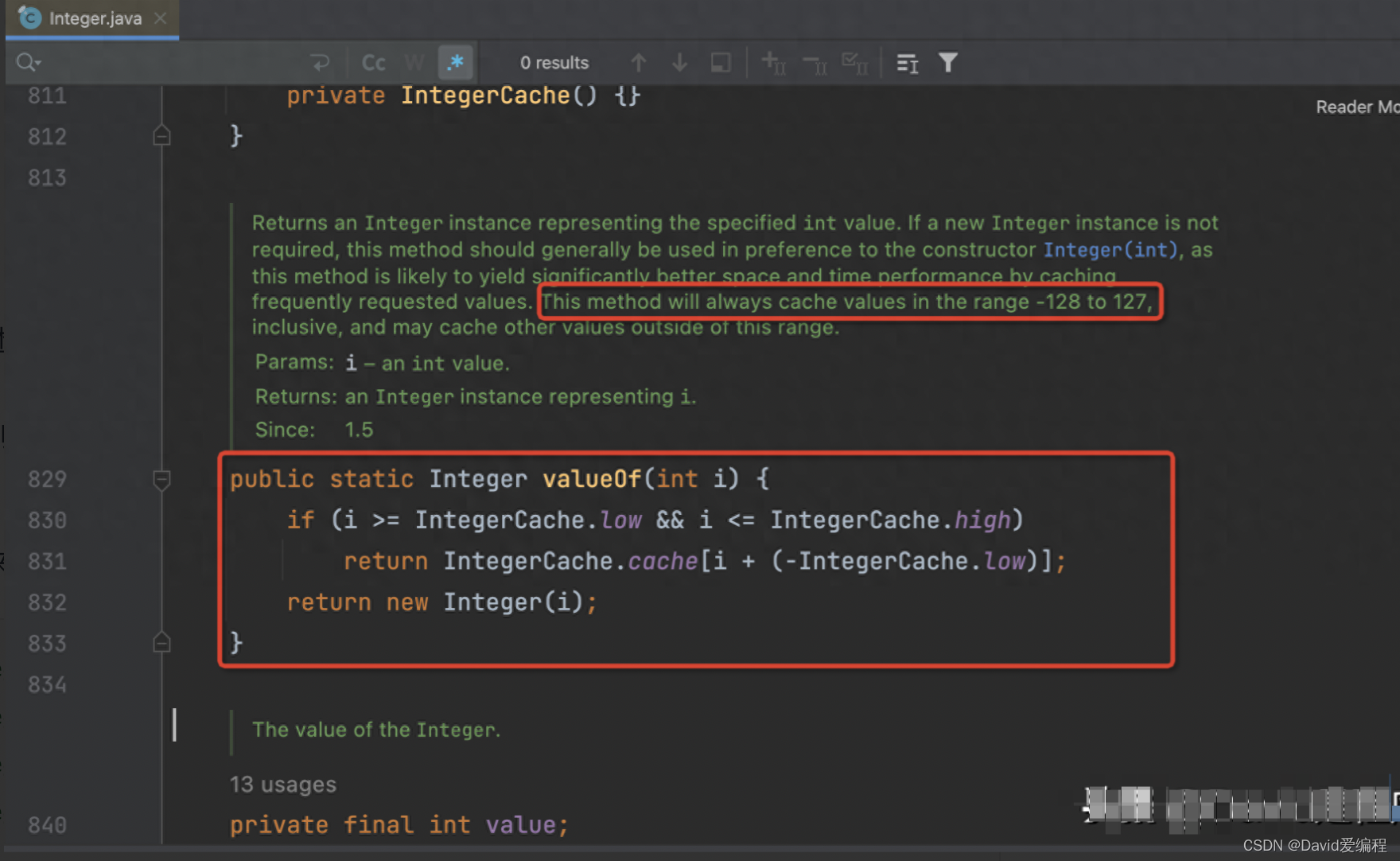
Java中Integer(127)==Integer(127)为True,Integer(128)==Integer(128)却为False,这是为什么?
文章目录 1.前言2. 源码解析3.总结 1.前言 相信大家职业生涯中或多或少的碰到过Java比较变态的笔试题,下面这道题目大家应该不陌生: Integer i 127; Integer j 127;Integer m 128; Integer n 128;System.out.println(i j); // 输出为 true System.o…...
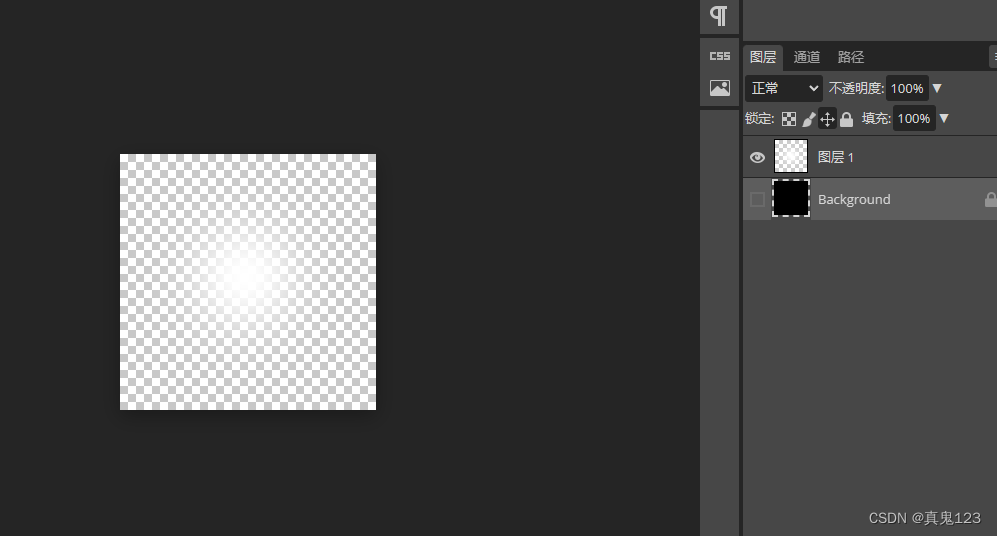
【Unity】粒子贴图异常白边问题
从PS制作的黑底,白光的贴图。放入Unity粒子中,拉远看会有很严重的白边,像马赛克一样。 材质使用:Mobile/Particles/Additive 经测试只使用一张黑色的图片,也会有白边。 解决方案: 关闭黑色底…...

bxCAN接收处理
接收处理 为了接收 CAN 消息,提供了构成 FIFO(First Input First Output) 的三个邮箱。为了节约 CPU 负载,简化软件并保证数据一致性,FIFO 完全由硬件进行管理。应用程序通过 FIFO 输出邮箱访问 FIFO 中所存储的消息。 有效消息 当消息依据…...
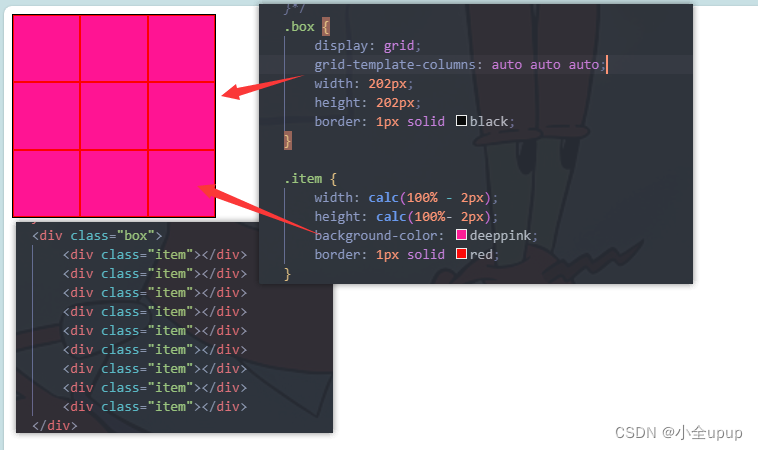
前端面试题-(浏览器内核,CSS选择器优先级,盒子模型,CSS硬件加速,CSS扩展)
前端面试题-(浏览器内核,CSS选择器优先级,盒子模型,CSS硬件加速,CSS扩展) 常见的浏览器内核CSS选择器优先级盒子模型CSS硬件加速CSS扩展 常见的浏览器内核 内核描述Trident(IE内核)主要用在window系统中的IE浏览器中&…...

WEB前端标签的使用
图片标签 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><body><!-- img标签就是用来将图片显示在页面上的标签 --><img src"图片路径"><!-- 可用路径&#…...

739. 每日温度
提示给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1: 输入: tempe…...
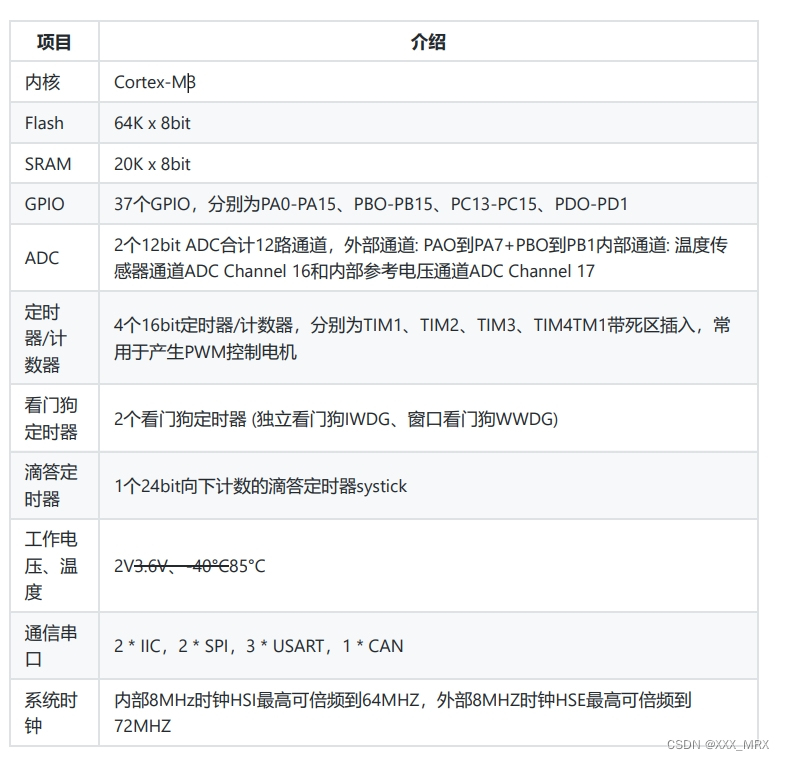
stm32F103C8T6简介及标准库和HAL库的区别
什么是单片机 单片机是一种集成电路芯片,把具有数据处理能力的中央处理器CPU、随机存储器RAM、只读存储器ROM、多种I/O和中断系统、定时器/计数器等功能(可能还包括显示驱动电路、脉宽调制电路、模拟多路转换电路、A\D转换器等电路)集成到一…...

操作系统(3)---操作系统引导
在安装操作系统后,磁盘的分布如下: C盘是这个磁盘的活动分区(又称主分区),安装了操作系统 开机过程如下: 1.计算机的主存由RAM和ROM组成,RAM关机数据消失,而ROM(Basic In…...

Vue3+Ts:实现paypal按钮
Vue3Ts:实现paypal按钮 一、前端页面按钮实现第一步:下载paypal.js依赖第二步:引入要使用的vue页面,并调用。 二、实现逻辑研究第一点:了解下Buttons自带的style属性第二点:了解下Buttons自带的处理方法第三…...

.[Decipher@mailfence.com].faust 勒索病毒数据怎么处理|数据解密恢复
尊敬的读者: 随着网络技术的发展,勒索病毒已经成为数字时代中一种极具破坏性的威胁。[support2022cock.li].faust [tsai.shenmailfence.com].faust [Encrypteddmailfence.com].faust[Deciphermailfence.com].faust 勒索病毒是其中的一种,它以…...
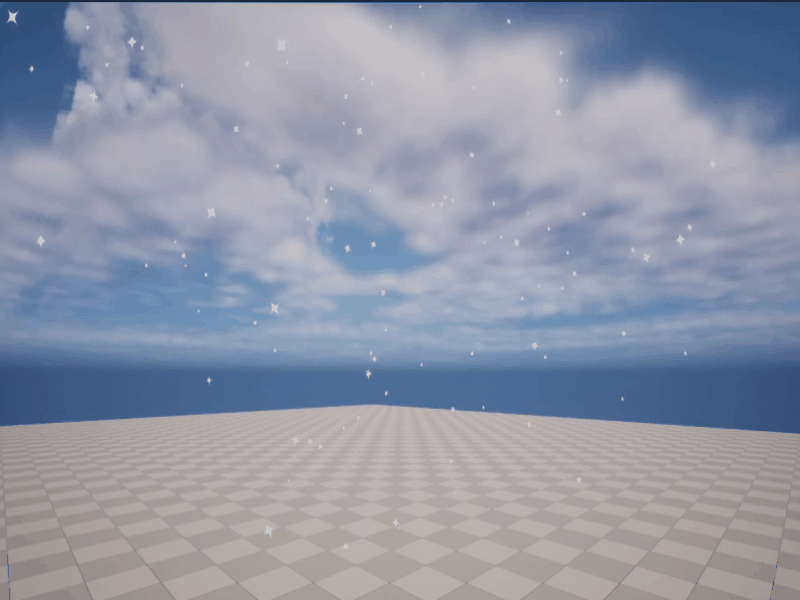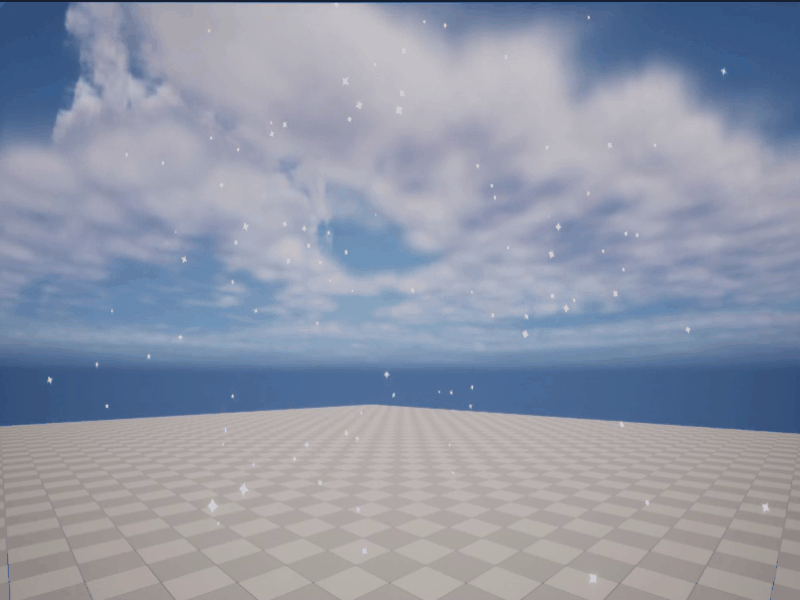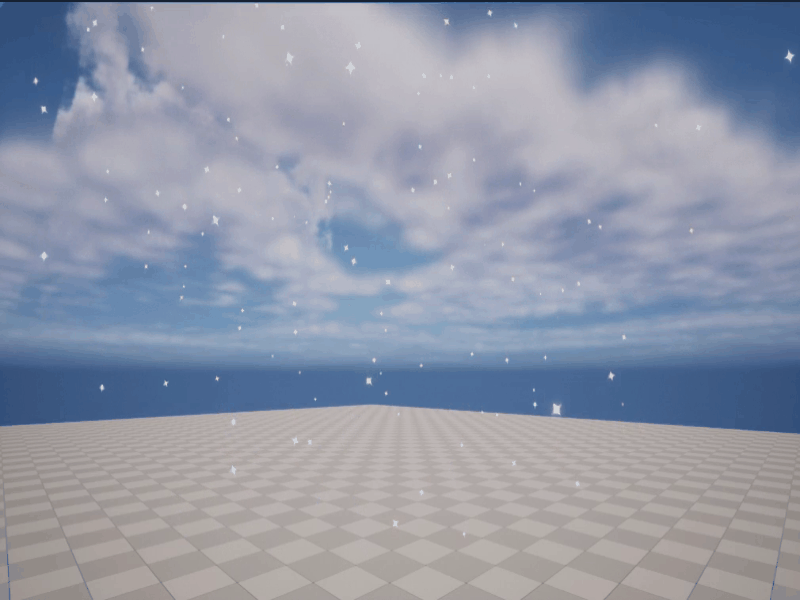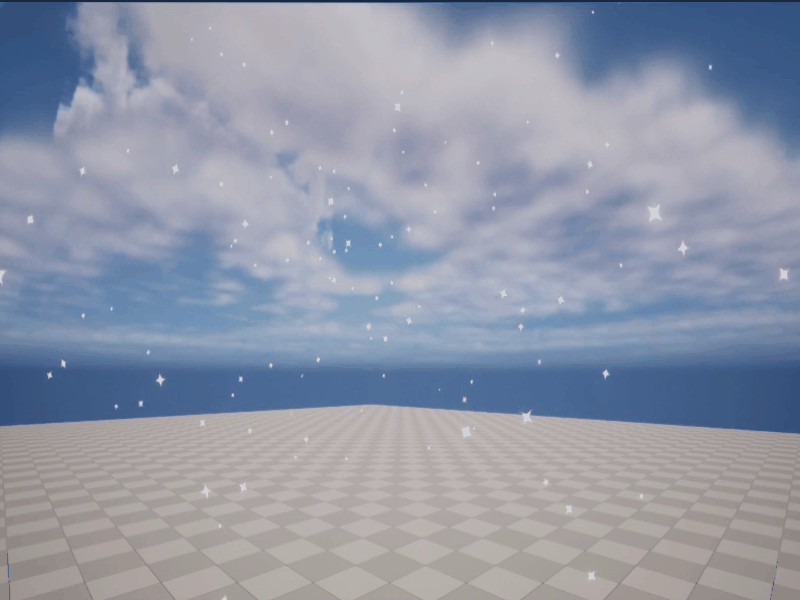
【UE Niagara】制作星光飘落效果
效果 步骤 1. 新建一个Niagara系统 选择模板“Fountain” 这里命名为“NS_Flare” 打开“NS_Flare”,选中Sprite渲染器,设置材质为上一篇文章中(【UE 材质】闪烁的星星材质)制作的材质“M_Flare” 2. 由于要在Niagara中调整粒子的…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
