Java -数据结构，【优先级队列 / 堆】

一、二叉树的顺序存储

在前面我们已经讲了二叉树的链式存储，就是一棵树的左孩子和右孩子
而现在讲的是：顺序存储一棵二叉树。

1.1、存储方式

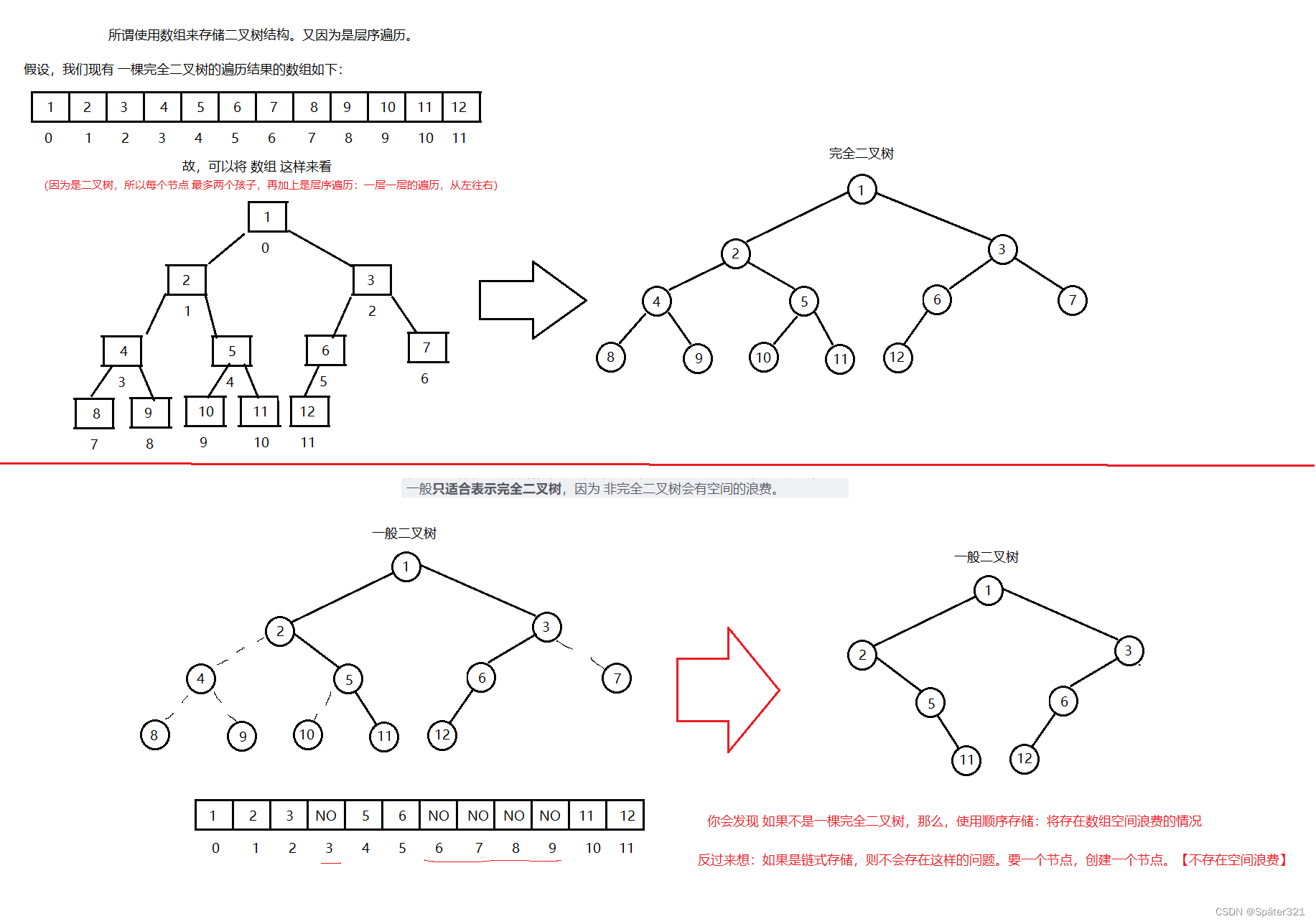
使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。 一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。
这种方式的主要用法就是堆的表示

下标关系

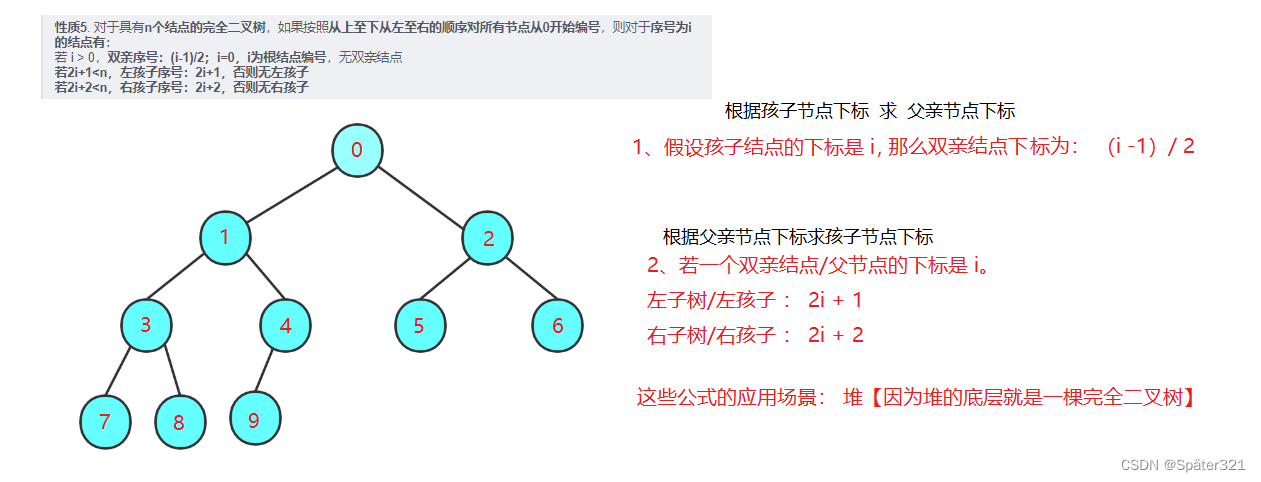
已知双亲(parent)的下标，则：
左孩子(left)下标 = 2 * parent + 1;
右孩子(right)下标 = 2 * parent + 2;

已知孩子（不区分左右）(child)下标，则：
双亲(parent)下标 = (child - 1) / 2;

也就是前面我们将的性质5：
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的结点有：

（1）若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
（2）若2i+1<n，左孩子序号：2i+1，否则无左孩子
（3）若2i+2<n，右孩子序号：2i+2，否则无右孩子

二、堆

2.1、概念

1. 堆逻辑上是一棵完全二叉树
2. 堆物理上是保存在数组中
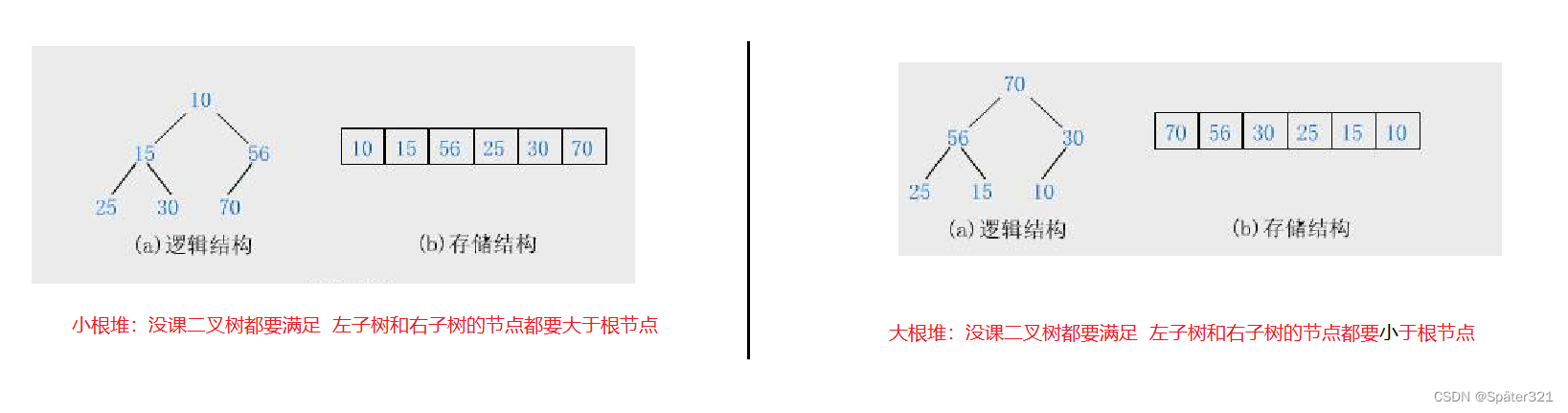
3. 满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆
4. 反之，则是小堆，或者小根堆，或者最小堆
5. 堆的基本作用是，快速找集合中的最值 ：无论是 大根堆还是小根堆， 它们的 最值【最大值 和 最小值】都处于 二叉树的 根结点处。要想获得 最值，直接 peek 方法，就能获得 树 的 根结点值 / 最值。
   

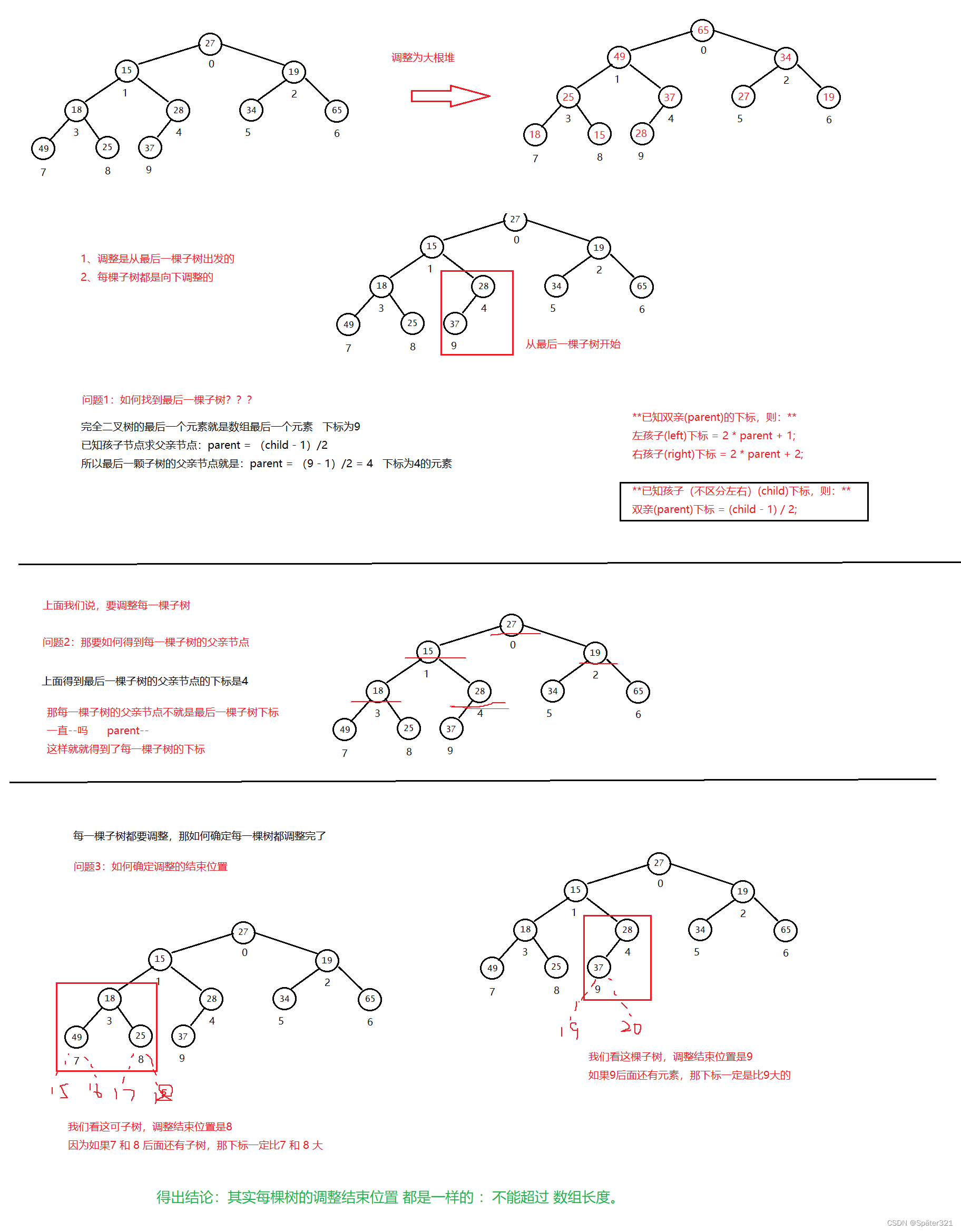
2.2、操作-向下调整

前提：左右子树必须已经是一个 堆 / 逻辑上是一棵完全二叉树。
将一组 记录完全二叉树数据 的 数组 转换成 大根堆。

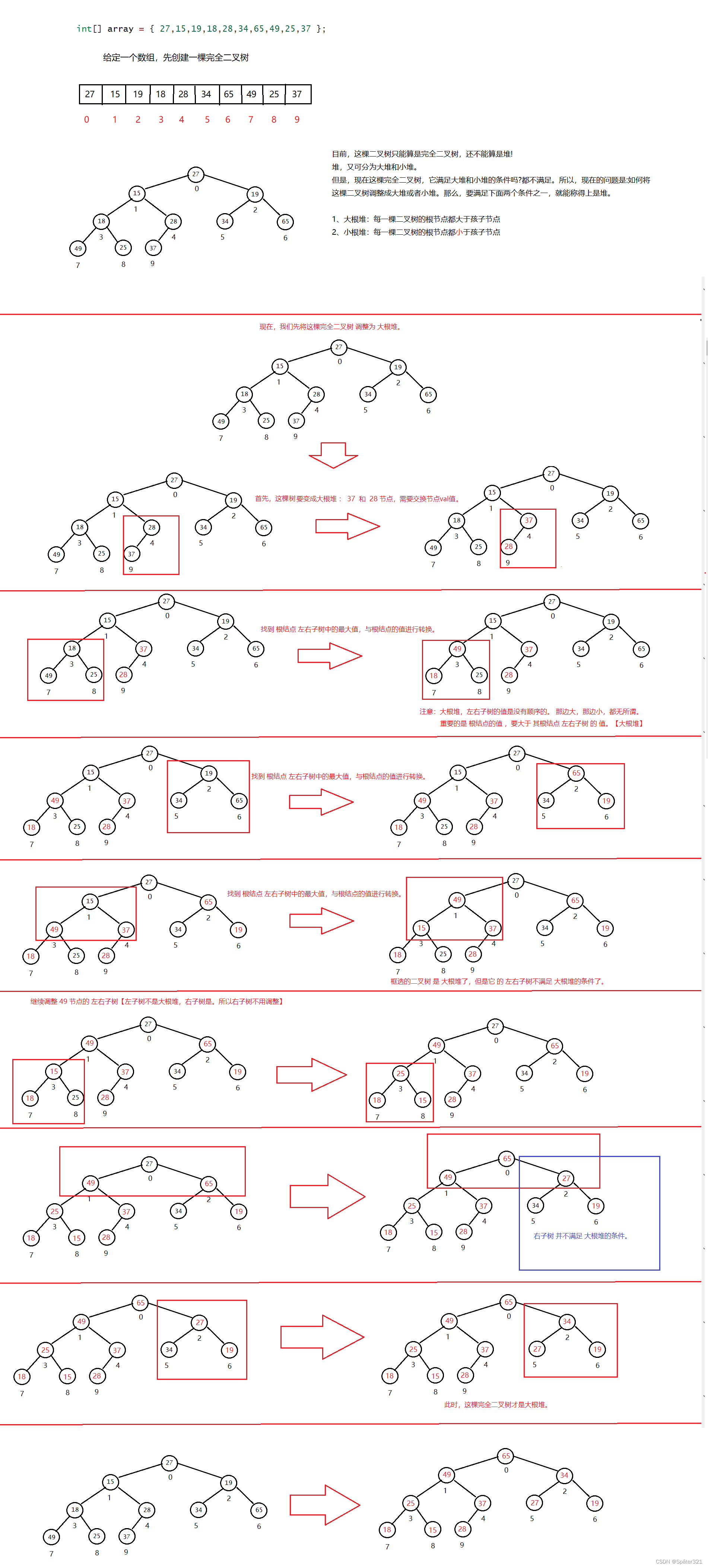
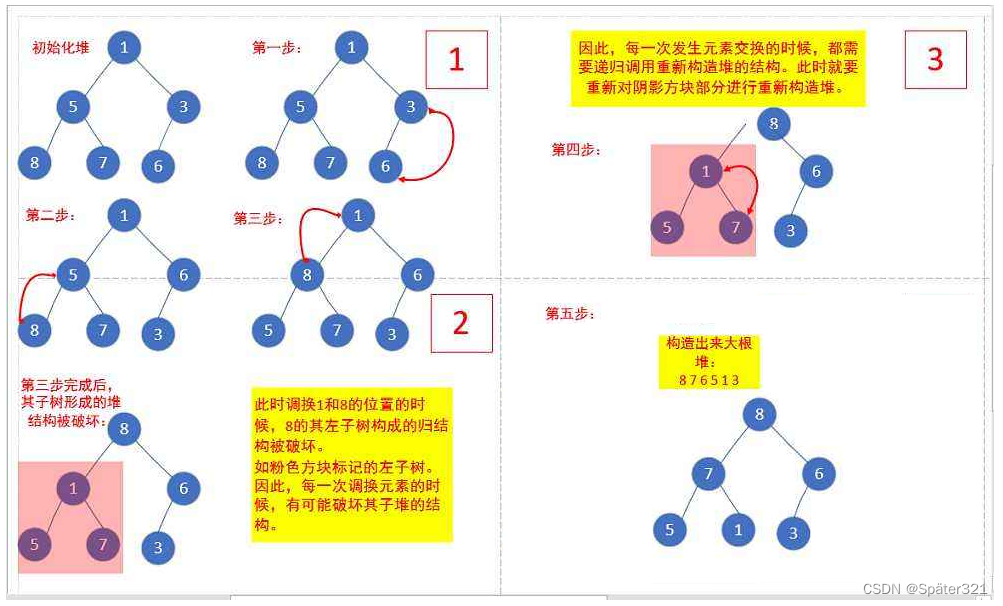
向下调整出现的问题：

得出结论:其实每棵树的调整结束位置都是一样的︰不能超过数组长度。

如何构造一个 向下调整的函数 - 重点

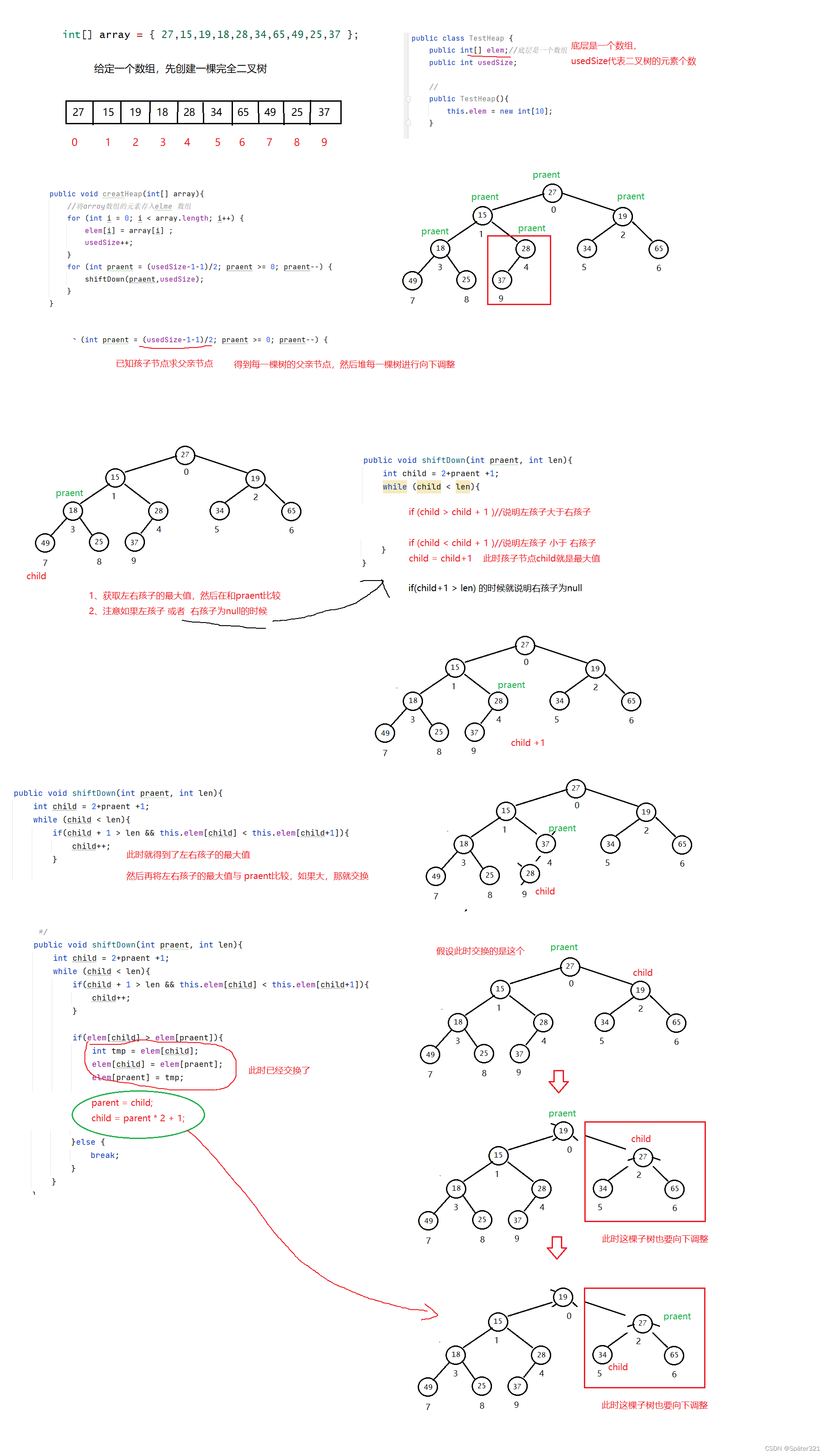
public class TestHeap {public int[] elem;//底层是一个数组public int usedSize;//public TestHeap(){this.elem = new int[10];}/*** 创建堆* @param array 堆里面存放的元素*/public void creatHeap(int[] array){//将array数组的元素存入elme 数组for (int i = 0; i < array.length; i++) {elem[i] = array[i] ;usedSize++;}for (int praent = (usedSize-1-1)/2; praent >= 0; praent--) {shiftDown(praent,usedSize);}}/*** 向下调整* @param praent 每棵子树的父亲节点* @param len 调整的结束位置，不能大于数组的长度*/public void shiftDown(int praent, int len){int child = 2+praent +1;while (child < len){if(child + 1 > len && this.elem[child] < this.elem[child+1]){child++;}if(elem[child] > elem[praent]){int tmp = elem[child];elem[child] = elem[praent];elem[praent] = tmp;}else {break;}}}
}

测试一下：

模拟实现 堆 的 时间复杂度

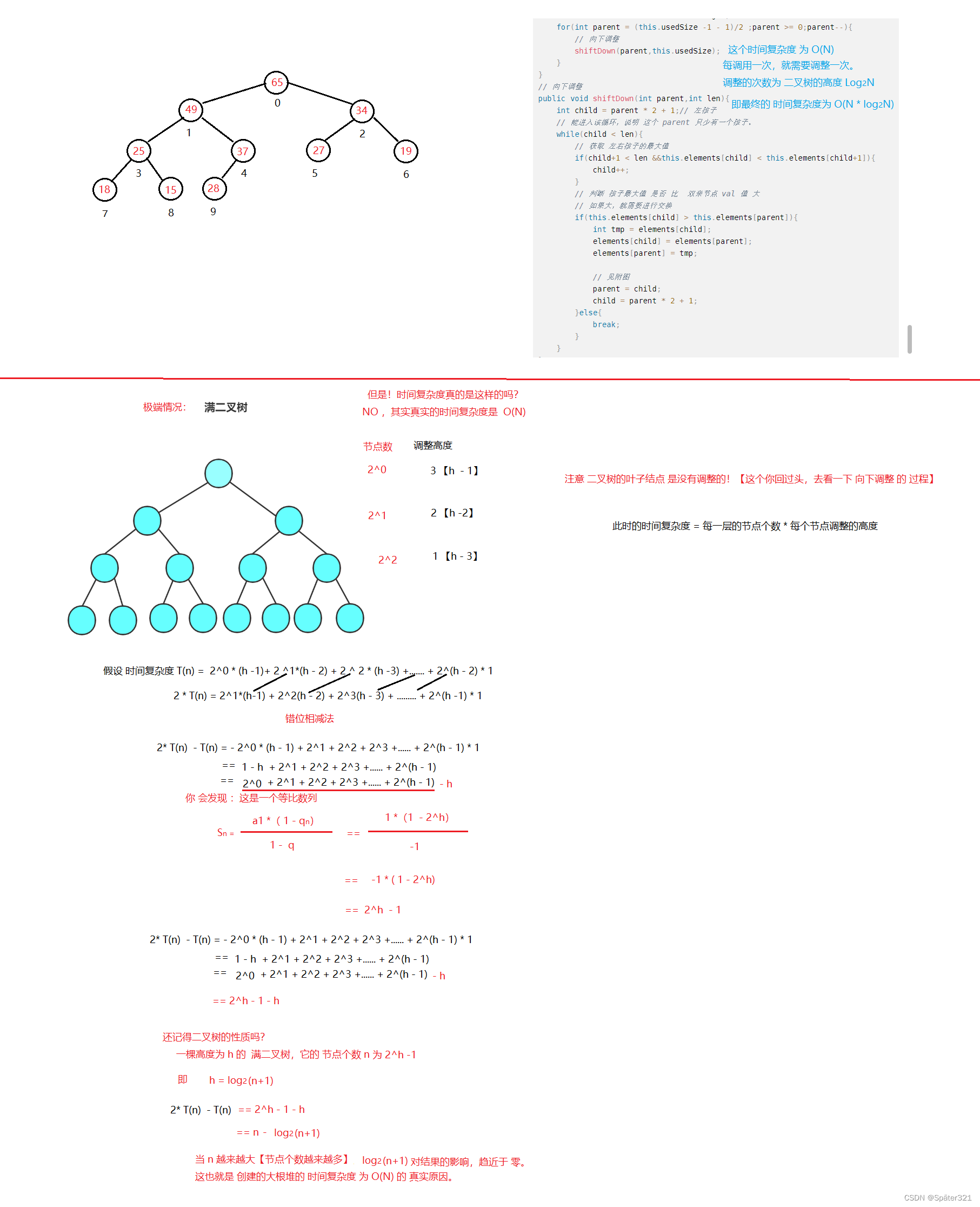
上图转载于：堆 / 优先队列

粗略估算，可以认为是在循环中执行向下调整，为 O(n * log(n))
（了解）实际上是 O(n)
堆排序中建堆过程时间复杂度O(n)怎么来的？

2.3、操作-建堆

下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的子树开始调整，一直调整到根节点的树，就可以调整成堆

图示（以大堆为例）：

// 建堆前
int[] array = { 1,5,3,8,7,6 };
// 建堆后
int[] array = { 8,7,6,5,1,3 };

三、堆的应用-优先级队列

3.1、概念

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次
高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。
在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这
种数据结构就是优先级队列(Priority Queue)

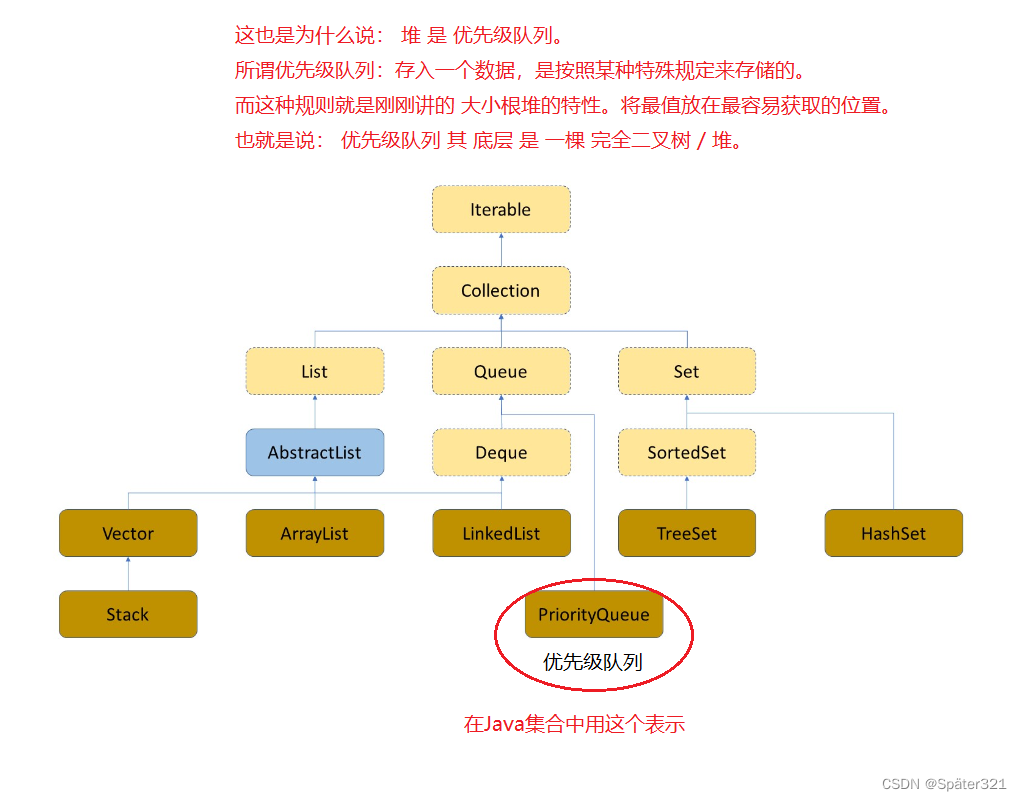
优先级队列的实现方式有很多，但最常见的是使用堆来构建

3.2、堆的基本操作

我们知道堆分为大根堆和小根堆，那Java中自带的默认是大根堆还是小根堆？？？
Java集合中默认是小根堆

我们测试一下：

public static void main(String[] args) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();priorityQueue.offer(12);priorityQueue.offer(3);priorityQueue.offer(18);System.out.println(priorityQueue.poll());System.out.println(priorityQueue.poll());}

优先级队列 - 模拟实现入队 – offer（）

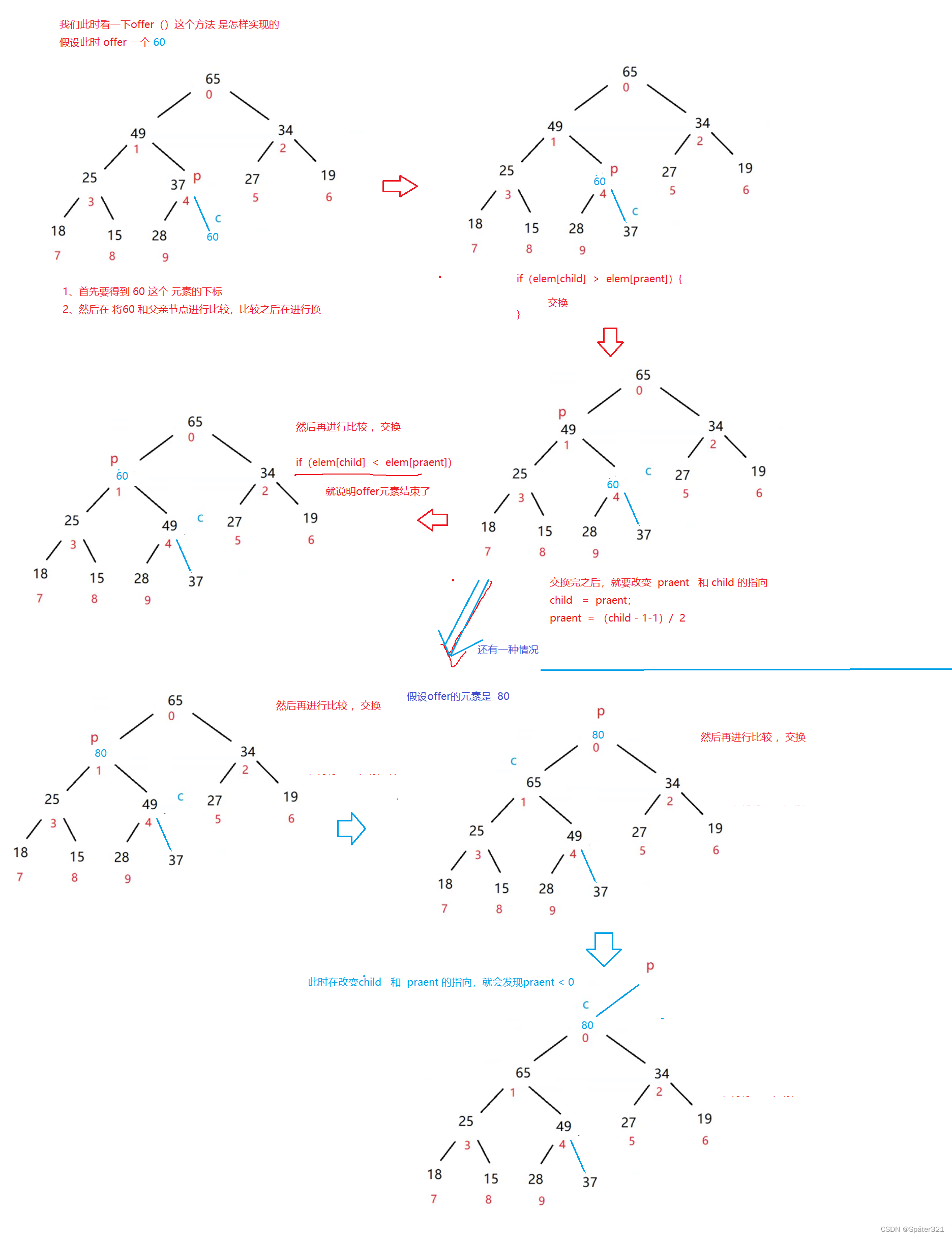
/***  插入元素* @param val*/public void offer(int val){if(isFull()){//扩容elem = Arrays.copyOf(elem,2*elem.length);}//没有满就将val放在数组的最后一个元素elem[usedSize] = val;usedSize++;//然后就调整堆，使其成为一个大根堆shiftUp(usedSize-1,val);}/**** @param child 孩子节点的坐标* @param val 要插入的值*/public void shiftUp(int child, int val){int praent = (child - 1) / 2;while(praent > 0){if(elem[child] > elem[praent]){int tmp = elem[child];elem[child] = elem[praent];elem[praent] = tmp;//然后再改变child 和 praent 的指向child = praent;praent = (child - 1) / 2;}else {break;}}}public boolean isFull(){return this.elem.length == usedSize;}

优先级队列 - 模拟实现出队 – poll（）

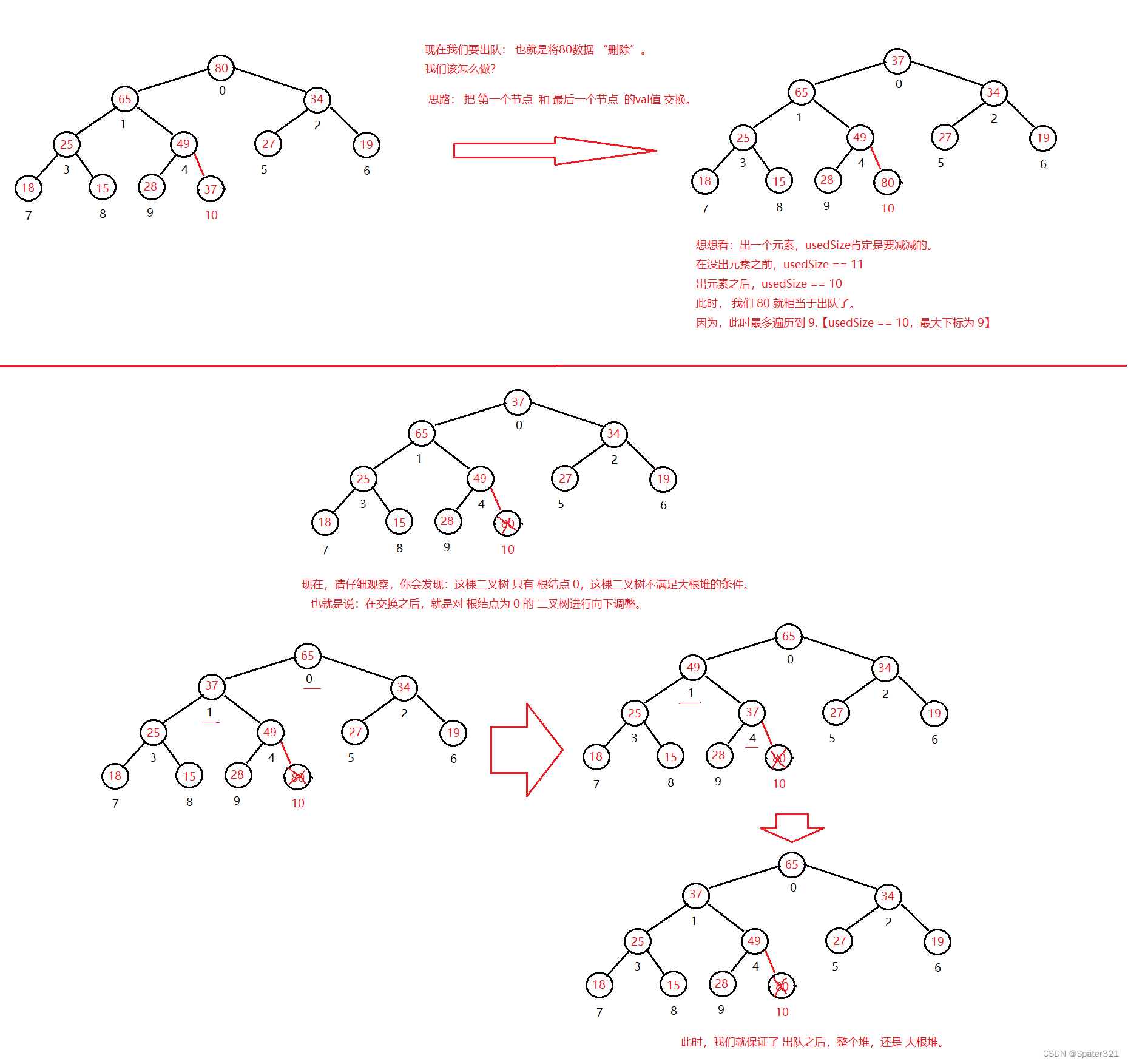
public int poll(){if(isFull()){throw new RuntimeException("队列为null！");}//先将0下标和数组的最后一个元素交换int tmp = elem[0];elem[0] = elem[usedSize-1];elem[usedSize-1] = tmp;usedSize--;//然后向下调整0下标这棵树shiftDown(0,usedSize);return tmp;}//判断是否为nullpublic boolean isEmpty(){if (usedSize == 0){return true;}return false;}

总程序

public class Heap {public int[] elements;// 底层数组public int usedSize;// 有效元素个数// 构造方法public Heap(){// 数组初始化容量this.elements = new int[10];}// 创建堆，获取 输入数组 的 数据public void creationHeap(int[] array){this.usedSize += array.length;if(isFull()){this.elements = Arrays.copyOf(this.elements,this.elements.length*2);}this.elements = Arrays.copyOf(array,array.length);for(int parent = (this.usedSize -1 - 1)/2 ;parent >= 0;parent--){// 向下调整shiftDown(parent,this.usedSize);}}// 向下调整public void shiftDown(int parent,int len){int child = parent * 2 + 1;// 左孩子// 能进入该循环，说明 这个 parent 只少有一个孩子。while(child < len){// 获取 左右孩子的最大值if(child+1 < len &&this.elements[child] < this.elements[child+1]){child++;}// 判断 孩子最大值 是否 比  双亲节点 val 值 大// 如果大，就需要进行交换if(this.elements[child] > this.elements[parent]){int tmp = elements[child];elements[child] = elements[parent];elements[parent] = tmp;// 见附图parent = child;child = parent * 2 + 1;}else{break;}}}// 入队操作public void offer(int val){if(isFull()){// 扩容this.elements = Arrays.copyOf(this.elements,this.elements.length * 2);}elements[usedSize++] = val;//usedSize++;shiftUp(usedSize-1);// 有效元素个数 是 usedSize,最后一个元素的下标是 usedSize -1}private void shiftUp(int child){int parent = (child - 1)/2;while(child > 0){if(this.elements[child] > this.elements[parent]){int tmp = this.elements[child];this.elements[child] = this.elements[parent];this.elements[parent] = tmp;child = parent;parent = (child - 1) / 2;}else{break;}}}// 判断队列满没满public boolean isFull(){return this.usedSize >= this.elements.length;}// 出队操作public int poll(){if(isEmpty()){throw new RuntimeException("优先级队列为空！");}int tmp = this.elements[0];this.elements[0] = this.elements[this.usedSize -1];this.elements[this.usedSize - 1] = tmp;this.usedSize--;shiftDown(0,usedSize);return tmp;}// 判断队列 空不空public boolean isEmpty(){return this.usedSize == 0;}public int peek(){if(isEmpty()){throw new RuntimeException("优先级队列为空！");}return this.elements[0];}}

四、校招 – TopK问题

问题描述：

从arr[1, n]这n个数中，找出最大的k个数，这就是经典的TopK问题。（从100万中找出最大的k个数）

栗子：

从arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 这n=12个数中，找出最大的k=5个。

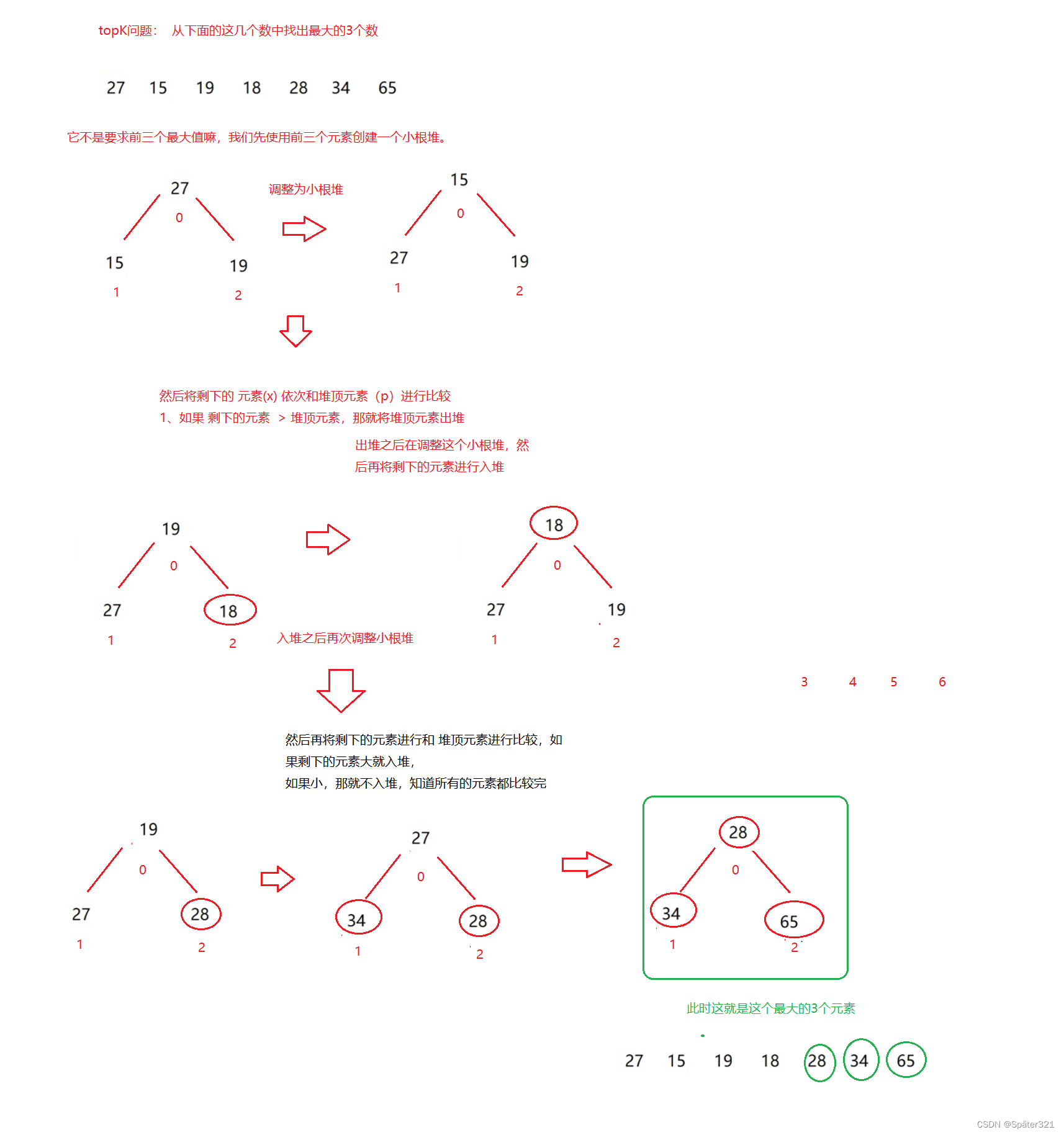
总结

1、如果求前K个最大的元素，要建一个小根堆。
2、如果求 前K个最小的元素，要建一个大根堆。
3、如果是求第k大的元素，建一个小堆，小根堆 堆顶的元素就是第k大的元素。
4、如果是求第k小的元素，建一个大堆，大根堆 堆顶的元素就是第k小的元素。

五、堆的其他应用-堆排序

1、将数据调整为 大根堆、
2、0 下标 与 最后一个未排序的元素进行交换即可。
3、循环上述两个操作，直至 最后一个未排序的元素 下标为 0.。

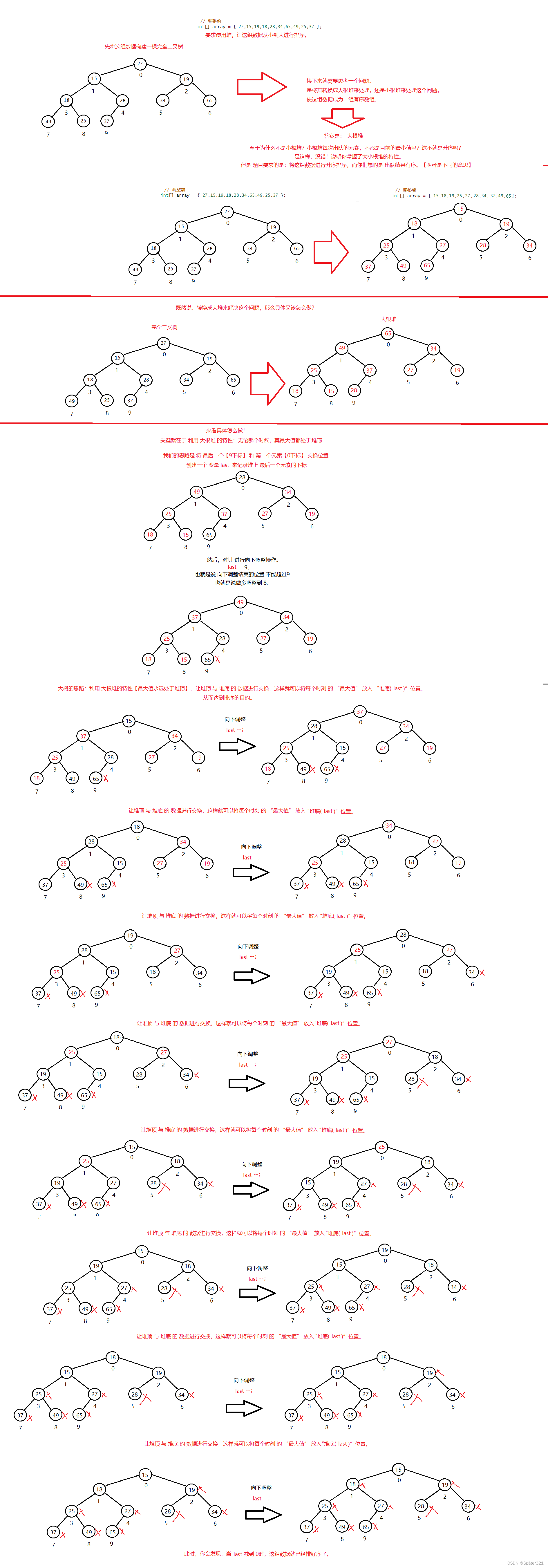
/*** 堆排序*/public void heapSort(){int last  = usedSize - 1;while (last  > 0){int tmp = elem[0];elem[0] = elem[last ];elem[last ] = tmp;shiftDown1(0,last);last --;}}/***向下调整* @param parent* @param len*/public void shiftDown1(int parent,int len){int child = parent * 2 + 1;// 左孩子// 能进入该循环，说明 这个 parent 只少有一个孩子。while(child < len){// 获取 左右孩子的最大值if(child+1 < len &&this.elem[child] < this.elem[child+1]){child++;}// 判断 孩子最大值 是否 比  双亲节点 val 值 大// 如果大，就需要进行交换if(this.elem[child] > this.elem[parent]){int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;parent = child;child = parent * 2 + 1;}else{break;}}}