Java七大排序详解
排序
排序的概念
所谓排序 ,就是让一串记录,按照其中某些或者某个关键字的大小,递增或递减的排列起来的操作。
稳定性:就比如在待排序的序列中,存在多个具有相同关键字的记录 ,如果经过排序这些相同的关键字相对位置还是不变,则称这种排序是稳定的;否则就是不稳定的。下面用图例来解析一下:
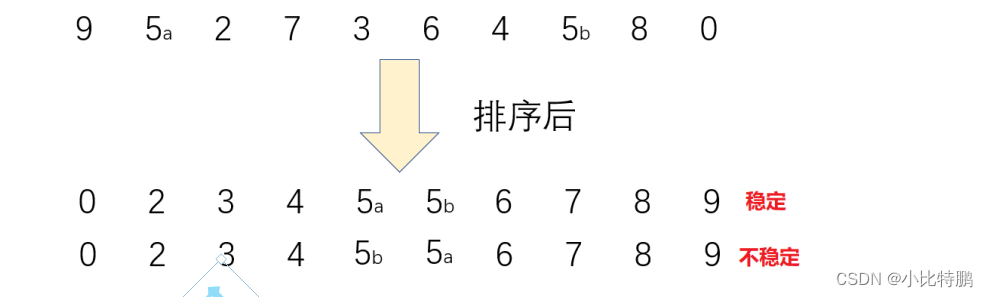
排序还分为内部排序和外部排序:
内部排序: 数据元素全部在内存中排序。
外部排序: 数据元素大多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
插入排序
插入排序
直接插入排序就是一种简单的插入排序法:他就是把待排序的记录按照其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为一个新的有序序列。在实际生活中 我们玩扑克牌时,就应用了插入排序的思想。
步骤:
从第2个元素开始如果第一个元素比第二个元素大 那就得交换 一直往前遍历直到小于0下标 在待排序元素中,假设前n-个元素已经有序 如果第n个元素比第n-1个元素大 那说明前n个已经有序 ,如果比他小就按照遍历一直找到比前面的数字大为止 找到就插入进去就行。
因为我们不能够确定待排序中哪一部分是有序的 ,所以我们从第二个元素开始遍历 默认第一个元素是有序的 ,再依次遍历后面的元素 再慢慢插入进来 ,变成一个新的有序序列。
下面让我们用动图演示一遍:

代码实现如下:
//插入排序public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {//要定义一个变量存一下i下标的值int tmp = array[i];int j = i - 1;for (; j >= 0; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}
时间复杂度:最好情况下(待排序列是升序的)为O(N);最坏情况下(待排序列是逆序的)为O(N2),
空间复杂度:O(1);而且插入排序是稳定的
希尔排序
希尔排序
希尔排序又称为缩小增量法。希尔排序法的基本思想是:先给定一个整数gap,把待排序文件中所有的记录分为多个组,所有距离为gap的记录分为一组,并对每一组的记录进行排序 然后重复上诉操作直到gap= 1时 所有记录都排好序了
动图表示如下:

代码如下:
//希尔排序public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {gap = gap / 2; //或者可以写成 gap = gap / 3 + 1shell(array, gap);}}private static void shell(int[] array, int gap) {//每组的数据都在变化for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (array[j] > tmp) {array[j + gap] = array[j];} else {break;}array[j + gap] = tmp;}}}时间复杂度:希尔排序的时间复杂度 是不好计算的 他会根据gap的取值的不同而不同。通过大量的实验,现在时间复杂度只能在O(n1.25) ~O(1.6*n1.25)来计算。
空间复杂度:O(1);
希尔排序是快速排序的优化 ,希尔排序是不稳定的。
选择排序
选择排序
选择排序的思想就是 每次遍历待待排序中的元素 选出最小值,排到序列的起始位置 ,一直排 直到全部排完 比如说现在第一个元素是4 后面找完待排序如果有比4小的就换 没有就不换。
动图演示:

代码表示如下:
//选择排序public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {//定义一个临时变量把i下标存下来int minIndex = i;int j = i + 1;for (; j < array.length; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array, minIndex, i);}}
时间复杂度:最坏情况:O(N2),最好情况:O(N2);
空间复杂度:O(1)
选择排序不稳定
冒泡排序
冒泡排序
冒泡排序的思想 :就是遍历和交换 如果左边的大于右边就交换 排下来 最大的就在右边了 。
具体情况看动图演示:

代码实现如下:
// 冒泡排序public static void bubbleSort(int[] array) {// write code herefor (int i = 0;i<array.length;i++){for (int j =0;j < array.length-1-i;j++){if (array[j]<array[j+1]){swap(array,j,j+1);}}}}
时间复杂度:最坏情况下:O(N2),最好情况下:O(N)
空间复杂度:O(1)
快速排序法
快速排序算法
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任意取待排序元素序列中的某元素作为基准值,按照该排序码将排序集合分割为两个子序列,让左子序列中所有元素均小于基准值,右子序列均大于基准值,然后递归左和右 直到所有元素有序。
快排右可以分为两种方法去实现 Hoare法 和 挖坑法。
Hoare法
用最左边的值作为一个tmp,定义一个left和right,left从左往右走 ,right从右往左走 ,一定要right先走,这样才能保证相遇时候的值是小于tmp的值。 在走的过程中,如果right遇到比tmp小的值,就停下来等left走直到left遇到一个比tmp大的数 left和right的值交换 right继续走 直到他们相遇,将相遇的值和tmp交换。此时tmp的左边都是小于tmp的数 ,右边都是大于tmp的数。
动图演示:

代码表示如下:
//快速排序public static void quickSort(int[] array) {quick(array,0,array.length-1);//取闭区间}private static void quick(int[] array,int start,int end) {if (start >= end){return;}int pivot = partitionHoare(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}//Hoare法private static int partitionHoare(int[] array,int left,int right) {int tmp = array[left];//基准int i =left;while (left < right) {while (left < right && array[right] >= tmp) {right--;}while (left < right && array[left] <= tmp) {left++;}swap(array,left,right);}//相遇了 换swap(array,i,left);return left;}
挖坑法
挖坑法的思路和Hoare法差不多
就是选最左边或者最右边的数据作为一个坑,也是定义两个指针在两边走
我们直接看动图演示:

代码实现如下:
//快速排序public static void quickSort(int[] array) {quick(array,0,array.length-1);//取闭区间}private static void quick(int[] array,int start,int end) {if (start >= end){return;}int pivot = partition(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}
//挖坑法private static int partition(int[] array,int left,int right) {int tmp = array[left];while (left < right){while (left < right && array[right] >= tmp) {right--;}if (left >= right){break;}array[left] = array[right];while (left < right && array[left] <= tmp) {left++;}if (left >= right){break;}array[right] = array[left];}array[left] = tmp;return left;}
还有非递归写法:
//快速排序非递归实现public static void quickSortNor(int[] array) {Stack<Integer> stack = new Stack<>();int left = 0;int right = array.length-1;int pivot = partition(array,left,right);if(pivot-1 > left) {stack.push(left);stack.push(pivot-1);}if(pivot + 1 < right) {stack.push(pivot+1);stack.push(right);}while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();pivot = partition(array,left,right);if(pivot-1 > left) {stack.push(left);stack.push(pivot-1);}if(pivot + 1 < right) {stack.push(pivot+1);stack.push(right);}}}
归并排序
归并排序
归并排序和快速排序一样采用了分治的思想,他就是将待排序的数组不断拆分,直到拆到区间里只有一个元素为止,然后开始合并 一层一层地合并 直到整个数组有序。这里很显然要用递归的方式去实现归并排序。 归并排序就是典型用空间换时间的一种排序。
动图演示:

代码实现:
//归并排序public static void mergeSort(int[] array) {mergeFunc(array,0,array.length-1);}private static void mergeFunc(int[] array,int left,int right) {if (left >= right) {return;}int mid = left +((right - left) >> 1);mergeFunc(array,left,mid);mergeFunc(array,mid+1,right);//左边分解完 ,右边分解完 开始合并merge(array,left,mid,right);}private static void merge(int[] array,int left,int mid,int right) {int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;int[] tmpArray = new int[right-left+1];int k = 0;//得保证两个表都有数据while (s1 <= e1 && s2 <= e2) {if (array[s1] <= array[s2]) {tmpArray[k++] = array[s1++];}else {tmpArray[k++] = array[s2++];}}//2.看还有哪个数组还有数据 直接加在数组后面while (s1 <= e1) {tmpArray[k++] = array[s1++];}while (s2 <= e2) {tmpArray[k++] = array[s2++];}//拷贝到原来的数组for (int i = 0;i < k;i++) {array[i+left] = tmpArray[i];}}
时间复杂度:O(Nlog2N)
空间复杂度:O(N)
归并排序稳定
堆排序
排序的思想:首先得将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是**堆结构的顶端。**然后将顶端的数将最后一个元素交换,此时末尾为最大值,待排序元素就剩n-1个了。然后再将剩下的n-1个元素调整为大根堆,循环去执行此操作最后便可以得到有序的数组。
升序用大根堆 ,降序用小根堆。
图解:
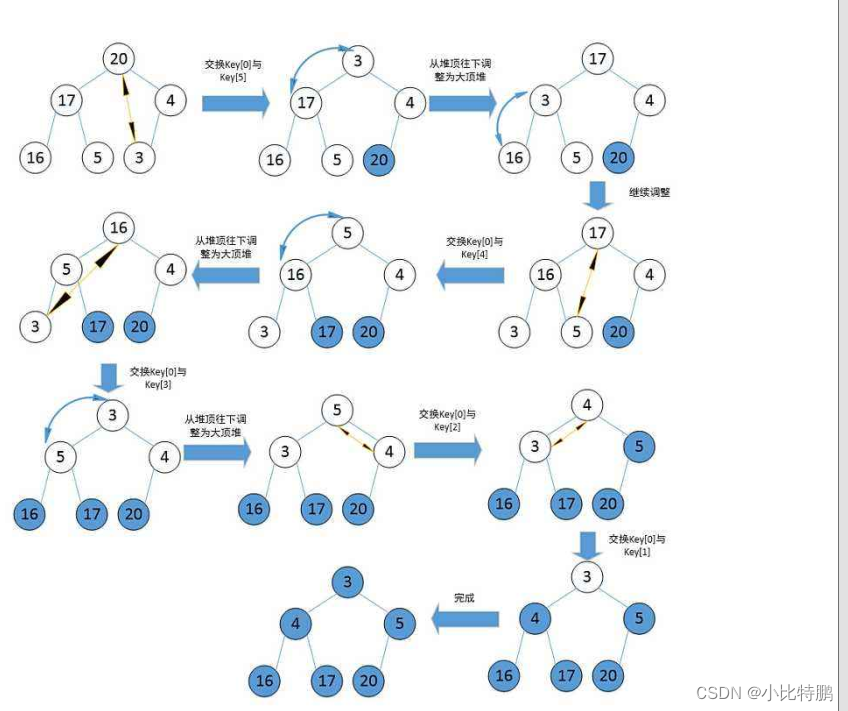
时间复杂度:O(N*logN);
空间复杂度:O(1);
堆排序不稳定
代码实现如下:
//堆排序public static void heapSort(int[] array) {//创建大根堆createHeap(array);int end = array.length - 1;while (end > 0) {swap(array, 0, end);siftDown(array, 0, end);end--;}}private static void createHeap(int[] array) {for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {siftDown(array, parent, array.length);}}private static void siftDown(int[] array, int parent, int len) {int child = (2 * parent) + 1;while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {child = child + 1;}if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = 2 * parent + 1;} else {break;}}}private static void swap(int[] array, int i, int j) {int tmp = array[j];array[j] = array[i];array[i] = tmp;}
到这里就讲完了 数据结构7大排序 当然还有很多排序 如果有兴趣可以去查找一下资料 比如说:
基数排序
计数排序
桶排序
相关文章:

Java七大排序详解
排序 排序的概念 所谓排序 ,就是让一串记录,按照其中某些或者某个关键字的大小,递增或递减的排列起来的操作。 稳定性:就比如在待排序的序列中,存在多个具有相同关键字的记录 ,如果经过排序这些相同的关键…...

图像旋转角度计算并旋转
#!/usr/bin/python3 # -*- coding: utf-8 -*- import cv2 import numpy as np import timedef Rotate(img, angle0.0,fill0):"""旋转:param img:待旋转图像:param angle: 旋转角度:param fill:填充方式,默认0黑色填充:return: img: 旋转后…...
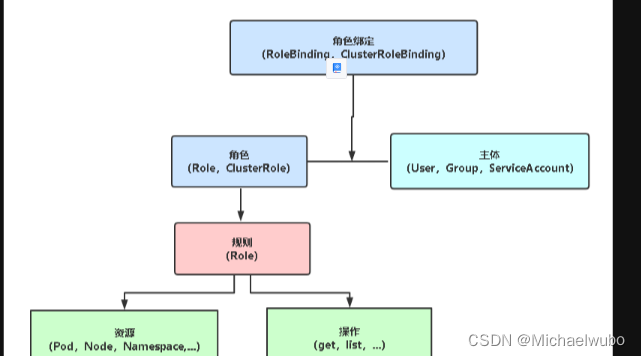
通过curl访问k8s集群获取证书或token的方式
K8S安全控制框架主要由下面3个阶段进行控制,每一个阶段都支持插件方式,通过API Server配置来启用插件。 1. Authentication(认证) 2. Authorization(授权) 3. Admission Control(准入控制&#…...

苍穹外卖-前端部分(持续更新中)
d 第二种:cmd中输入 vue ui进入图形化界面选择npm,vue2进行创建 先将创建的Vue框架导入Vsocde开发工具 然后ctrshiftp 输入npm 点击serve将项目启动 下这种写法跨域会报错: 解决方法:...
windows用mingw(g++)编译opencv,opencv_contrib,并install安装
windows下用mingw编译opencv貌似不支持cuda,选cuda会报错,我无法解决,所以没选cuda,下面两种编译方式支持。 如要用msvc编译opencv,参考我另外一篇文章 https://blog.csdn.net/weixin_44733606/article/details/1357…...
JDWP 协议及实现
JDWP 的协议细节并通过实际调试中的例子展开揭示 JDWP 的实现机制,JDWP 是 Java Debug Wire Protocol 的缩写,它定义了调试器(debugger)和被调试的 Java 虚拟机(target vm)之间的通信协议。 JDWP 协议介绍 这里首先要说明一下 debugger 和 target vm。Target vm 中运行…...
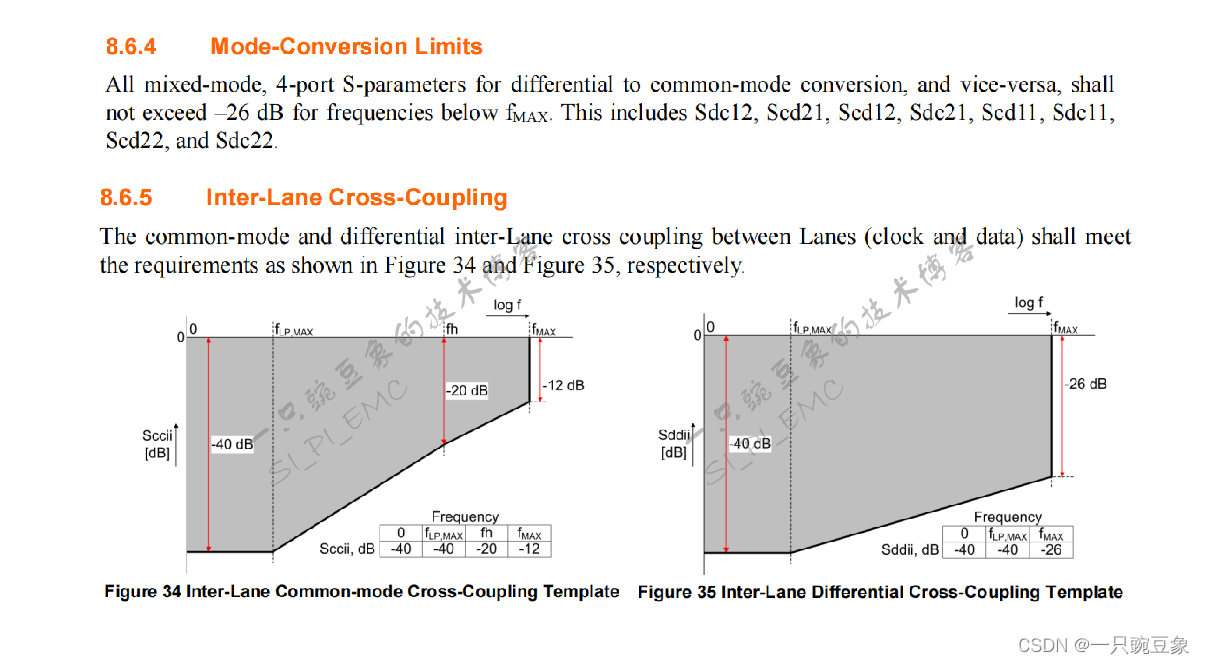
利用ADS建立MIPI D-PHY链路仿真流程
根据MIPI D-PHY v1.2规范中对于互连电气参数的定义,本次仿真实例中,需要重点关注如下的设计参数: 1. 差分信号的插入损耗Sddij和回拨损耗Sddii; 2. 模式转换损耗Sdcxx、Scdxx; 3. 数据线与时钟线之间的串扰耦合(远、近端)。 设计者还可以结合CTS中的补充…...

【大根堆】【C++算法】871 最低加油次数
作者推荐 【动态规划】【map】【C算法】1289. 下降路径最小和 II 本文涉及知识点 大根堆 优先队列 LeetCode:871最低加油次数 汽车从起点出发驶向目的地,该目的地位于出发位置东面 target 英里处。 沿途有加油站,用数组 stations 表示。其中 statio…...
SpringBoot的自动装配原理
一、SpringBootConfiguration注解的作用 SpringBootApplication注解是SpringBoot项目的核心注解,加在启动引导类上。点击进去可以发现SpringBootApplication注解是一个组合注解。其中SpringBootConfiguration和EnableAutoConfiguration是由Spring提供的,剩下的注解是由JDK提供的…...

嵌入式驱动开发需要会哪些技能?
嵌入式驱动开发是指在嵌入式系统中编写驱动程序,实现设备与计算机之间的通信。嵌入式驱动开发是指编写设备驱动程序,实现设备与计算机之间的通信。以下是一些嵌入式驱动开发的具体操作方法: 1)了解硬件设备结构:在进行嵌入式驱动…...
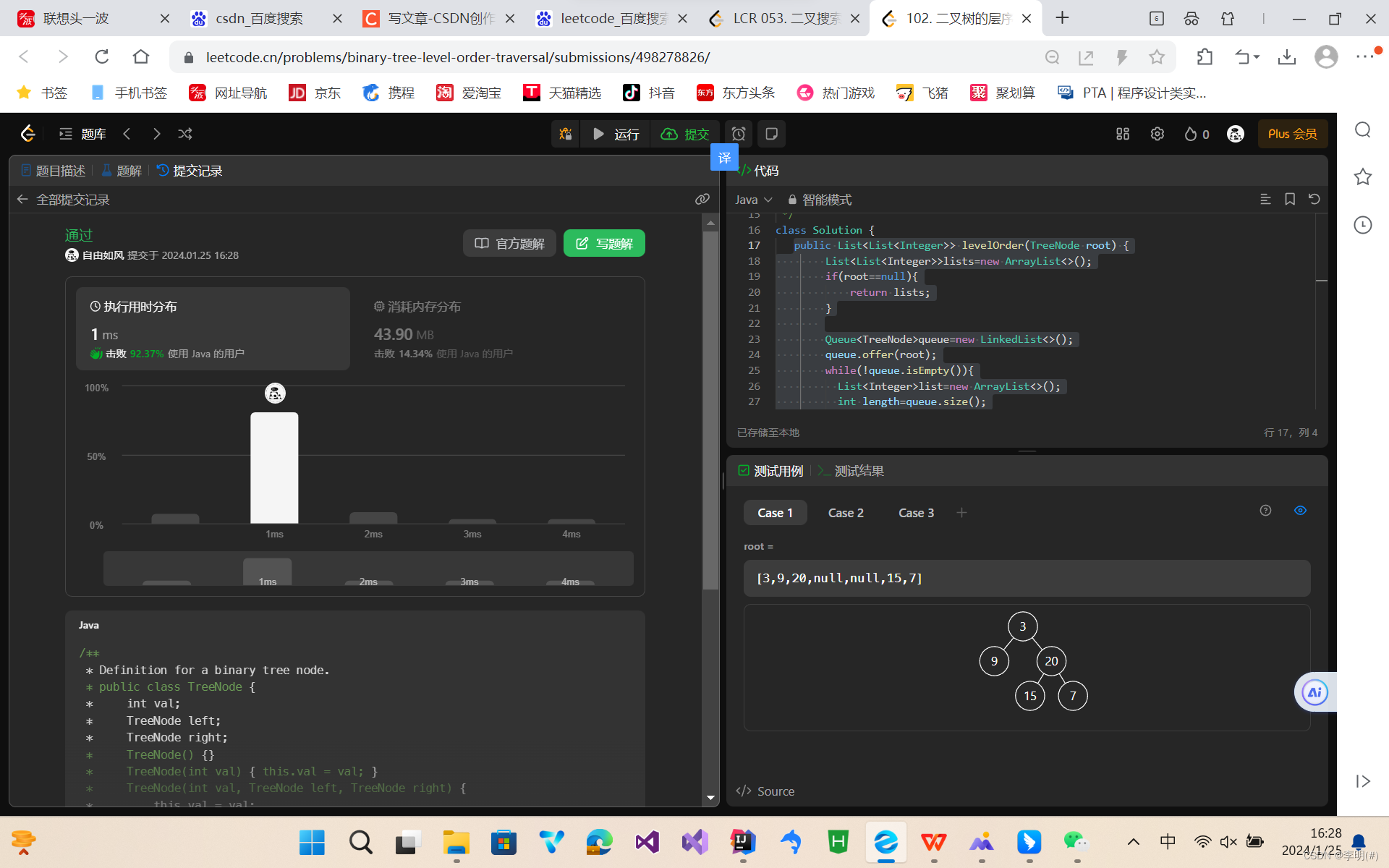
Leetcode:二分搜索树层次遍历
题目: 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例: 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,…...

【fabric.js】toDataURL 性能问题、优化
必要解释:最好看完。。省流版的话,toDataURL 的 multiplier参数不要设置超过500; 情景:在做某些功能的时候涉及到图形的预览,预览的时候是导出为40*40 像素的图片,当碰到某些图形非常小的时候,…...
基于Grafana+Prometheus搭建可视化监控系统实践
基本介绍 Grafana:一个监控仪表系统,可以根据提供的监控数据,生产可视化仪表盘,同时也具有告警通知功能。这里的监控数据来源,目前主要以Prometheus为主(也支持其它数据源),每次展现…...
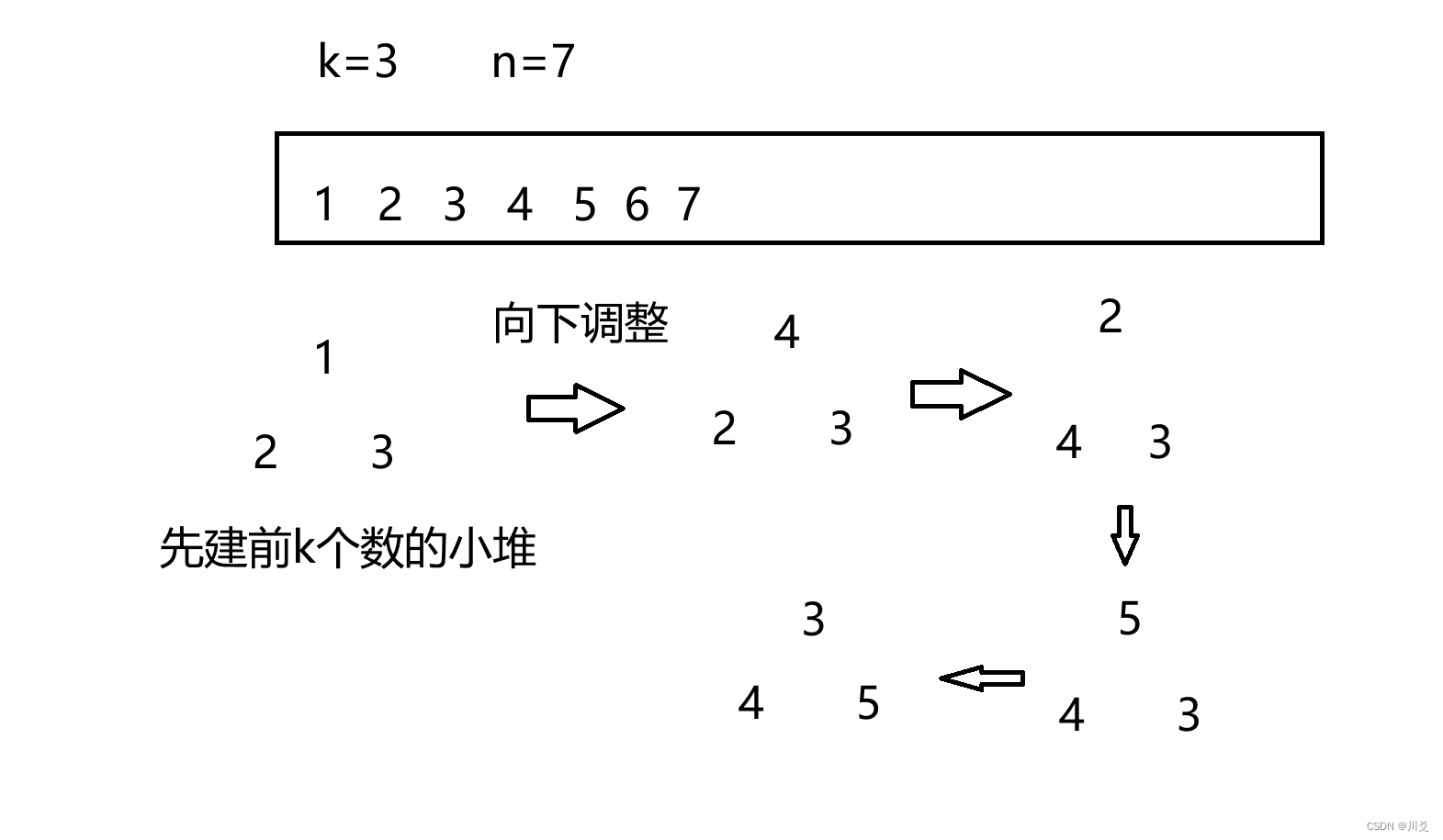
选择排序(堆排序和topK问题)
选择排序 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。 如果我们用扑克牌来举例,那么选择排序就像是提前已经把所有牌都摸完了,而再进行牌…...

webpack tree shaking 摇树原理
Tree-shaking 是指在打包过程中通过静态分析,识别并删除未使用的代码,以减小最终输出文件的大小。Webpack 通过内置的 UglifyJS 插件或者 Terser 插件来实现 Tree-shaking。下面是简要的 webpack Tree-shaking 的原理: 标记未使用的代码&…...
)
开源模型应用落地-业务整合篇(三)
一、前言 在之前的两篇文章中,我们学习了如何构建基本的即时消息(IM)功能。今天,我们将进一步将IM模块与AI服务进行连接,实现用户提问并由模型进行回答,最后将结果展示在用户界面上。 二、术语 2.1. Spring Boot 是一个用于快速构建基于Spring框架的Java应用程序的开源框…...

js打地鼠
文章目录 1实现效果2代码实现 1实现效果 游戏难度:简单,一般,困难,噩梦(控制setInterval的time参数) 按钮功能:结束(可以通过修改gameScore的值来修改判定结束的分数)&am…...

计算机网络体系架构认知--网络协议栈
文章目录 一.计算机网络分层架构各协议层和计算机系统的联系从整体上理解计算机网络通信计算机网络通信的本质 二.Mac地址,IP地址和进程端口号三.局域网通信与跨局域网通信局域网通信跨局域网通信全球互联的通信脉络 四.网络编程概述 一.计算机网络分层架构 实现计算机长距离网…...

Ubuntu 22.04 安装tomcat
tomcat是常用的Java服务容器,这篇文章我们就来讲讲如何安装它。 更新软件包 首先是更新软件包,这是最常规的操作 sudo apt update 然后是开始安装,不多一会就可以安装好了 sudo apt install tomcat9 然后看一下状态 sudo systemctl status tomcat9 发现虽然启动了,但…...

记录:Ubuntu 18.04 X86 上通过CMake 指定编译器工具链交叉编译。
最好是通过 cmake 命令行来设置,要不然你只有在 CMakeFiles.txt 里面自己写判断语句了。 要用 cmake 交叉编译,必须设置连接器,要不然会使用当前系统的 ld,就是 /usr/bin/ld。 但是其它平台是不会ld上的,elf格式都不…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
