Open CASCADE学习|圆柱螺旋线绘制原理探究
1、圆柱螺旋线绘制原理
在OCC中,圆柱面的参数方程为:
设P为(x0,y0,z0),则
x=x0+r*cos(u)
y=y0+r*sin(u)
z=z0+v
但u、v之间有关系时,此方程表达为圆柱螺旋线,u、v之间为线性关系时是等螺距螺旋线,u、v之间为非线性关系时是变螺距螺旋线。

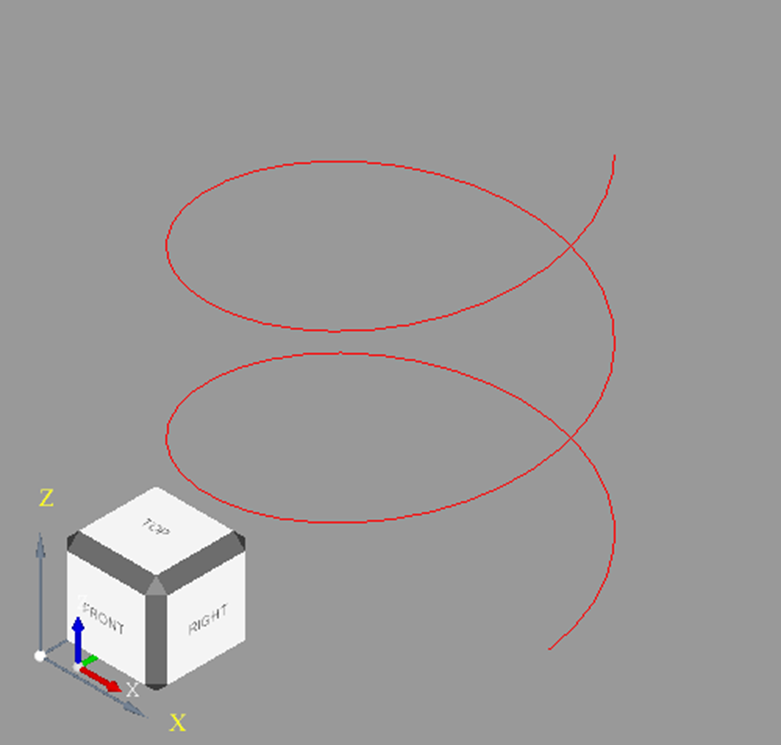
2、Draw Test Harness命令绘制圆柱螺旋线
使用Tcl命令在Draw Test Harness中生成的圆柱螺旋线并到出Brep数据如下:
pload ALL
cylinder aCylinder 6
line aLine2d 0 0 1 1
trim aSegment aLine2d 0 2*pi
mkedge aHelixEdge aSegment aCylinder 0 6*pi
dump aHelixEdge
代码先加载所有模块,然后创建一个圆柱面aCylinder;一条二维直线aLine2d;再将参数范围限定在0到2PI之间;最后使用了用曲面及其上的pcurve来创建边的算法mkedge生成了螺旋线并导出Brep数据。
3、Brep数据
Brep数据如下所示,下面直接在该数据中进行解释说明。
*********** Dump of aHelixEdge *************
Shape : 3, FORWARD
Dump of 3 TShapes
-----------------
Flags : Free, Modified, Checked, Orientable, Closed, Infinite, Convex, Locked
TShape # 1 : EDGE11010000 0000027C9109C6E0
+3 -2
Tolerance : 1e-07
same parametrisation of curves
same range on curves
- PCurve : 1 on surface 1, range : 0 18.8495559215388
UV Points : 0, 0 13.3286488144751, 13.3286488144751
- Polygon 3D : 1
这里存储螺旋线的起点、终点Pcurve以及Polygon 3D
该螺旋线始于Tshape3,终于Tshape2,其是圆柱面上的参数曲线,其参数范围为:
u:[0, 13.3286488144751]
v:[0, 13.3286488144751]
参数由Curve2ds中的1号直线的起点、方向,及范围[0,18.8495559215388]确定
螺旋线的参数方程由参数范围及surface中的1号面确定
TShape # 2 : VERTEX01011010 0000027C910A35A0
Tolerance : 1e-07
- Point 3D : 4.33958778097726, 4.14342586408793, 13.3286488144751
这里存储螺旋线的终点,坐标为(4.33958778097726,4.14342586408793,13.3286488144751)
TShape # 3 : VERTEX01011010 0000027C910A2F20
Tolerance : 1e-07
- Point 3D : 6, 0, 0
这里存储螺旋线的起点,坐标为(6,0,0)
-------
Dump of 1 Curve2ds
-------
1 : Line
Origin :0, 0
Axis :0.707106781186547, 0.707106781186547
这里存储Pcurve的起点及方向,这个方向是归一化后的
-------
Dump of 0 Curves
-------
-------
Dump of 1 Polygon3Ds
-------
1 : Polygon3D with 79 Nodes
with parameters
Deflection : 0.054777818570848
Nodes :
1 : 6 0 0
2 : 5.91147846277275 1.02685071172685 0.171988435739901
3 : 5.64852587194202 2.02340195561871 0.343976871479801
4 : 5.21890121669389 2.96024831566391 0.515965307219702
5 : 4.63528150866612 3.80974609855013 0.687953742959602
6 : 3.91488771909563 4.54682902107328 0.859942178699503
7 : 3.07897663653632 5.14974784544481 1.0319306144394
8 : 2.15221363899269 5.60071213794584 1.2039190501793
9 : 1.16194488819403 5.88641521444077 1.3759074859192
10 : 0.137390421503272 5.99842678308898 1.54789592165911
11 : -0.891218048958075 5.9334416984758 1.71988435739901
12 : -1.89352918885328 5.69337748713017 1.89187279313891
13 : -2.83996762388782 5.28531776672595 2.06386122887881
14 : -3.70260662567498 4.7213032285067 2.23584966461871
15 : -4.45599215071128 4.01797635045298 2.40783810035861
16 : -5.07789391739641 3.19609032470432 2.57982653609851
17 : -5.54996135893326 2.27989668940233 2.75181497183841
18 : -5.85826509678857 1.29642973421194 2.92380340757831
19 : -5.99370795735972 0.274708794695026 3.09579184331821
20 : -5.95229340390531 -0.755118026420635 3.26778027905811
21 : -5.73524346307045 -1.76266344470738 3.43976871479801
22 : -5.34896266632775 -2.71819763708086 3.61175715053791
23 : -4.80484907032021 -3.59352548501371 3.78374558627782
24 : -4.11895793236278 -4.36281853294699 3.95573402201772
25 : -3.31152796508963 -5.00337711315361 4.12772245775762
26 : -2.40638414913624 -5.49630014889888 4.29971089349752
27 : -1.43023472516923 -5.82704287189653 4.47169932923742
28 : -0.41188310904629 -5.98584599739104 4.64368776497732
29 : 0.618622015733548 -5.96802369312068 4.81567620071722
30 : 1.63087334991494 -5.77410184500908 4.98766463645712
31 : 2.59500221211051 -5.40980253975517 5.15965307219702
32 : 3.48255987933138 -4.88587522219627 5.33164150793692
33 : 4.26735702855079 -4.21777950951424 5.50362994367683
34 : 4.92623650974859 -3.42522902154295 5.67561837941673
35 : 5.43975664808373 -2.53160968745753 5.84760681515663
36 : 5.79276491287537 -1.5632896929744 6.01959525089653
37 : 5.97484502603907 -0.548841429573404 6.19158368663643
38 : 5.98062431706958 0.481801596174212 6.36357212237633
39 : 5.80993225539153 1.49822801594453 6.53556055811623
40 : 5.46780548223566 2.47044595335207 6.70754899385613
41 : 4.9643391935641 3.36976799961708 6.87953742959603
42 : 4.31438925931528 4.16965769807366 7.05152586533593
43 : 3.53713386858935 4.8465125601486 7.22351430107583
44 : 2.65550763538804 5.38036050821837 7.39550273681573
45 : 1.69552486285233 5.75544919528003 7.56749117255563
46 : 0.685511934561036 5.96071081227519 7.73947960829553
47 : -0.344728517141907 5.99008866791378 7.91146804403543
48 : -1.36479700275703 5.84271590454862 8.08345647977533
49 : -2.34459417880975 5.52294107669921 8.25544491551523
50 : -3.25520899456837 5.04019983747482 8.42743335125513
51 : -4.06977177559527 4.40873651906849 8.59942178699503
52 : -4.76424707204225 3.6471838226962 8.77141022273493
53 : -5.31814287697335 2.77801302014544 8.94339865847483
54 : -5.71511528768318 1.82687088993449 9.11538709421473
55 : -5.94345076816078 0.821822953225958 9.28737552995463
56 : -5.99641178249436 -0.207474660531981 9.45936396569454
57 : -5.87243560054993 -1.23065028232791 9.63135240143444
58 : -5.57518040972927 -2.21751288586357 9.80334083717434
59 : -5.11341737217911 -3.13894293957327 9.97532927291424
60 : -4.50077181253901 -3.96775164185642 10.1473177086541
61 : -3.75532117304723 -4.67948318591521 10.319306144394
62 : -2.89906159921539 -5.25313638162524 10.4912945801339
63 : -1.95725889562388 -5.67178434141331 10.6632830158738
64 : -0.95770300330158 -5.92307394496026 10.8352714516137
65 : 0.0701120030405293 -5.99959034493436 11.0072598873536
66 : 1.09585820195355 -5.89907575821934 11.1792483230935
67 : 2.08926871665989 -5.62449608672513 11.3512367588334
68 : 3.02103080520639 -5.18395340198907 11.5232251945733
69 : 3.8636507967903 -4.59044687590017 11.6952136303132
70 : 4.59226535242716 -3.86148921180638 11.8672020660531
71 : 5.18537511194659 -3.01858989404074 12.039190501793
72 : 5.62547907946288 -2.08662050371539 12.2111789375329
73 : 5.89959102839457 -1.09308082852379 12.3831673732728
74 : 5.99962268837775 -0.0672874215806556 12.5551558090127
75 : 5.92262240730803 0.960491447360601 12.7271442447526
76 : 5.67086224626782 1.95992892316386 12.8991326804925
77 : 5.25177093741309 2.90153442525559 13.0711211162324
78 : 4.83571236765298 3.55188483728401 13.1998849653538
79 : 4.33958778097726 4.14342586408793 13.3286488144751
这里存储螺旋线的数据点,一共80个点
Parameters :
0 0.243228378394701 0.486456756789402 0.729685135184103 0.972913513578804 1.2161418919735 1.45937027036821 1.70259864876291 1.94582702715761 2.18905540555231 2.43228378394701 2.67551216234171 2.91874054073641 3.16196891913111 3.40519729752581 3.64842567592052 3.89165405431522 4.13488243270992 4.37811081110462 4.62133918949932 4.86456756789402 5.10779594628872 5.35102432468343 5.59425270307813 5.83748108147283 6.08070945986753 6.32393783826223 6.56716621665693 6.81039459505164 7.05362297344634 7.29685135184104 7.54007973023574 7.78330810863044 8.02653648702514 8.26976486541984 8.51299324381454 8.75622162220924 8.99945000060394 9.24267837899865 9.48590675739335 9.72913513578805 9.97236351418275 10.2155918925774 10.4588202709721 10.7020486493668 10.9452770277616 11.1885054061563 11.431733784551 11.6749621629457 11.9181905413404 12.1614189197351 12.4046472981298 12.6478756765245 12.8911040549192 13.1343324333139 13.3775608117086 13.6207891901033 13.864017568498 14.1072459468927 14.3504743252874 14.5937027036821 14.8369310820768 15.0801594604715 15.3233878388662 15.5666162172609 15.8098445956556 16.0530729740503 16.296301352445 16.5395297308397 16.7827581092344 17.0259864876291 17.2692148660237 17.5124432444184 17.7556716228131 17.9989000012078 18.2421283796025 18.4853567579972 18.667456339768 18.8495559215388
这里存储输入的参数
-------
Dump of 0 PolygonOnTriangulations
-------
-------
Dump of 1 surfaces
-------
1 : CylindricalSurface
Origin :0, 0, 0
Axis :0, 0, 1
XAxis :1, 0, -0
YAxis :-0, 1, 0
Radius :6
这里存储确定圆柱面参数方程所需的起点、向量及半径
-------
Dump of 0 Triangulations
-------
-------
Dump of 0 Locations
-------
从这个文件数据可以看出,该螺旋线的参数方程为
x=0+6*cos(u)
y=0+6*sin(u)
z=0+v
v=u,u取6*PI*[0,√2/2]即[0, 13.3286488144751]
此螺旋线螺旋角为45°
4、C++代码绘制圆柱螺旋线
TopoDS_Shape createHelix()
{Handle_Geom_CylindricalSurface aCylinder = new Geom_CylindricalSurface(gp::XOY(), 6.0);gp_Lin2d aLine2d(gp_Pnt2d(0.0, 0.0), gp_Dir2d(1.0, 1.0));Handle(Geom2d_TrimmedCurve) aSegment = GCE2d_MakeSegment(aLine2d, 0.0, M_PI * 2.0);TopoDS_Shape aHelixEdge = BRepBuilderAPI_MakeEdge(aSegment, aCylinder, 0.0, 6.0 * M_PI);//BRepTools::Write(aHelixEdge, "d:/helix.brep");return aHelixEdge;
}
参考文献:1、https://www.cppblog.com/eryar/archive/2015/07/09/211212.html2、https://dev.opencascade.org/doc/occt-7.7.0/overview/html/specification__brep_format.html
相关文章:

Open CASCADE学习|圆柱螺旋线绘制原理探究
1、圆柱螺旋线绘制原理 在OCC中,圆柱面的参数方程为: 设P为(x0,y0,z0),则 xx0r*cos(u) yy0r*sin(u) zz0v 但u、v之间有关系时,此方程表达为圆柱螺旋线,u、v之间为线性关系时是等螺距螺旋线࿰…...

Python学习笔记--认识sys.argv
sys.argv 是 Python 的一个内置模块 sys 中的一个属性。它是一个列表,包含了从命令行传递给脚本的参数。 例如,如果你有一个名为 script.py 的脚本,并且你从终端窗口命令行这样运行它: >>>python script.py arg1 arg2 …...
【C++】入门基础
前言:C是在C的基础之上,容纳进去了面向对象编程思想,并增加了许多有用的库,以及编程范式等。熟悉C语言之后,对C学习有一定的帮助,因此从今天开始们将进入C的学习。 💖 博主CSDN主页:…...
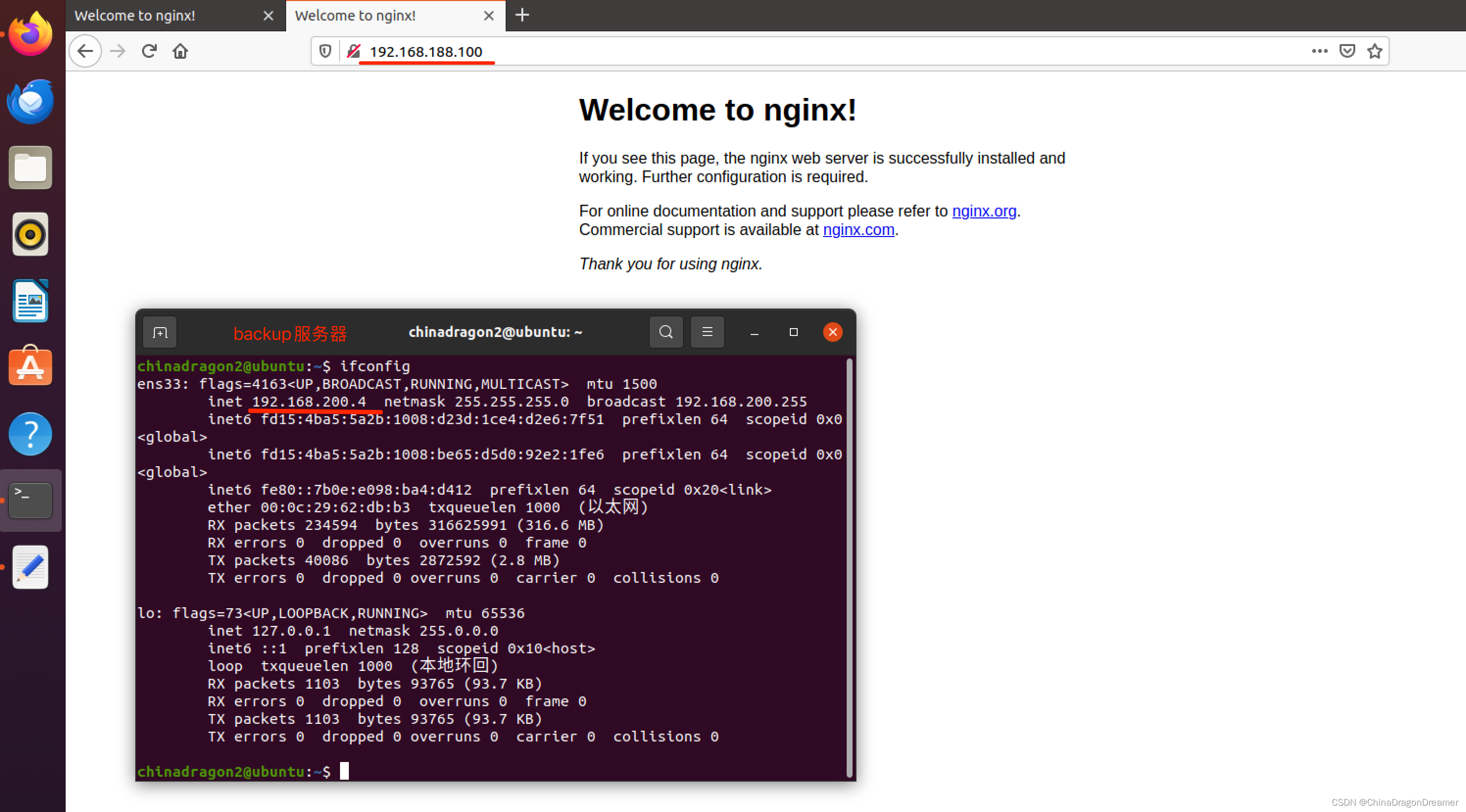
Nginx与keepalived实现集群
提醒一下:下面实例讲解是在mac虚拟机里的Ubuntu系统演示的; Nginx与keepalived实现集群实现的效果 两台服务器都安装Nginx与keepalived: master服务器的ip(192.168.200.2) backup服务器的ip(192.168.200.4) 将 master服务器Nginx与keepalive…...

初识MQRabbitMQ快速入门
一、同步和异步通讯 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,需要实时响应。 异步通讯:就像发邮件,不需要马上回复。 两种方式各有优劣,打电话可以立即得到响应,但是你却不能…...

javaMailSender 发送邮件,基于Spring Boot
目录 引入依赖 配置文件配置 具体代码 MultipartFile 转 File 工具类 引入依赖 <!--邮件--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId></dependency><!--日…...

【汇总】解决Spring-Web与Spring-WebFlux冲突
【汇总】解决Spring-Web与Spring-WebFlux冲突 问题发现问题解决问题一:The bean requestMappingHandlerMapping, defined in class path resource [org/springframework/web/reactive/config/DelegatingWebFluxConfiguration.class],问题二:The Java/XML…...

maven 依赖配置补充
依赖配置补充 依赖范围 import 管理依赖最基本的办法是继承父工程,但是和 Java 类一样,Maven 也是单继承的。如果不同体系的依赖信息封装在不同 POM 中了,没办法继承多个父工程怎么办?这时就可以使用 import 依赖范围。 典型案…...

Pandas ------ 向 Excel 文件中写入含有合并表头的数据
Pandas ------ 向 Excel 文件中写入含有合并表头的数据 推荐阅读引言正文 推荐阅读 Pandas ------ 向 Excel 文件中写入含有 multi-index 和 Multi-column 表头的数据 引言 这里给大家介绍一下如何向 Excel 中写入带有合并表头的数据。 正文 import pandas as pddf1 pd.D…...
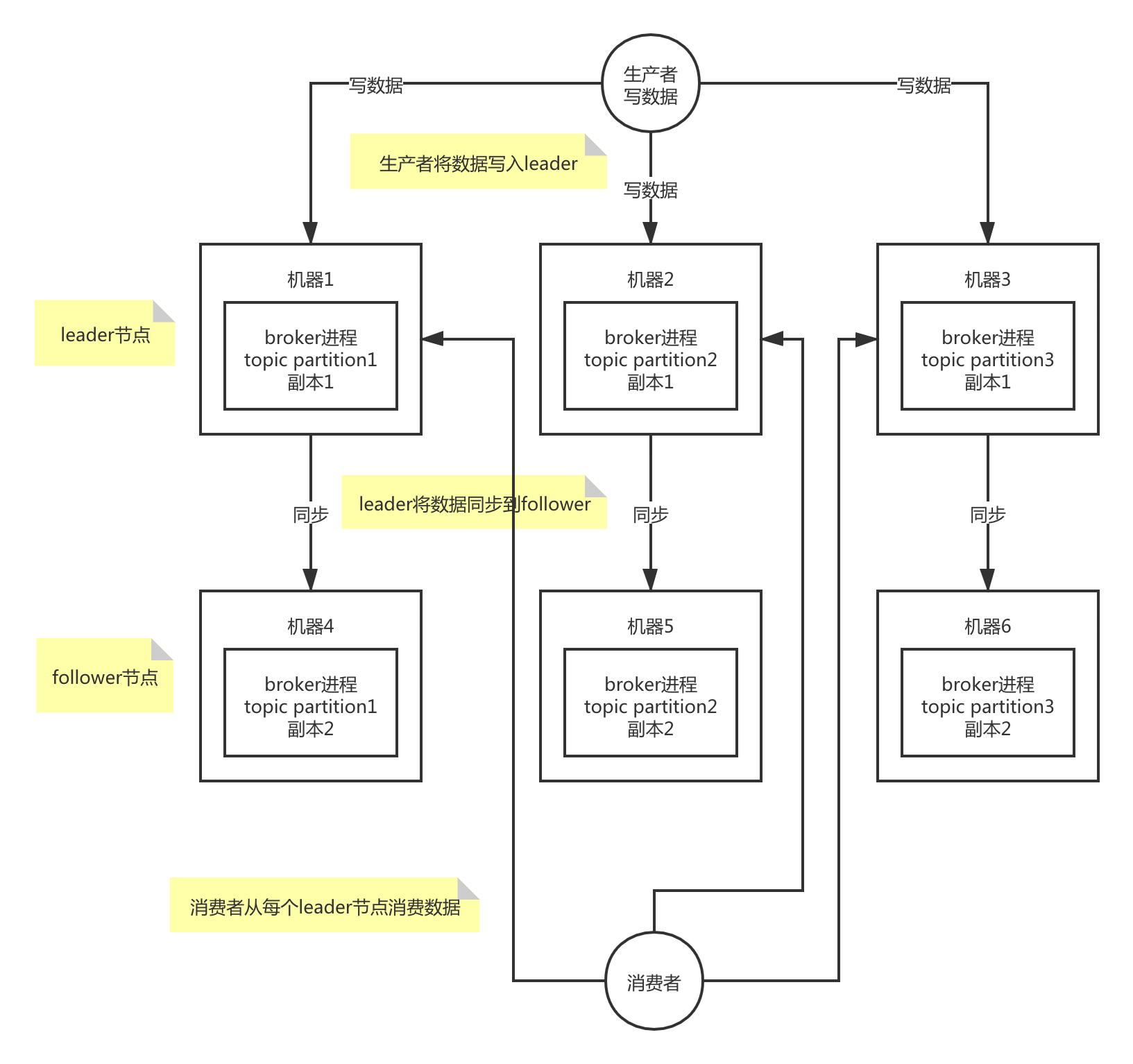
kafka summary
最近整体梳理之前用到的一些东西,回顾Kafka的时候好多东西都忘记了,把一些自己记的比较模糊并且感觉有用的东西整理一遍并且记忆一遍,仅用于记录以备后续回顾 Kafka的哪些场景中使用了零拷贝 生产者发送消息:在 Kafka 生产者发送…...
【新书推荐】2.6节 原码、反码和补码
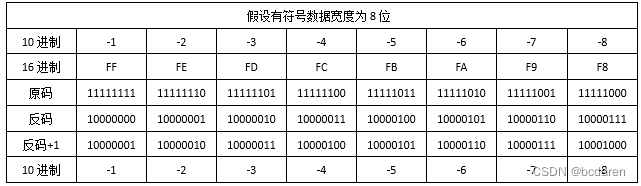
回顾上一节中,我们讲解了整数的编码规则。 无符号整数编码规则:无符号整数全部都是正数,是什么就存什么。 有符号整数编码规则:有符号整数最高有效位为0是正数,最高有效位为1是负数。 本节内容:原码、反…...
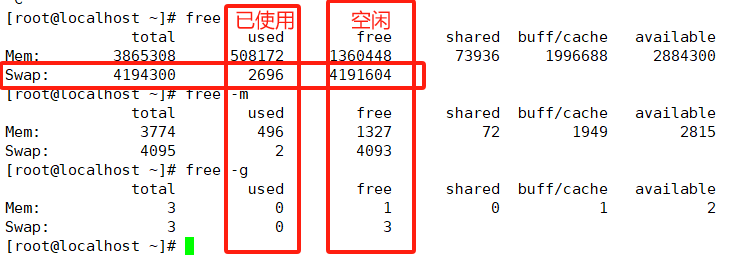
docker 网络及如何资源(CPU/内存/磁盘)控制
安装Docker时,它会自动创建三个网络,bridge(创建容器默认连接到此网络)、 none 、host docker网络模式 Host 容器与宿主机共享网络namespace,即容器和宿主机使用同一个IP、端口范围(容器与宿主机或其他使…...
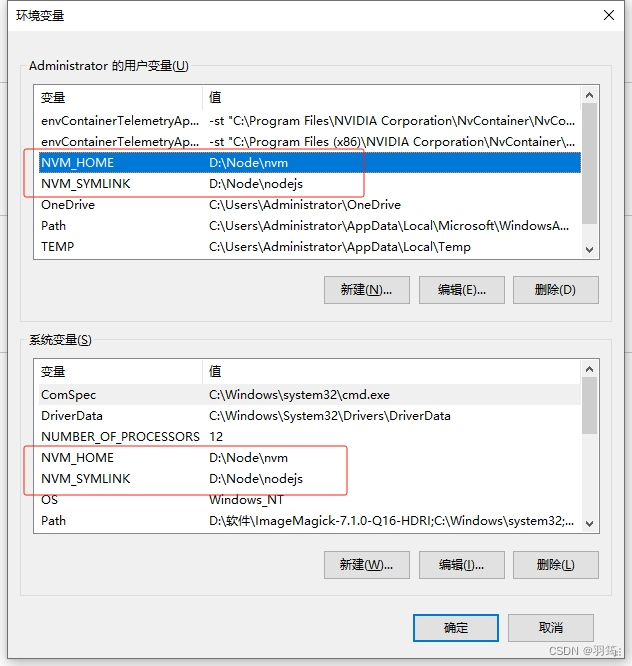
安装 nvm
前言: nvm 即 node 版本管理工具 (node version manager),好处是方便切换 node.js 版本。 通过将多个 node 版本安装在指定路径,然后通过 nvm 命令切换时,就会切换我们环境变量中 node 命令指定的实际执行的软件路径。 使用场景…...

Redis解决方案:NOAUTH Authentication required(连接jedis绑定密码或修改redis密码)
Redis解决方案:NOAUTH Authentication required(连接jedis绑定密码或修改redis密码) Java使用jedis连接redis时出现错误NOAUTH Authentication required 一、问题报错和原因 本地设置了redis的密码,但在远程连接时并没有输入密…...

多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测
多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测 目录 多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测效果一览基本介绍程序设计参考资料 效…...

如何实现无公网IP实现远程访问MongoDB文件数据库
📑前言 本文主要是如何实现无公网IP实现远程访问MongoDB文件数据库的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 &#x…...
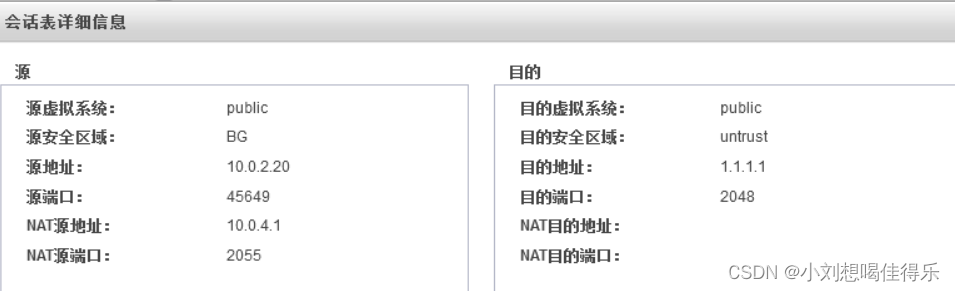
华为防火墙USG6000V1的NAT实验
实验拓扑: 之前实验做过,可以翻找之前的博客,各设备ip和接口已配好,均可可ping通防火墙。 实验要求: 一.生产区在工作时间内可以访问dmz区域,仅可以访问http服务器。 二.办公区全天可以访问dmz区域&…...

spark-flink设计思想之吸星大法-1
Spark和Flink都是大数据处理框架,它们的设计思想有一些不同之处。以下是对它们设计思想的简要对比: 数据模型和计算模型: Spark:Spark使用弹性分布式数据集(RDD)作为其核心数据结构。RDD是只读的、不可变的…...

力扣1312. 让字符串成为回文串的最少插入次数
动态规划 思路: 通过插入字符构造回文串,要想插入次数最少,可以将字符串 s 的逆序 s 进行比较找出最长公共子序列;可以先分析,字符串 s 通过插入得到回文串 ps,其中间的字符应该不会变化: 若 s…...
qemu的安装
1、简介 QEMU(Quick EMUlator)是一个开源的处理器模拟器,它可以在一种硬件平台上模拟另一种硬件平台,从而运行各种不同的操作系统。QEMU通过动态二进制翻译来实现高性能的模拟,这使得它可以在接近原生性能的速度下运行…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
