支持向量机(SVM)详解
支持向量机(support vector machines,SVM)是一种二分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机。
1、线性可分支持向量机与硬间隔最大化
1.1、线性可分支持向量机
考虑一个二分类问题。假设输入空间与特征空间为两个不同的空间,这两个空间的元素一一对应,并将输入空间的输入映射为特征空间中的特征向量,支持向量机的学习是在特征空间进行的。
假设一个特征空间上的训练数据集
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中, x i ∈ X = R n x_i\in \cal{X}=\it{R}^n xi∈X=Rn, y i ∈ Y = { + 1 , − 1 } y_i \in{\cal{Y}}=\{+1,-1\} yi∈Y={+1,−1}, i = 1 , 2 , ⋯ , N i=1,2,\cdots,N i=1,2,⋯,N。 x i x_i xi 为第 i i i 个特征向量,也称为实例, y i y_i yi 为 x i x_i xi 的类标记。
学习的目标是在特征空间中找到一个分离超平面,能够将实例分到不同的类,分离超平面对应于方程 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0,它由法向量 w w w 和截距 b b b 决定。一般地,当训练数据集线性可分时,存在无穷个分离超平面可将数据正确分开,例如感知机利用误分类最小的策略,不过其解有无穷多个,而线性可分支持向量机利用间隔最大化求最优分离超平面,因此其解是唯一的。

1.2、函数间隔和几何间隔
如上图所示, A , B , C A,B,C A,B,C 三个点均在分离超平面的正类一侧,点 A A A 距分离超平面较远,若预测该点为正类,是比较可信的,而预测 C C C 点为正类就不那么可信,点 B B B 介于点 A A A 与 C C C 之间,预测其为正类的可信度也在 A A A 与 C C C 之间。
一般来说,在超平面 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0 确定的情况下, ∣ w ⋅ x + b ∣ \mid w\cdot x+b\mid ∣w⋅x+b∣ 能够相对地表示点 x x x 距离超平面的远近,而 w ⋅ x + b w\cdot x+b w⋅x+b 的符号与类标记 y y y 的符号是否一致能够表示分类是否正确,所以可用量 y ( w ⋅ x + b ) y(w\cdot x+b) y(w⋅x+b) 来表示分类的正确性及确信度,这就是函数间隔(functional margin)的概念,记作 γ ^ i \hat{\gamma}_i γ^i。
但是只要成比例地改变 w w w 和 b b b,例如将它们改为 2 w 2w 2w 和 2 b 2b 2b,超平面并没有改变,但函数间隔却变为原来的 2 倍,所以需要对 w w w 加某些约束,如 ∥ w ∥ = 1 \parallel w\parallel=1 ∥w∥=1,使得间隔是确定的。这时函数间隔就成为了几何间隔(geometric margin),记作 γ i \gamma_i γi。

上图给出了超平面 ( w , b ) (w,b) (w,b) 及其法向量 w w w。点 A A A 表示某一实例 x i x_i xi,其类标记为 y i = + 1 y_i=+1 yi=+1。点 A A A 与超平面 ( w , b ) (w,b) (w,b) 的距离由线段 A B AB AB 给出,记作 γ i \gamma_i γi。
γ i = w ∥ w ∥ ⋅ x i + b ∥ w ∥ \gamma_i=\dfrac{w}{\parallel w\parallel}\cdot x_i+\dfrac{b}{\parallel w\parallel} γi=∥w∥w⋅xi+∥w∥b
其中, ∥ w ∥ \parallel w\parallel ∥w∥ 为 w w w 的 L 2 L_2 L2 范数。这是点 A A A 在超平面正的一侧的情形。如果点 A A A 在超平面负的一侧,即 y i = − 1 y_i=-1 yi=−1,那么点与超平面的距离为
γ i = − ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) \gamma_i=-\Big(\dfrac{w}{\parallel w\parallel}\cdot x_i+\dfrac{b}{\parallel w\parallel}\Big) γi=−(∥w∥w⋅xi+∥w∥b)
一般地,当样本点 ( x i , y i ) (x_i,y_i) (xi,yi) 被超平面 ( w , b ) (w,b) (w,b) 正确分类时,点 x i x_i xi 与超平面 ( w , b ) (w,b) (w,b) 的距离是
γ i = y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) \gamma_i=y_i\Big(\dfrac{w}{\parallel w\parallel}\cdot x_i+\dfrac{b}{\parallel w\parallel}\Big) γi=yi(∥w∥w⋅xi+∥w∥b)
1.3、间隔最大化
支持向量机学习的基本思想是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。间隔最大化的直观解释是:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。也就是说,不仅将正负实例点分开,而且对最难分的实例点(离超平面最近的点)也有足够大的确信度将它们分开。这样的超平面应该对未知的新实例有很好的分类预测能力。
(1)最大间隔分离超平面
求最大间隔分离超平面可以表示为下面的约束最优化问题:
max w , b γ s . t . y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) ≥ γ , i = 1 , 2 , ⋯ , N \begin{aligned} \max_{w,b}\quad &\gamma\\ \rm{s.t.}\quad&y_i\Big(\dfrac{w}{\parallel w\parallel}\cdot x_i+\dfrac{b}{\parallel w\parallel}\Big)\geq\gamma,\quad i=1,2,\cdots,N \end{aligned} w,bmaxs.t.γyi(∥w∥w⋅xi+∥w∥b)≥γ,i=1,2,⋯,N
即希望最大化超平面 ( w , b ) (w,b) (w,b) 关于训练数据集的几何间隔 γ \gamma γ,约束条件表示的是超平面 ( w , b ) (w,b) (w,b) 关于每个训练样本的几何间隔至少是 γ \gamma γ。
考虑几何间隔和函数间隔的关系,可以改写为
max w , b γ ^ ∥ w ∥ s . t . y i ( w ⋅ x i + b ) ≥ γ ^ , i = 1 , 2 , ⋯ , N \begin{aligned} \max_{w,b}\quad &\dfrac{\hat{\gamma}}{\parallel w\parallel}\\ \rm{s.t.}\quad&y_i(w\cdot x_i+b)\geq\hat{\gamma},\quad i=1,2,\cdots,N \end{aligned} w,bmaxs.t.∥w∥γ^yi(w⋅xi+b)≥γ^,i=1,2,⋯,N
函数间隔 γ ^ \hat{\gamma} γ^ 的取值并不影响最优化问题的解,事实上,假设将 w w w 和 b b b 按比例改变为 λ w \lambda w λw 和 λ b \lambda b λb,这时函数间隔成为 λ γ ^ \lambda\hat{\gamma} λγ^。函数间隔的这一改变对上面最优化问题的不等式约束没有影响,对目标函数的优化也没有影响,即产生一个等价的最优化问题。这样,就可以取 γ ^ = 1 \hat{\gamma}=1 γ^=1,将其带入上面最优化问题,而最大化 1 ∥ w ∥ \dfrac{1}{\parallel w\parallel} ∥w∥1 和最小化 1 2 ∥ w ∥ 2 \dfrac{1}{2}\parallel w\parallel^2 21∥w∥2 是等价的,于是:
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \min_{w,b}\quad &\dfrac{1}{2}\parallel w\parallel^2\\ \rm{s.t.}\quad&y_i(w\cdot x_i+b)-1\geq0,\quad i=1,2,\cdots,N \end{aligned} w,bmins.t.21∥w∥2yi(w⋅xi+b)−1≥0,i=1,2,⋯,N
如果求出了上述优化问题的解 w ∗ , b ∗ w^\ast,b^\ast w∗,b∗,那么就可以得到最大间隔分离超平面 w ∗ ⋅ x + b ∗ = 0 w^\ast\cdot x+b^\ast=0 w∗⋅x+b∗=0 及分类决策函数 f ( x ) = s i g n ( w ∗ ⋅ x + b ∗ ) f(x)= {sign} (w^\ast\cdot x+b^\ast) f(x)=sign(w∗⋅x+b∗),即线性可分支持向量机模型。
综上所述,就是线性可分支持向量机的学习算法——最大间隔法(maximum margin method)。
(2)支持向量和间隔边界
在线性可分情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量(support vector)。支持向量是使约束条件 y i ( w ⋅ x i + b ) − 1 ≥ 0 y_i(w\cdot x_i+b)-1\geq0 yi(w⋅xi+b)−1≥0 等号成立的点,即
y i ( w ⋅ x i + b ) − 1 = 0 y_i(w\cdot x_i+b)-1=0 yi(w⋅xi+b)−1=0
对 y i = + 1 y_i=+1 yi=+1 的正例点,支持向量在超平面
H 1 : w ⋅ x + b = 1 H_1:w\cdot x+b=1 H1:w⋅x+b=1
上,对 y i = − 1 y_i=-1 yi=−1 的负例点,支持向量在超平面
H 2 : w ⋅ x + b = − 1 H_2:w\cdot x+b=-1 H2:w⋅x+b=−1
上。如下图所示,在 H 1 H_1 H1 和 H 2 H_2 H2 上的点就是支持向量。注意到 H 1 H_1 H1 和 H 2 H_2 H2 平行,并且并没有实例点落在它们中间。在 H 1 H_1 H1 和 H 2 H_2 H2 之间形成一条长带,长带的宽度称为间隔(margin),间隔依赖于分离超平面的法向量 w w w,等于 2 ∥ w ∥ \dfrac{2}{\parallel w\parallel} ∥w∥2。 H 1 H_1 H1 和 H 2 H_2 H2 称为间隔边界。

在决定分离超平面时只有支持向量起作用,而其他实例点并不起作用。如果移动支持向量将改变所求的解;但是如果在间隔边界以外移动其他实例点,甚至去掉这些点,则解是不会改变的。由于支持向量在确定分离超平面中起决定性作用,所以将这种分类模型称为支持向量机。支持向量的个数一般很少,所以支持向量机由很少的 “ 重要的 ” 的训练样本确定。
1.4、学习的对偶算法
为了求解线性可分支持向量机的最优化问题,首先构建拉格朗日函数(Lagrange function),即对每个不等式约束引入拉格朗日乘子(Lagrange multiplier) α i ≥ 0 , i = 1 , 2 , ⋯ , N \alpha_i\geq0,\ i=1,2,\cdots,N αi≥0, i=1,2,⋯,N,定义拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w,b,\alpha)=\dfrac{1}{2}\parallel w\parallel^2-\sum_{i=1}^N\alpha_iy_i(w\cdot x_i+b)+\sum_{i=1}^N\alpha_i L(w,b,α)=21∥w∥2−i=1∑Nαiyi(w⋅xi+b)+i=1∑Nαi
其中, α = ( α 1 , α 2 , ⋯ , α N ) T \alpha=(\alpha_1,\alpha_2,\cdots,\alpha_N)^T α=(α1,α2,⋯,αN)T 为拉格朗日乘子向量。
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
max α min w , b L ( w , b , α ) \max_\alpha\min_{w,b}L(w,b,\alpha) αmaxw,bminL(w,b,α)
所以,为了得到对偶问题的解,需要先求 L ( w , b , α ) L(w,b,\alpha) L(w,b,α) 对 w , b w,b w,b 的极小,再求对 α \alpha α 的极大。
(1)求 min w , b L ( w , b , α ) \min_{w,b}L(w,b,\alpha) minw,bL(w,b,α)
将 L ( w , b , α ) L(w,b,\alpha) L(w,b,α) 分别对 w , b w,b w,b 求偏导并令其等于 0。
∇ w L ( w , b , α ) = w − ∑ i = 1 N α i y i x i = 0 ∇ b L ( w , b , α ) = − ∑ i = 1 N α i y i = 0 \begin{aligned} &\nabla_wL(w,b,\alpha)=w-\sum_{i=1}^N\alpha_iy_ix_i=0\\ &\nabla_bL(w,b,\alpha)=-\sum_{i=1}^N\alpha_iy_i=0 \end{aligned} ∇wL(w,b,α)=w−i=1∑Nαiyixi=0∇bL(w,b,α)=−i=1∑Nαiyi=0
得
w = ∑ i = 1 N α i y i x i ∑ i = 1 N α i y i = 0 \begin{aligned} &w=\sum_{i=1}^N\alpha_iy_ix_i\\ &\sum_{i=1}^N\alpha_iy_i=0 \end{aligned} w=i=1∑Nαiyixii=1∑Nαiyi=0
将其代入拉格朗日函数,即得
L ( w , b , α ) = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i y i ( ( ∑ i = 1 N α j y j x j ) ⋅ x i + b ) + ∑ i = 1 N α i = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \begin{aligned} L(w,b,\alpha)&=\dfrac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_iy_i\Big(\Big(\sum_{i=1}^N\alpha_jy_jx_j\Big)\cdot x_i+b\Big)+\sum_{i=1}^N\alpha_i\\ &=-\dfrac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i \end{aligned} L(w,b,α)=21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαiyi((i=1∑Nαjyjxj)⋅xi+b)+i=1∑Nαi=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
即
min w , b L ( w , b , α ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \min_{w,b}L(w,b,\alpha)=-\dfrac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i w,bminL(w,b,α)=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
(2)求 min w , b L ( w , b , α ) \min_{w,b}L(w,b,\alpha) minw,bL(w,b,α) 对 α \alpha α 的极大,即是对偶问题
max α − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i s . t . ∑ i = 1 N α i y i = 0 α i ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \max_\alpha\quad&-\dfrac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i\\ \rm{s.t.}\quad&\sum_{i=1}^N\alpha_iy_i=0\\ &\alpha_i\geq 0,\quad i=1,2,\cdots,N \end{aligned} αmaxs.t.−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαii=1∑Nαiyi=0αi≥0,i=1,2,⋯,N
将上述目标函数由求极大转换为求极小,即
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s . t . ∑ i = 1 N α i y i = 0 α i ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \min_\alpha\quad&\dfrac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\\ \rm{s.t.}\quad&\sum_{i=1}^N\alpha_iy_i=0\\ &\alpha_i\geq 0,\quad i=1,2,\cdots,N \end{aligned} αmins.t.21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=0αi≥0,i=1,2,⋯,N
上述即对偶最优化问题,假设对偶最优化问题对 α \alpha α 的解为 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^\ast=(\alpha_1^\ast,\alpha_2^\ast,\cdots,\alpha_N^\ast)^T α∗=(α1∗,α2∗,⋯,αN∗)T,可以由 α ∗ \alpha^\ast α∗ 求得原始最优化问题对 ( w , b ) (w,b) (w,b) 的解 w ∗ , b ∗ w^\ast,b^\ast w∗,b∗,
w ∗ = ∑ i = 1 N α i ∗ y i x i b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) \begin{aligned} w^\ast&=\sum_{i=1}^N\alpha_i^\ast y_ix_i\\ b^\ast&=y_j-\sum_{i=1}^N\alpha_i^\ast y_i(x_i\cdot x_j) \end{aligned} w∗b∗=i=1∑Nαi∗yixi=yj−i=1∑Nαi∗yi(xi⋅xj)
从而得到分离超平面及分类决策函数。这种算法称为线性可分支持向量机的对偶学习算法,是线性可分支持向量机学习的基本算法。
2、线性支持向量机与软间隔最大化
2.1、线性支持向量机
上一节的方法对线性不可分训练数据是不适用的,因为这时上述方法中的不等式约束并不能都成立。
假设一个特征空间上的训练数据集
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中, x i ∈ X = R n x_i\in \cal{X}=\it{R}^n xi∈X=Rn, y i ∈ Y = { + 1 , − 1 } y_i \in{\cal{Y}}=\{+1,-1\} yi∈Y={+1,−1}, i = 1 , 2 , ⋯ , N i=1,2,\cdots,N i=1,2,⋯,N。 x i x_i xi 为第 i i i 个特征向量, y i y_i yi 为 x i x_i xi 的类标记。通常情况下,训练数据中有一些特异点(outlier),将这些特异点除去后,剩下大部分的样本点组成的集合是线性可分的。
线性不可分意味着某些样本点 ( x i , y i ) (x_i,y_i) (xi,yi) 不能满足函数间隔大于 1 的约束条件,为了解决这个问题,可以对每个样本点 ( x i , y i ) (x_i,y_i) (xi,yi) 引入一个松弛变量 ξ i ≥ 0 \xi_i\geq0 ξi≥0,使函数间隔加上松弛变量大于等于 1。这样,约束条件变为
y i ( w ⋅ x i + b ) ≥ 1 − ξ i y_i(w\cdot x_i+b)\geq 1-\xi_i yi(w⋅xi+b)≥1−ξi
同时,对每个松弛变量 ξ i \xi_i ξi,支付一个代价 ξ i \xi_i ξi。目标函数由原来的 1 2 ∥ w ∥ 2 \dfrac{1}{2}\parallel w\parallel^2 21∥w∥2 变成
1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i \dfrac{1}{2}\parallel w\parallel^2+C\sum_{i=1}^N\xi_i 21∥w∥2+Ci=1∑Nξi
这里, C > 0 C>0 C>0 称为惩罚参数, C C C 值大时对误分类的惩罚增大, C C C 值小时对误分类的惩罚减小。最小化上式目标函数包含两层含义:使 1 2 ∥ w ∥ 2 \dfrac{1}{2}\parallel w\parallel^2 21∥w∥2 尽量小即间隔尽量大,同时使误分类点的个数尽量小, C C C 是调和二者的系数。
上述的思路,我们称为软间隔最大化。线性不可分的线性支持向量机的学习问题变成如下问题(原始问题):
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i s . t . y i ( w ⋅ x i + b ) ≥ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ≥ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} \min_{w,b,\xi}\quad &\dfrac{1}{2}\parallel w\parallel^2+C\sum_{i=1}^N\xi_i\\ \rm{s.t.}\quad&y_i(w\cdot x_i+b)\geq1-\xi_i,\quad i=1,2,\cdots,N\\ &\xi_i\geq0,\quad i=1,2,\cdots,N \end{aligned} w,b,ξmins.t.21∥w∥2+Ci=1∑Nξiyi(w⋅xi+b)≥1−ξi,i=1,2,⋯,Nξi≥0,i=1,2,⋯,N
设上述问题的解是 w ∗ , b ∗ w^\ast,b^\ast w∗,b∗,于是得到分类超平面 w ∗ ⋅ x + b ∗ = 0 w^\ast\cdot x+b^\ast=0 w∗⋅x+b∗=0 及分类决策函数 f ( x ) = s i g n ( w ∗ ⋅ x + b ∗ ) f(x)=sign(w^\ast\cdot x+b^\ast) f(x)=sign(w∗⋅x+b∗)。称这样的模型为训练样本线性不可分时的线性支持向量机,简称线性支持向量机。
2.2、学习的对偶算法
原始问题的对偶问题是
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s . t . ∑ i = 1 N α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N \begin{aligned} \min_\alpha\quad&\dfrac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\\ \rm{s.t.}\quad&\sum_{i=1}^N\alpha_iy_i=0\\ &0\leq\alpha_i\leq C,\quad i=1,2,\cdots,N \end{aligned} αmins.t.21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=00≤αi≤C,i=1,2,⋯,N
2.3、支持向量
在线性不可分的情况下,对偶问题的解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^\ast=(\alpha_1^\ast,\alpha_2^\ast,\cdots,\alpha_N^\ast)^T α∗=(α1∗,α2∗,⋯,αN∗)T 中对应于 α i ∗ > 0 \alpha_i^\ast>0 αi∗>0 的样本点 ( x i , y i ) (x_i,y_i) (xi,yi) 的实例 x i x_i xi 称为支持向量(软间隔的支持向量)。

如上图所示,这时的支持向量要比线性可分时的情况复杂一些,软间隔的支持向量 x i x_i xi 或者在间隔边界上,或者在间隔边界与分离超平面之间,或者在分离超平面误分一侧。若 α i ∗ < C \alpha_i^\ast<C αi∗<C,则 ξ i = 0 \xi_i=0 ξi=0,支持向量 x i x_i xi 刚好落在间隔边界上;若 α i ∗ = C , 0 < ξ i < 1 \alpha_i^\ast=C,0<\xi_i<1 αi∗=C,0<ξi<1,则分类正确, x i x_i xi 在间隔边界与分离超平面之间;若 α i ∗ = C , ξ i = 1 \alpha_i^\ast=C,\xi_i=1 αi∗=C,ξi=1,则 x i x_i xi 在分离超平面上;若 α i ∗ = C , ξ i > 1 \alpha_i^\ast=C,\xi_i>1 αi∗=C,ξi>1,则 x i x_i xi 位于分离超平面误分一侧。
3、非线性支持向量机与核函数
对解线性分类问题,线性分类支持向量机是一种有效的方法,但是有时分类问题是非线性的,这时可以使用非线性支持向量机。
3.1、核技巧
(1)非线性分类问题

如左图所示,无法用直线(线性模型)将正负实例正确分开,但可以用一条椭圆曲线(非线性模型)将它们正确分开。
一般来说,对给定的一个训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中,实例 x i x_i xi 属于输入空间, x i ∈ X = R n x_i\in \cal{X} =R^n xi∈X=Rn,对应的标记有两类 y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , ⋯ , N y_i\in \cal{Y}=\{-1,+1\},i=1,2,\cdots,\it N yi∈Y={−1,+1},i=1,2,⋯,N。如果能用 R n R^n Rn 的一个超曲面将正负实例正确分开,则称这个问题为非线性可分问题。
分线性问题往往不好求解,所以采用的方法是进行一个非线性映射,将非线性问题转换为线性问题,通过解线性问题的方法求解非线性问题,如上图所示,将左图中椭圆变换成右图的直线,将非线性分类问题变换为线性分类问题。
设原空间为 X ⊂ R 2 \cal{X} \subset \it{R}^2 X⊂R2, x = ( x ( 1 ) , x ( 2 ) ) T ∈ X x=\big(x^{(1)},x^{(2)}\big)^T\in\cal{X} x=(x(1),x(2))T∈X,新空间为 Z ⊂ R 2 \cal{Z} \subset \it{R}^2 Z⊂R2, z = ( z ( 1 ) , z ( 2 ) ) T ∈ Z z=\big(z^{(1)},z^{(2)}\big)^T\in\cal{Z} z=(z(1),z(2))T∈Z,定义从原空间到新空间的变换(映射):
z = ϕ ( x ) = ( ( x ( 1 ) ) 2 , ( x ( 2 ) ) 2 ) T z=\phi(x)=\big((x^{(1)})^2,(x^{(2)})^2\big)^T z=ϕ(x)=((x(1))2,(x(2))2)T
经过变换 z = ϕ ( x ) z=\phi(x) z=ϕ(x),原空间 X ⊂ R 2 \cal{X} \subset \it{R}^2 X⊂R2 变换为新空间 Z ⊂ R 2 \cal{Z} \subset \it{R}^2 Z⊂R2,原空间中的点相应地变换为新空间中的点,原空间中的椭圆
w 1 ( x ( 1 ) ) 2 + w 2 ( x ( 2 ) ) 2 + b = 0 w_1(x^{(1)})^2+w_2(x^{(2)})^2+b=0 w1(x(1))2+w2(x(2))2+b=0
变换成为新空间中的直线
w 1 z ( 1 ) + w 2 z ( 2 ) + b = 0 w_1z^{(1)}+w_2z^{(2)}+b=0 w1z(1)+w2z(2)+b=0
在变换后的新空间里,直线 w 1 z ( 1 ) + w 2 z ( 2 ) + b = 0 w_1z^{(1)}+w_2z^{(2)}+b=0 w1z(1)+w2z(2)+b=0 可以将变换后的正负实例点正确分开。这样原空间的非线性可分问题就变成了新空间的线性可分问题。
(2)核函数的定义
设 X \cal X X 是输入空间(欧式空间 R n R^n Rn 的子集或离散集合),又设 H \cal H H 为特征空间(希尔伯特空间),如果存在一个从 X \cal X X 到 H \cal H H 的映射
ϕ ( x ) : X → H \phi(x):\cal{X}\rightarrow\cal{H} ϕ(x):X→H
使得对所有 x , z ∈ X x,z\in\cal{X} x,z∈X,函数 K ( x , z ) K(x,z) K(x,z) 满足条件
K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) K(x,z)=\phi(x)\cdot\phi(z) K(x,z)=ϕ(x)⋅ϕ(z)
则称 K ( x , z ) K(x,z) K(x,z) 为核函数, ϕ ( x ) \phi(x) ϕ(x) 为映射函数,式中 ϕ ( x ) ⋅ ϕ ( z ) \phi(x)\cdot\phi(z) ϕ(x)⋅ϕ(z) 为 ϕ ( x ) \phi(x) ϕ(x) 与 ϕ ( z ) \phi(z) ϕ(z) 的内积。
(3)核技巧在支持向量机中的应用
我们注意到在线性支持向量机的对偶问题中,无论是目标函数还是决策函数(分离超平面)都只涉及输入实例域实例之间的内积。在对偶问题的目标函数中的内积 x i ⋅ x j x_i\cdot x_j xi⋅xj 可以用核函数 K ( x i , x j ) = ϕ ( x i ) ⋅ ϕ ( x j ) K(x_i,x_j)=\phi(x_i)\cdot\phi(x_j) K(xi,xj)=ϕ(xi)⋅ϕ(xj) 来代替,此时对偶问题的目标函数成为
W ( α ) = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i W(\alpha)=\dfrac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_{i=1}^N\alpha_i W(α)=21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)−i=1∑Nαi
同样,分类决策函数中的内积也可以用核函数代替,而分类决策函数式成为
f ( x ) = s i g n ( ∑ i = 1 N s α i ∗ y i ϕ ( x i ) ⋅ ϕ ( x ) + b ∗ ) = s i g n ( ∑ i = 1 N s α i ∗ y i K ( x i , x ) + b ∗ ) \begin{aligned} f(x)&=sign\Big(\sum_{i=1}^{N_s}\alpha_i^\ast y_i\phi(x_i)\cdot\phi(x)+b^\ast\Big)\\ &=sign\Big(\sum_{i=1}^{N_s}\alpha_i^\ast y_iK(x_i,x)+b^\ast\Big) \end{aligned} f(x)=sign(i=1∑Nsαi∗yiϕ(xi)⋅ϕ(x)+b∗)=sign(i=1∑Nsαi∗yiK(xi,x)+b∗)
3.2、常用核函数
- 多项式核函数(polynomial kernel function)
K ( x , z ) = ( x ⋅ z + 1 ) p K(x,z)=(x\cdot z +1)^p K(x,z)=(x⋅z+1)p - 高斯核函数(Gaussian kernel function)
K ( x , z ) = exp ( − ∥ x − z ∥ 2 σ 2 ) K(x,z)=\exp\Big(-\dfrac{\parallel x-z\parallel}{2\sigma^2}\Big) K(x,z)=exp(−2σ2∥x−z∥)
3.3、非线性支持向量分类机
如上所述,利用核技巧可以将线性分类的学习问题应用到非线性分类问题中去。将线性支持向量机扩展到非线性支持向量机,只需将线性支持向量机对偶形式中的内积换成核函数。
相关文章:

支持向量机(SVM)详解
支持向量机(support vector machines,SVM)是一种二分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机。 1、线性可分支持向量机与硬间隔最大化 1.1、线性可分支持向量机 考虑一个二分…...

huggingface学习|云服务器部署Grounded-Segment-Anything:bug总会一个一个一个一个又一个的解决的
文章目录 一、环境部署(一)模型下载(二)环境配置(三)库的安装 二、运行(一) 运行grounding_dino_demo.py文件(二)运行grounded_sam_demo.py文件(三…...

【最佳实践】Go 组合模式对业务解耦
在 Go 语言中,组合模式(Composition)是通过嵌入结构体(embedding structs)来实现的。它允许我们构建复杂的对象,通过将简单对象组合成树形结构来表示整个部分的层次结构。在 Go 中,这种模式不仅…...

arm 汇编调用C
arm64 汇编调用C函数 main.s .section .text .globl main main:stp x29, x30, [sp, -16]! //store fp x29 lr x30mov x0, #0mov x1, #1bl addmov x1, x0 // x0 return ldp x29, x30, [sp], 16 //restore fp lrretadd.c #include <stdio.h> int add(int a, int…...
Vue3+Vite使用Puppeteer进行SEO优化(SSR+Meta)
1. 背景 【笑小枫】https://www.xiaoxiaofeng.com上线啦 资源持续整合中,程序员必备网站,快点前往围观吧~ 我的个人博客【笑小枫】又一次版本大升级,虽然知道没有多少访问量,但我还是整天没事瞎折腾。因为一些功能在Halo上不太好实…...

uni-app学习与快速上手
文章目录 一、uni-app二、学习与快速上手三、案例四、常见问题五、热门文章 一、uni-app uni-app是一种基于Vue.js开发框架的跨平台应用开发框架,可以用于同时开发iOS、Android、H5和小程序等多个平台的应用。uni-app的设计理念是一套代码可以编译到多个平台运行&a…...

orchestrator介绍3.4 web API 的使用
目录 使用 web API API使用简单举例 查看所有的API 实例 JSON 详解 API使用举例 使用 web API orchestrator提供精心设计的 Web API。 敏锐的 Web 开发人员会注意到(通过Firebug or Developer Tools)Web 界面如何完全依赖于 JSON API 请求。 开发人员可…...
市场复盘总结 20240122
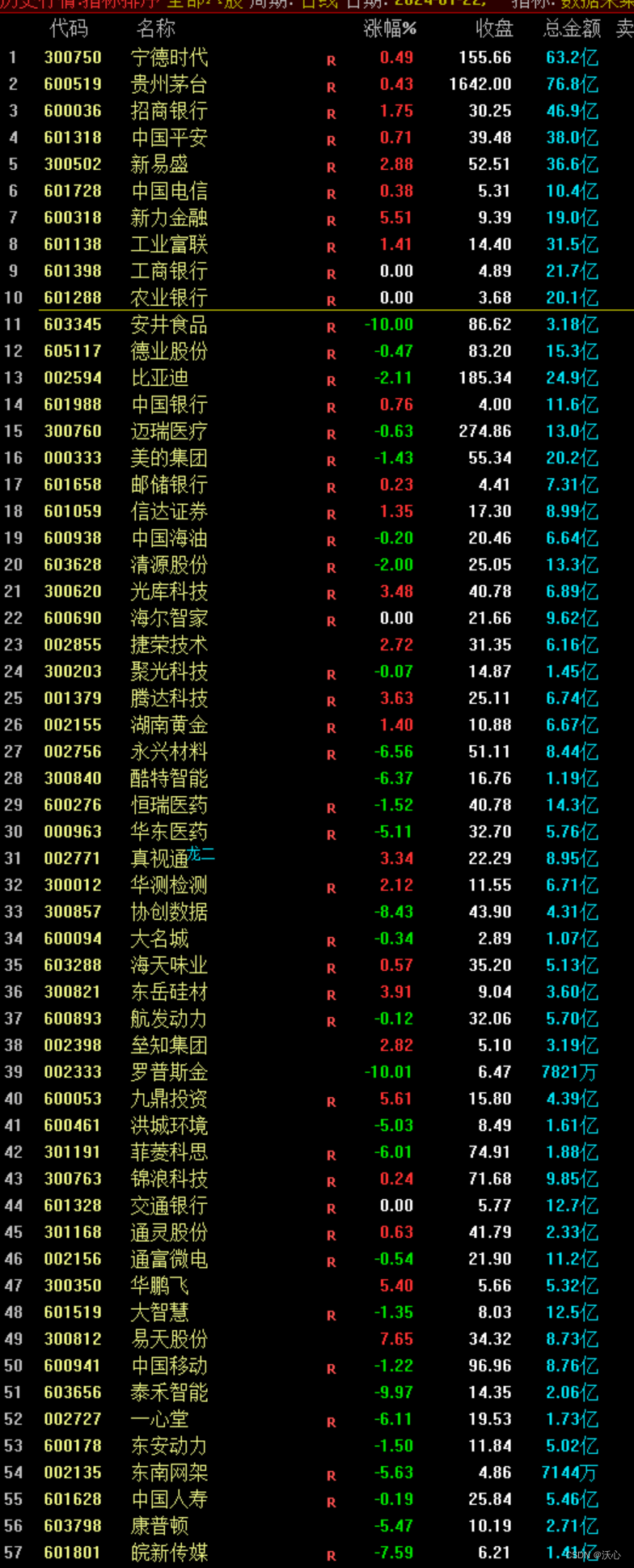
仅用于记录当天的市场情况,用于统计交易策略的适用情况,以便程序回测 短线核心:不参与任何级别的调整,采用龙空龙模式 昨日主题投资 连板进级率 6/39 15.3% 二进三: 进级率低 0% 最常用的二种方法: 方法…...
TCP 三次握手 四次挥手以及滑动窗口
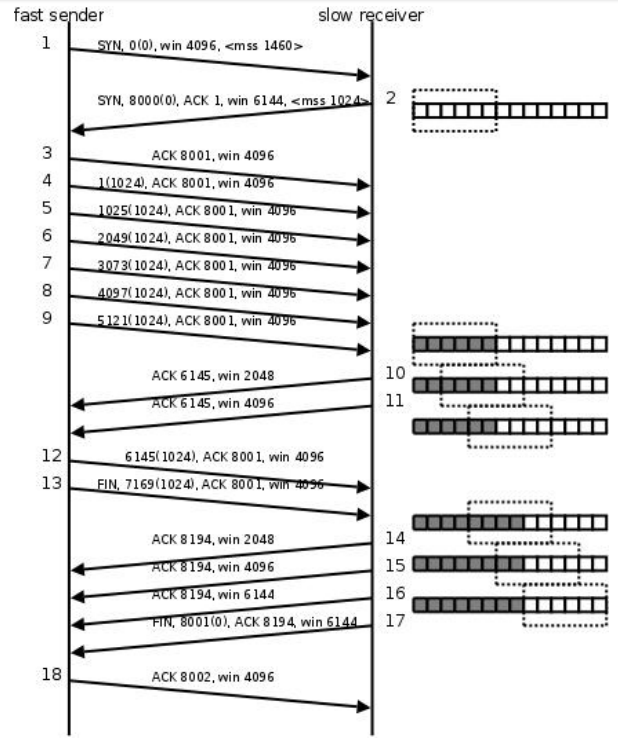
TCP 三次握手 简介: TCP 是一种面向连接的单播协议,在发送数据前,通信双方必须在彼此间建立一条连接。所谓的 “ 连接” ,其实是客户端和服务器的内存里保存的一份关于对方的信息,如 IP 地址、端口号等。 TCP 可以…...
yum指令——Linux的软件包管理器
. 个人主页:晓风飞 专栏:数据结构|Linux|C语言 路漫漫其修远兮,吾将上下而求索 文章目录 什么是软件包yum指令1.yum 是什么?2.Linux系统(Centos)的生态 3.yum的相关操作安装卸载yum的相关操作小结 软件源安…...

【WPF.NET开发】规划WPF应用程序性能
本文内容 对各种场景进行考虑定义目标了解平台使性能优化成为一个迭代过程构建图形丰富性 能否成功实现性能目标取决于如何制定性能策略。 规划是开发任何产品的第一阶段。 本主题介绍一些非常简单的规则,用于开发良好的性能策略。 1、对各种场景进行考虑 场景可…...

Ubuntu22.04报错:ValueError: the symlink /usr/bin/python3 does not point to ...
目录 一、背景 二、如何解决呢? 三、解决步骤 1. 确定可用的 Python 版本 2. 重新设置符号链接 3. 选择默认版本 4. 验证: 四、update-alternatives 详解 1. 命令语法 2. 常用选项 --install添加备选项。 --config:选择默认版本。 …...

什么是 React的refs?为什么它们很重要
Refs是React中的一个特殊属性,用于访问在组件中创建的DOM元素或组件实例。 Refs的重要性在于它们提供了一种直接访问DOM元素或组件实例的方式,使得我们可以在需要时操作它们。在某些情况下,例如在处理表单输入、媒体播放或触发动画等场景下&…...

使用yarn时--解决error Error: certificate has expired问题
【HTTPS 证书验证失败】导致的这个问题! 解决方案:将yarn配置中的 strict-ssl 设置为 flase , 在 info yarn config 信息中, strict-ssl 为 true,表示需要验证 HTTPS 证书。我们可以将 strict-ssl 设置为 false,跳过 H…...

Sql server强制走索引
遇到一个奇怪的问题,同样的SQL,只是一个where条件不一样,一个是column1 AAA,一个是column1 BBB,他们的查询效率却差距甚大,一个要60秒,一个1秒以下。查看查询计划,一个使用了索引&…...

解决Android Studio gradle下载超时和缓慢问题(win10)
解决超时问题 一般配置阿里云代理就可以解决。 具体配置方法,参考:https://blog.csdn.net/zhangjin1120/article/details/121739782 解决下载缓慢问题 直接去腾讯云镜像下载: https://mirrors.cloud.tencent.com/gradle/ 下载好了之后&…...

Ps:根据 HSB 调色(以可选颜色命令为例)
在数字色彩中,RGB 和 HSV(又称 HSB)是两种常用的颜色表示方式(颜色模型)。 在 RGB 颜色模式下,Photoshop 的红(Red)、绿(Green)、蓝(Blue…...

MySQL:事务隔离级别详解
事务一共有四个特性:原子性、隔离性、持久性、一致性。简称ACID。本文所将就是其中的隔离性。 1、事务中因为隔离原因导致的并发问题有哪些? 脏读:当事务A对一个数据进行修改,但这个操作还未提交,但此时事务B就已经读…...

golang 根据URL获取文件名
只有一个文件地址,但是没有文件名称,文件地址:http://XXXXXXX/getfile.aspx?fileid999 但是系统需要把文件名称也写入到数据库 可以根据 resp.Header["Content-Disposition"] 获取文件名 resp.Header["Content-Disposition&q…...
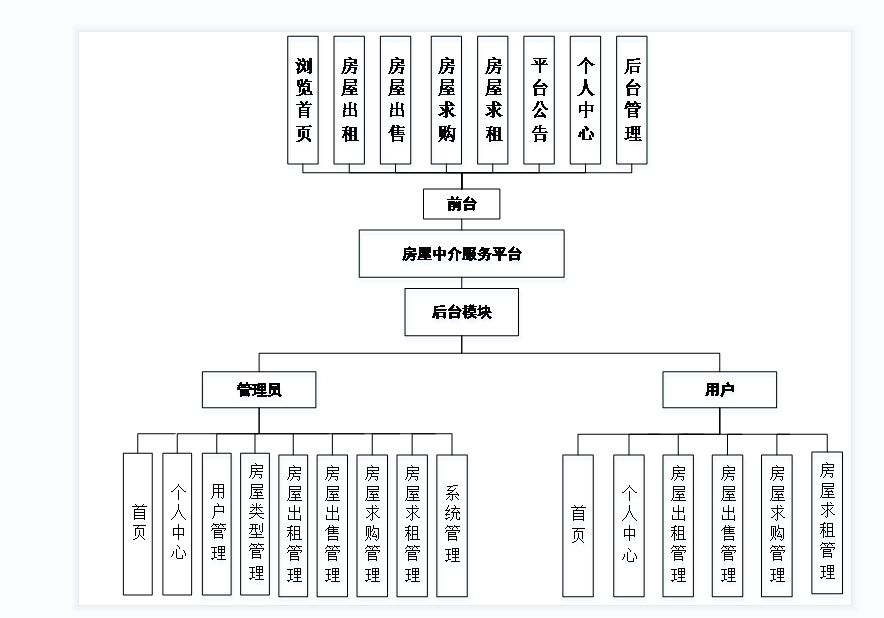
【Javaweb程序设计】【C00163】基于SSM房屋中介服务平台(论文+PPT)
基于SSM房屋中介服务平台(论文PPT) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于ssm的房屋中介服务平台 本系统分为前台、管理员、用户3个功能模块。 前台:当游客打开系统的网址后,首先看到的就是首页界面。…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
