Python中Numba库装饰器
一、运行速度是Python天生的短板
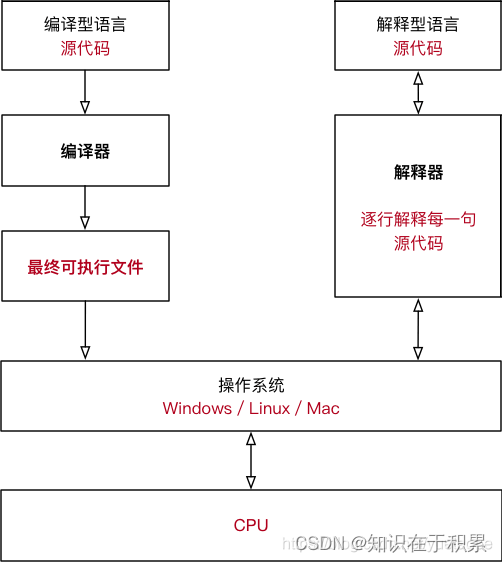
1.1 编译型语言:C++
对于编译型语言,开发完成以后需要将所有的源代码都转换成可执行程序,比如 Windows 下的.exe文件,可执行程序里面包含的就是机器码。只要我们拥有可执行程序,就可以随时运行,不用再重新编译了,也就是“一次编译,无限次运行”。
在运行的时候,我们只需要编译生成的可执行程序,不再需要源代码和编译器了,所以说编译型语言可以脱离开发环境运行。
编译型语言一般是不能跨平台的,也就是不能在不同的操作系统之间随意切换。
1.2 解释型语言:Python
对于解释型语言,每次执行程序都需要一边转换一边执行,用到哪些源代码就将哪些源代码转换成机器码,用不到的不进行任何处理。每次执行程序时可能使用不同的功能,这个时候需要转换的源代码也不一样。
因为每次执行程序都需要重新转换源代码,所以解释型语言的执行效率天生就低于编译型语言,甚至存在数量级的差距。计算机的一些底层功能,或者关键算法,一般都使用 C/C++ 实现,只有在应用层面(比如网站开发、批处理、小工具等)才会使用解释型语言。
在运行解释型语言的时候,我们始终都需要源代码和解释器,所以说它无法脱离开发环境。
1.3 速度对比:C++比Python快25倍
我不会C++语言、也没有C++语言的运行的环境,借用网友的对比结果:

编译后,运行C++代码,生成全部13-mers共6700万个大约需要2.42秒。这意味着运行相同算法,Python用时是C++的25倍多。
二、Numba使用与否的对比,计算1000万以内的素数
2.1 原生Python,计算1000万以内的素数
def U27_1000W以内的素数():import mathimport timedef is_prime(num):if num == 2:return Trueif num <= 1 or num % 2 == 0:return Falsefor div in range(3, int(math.sqrt(num) + 1), 2):if num % div == 0:return Falsereturn Truedef run_program(N):total = 0for i in range(N):if is_prime(i):total += 1return total# if __name__ == "__main__":N = 10000000start = time.time()total = run_program(N)end = time.time()print(f"1000万以内所有的素数有 {total} 个")print(f"纯Python耗时: {end - start} 秒\b")return end - start2.2 Numba装饰器,计算1000万以内的素数
def U28_1000W以内的素数_Numba装饰器():import mathimport timefrom numba import njit, prange# @njit 相当于 @jit(nopython=True) @njitdef is_prime(num):if num == 2: # 2为素数return Trueif num <= 1 or num % 2 == 0: # 偶数中除了2都不是素数return Falsefor div in range(3, int(math.sqrt(num) + 1), 2):if num % div == 0:return Falsereturn True#使用Numba的prange来进行并发循环计算@njit(parallel = True)def run_program(N):total = 0#使用Numba提供的prange参数来进行并行计算for i in prange(N):if is_prime(i):total += 1return total# if __name__ == "__main__":N = 10000000start = time.time()total = run_program(N)end = time.time()print(f"1000万以内所有的素数有 {total} 个")print(f"Numba装饰器耗时: {end - start} 秒\b")return end - start2.3 实测速度:使用numba装饰器,速度提升 22.0 倍,逼近C++
t0 = U27_1000W以内的素数()
t1 = U28_1000W以内的素数_Numba装饰器()
print(f'使用numba装饰器,速度提升 {round(t0/t1, 0)} 倍')1000万以内所有的素数有 664579 个
纯Python耗时: 86.78110885620117 秒
1000万以内所有的素数有 664579 个
Numba装饰器耗时: 3.9410934448242188 秒
使用numba装饰器,速度提升 22.0 倍
三、素数算法
质数也就是大于1的整数中,除了1和它本身以外不能被其他整数整除的数,也叫素数。
# 算法一:针对输入的数字x,我们可以遍历从2到x-1这个区间中的数,如果x能被这个区间中任意一个数整除,那么它就不是质数。
def is_prime1(x):for i in range(2, x):if x % i == 0:return Falsereturn True# 算法二:对算法一的优化,事实上只需要遍历从2到√x即可。
def is_prime2(x):for i in range(2, int(x ** 0.5) + 1):if x % i == 0:return Falsereturn True# 算法三:偶数中除了2都不是质数,且奇数的因数也没有偶数,因此可以进一步优化。
def is_prime3(x):if x == 2:return Trueelif x % 2 == 0:return Falsefor i in range(3, int(x ** 0.5) + 1, 2):if x % i == 0:return Falsereturn True# 算法四:任何一个自然数,总可以表示成以下六种形式之一:6n,6n+1,6n+2,6n+3,6n+4,6n+5(n=0,1,2...)我们可以发现,除了2和3,只有形如6n+1和6n+5的数有可能是质数。且形如6n+1和6n+5的数如果不是质数,它们的因数也会含有形如6n+1或者6n+5的数,因此可以得到如下算法:
def is_prime4(x):if (x == 2) or (x == 3):return Trueif (x % 6 != 1) and (x % 6 != 5):return Falsefor i in range(5, int(x ** 0.5) + 1, 6):if (x % i == 0) or (x % (i + 2) == 0):return Falsereturn True四、Numba
4.1 官方文档
numba 是一款可以将 python 函数编译为机器代码的JIT编译器,经过 numba 编译的python 代码(仅限数组运算),其运行速度可以接近 C 或 FORTRAN 语言。
官方文档链接:http://numba.pydata.org/numba-doc/latest/index.html
相关文章:

Python中Numba库装饰器
一、运行速度是Python天生的短板 1.1 编译型语言:C 对于编译型语言,开发完成以后需要将所有的源代码都转换成可执行程序,比如 Windows 下的.exe文件,可执行程序里面包含的就是机器码。只要我们拥有可执行程序,就可以随…...
Spring Boot Aop 执行顺序
Spring Boot Aop 执行顺序 1. 概述 在 spring boot 项目中,使用 aop 增强,不仅可以很优雅地扩展功能,还可以让一写多用,避免写重复代码,例如:记录接口耗时,记录接口日志,接口权限&…...

100天精通鸿蒙从入门到跳槽——第16天:ArkTS条件渲染使用教程
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通Golang》 — Go语言学习之旅!《100天精通鸿蒙》 — 从Web/安卓到鸿蒙大师!100天…...

【Linux C | 进程】Linux 进程间通信的10种方式(1)
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...
橘子学Mybatis08之Mybatis关于一级缓存的使用和适配器设计模式
前面我们说了mybatis的缓存设计体系,这里我们来正式看一下这玩意到底是咋个用法。 首先我们是知道的,Mybatis中存在两级缓存。分别是一级缓存(会话级),和二级缓存(全局级)。 下面我们就来看看这两级缓存。 一、准备工作 1、准备数据库 在此之…...
看图说话:Git图谱解读
很多新加入公司的同学在使用Git各类客户端管理代码的过程中对于Git图谱解读不太理解,我们常用的Git客户端是SourceTree,配合P4Merge进行冲突解决基本可以满足日常工作大部分需要。不同的Git客户端工具对图谱展示会有些许差异,以下是SourceTre…...

linux新增用户,指定home目录和bash脚本且加入到sudoer列表
前言 近3年一直用自动化脚本,搞得连useradd命令都不会用了。哈哈。 今天还碰到一个问题,有个系统没有‘useradd’和‘passwd’命令,直接蒙了。当然直接用apt install就能安装,不然还得自己编译折腾一会。新建用户 useradd -d /h…...

经典目标检测YOLO系列(三)YOLOV3的复现(1)总体网络架构及前向处理过程
经典目标检测YOLO系列(三)YOLOV3的复现(1)总体网络架构及前向处理过程 和之前实现的YOLOv2一样,根据《YOLO目标检测》(ISBN:9787115627094)一书,在不脱离YOLOv3的大部分核心理念的前提下,重构一款较新的YOLOv3检测器,来对YOLOv3有…...
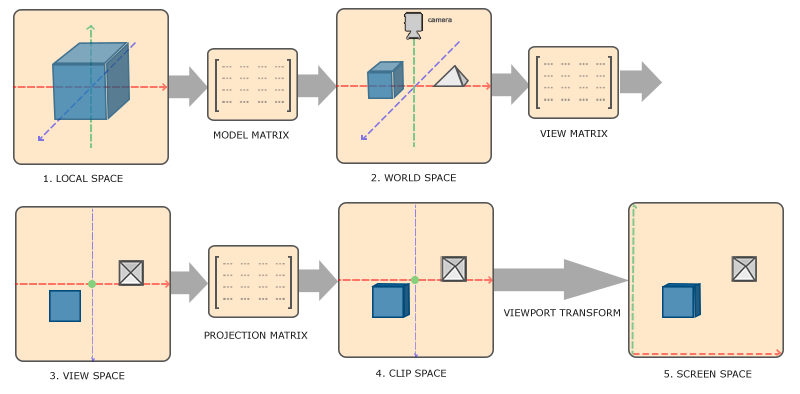
OpenGL/C++_学习笔记(四)空间概念与摄像头
汇总页 上一篇: OpenGL/C_学习笔记(三) 绘制第一个图形 OpenGL/C_学习笔记(四)空间概念与摄像头 空间概念与摄像头前置科技树: 线性代数空间概念流程简述各空间相关概念详述 空间概念与摄像头 前置科技树: 线性代数 矩阵/向量定…...

C语言2024-1-27练习记录
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>//int main() //{ // char c[15] { I, ,a,n,d, ,you,. }; // int i; // for(i 0; i < 15; i) //这个地方有几个地方需要注意一下,首先变量指定之后必须要加上英文状态下的分号 // printf("%c&q…...

深入解析HTTPS:安全机制全方位剖析
随着互联网的深入发展,网络传输中的数据安全性受到了前所未有的关注。HTTPS,作为HTTP的安全版本,为数据在客户端和服务器之间的传输提供了加密和身份验证,从而确保了数据的机密性、完整性和身份真实性。本文将详细探讨HTTPS背后的…...

【197】JAVA8调用阿里云对象存储API,保存图片并获取图片URL地址。
实际工作中,需要用阿里云对象存储保存图片,并且在上传图片到阿里云对象存储服务器后,获取图片在阿里云对象存储服务器的URL地址,以便给 WEB 前端显示。 阿里云对象存储上传图片的工具类 package zhangchao;import com.aliyun.os…...

2024.1.24 C++QT 作业
思维导图 练习题 1.提示并输入一个字符串,统计该字符中大写、小写字母个数、数字个数、空格个数以及其他字符个数 #include <iostream> #include <string.h> #include <array> using namespace std;int main() {string str;cout << "…...
jenkins部署过程记录
一、jenkins部署git链接找不到 原因分析: 机器的git环境不是个人git的权限,所以clone不了。Jenkins的master节点部署机器已经部署较多其他的job在跑,如果直接修改机器的git配置,很可能影响到其他的job clone 不了代码,…...

JS-策略设计模式
设计模式:针对特定问题提出的简洁优化的解决方案 一个问题有多种处理方案,而且处理方案随时可能增加或减少比如:商场满减活动 满50元减5元满100元减15元满200元减35元满500元减100元 // 满减金额计算函数 function count(money, type) {if …...

漏洞复现-EduSoho任意文件读取漏洞(附漏洞检测脚本)
免责声明 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直接或者间接的…...

「QT」QString类的详细说明
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C++」C/C++程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「...
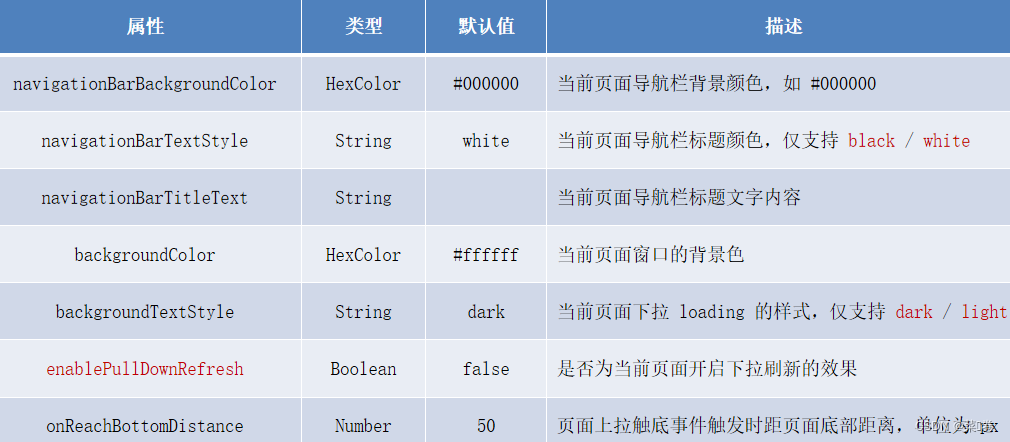
微信小程序-04
rpx(responsive pixel)是微信小程序独有的,用来解决屏适配的尺寸单位。 import 后跟需要导入的外联样式表的相对路径,用 ; 表示语句结束。 定义在 app.wxss 中的样式为全局样式,作用于每一个页面。 在页面的 .wxss 文…...
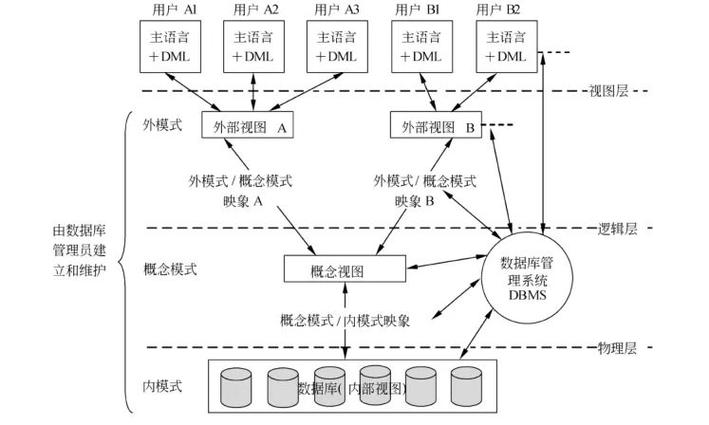
什么是数据库的三级模式两级映象?
三级模式两级映象结构图 概念 三级模式 内模式:也称为存储模式,是数据物理结构和存储方式的描述,是数据在数据库内部的表示方式。定义所有的内部记录类型、索引和文件组织方式,以及数据控制方面的细节。模式:又称概念…...

初识人工智能,一文读懂机器学习之逻辑回归知识文集(6)
🏆作者简介,普修罗双战士,一直追求不断学习和成长,在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验,历任核心研发工程师,项目技术负责人。 🎉欢迎 👍点赞✍评论…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
