二进制中1的个数
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO
联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬
学习必须往深处挖,挖的越深,基础越扎实!
阶段1、深入多线程
阶段2、深入多线程设计模式
阶段3、深入juc源码解析
阶段4、深入jdk其余源码解析
阶段5、深入jvm源码解析
码哥源码部分
码哥讲源码-原理源码篇【2024年最新大厂关于线程池使用的场景题】
码哥讲源码【炸雷啦!炸雷啦!黄光头他终于跑路啦!】
码哥讲源码-【jvm课程前置知识及c/c++调试环境搭建】
码哥讲源码-原理源码篇【揭秘join方法的唤醒本质上决定于jvm的底层析构函数】
码哥源码-原理源码篇【Doug Lea为什么要将成员变量赋值给局部变量后再操作?】
码哥讲源码【你水不是你的错,但是你胡说八道就是你不对了!】
码哥讲源码【谁再说Spring不支持多线程事务,你给我抽他!】
终结B站没人能讲清楚红黑树的历史,不服等你来踢馆!
打脸系列【020-3小时讲解MESI协议和volatile之间的关系,那些将x86下的验证结果当作最终结果的水货们请闭嘴】
题目描述
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
public int NumberOf1(int n) {if(n==0) {return 0;}int count=0;while(n!=0) {count++;n=n&(n-1);}return count;}
此解法是我在牛客网评论中看到的,确实是我所理解中最优的解法,下面我来分析一下此最优解法:
首先当二进制是0的时候直接返回0,这个毋庸置疑;
很多人第一眼看见会问代码里面没有考虑到负数的二进制情况(别急听我分析)
我们首先考虑正式,我们首先的情况所有的数不管是什么语言,其底层都是二进制编码,因为计算机只能读懂二进制.所以我们做题的时候根本不用考虑要不要将十进制转换成二进制的问题.
假设 n=22,那么它的二进制就是0001 0110 然后
进入循环-->
count=1,
n与(n-1)进行逻辑&运算-->0001 0110 & 0001 0101 -->0001 0100
(其实其本质就是从后面数1,数完一个1就把1拿掉,继续然后)
又进入循环-->
count=2,
n与(n-1)进行逻辑&运算-->0001 0100 & 0001 0011 -->0001 0000
又进入循环-->
count=3,
n与(n-1)进行逻辑&运算-->0001 0000 & 0000 1111 -->0000 0000
最后退出循环;
现在考虑负数,负数的话一共两步:
1.将负数先变成反码,
2.数它反码中1的个数,
第一步,操作系统已经帮我们做了,你觉得你还要干什么吗?
第二步,直接又是在二进制中数1的个数,不是一样的吗?难得正数的二进制和反码的二进制还有不同?
所以这题就这么简单的完美解决!
相关文章:

二进制中1的个数
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO 联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬 学习必须往深处挖&…...
)
python+matlab text(按图的相对位置显示)
python 用 python 画图时,如果想采用归一化的坐标来指定文本框的位置,则需要用到 transform ax.transAxes 参数,如 ax plt.gca() plt.text(0.1,0.2, "text", fontsize 20, transform ax.transAxes)matlab 方法1 text(___,Name…...

rust 引用/mut 的所有权
在任意给定时间,要么 只能有一个可变引用,要么 只能有多个不可变引用。 不可变引用(shared reference)实现了Copy trait,不会发生所有权转移可变引用(mutable reference)未实现,会发…...

油烟净化器科技改革,清新用餐生活
我最近分析了餐饮市场的油烟净化器等产品报告,解决了餐饮业厨房油腻的难题,更加方便了在餐饮业和商业场所有需求的小伙伴们。 随着餐饮业蓬勃发展,人们对用餐环境的要求也与日俱增。本文将深入研讨餐饮油烟净化器技术的改革方向,…...

[足式机器人]Part3 机构运动学与动力学分析与建模 Ch01-1 刚体系统的运动学约束
本文仅供学习使用,总结很多本现有讲述运动学或动力学书籍后的总结,从矢量的角度进行分析,方法比较传统,但更易理解,并且现有的看似抽象方法,两者本质上并无不同。 2024年底本人学位论文发表后方可摘抄 若有帮助请引用 本文参考: 《空间机构的分析与综合(上册)》-张启先…...

51单片机智能小车
51单片机智能小车 delay.c #include "intrins.h"void Delay2000ms() //11.0592MHz {unsigned char i, j, k;i 15;j 2;k 235;do{do{while (--k);} while (--j);} while (--i); }void Delay10us() //11.0592MHz {unsigned char i;i 2;while (--i); }void Delay…...

9. 嵌入式系统开发:安全性与可靠性设计模式---引言
在复杂的嵌入式系统设计中,为了提高嵌入式系统安全性并保护嵌入式系统免受各种潜在故障的影响,可以采用不同的设计模式。这些模式各自有优势和适用的场景: 1. 受保护的单通道模式(Protected Single Channel Pattern) …...
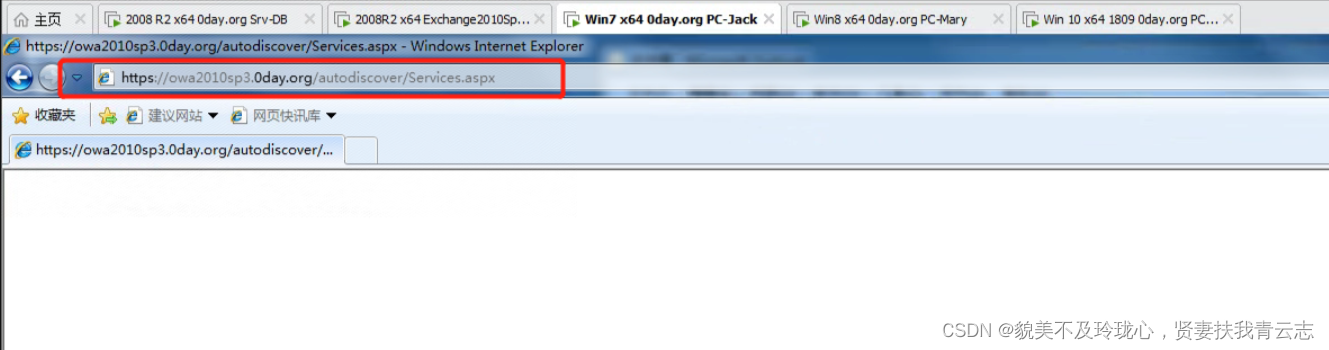
内网安全:Exchange服务
目录 Exchange服务 实验环境 域横向移动-内网服务-Exchange探针 一. 端口扫描 二. SPN扫描 三. 脚本探针(还可以探针是否有安全漏洞) 域横向移动-内网服务-Exchange爆破 一 .BurpSuite Intruder模块爆破 域横向移动-内网服务-Exchange漏洞 CVE-2020-17144 Exchange R…...

Flask介绍和优势
Flask诞生于2010年,是由Armin Ronacher用Python语言编写的一款轻量级Web开发框架。自发布以来,Flask逐渐成为开发人员喜爱的选择,并在2021年5月发布了Flask 2.0版本,引入了一些新增特性,如基本的异步支持。 使用Flask…...

喜报|「云原生数据库PolarDB」、「阿里云瑶池一站式数据管理平台」揽获“2023技术卓越奖”
日前,国内知名IT垂直媒体&技术社区IT168公布2023年“技术卓越奖”评选结果,经由行业CIO/CTO大咖、技术专家及IT媒体三方的联合严格评审,阿里云瑶池数据库揽获两项大奖:云原生数据库PolarDB荣获“2023年度技术卓越奖”…...

【动态规划】【字符串】【行程码】1531. 压缩字符串
作者推荐 视频算法专题 本文涉及知识点 动态规划汇总 LeetCode 1531. 压缩字符串 II 行程长度编码 是一种常用的字符串压缩方法,它将连续的相同字符(重复 2 次或更多次)替换为字符和表示字符计数的数字(行程长度)…...

检测头篇 | 原创自研 | YOLOv8 更换 SEResNeXtBottleneck 头 | 附详细结构图
左图:ResNet 的一个模块。右图:复杂度大致相同的 ResNeXt 模块,基数(cardinality)为32。图中的一层表示为(输入通道数,滤波器大小,输出通道数)。 1. 思路 ResNeXt是微软研究院在2017年发表的成果。它的设计灵感来自于经典的ResNet模型,但ResNeXt有个特别之处:它采用…...
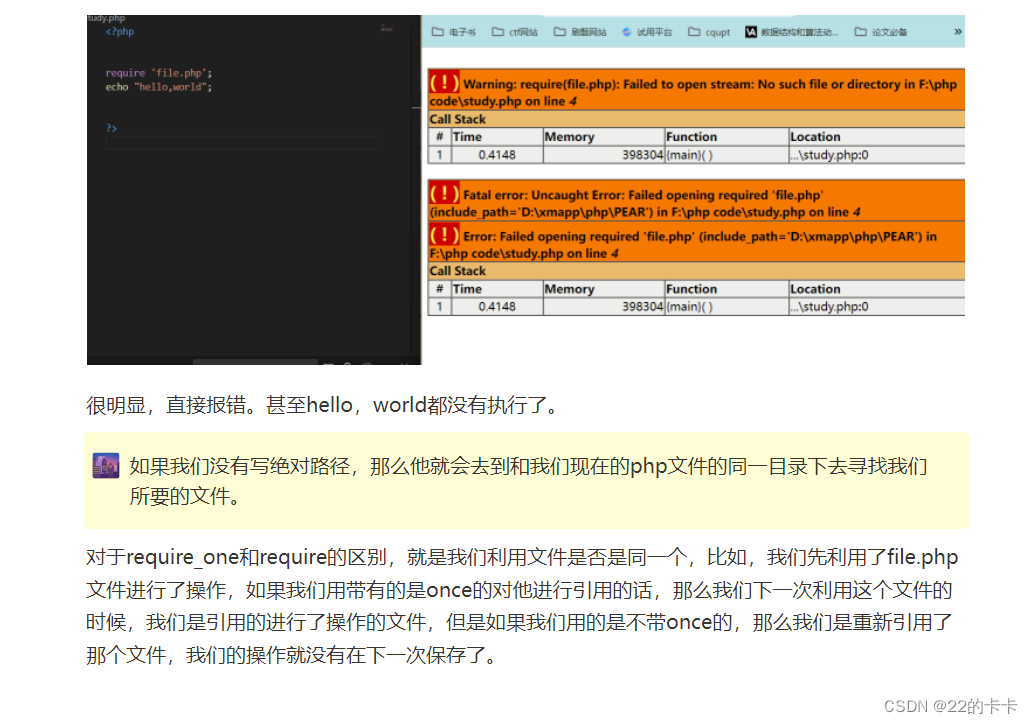
PHP语法
#本来是在学命令执行,所以学了学,后来发现,PHP语法和命令执行的关系好像没有那么大,不如直接学php的一些命令执行函数了。# #但是还是更一下,毕竟还是很多地方都要求掌握php作为脚本语言,所以就学了前面的…...
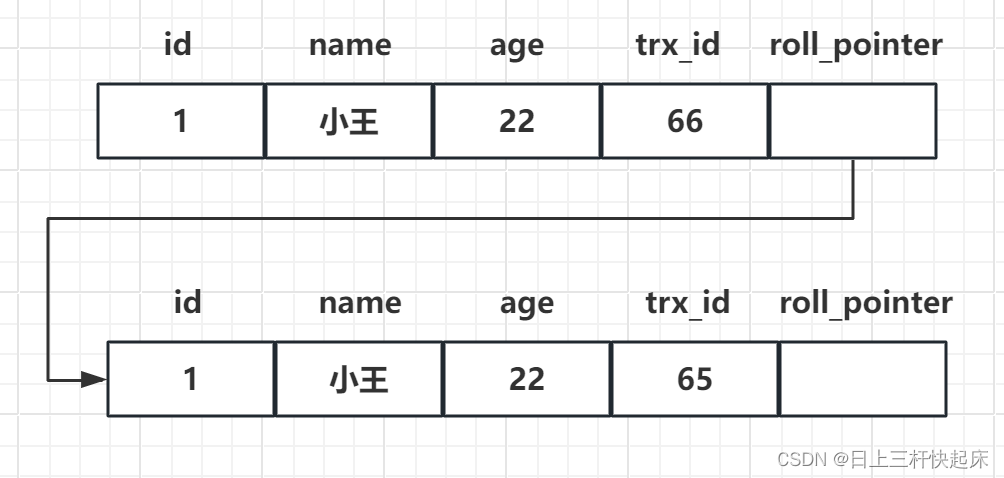
MySQL:三大日志(binlog、redolog、undolog)
再了解三个日志前我们先了解一下MySQL的两层架构: Server 层负责建立连接、分析和执行 SQL。MySQL 大多数的核心功能模块都在这实现,主要包括连接器,查询缓存、解析器、预处理器、优化器、执行器等。另外,所有的内置函数和所有跨…...

【QT+QGIS跨平台编译】之十二:【libpng+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文件目录 一、libpng介绍二、文件下载三、文件分析四、pro文件五、编译实践一、libpng介绍 PNG(Portable Network Graphics,便携式网络图形),是一种采用无损压缩算法的位图格式,支持索引、灰度、RGB三种颜色方案以及Alpha通道等特性。 PNG使用从LZ77派生的无损数据压缩算…...
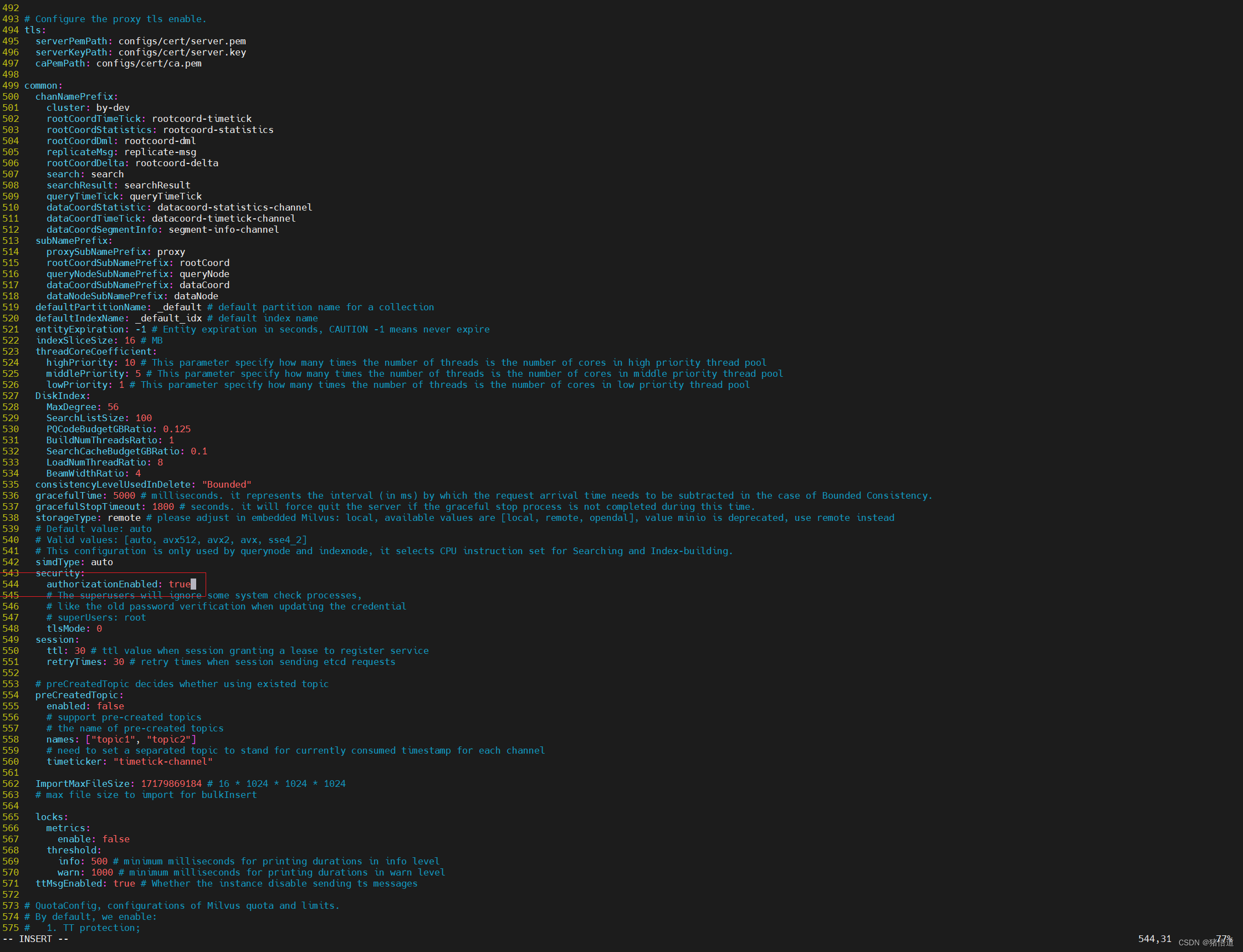
Windows 和 Anolis 通过 Docker 安装 Milvus 2.3.4
Windows 10 通过 Docker 安装 Milvus 2.3.4 一.Windows 安装 Docker二.Milvus 下载1.下载2.安装1.Windows 下安装(指定好Docker文件目录)2.Anolis下安装 三.数据库访问1.ATTU 客户端下载 一.Windows 安装 Docker Docker 下载 双击安装即可,安…...
)
JUC并发编程与源码分析学习笔记(三)
目录 五十六、JMM之入门简介 五十七、JMM之学术定义和作用 五十八、JMM之三大特性 五十九、JMM之多线程对变量的读写过程 六十、JMM之happens-before-上集 六十一、JMM之happens-before-下集 五十六、JMM之入门简介 Java内存模型之JMM 1、先从大厂面试题开始 ①、你知道…...
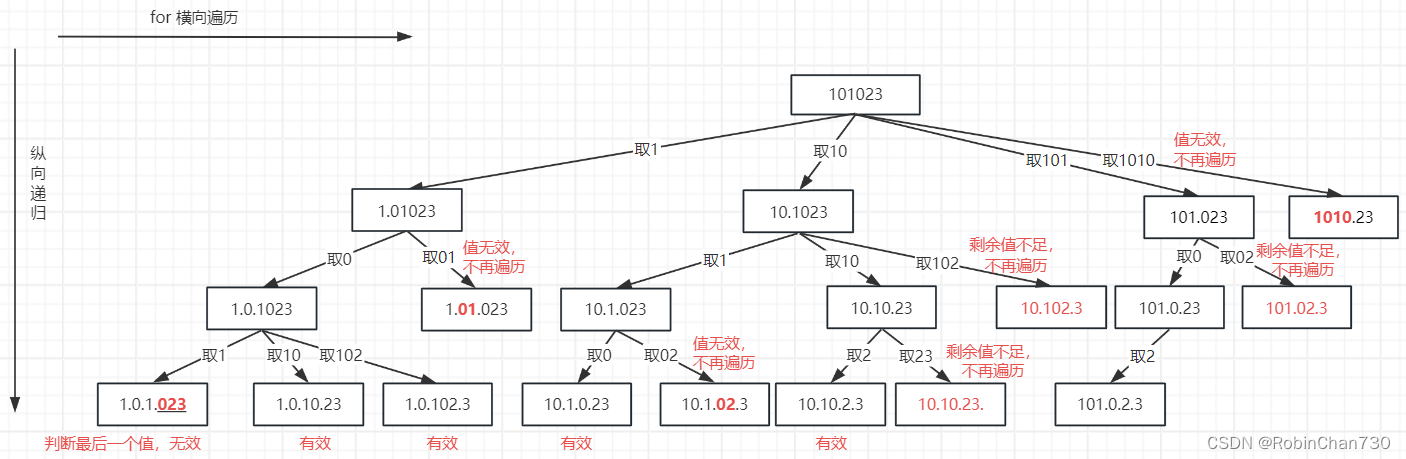
力扣日记1.28-【回溯算法篇】93. 复原 IP 地址
力扣日记:【回溯算法篇】93. 复原 IP 地址 日期:2023.1.28 参考:代码随想录、力扣 93. 复原 IP 地址 题目描述 难度:中等 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0&…...

Java 的反射学习总结
目录 一、什么是反射? 二、如何获取类对象? 三、如何通过类对象来创建类的对象? 四、类对象获取类构造器的方式 五、通过类对象获取类的属性 六、通过类对象获取类的方法 一、什么是反射? 反射是指在运行时动态地获取、检查…...

图论第二天|695. 岛屿的最大面积 1020. 飞地的数量 130. 被围绕的区域 417. 太平洋大西洋水流问题 827.最大人工岛
目录 Leetcode695. 岛屿的最大面积Leetcode1020. 飞地的数量Leetcode130. 被围绕的区域Leetcode417. 太平洋大西洋水流问题Leetcode827.最大人工岛 Leetcode695. 岛屿的最大面积 文章链接:代码随想录 题目链接:695. 岛屿的最大面积 思路:dfs …...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
