DAY_12(树链剖分)
中途摆烂了几天加上考试比赛啥的,导致目前写博客断了。。差了好几天的题目没学了qwq,现在还是按照每天学的东西来写博客吧
今天主要学了树链剖分,怎么说呢,虽然随便拿出今天写的一道题目来看,码量都是一两百行的,但是其实也不算太恶。。细说:
树链剖分有两种:重链剖分、长链剖分。前者特征是把“最大的”儿子成为重儿子,把树分为若干条重链;后者特征是把“最长链”称为长儿子,把树分为若干条长链。不过在应用中重链应用更多,故树链剖分一般默认为重链剖分。
重链剖分是提高树上搜索效率的一个高级方法。它按照一定规则,把树剖分成一条条线性的不相交的链,因此就将整棵树的操作转换成对链的操作,从而使操作的复杂度转为O(logn),转为从重链部。重链剖分的一个特性:每条链的DFS序是有序的,因此可以使用线段数处理,从而高效的解决一些树上的修改和查询问题。
首先我们来试试水——求lca
现在有两种方法求lca,它的各种算法都是通过快速的向上跳到祖先节点来实现的。
一、倍增法,用二进制递增直接向祖先跳;
二、数链剖分的跳法是:将树剖成从根到叶子的一条条链路,链路之间不相交,每条链上的任意两个相邻节点都是父子关系,每条链路内的节点可以看作一个集合,以链头为集,链路上的节点查询lca时都指向链头,从而实现快速跳。
下面我们来介绍几组概念:
1、size[x]:以x为根子树的大小(对于每个点,x儿子中size最大的作为他的重儿子,剩下的为轻儿子)
2、deep[x]:x的深度;
3、father[x]:x的父亲;
4、top[x]:指x所有在重链顶端;
5、重链:重边连接形成重边连接起来形成的链,每个点恰好属于一条重链;
6、轻边:连接x和x轻儿子的边;
预处理两遍DFS:
第一遍,算出deep[x],size[x],father[x],son[x]
第二遍:算出top[x](重儿子和父节点的链头相同)
lca(Lowest Common Ancestor),所谓LCA,是当给定一个有根树T时,对于任意两个结点u、v,找到一个离根最远的结点x,使得x同时是u和v的祖先,x 便是u、v的最近公共祖先
现在来一道题目:
P3379 【模板】最近公共祖先(LCA)
话不多说,直接上代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,m,s;
int x,y;
int depth[N];
int sizee[N];
int son[N];
int top[N];
int fath[N];
int head[N];
struct ee
{int to;int from;
}edge[N<<1];
int cnt;
void add(int u,int v)
{cnt++;edge[cnt].to=v;edge[cnt].from=head[u];head[u]=cnt;
}//链式前向星存图
void dfs1(int u,int fa)
{depth[u]=depth[fa]+1;//孩子树高=父亲树高+1 fath[u]=fa;//认父 sizee[u]=1;//初始化,u节点为本身 for(int i=head[u];i;i=edge[i].from){int v=edge[i].to;if(v!=fa){fath[v]=u;dfs1(v,u);sizee[u]+=sizee[v];if(!son[u]||sizee[son[u]]<sizee[v])son[u]=v;}}
}
void dfs2(int u,int topx)
{top[u]=topx;if(!son[u])return ;dfs2(son[u],topx);//重链优先 for(int i=head[u];i;i=edge[i].from){int v=edge[i].to;if(v!=fath[u]&&v!=son[u])dfs2(v,v);//轻链 }
}
int main()
{cin>>n>>m>>s;for(int i=1;i<n;i++){int u,v;cin>>u>>v;add(u,v);add(v,u);}dfs1(s,0);dfs2(s,s);for(int i=1;i<=m;i++){cin>>x>>y;while(top[x]!=top[y]){//x,y不在同一重链 if(depth[top[x]]<depth[top[y]])swap(x,y);//x成为更浅点 x=fath[top[x]];//跳跃 }if(depth[x]<=depth[y])cout<<x<<endl;elsecout<<y<<endl;}return 0;
}现在我们来写树链剖分
在数量剖分中,常常有如下几个应用:
1、修改某路径上各点的权值;
2、查询某路径上节点的权值之和;
3、修改以某点为根的子树上各点的权值;
4、查询以某点为根的树上所有节点的权值之和;
那么对于这样的模型,我们就自然而然会想到线段数,由于每条重链内部的节点是有序的,因此可以按DFS序将它们安排在一个线段树上,将每个重链看作一个连续的区间来对重链的内部进行修改和查询。
我们需要进行判断:
如果x和y在一条重链上,那么我们直接将X到Y这一条重链上各点权值累加,并且通过线段数进行修改
如果x和y很不幸不在同一条重点上,而在不同的子树,那么这时候我们需要通过x到lca(x,y)和y到lca(x,y)这两条链上的点的权值进行修改即可。
——但是我们在编程时,我们通常会在查询lca的同时,对所经过的节点直接进行修改——
查询x到y的路径上所有节点权值之和:同样的通过线段数进行查询,然后并进行相关操作即可。
对于以x为根节点的子树上各点权值的修改并查询:由于每棵子树上的所有节点的DFS序是连续的,也就是说每棵子树对应一个连续的区间,那么修改和查询子树与线段数对区间的修改和查询的操作就完全一致了。
题目:
P3384 【模板】重链剖分/树链剖分
代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
ll n,m,r,p;
ll com;
ll head[N];
ll x,y,z;
ll deep[N],siz[N],father[N],son[N];
ll top[N];
ll a[N];
ll newa[N];
ll id[N];
ll cou;
ll res;
struct ed
{ll to,from;
}edge[N<<1];
ll cnt;
struct tr
{ll lazy;ll num;
}tree[N<<2];
void add(ll u,ll v)
{cnt++;edge[cnt].to=v;edge[cnt].from=head[u];head[u]=cnt;
}
void dfs1(ll x,ll fa)
{deep[x]=deep[fa]+1;siz[x]=1;father[x]=fa;for(ll i=head[x];i;i=edge[i].from){ll v=edge[i].to;if(v!=fa){dfs1(v,x);siz[x]+=siz[v];if(!son[x]||siz[v]>siz[son[x]])son[x]=v;}}
}
void dfs2(ll x,ll topx)
{cou++;top[x]=topx;id[x]=cou;newa[cou]=a[x]%p;if(!son[x])return ;dfs2(son[x],topx);for(ll i=head[x];i;i=edge[i].from){ll v=edge[i].to;if(v!=father[x]&&v!=son[x])dfs2(v,v);}
}
//树链剖分
void build(ll rt,ll l,ll r)
{tree[rt].lazy=0;if(l==r){tree[rt].num=newa[l]%p;return ;}ll mid=(l+r)>>1;build(rt<<1,l,mid);build(rt<<1|1,mid+1,r);tree[rt].num=(tree[rt<<1].num%p+tree[rt<<1|1].num%p)%p;
}
void pushdown(ll rt,ll l,ll r)
{ll mid=(l+r)>>1;tree[rt<<1].lazy=(tree[rt<<1].lazy+tree[rt].lazy)%p;tree[rt<<1|1].lazy=(tree[rt<<1|1].lazy+tree[rt].lazy)%p;tree[rt<<1].num=(tree[rt<<1].num%p+tree[rt].lazy*(mid-l+1))%p;tree[rt<<1|1].num=(tree[rt<<1|1].num%p+tree[rt].lazy*(r-mid))%p;tree[rt].lazy=0;
}
void addplus(ll rt,ll l,ll r,ll L,ll R,ll k)
{if(L<=l&&r<=R){tree[rt].lazy+=k%p;tree[rt].num+=(k*(r-l+1))%p;return ;}if(tree[rt].lazy)pushdown(rt,l,r);ll mid=(l+r)>>1;if(L<=mid)addplus(rt<<1,l,mid,L,R,k);if(R>mid)addplus(rt<<1|1,mid+1,r,L,R,k);tree[rt].num=(tree[rt<<1].num%p+tree[rt<<1|1].num%p)%p;
}
void query(ll rt,ll l,ll r,ll L,ll R)
{if(l>=L&&r<=R){res+=tree[rt].num%p;return ;}if(tree[rt].lazy)pushdown(rt,l,r);ll mid=(l+r)>>1;if(L<=mid)query(rt<<1,l,mid,L,R);if(R>mid)query(rt<<1|1,mid+1,r,L,R);
}
//区间操作
void addrange(ll x,ll y,ll k)
{k%=p;while(top[x]!=top[y]){if(deep[top[x]]<deep[top[y]])swap(x,y);addplus(1,1,n,id[top[x]],id[x],k);x=father[top[x]];}if(deep[x]>deep[y])swap(x,y);addplus(1,1,n,id[x],id[y],k);
}
void queryrange(ll x,ll y)
{ll ans=0;while(top[x]!=top[y]){if(deep[top[x]]<deep[top[y]])swap(x,y);res=0;query(1,1,n,id[top[x]],id[x]);ans+=res%p;x=father[top[x]];}if(deep[x]>deep[y])swap(x,y);res=0;query(1,1,n,id[x],id[y]);ans+=res%p;cout<<ans%p<<endl;
}
//子树操作
void addsontree(ll x,ll k)
{addplus(1,1,n,id[x],id[x]+siz[x]-1,k);return ;
}
void querysontree(ll x)
{res=0;query(1,1,n,id[x],id[x]+siz[x]-1);cout<<res%p<<endl;
}
int main()
{cin>>n>>m>>r>>p;for(ll i=1;i<=n;i++)cin>>a[i];for(ll i=1;i<n;i++){ll u,v;cin>>u>>v;add(u,v);add(v,u);}dfs1(r,0);dfs2(r,r);build(1,1,n);for(ll i=1;i<=m;i++){cin>>com;if(com==1){cin>>x>>y>>z;addrange(x,y,z);}if(com==2){cin>>x>>y;queryrange(x,y);}if(com==3){cin>>x>>z;addsontree(x,z);}if(com==4){cin>>x;querysontree(x);}}return 0;
}P3258 [JLOI2014] 松鼠的新家
比上面模版居然简单多了。。。线段树其实用不着建。。。(害我debug好久)
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n;
int head[N];
int a[N],newa[N];
int id[N];
int father[N],deep[N],siz[N],son[N];
int top[N];
struct ee
{int to;int from;
}edge[N<<1];
int cnt;
int cou;
int res;
void add(int u,int v)
{cnt++;edge[cnt].to=v;edge[cnt].from=head[u];head[u]=cnt;
}
struct tr
{int lazy;int num;
}tree[N<<2];
void dfs1(int x,int fa)
{deep[x]=deep[fa]+1;father[x]=fa;siz[x]=1;for(int i=head[x];i;i=edge[i].from){int v=edge[i].to;if(v==fa)continue;dfs1(v,x);siz[x]+=siz[v];if(!son[x]||siz[son[x]]<siz[v])son[x]=v;}
}
void dfs2(int x,int topx)
{top[x]=topx;cou++;id[x]=cou;if(!son[x])return ;dfs2(son[x],topx);for(int i=head[x];i;i=edge[i].from){int v=edge[i].to;if(v!=son[x]&&v!=father[x])dfs2(v,v);}
}
void pushdown(int rt,int l,int r)
{int mid=(r+l)>>1;tree[rt<<1].lazy+=tree[rt].lazy;tree[rt<<1|1].lazy+=tree[rt].lazy;tree[rt<<1].num+=tree[rt].lazy*(mid-l+1);tree[rt<<1|1].num+=tree[rt].lazy*(r-mid);tree[rt].lazy=0;
}
void addplus(int rt,int l,int r,int L,int R,int k)
{if(l>=L&&r<=R){tree[rt].num+=k*(r-l+1);tree[rt].lazy+=k;return ;}if(tree[rt].lazy)pushdown(rt,l,r);int mid=(l+r)>>1;if(L<=mid)addplus(rt<<1,l,mid,L,R,k);if(R>mid)addplus(rt<<1|1,mid+1,r,L,R,k);tree[rt].num=tree[rt<<1].num+tree[rt<<1|1].num;
}
void query(int rt,int l,int r,int L,int R)
{if(l>=L&&r<=R){res+=tree[rt].num;return ;}if(tree[rt].lazy)pushdown(rt,l,r);int mid=(l+r)>>1;res=0;if(L<=mid)query(rt<<1,l,mid,L,R);if(R>mid)query(rt<<1|1,mid+1,r,L,R);
}
void addrange(int x,int y,int k)
{while(top[x]!=top[y]){if(deep[top[x]]<deep[top[y]])swap(x,y);addplus(1,1,n,id[top[x]],id[x],k);x=father[top[x]];}if(deep[x]>deep[y])swap(x,y);addplus(1,1,n,id[x],id[y],k);
}
void queryrange(int x)
{res=0;query(1,1,n,id[x],id[x]);cout<<res<<endl;
}
int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<n;i++) {int u,v;cin>>u>>v;add(u,v);add(v,u);}dfs1(1,0);dfs2(1,1);for(int i=1;i<=n-1;i++){addrange(a[i],a[i+1],1);addrange(a[i+1],a[i+1],-1);}for(int i=1;i<=n;i++)queryrange(i);return 0;
}相关文章:
)
DAY_12(树链剖分)
中途摆烂了几天加上考试比赛啥的,导致目前写博客断了。。差了好几天的题目没学了qwq,现在还是按照每天学的东西来写博客吧 今天主要学了树链剖分,怎么说呢,虽然随便拿出今天写的一道题目来看,码量都是一两百行的&…...
 | Column,Row - 线性布局)
Compose | UI组件(九) | Column,Row - 线性布局
文章目录 前言Column 的含义Column 的使用给 Column 加边框Column 使用 verticalArrangement 定位子项位置Column 使用 horizontalAlignment 定位子组件位置Column 设置了大小,可使用Modifier.align修饰符设置子组件对齐方式 Row 的含义Row 的使用 总结 前言 传统的…...
QT+VS实现Kmeans++
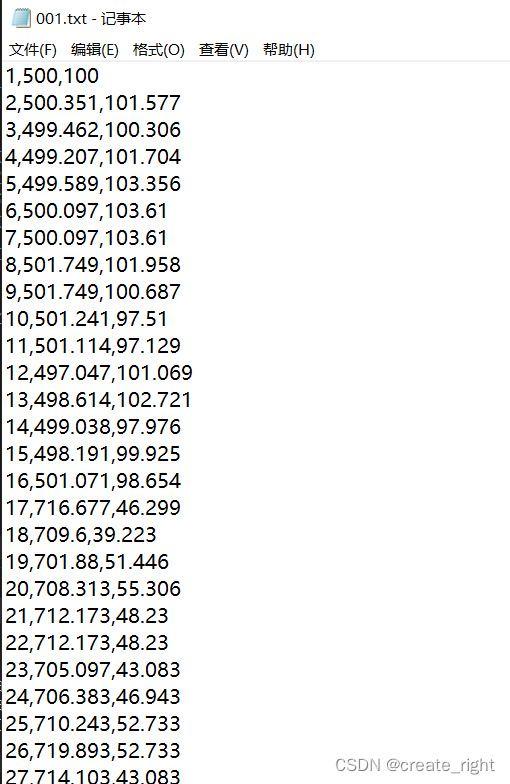
1、Kmeans的原理如下: (1)首先选取样本中任一数据点作为第一个聚类中心; (2)计算样本每一个数据点至现所有聚类中心的最近距离,并记录下来; (3)逐一挑选所…...

上位机图像处理和嵌入式模块部署(算法库的编写)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 作为图像处理的engineer来说,有时候我们需要提供上位机软件,有时候需要提供下位机程序,还有一种情况࿰…...

LeetCode1504. Count Submatrices With All Ones
文章目录 一、题目二、题解 一、题目 Given an m x n binary matrix mat, return the number of submatrices that have all ones. Example 1: Input: mat [[1,0,1],[1,1,0],[1,1,0]] Output: 13 Explanation: There are 6 rectangles of side 1x1. There are 2 rectangles…...
信息系统项目管理(第四版)(高级项目管理)考试重点整理第8章 项目整合管理(九))
(每日持续更新)信息系统项目管理(第四版)(高级项目管理)考试重点整理第8章 项目整合管理(九)
博主2023年11月通过了信息系统项目管理的考试,考试过程中发现考试的内容全部是教材中的内容,非常符合我学习的思路,因此博主想通过该平台把自己学习过程中的经验和教材博主认为重要的知识点分享给大家,希望更多的人能够通过考试&a…...

帕金森早期诊断准确率提高至 90.2%,深圳先进院联合中山一院提出 GSP-GCNs 模型
中山大学附属第一医院&中科大先进院等研究团队,提出了一种深度学习模型——图信号处理-图卷积网络 (GSP-GCNs),利用从涉及声调调节的特定任务中获得的事件相关脑电图数据来诊断帕金森病。 震颤、动作迟缓、表情僵硬……提起帕金森病,多数…...
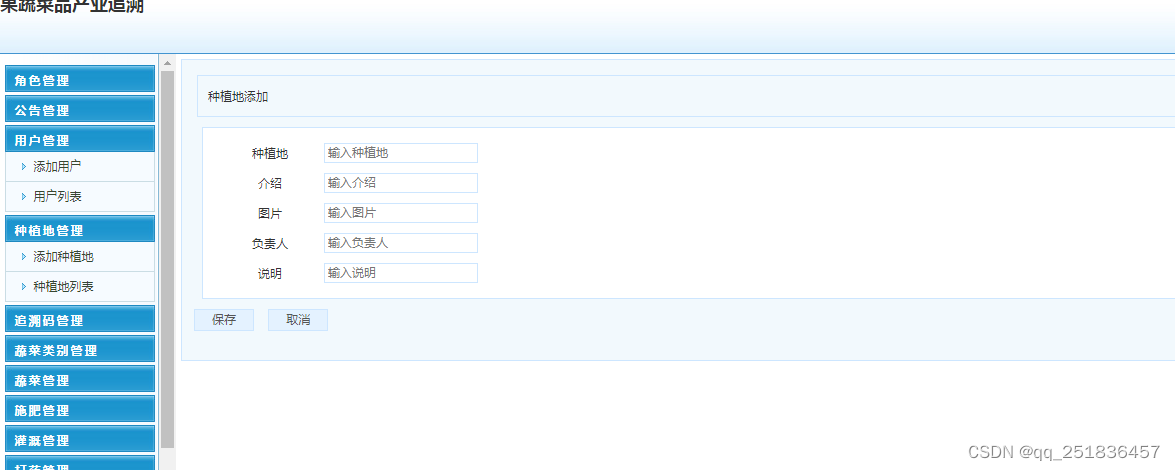
java servlet果蔬产业监管系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java Web果蔬产业监管系统是一套完善的java web信息管理系统 serlvetdaobean mvc 模式开发 ,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主 要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5…...
Flask 入门
1. 关于 Flask Flask诞生于2010年, Armin Ronacher的一个愚人节玩笑。不过现在已经是一个用python语言基于Werkzeug工具箱编写的轻量级web开发框架,它主要面向需求简单,项目周期短的小应用。 Flask本身相当于一个内核,其他几乎所…...

微信小程序Skyline在手机端不渲染的问题之一及其解决方式
问题:电脑端是skyline渲染,手机端是webview渲染?如何解? 开发者工具 当前渲染模式:Skyline 当进行预览时手机端却是: 请注意看轮播图的显示情况 请注意看轮播图的显示情况 请注意看轮播图的显示情况 从轮播图上来看,手机端是webview渲染…...

怎样做好Code Review
Code Review方案 定义 Code Review代码评审是指在软件开发过程中,通过对源代码进行系统性检查的过程。通常的目的是查找各种缺陷,包括代码缺陷、功能实现问题、编码合理性、性能优化等;保证软件总体质量和提高开发者自身水平 code review …...

臻于至善,CodeArts Snap 二维绘图来一套不?
前言 我在体验 华为云的 CodeArts Snap 时,第一个例子就是绘制三角函数图像,功能注释写的也很简单。 业务场景中,有一类就是需要产出各种二维图形的,比如,折线图、散点图、柱状图等。 为了提前积累业务素材…...

STM32学习笔记(二) —— 调试串口
我们在调试程序时,经常会使用串口打印相关的调试信息,但是单片机串口不能直接与 PC 端的 USB 接口通讯,需要用到一个USB转串口的芯片来充当翻译的角色。我们使用的开发板上有这个芯片,所以在打印调试信息的时候直接使用USB线连接开…...

Ubuntu20.0.4下设置frpc开机自启动
目录 一、下载frp 二、解压 三、服务端部署 1.配置 2.运行 三、客户端部署 1、配置 2、后台运行 四、开机启动 1、拷贝frpc.service 2、修改配置 3、启用服务 五、ubuntu20.04使用 rc-local.service设置开机启动 1、建立开机服务添加 [Install] 段 2、授权rc-local.service 3、…...
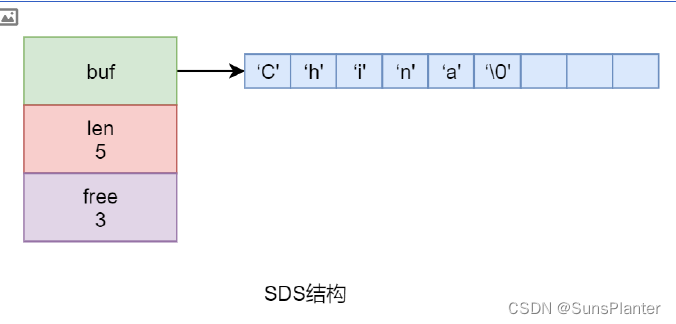
05 Redis之Benchmark+简单动态字符串SDS+集合的底层实现
3.8 Benchmark Redis安装完毕后会自动安装一个redis-benchmark测试工具,其是一个压力测试工具,用于测试 Redis 的性能。 src目录下可找到该工具 通过 redis-benchmark –help 命令可以查看到其用法 3.8.1 测试1 3.9 简单动态字符串SDS 无论是 Redis …...

【C++】priority_queue优先队列
头文件#include <queue> 优先队列具有队列的所有特性,本质是一个堆实现的,和队列基本操作相同: top 访问队头元素 empty 队列是否为空 size 返回队列内元素个数 push 插入元素到队尾 (并排序) emplace 原地构造一个元素并插入队列 pop 弹出队头元素…...

蓝桥杯---三国游戏
问题描述 小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵 X, Y, Z (一开始可以认为都为 0 )。游戏有 n 个可能会发生的事件,每个事件之 间相互独立且最多只会发生一次,当第 i 个事件发生时会分别让 X, Y, Z 增加 Ai , Bi ,Ci 。…...

设计一个分布式ID
为了保证全局唯一性可以用时间作为区分点一部分,时间尽可能细化,可以精确到毫秒,甚至是微秒和纳秒。如果是分布式系统有多态机器,可以根据机器ID再进行以下区分。如哦机器运行的特别快,1毫秒有大量ID生成,可…...

259:vue+openlayers: 显示海量多边形数据,10ms加载完成
第259个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+openlayers项目中通过WebGLVectorLayerRenderer方式加载海量多边形数据。这里相当于将海量的数据放在同一个层的source中,然后通过webglTile的方式渲染出这一层。 本示例数据为5000个多边形,加载速度超级快。 直接…...

Go Zero微服务个人探究之路(十)实战走通微服务前台请求调用的一套流程model->rpc微服务->apiHTTP调用
前言 Go语言凭借低占用,高并发等优秀特性成为后台编程语言的新星,GoZero框架由七牛云技术副总裁团队编写,目前已经成为Go微服务框架里star数量最多的框架 本文记录讲述笔者一步步走通前台向后台发出请求,后台api调用rpc服务的相…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...
