LeetCode 剑指 Offer II 083. 没有重复元素集合的全排列
给定一个不含重复数字的整数数组 nums ,返回其 所有可能的全排列 。可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
解法一:直接使用STL:
class Solution {
public:vector<vector<int>> permute(vector<int>& nums) {// next_permutation函数每次产生下一个排列// 下一个排列的含义是按字典顺序下一个更大的排列// 因此需要先对nums进行从小到大排序sort(nums.begin(), nums.end());vector<vector<int>> ans;do {ans.push_back(nums);} while (next_permutation(nums.begin(), nums.end()));return ans;}
};
如果输入数组大小为n,此算法时间复杂度为O(n*n!),空间复杂度为O(1)。next_permutation函数的时间复杂度最多为O(n)。
解法二:回溯法,遍历某个排列的每一个元素,当遍历到下标i时,我们遍历所有可以放到下标i的元素,但有些元素在前面已经用过了,因此我们维护一个visited数组,如果该元素没有用过,才放到下标i:
class Solution {
public:vector<vector<int>> permute(vector<int>& nums) {vector<vector<int>> ans;unordered_set<int> visited;vector<int> current;backtrack(0, current, nums, visited, ans);return ans;}private:void backtrack(int pos, vector<int> current, vector<int> &nums, unordered_set<int> &visited, vector<vector<int>> &ans) {int sz = nums.size();if (pos == sz) {ans.push_back(current);}for (int i = 0; i < sz; ++i) {if (visited.find(nums[i]) != visited.end()) {continue;}visited.insert(nums[i]);current.push_back(nums[i]);backtrack(pos + 1, current, nums, visited, ans);current.pop_back();visited.erase(nums[i]);}}
};
如果输入数组大小为n,此算法时间复杂度为O(n*n!),空间复杂度为O(n)。backtrack函数的调用次数为O(n!),每次调用中,会循环n次。对于空间复杂度,递归深度为n,主要开销是栈空间开销和current、visited数组开销。
解法三:在解法二中,我们使用了visited数组来标记哪些元素已经被全排列过了,我们可以直接修改nums数组,当遍历到下标i时,我们可以令[0,i]的所有元素都是已经全排列过的元素,具体做法是将当前循环中要排列的元素和下标为i的元素交换:
class Solution {
public:vector<vector<int>> permute(vector<int>& nums) {vector<vector<int>> ans;backtrack(0, nums, ans);return ans;}private:void backtrack(int pos, vector<int> &nums, vector<vector<int>> &ans) {int sz = nums.size();if (pos == sz) {ans.push_back(nums);}for (int i = pos; i < sz; ++i) {swap(nums[i], nums[pos]);backtrack(pos + 1, nums, ans);swap(nums[i], nums[pos]);}}
};
如果输入数组大小为n,此算法时间复杂度为O(n*n!),空间复杂度为O(n)。backtrack函数的调用次数为O(n!),每次调用中,会循环n次。对于空间复杂度,递归深度为n,主要开销是栈空间开销。
相关文章:

LeetCode 剑指 Offer II 083. 没有重复元素集合的全排列
给定一个不含重复数字的整数数组 nums ,返回其 所有可能的全排列 。可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 1 < nums.length < 6 -10 < nu…...

JSONObject与JSONArray使用区别
目录 1.使用的场景区别 2. 使用方法区别 3.获取方式不同 4. 解析JSON字符串 5.总结 1.使用的场景区别 想通过键值对的形式获取数据,使用JSONObject。如果后台查询的是某个bean的list集合向前端页面传递,使用JSONArray。 2. 使用方法区别 创建方法不…...

经典C程序例程:通过进程ID得到文件名
通过进程ID得到文件名 #include <stdio.h> #include <windows.h> #include <tlhelp32.h> #include <tchar.h>BOOL EnablePrivilege(HANDLE hToken,LPCSTR szPrivName); void DispProcess(void); void DispPrsFile(void);// typedef BOOL (_stdcall *E…...
【Java】Spring MVC程序开发
文章目录Spring MVC程序开发1. 什么是Spring MVC?1.1 MVC定义1.2 MVC 和 Spring MVC 的关系2. 为什么学习Spring MVC?3. 怎么学习Spring MVC?3.1 Spring MVC的创建和连接3.1.1 创建Spring MVC项目3.1.2 RequestMapping 注解介绍3.1.3 Request…...

leetcode题解-704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nums [-1,0,3,5,9,12], target 9 输出: 4 解释: 9 出现…...

2.2 C语言程序的错误条件
在C语言程序中,条件语句决定程序的执行路径,因此条件表达式是程序的关键。 应用最经典的程序,除法的减法实现程序,解释条件表达式的重要性。x=y*q+r,x是被除数,y是除数,q是商,r是余数。 程序的方法, x=(r-y)+y*(1+q)。 main(){ /*错误条件的程序*/ r:=x; q:=0; whil…...
laravel 邮件发送
配置 Laravel 的邮件服务可以通过 config/mail.php 配置文件进行配置。 邮件中的每一项都在配置文件中有单独的配置项,甚至是独有的「传输方式」,允许你的应用使用不同的邮件服务发送邮件 mailers > [smtp > [transport > smtp,host > env(M…...

高性能 Jsonpath 框架,Snack3 3.2.57 发布
Snack3,一个高性能的 JsonPath 框架 借鉴了 Javascript 所有变量由 var 申明,及 Xml dom 一切都是 Node 的设计。其下一切数据都以ONode表示,ONode也即 One node 之意,代表任何类型,也可以转换为任何类型。 强调文档…...
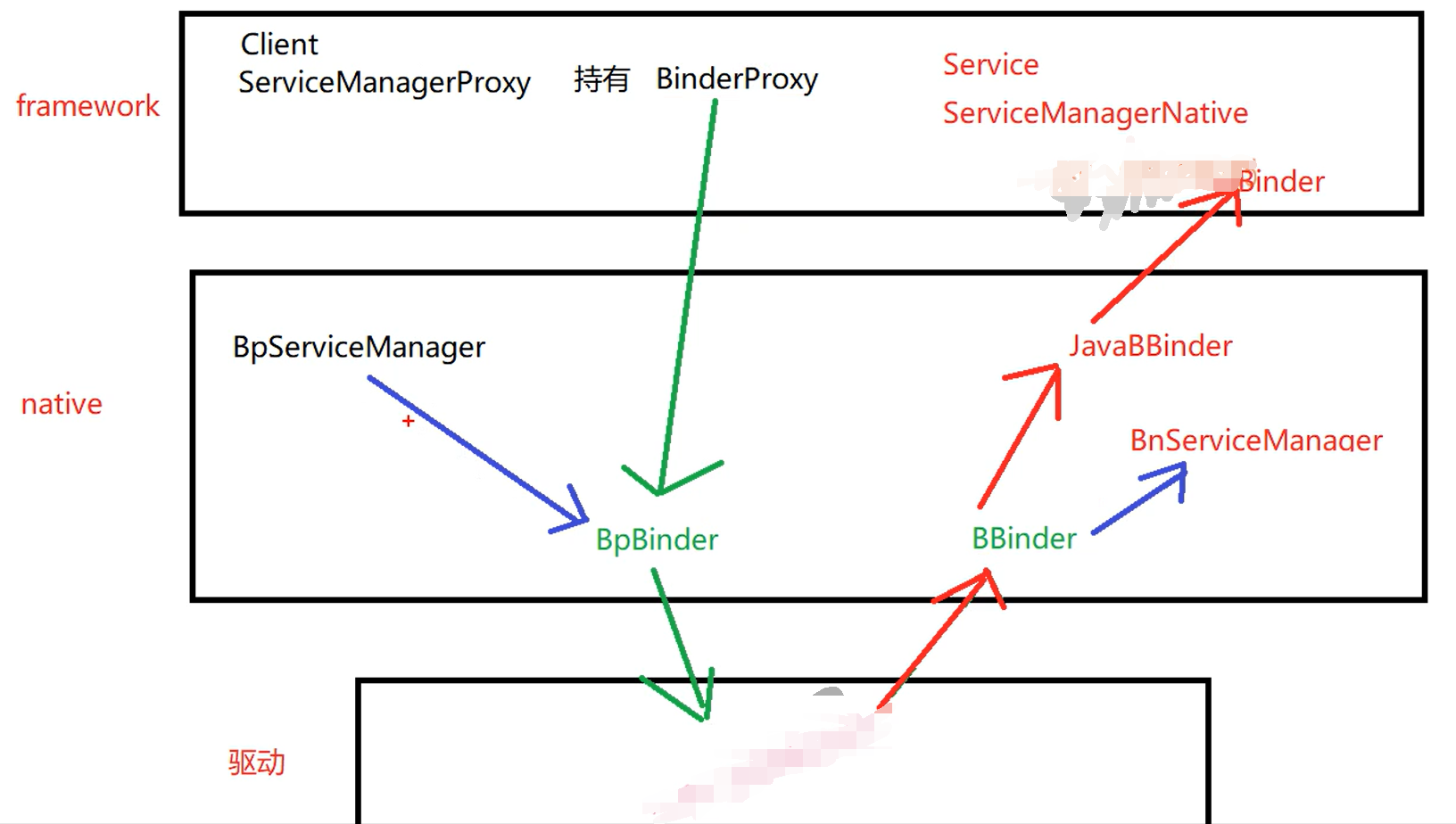
Android---进程间通信机制3
1 服务如何注册到 SM 中 getIServiceManager().addService(name, service, false); getIServiceManger --- new ServiceManagerProxy(new BinderProxy()) BinderInternal.getContextObject --- 返回 BinderProxy 对象 ProcessState::self()->getContextObject: 创建一个 BpB…...

Python实战,爬取金融期货数据
大家好,我是毕加锁。 今天给大家带来的是 Python实战,爬取金融期货数据 文末送书! 文末送书! 文末送书! 任务简介 首先,客户原需求是获取https://hq.smm.cn/copper网站上的价格数据(注:获取的是…...
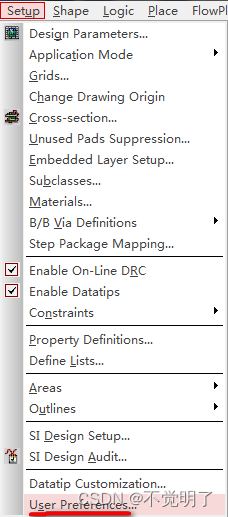
Allegro如何导入第三方网表操作指导
Allegro如何导入第三方网表操作指导 在用Allegro做PCB设计的时候,除了支持第一方网表的导入,同样也是可以导入第三方网表的,第三方网表如下图 如何导入,具体操作如下 点击Setup点击User Preference...
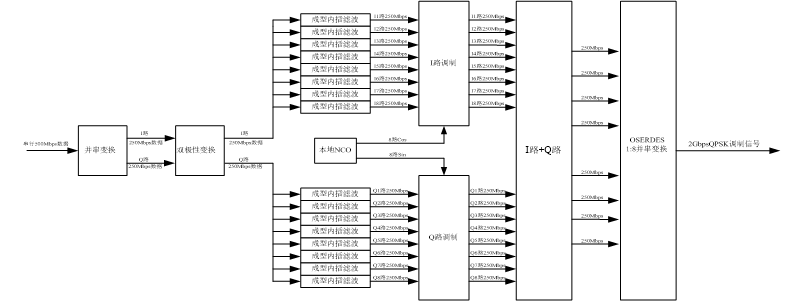
高码率QPSK调制解调方案(FPGA实现篇)
在前面的章节中,已经讲过QPSK调制的方案和Matlab算法仿真,在本篇中,主要讲解基于FPGA的高速QPSK调制的实现。根据前面提到的技术指标,本系统传输的数据速率为500Mbps,中频为720MHz,因此,传统的串行QPSK调制已经不合适在FPGA中实现,需采用全数字的并行方式进行调制,具体…...

Elasticsearch的RESTful Api使用
Elasticsearch的RESTful Api使用 文章目录Elasticsearch的RESTful Api使用查询集群健康情况查看所有索引其他的_cat命令创建索引删除索引修改索引查看索引创建文档批量操作文档删除文档查询文档全量更新文档局部更新文档索引的搜索分词分析分数说明查询类型分析查询集群健康情况…...

软著申请需要注意的
一、文档格式 (1)程序源代码和说明文档,源码前后30页,文档前后30页。 (2)软件源代码和说明书的页眉必须标明软件名称、版本号和页码,应当与申请表中相应内容完全一致 (3)…...

SpringBoot入门 - 添加Logback日志
SpringBoot开发中如何选用日志框架呢? 出于性能等原因,Logback 目前是springboot应用日志的标配; 当然有时候在生产环境中也会考虑和三方中间件采用统一处理方式。日志框架的基础在学习这块时需要一些日志框架的发展和基础,同时了…...

社会实践报告
中文摘要: 注重素质教育的今天,社会实践活动一直被视为高校培养德、智、体、美、劳全面发展的跨 世纪优秀人才的重要途径。团期社会实践活动是学校教育向课堂外的一种延伸,也是推进素质教育进程的重 手段。它有助于当代大学生接触社会,了解社…...

LeetCode 460. LFU 缓存 -- 哈希查询+双向链表
LFU 缓存 困难 634 相关企业 请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。 实现 LFUCache 类: LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象 int get(int key) - 如果键 key 存在于缓存中,则获取键…...

Dubbo 源码分析 – SPI 机制
1.简介 SPI 全称为 Service Provider Interface,是一种服务发现机制。SPI 的本质是将接口实现类的全限定名配置在文件中,并由服务加载器读取配置文件,加载实现类。这样可以在运行时,动态为接口 加载实现类。正因此特性࿰…...
JDBC概述二(JDBC编程+案例展示)
一(JDBC的编程步骤) 1.加载数据库驱动 加载数据库驱动通常使用class类的静态方法forName()来实现,具体实现方式如下: Class.forName(“DriverName”),DriverName就是数…...

广度和深度优先搜索解析与示例代码
一,什么是搜索算法 算法是基于特定数据结构之上的,深度优先搜索算法和广度优先搜索算法都是基于“图”这种数据结构的。 树是图的一种特例(连通无环的图就是树)。 图上的搜索算法,最直接的理解就是,在图中找出从一个顶点出发,到另一个顶点的路径。具体方法有很多,两种…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
