堆和堆排序【数据结构】
目录
- 一、堆
- 1. 堆的存储定义
- 2. 初始化堆
- 3. 销毁堆
- 4. 堆的插入
- 向上调整算法
- 5. 堆的删除
- 向下调整算法
- 6. 获取堆顶数据
- 7. 获取堆的数据个数
- 8. 堆的判空
- 二、Gif演示
- 三、 堆排序
- 1. 堆排序
- (1) 建大堆
- (2) 排序
- 2.Topk问题
- 四、完整代码
- 1.堆的代码
- Heap.c
- Heap.h
- test.c
- 2. 堆排序的代码
前言:
什么是堆呢?
堆(Heap)是一种数据结构,它是 一种特殊的二叉树 ,其中父节点的键值总是大于或等于(或小于或等于)其任何一个子节点的键值。这意味着在堆中,根节点具有最大(或最小)键值。
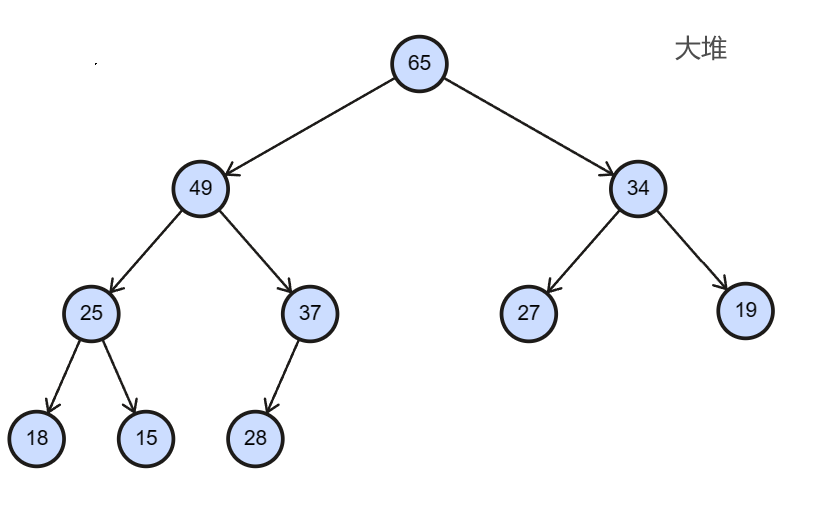
堆:一般是数组数据看做一棵完全二叉树
完全二叉树的逻辑结构:
-
大堆: 任意一个父结点 大于等于 子结点

-
小堆: 任意一个父结点 小于等于 子结点

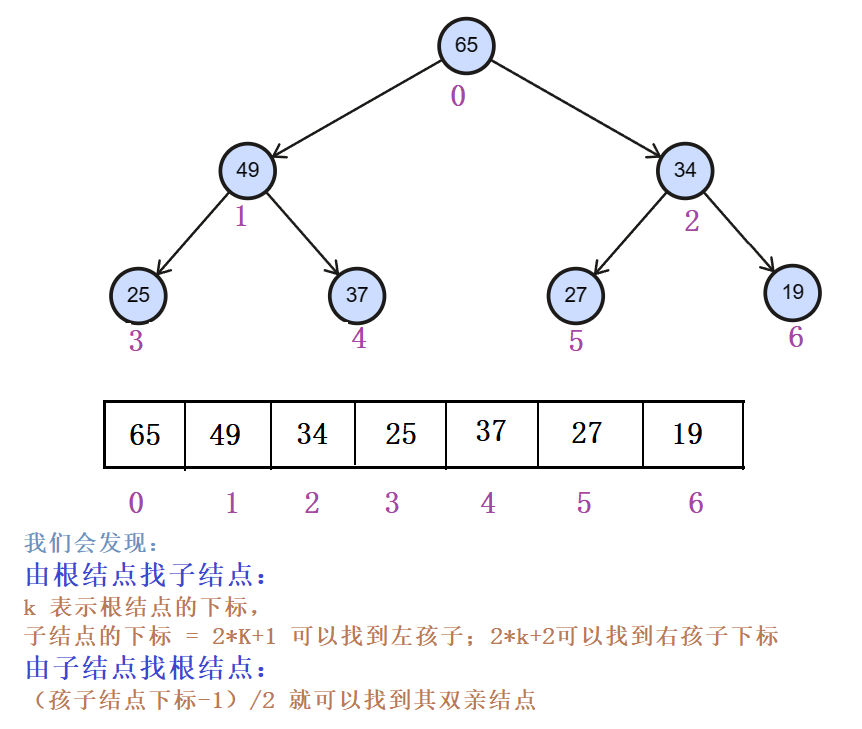
数组存储完全二叉树
一、堆
1. 堆的存储定义
因为存储结构,这里使用动态数组的形式来存放数据。但是也要注意其中的逻辑结构是完全二叉树。定义一个指针指向动态数组,定义存储堆的容量capacity,记录堆中的数据的个数size
代码
typedef int HPDataType;
typedef struct Heap
{HPDataType* a; //指向动态数组int capacity; //堆的容量int size; //堆中数据个数
}Heap;
2. 初始化堆
类似顺序表的初始化
代码
//初始化堆
void InitHeap(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}
3. 销毁堆
避免内存泄漏
代码
//销毁堆
void DestroyHeap(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = hp->size = 0;
}
4. 堆的插入
重点:
在堆的插入前,我们需要注意的就是,首先判断其容量,然后使用realloc给数组分配空间
分配空间后,把数据插入堆。但是数据在插入堆时,由于堆一般分为大根堆和小根堆,所以这里使用的大根堆。 大堆:父结点的值大于等于其孩子结点的值
但是数据的值不能确定,这个时候就需要我们使用 堆的向上调整算法
向上调整算法
在数组的末端插入元素,进行与其父结点进行比较,大堆的情况下,如果其孩子结点的值大于父亲结点的值时,把插入的数据向上调整,向上调整的方法是:把插入的数据与其父结点进行交换,交换后继续判断是否还需要向上调整。(使用向上调整算法的条件是前面结点的树是构成堆的)
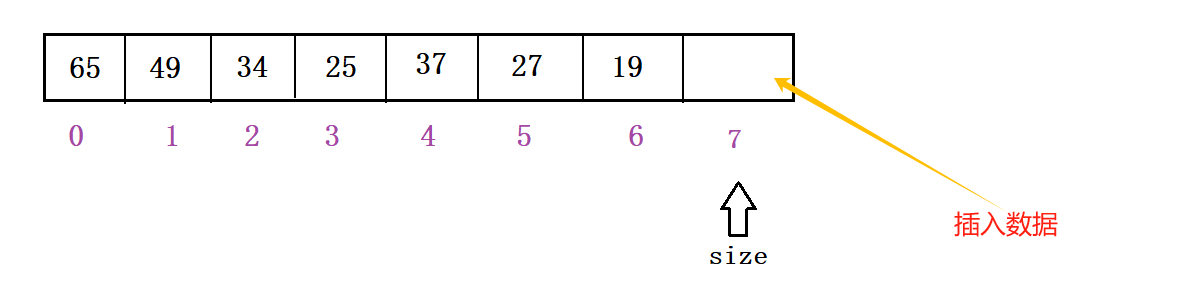
这里是使用的是数组,所以当插入元素时,在数组的末端进行插入数据
物理存储:
逻辑存储情况:
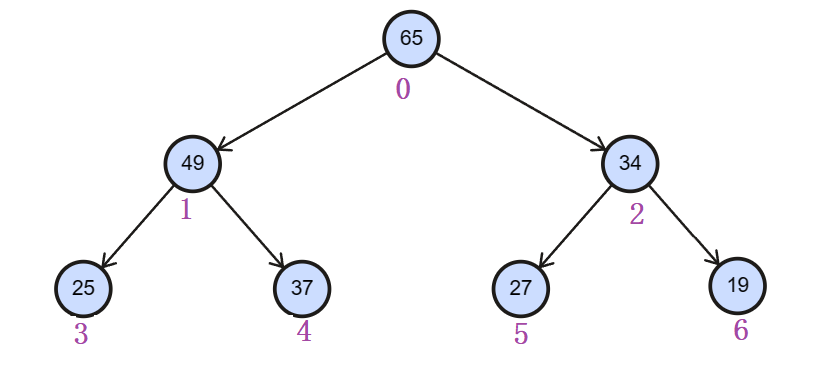
在插入的数据时,我们就需要考虑一下,
1. 当插入的孩子结点的值大于其父亲结点的值时,就向上调整
思路:
首先是根据孩子结的下标找父结点的下标,(孩子结点下标-1)/2 == 父结点下标,因为可能调整所以将判断条件放到循环里面(当然也可以用递归),在循环里面切记一定要及时更新当前孩子结点的下标和父结点的下标,孩子结点的值大于父结点的值就向上调整,否则就跳出循环。当孩子结点的下标到0时,向上调整完成,循环结束。
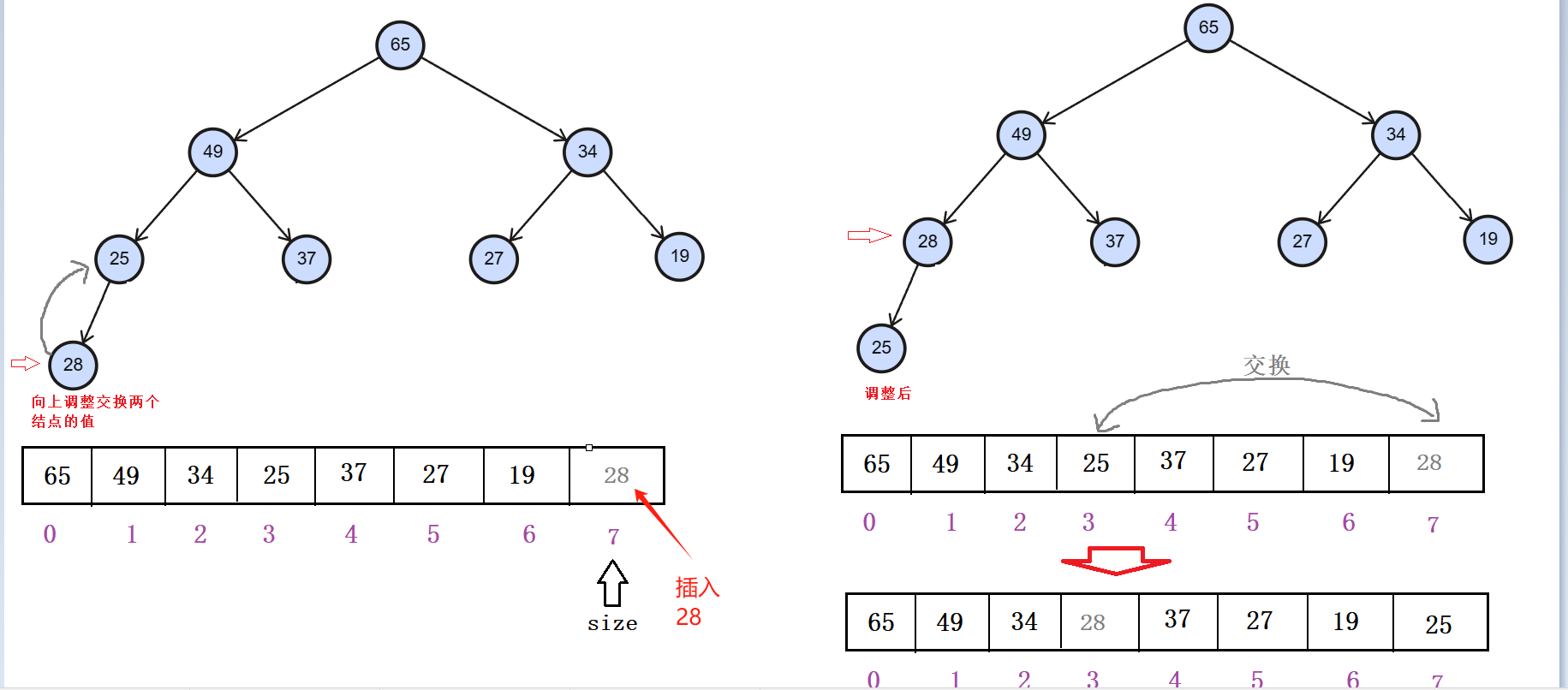
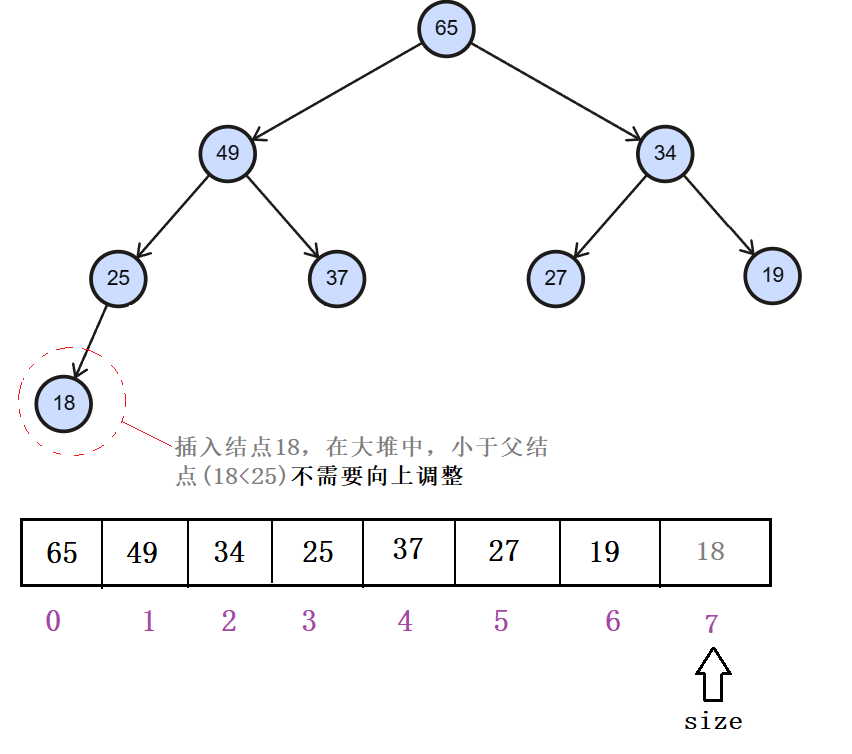
2. 当小于等于时,不需要调整
代码
//向上调整
void AdjustUp(HPDataType * a,int child)
{//先找到父结点的下标int parent = (child - 1) / 2;while (child > 0) //child等于0时,说明已经调整ok了{if (a[child] > a[parent]){swap(&a[child], &a[parent]);//可能会向上调整多次child = parent;parent = (parent - 1) / 2;}else {break;}}
}//堆的插入
void PushHeap(Heap* hp, HPDataType x)
{assert(hp);//堆满判断if (hp->capacity == hp->size) {int newcapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;HPDataType* tmp = (HPDataType*)realloc(hp->a,sizeof(HPDataType)*newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}hp->a = tmp;hp->capacity = newcapacity;}//堆元素的插入hp->a[hp->size] = x;hp->size++;//堆的向上调整AdjustUp(hp->a,hp->size-1);
}
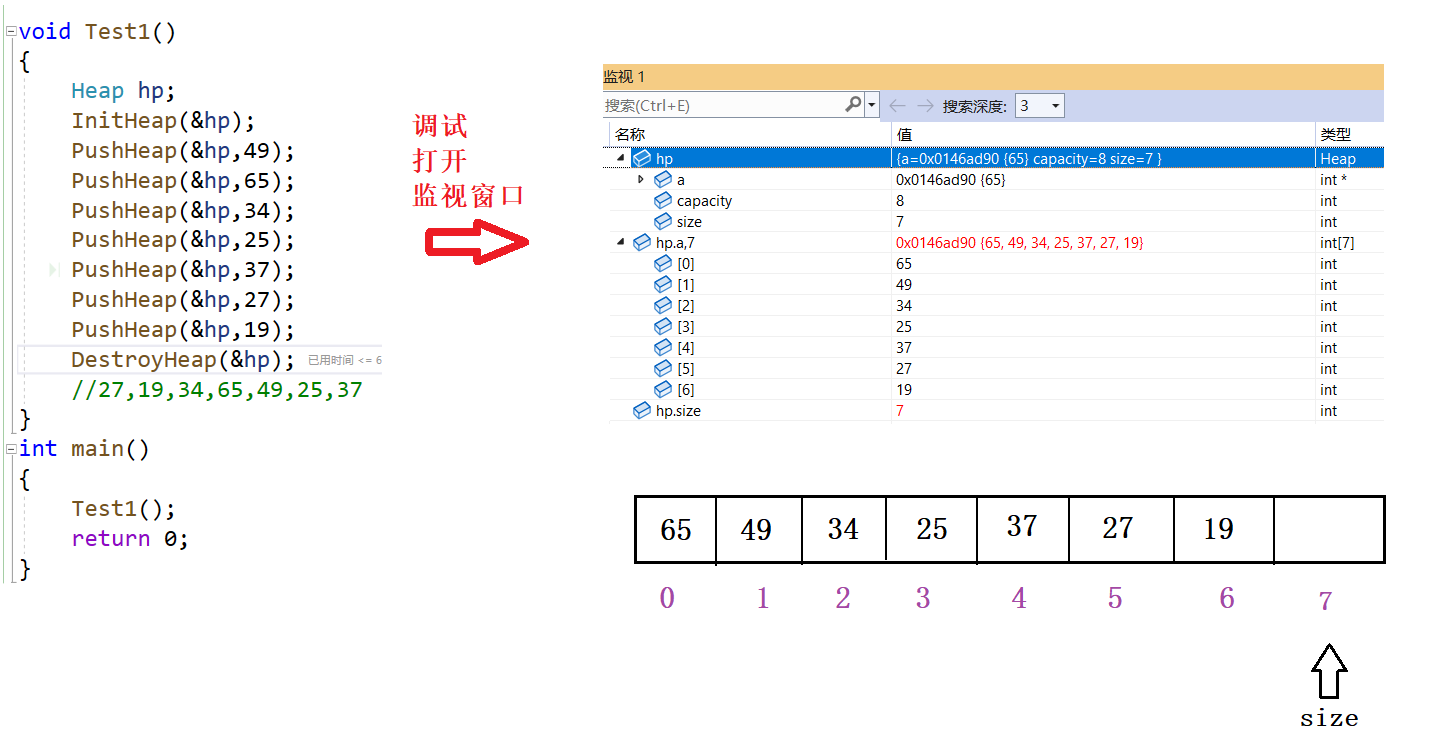
调试,查看一下数据存储情况
5. 堆的删除
堆中元素的删除,发现直接删除尾结点是简单的(size减一即可),但是,一般堆,删除元素都是删除的头结点。
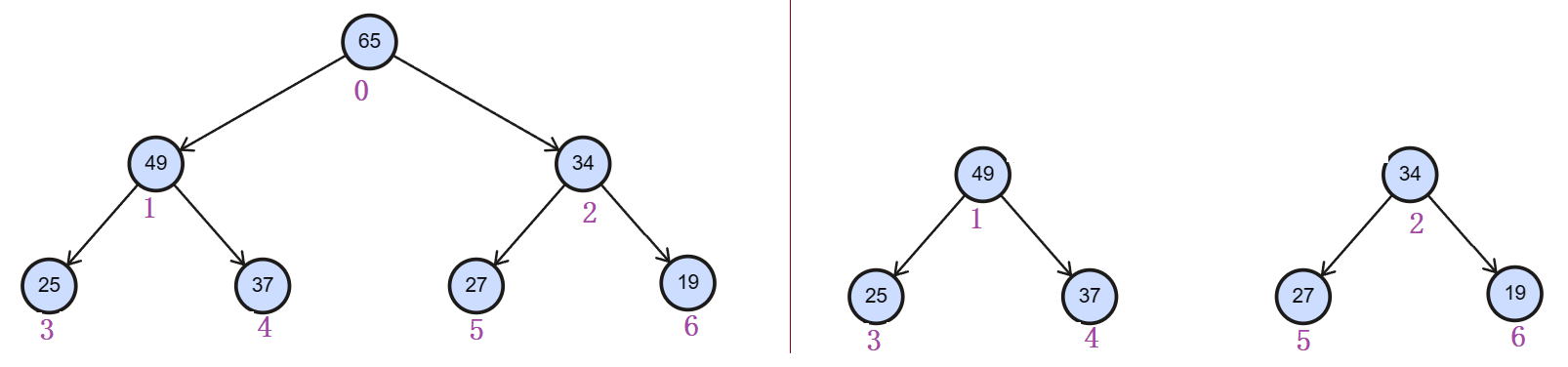
直接删除头结点时:发现逻辑结构上变成了两棵树,这样直接删除头结点的方法不推荐。
交换结点再删除
头尾结点交换后,再删除尾结点,然后头结点使用堆的向下调整算法,调堆。
使用前提就是,当进行交换的时候,保证左右仍是堆。第一个结点与最后一个结点的值交换后,向下调整。
向下调整算法
这里调的堆是大堆(根结点的值大于左右孩子结点的值)
- 第一步,找到第一个根结点的孩子结点,这里使用假设法,先让左孩子的值最大,再进行判断左孩子还是右孩子的值是最大的,找出大的。
- 第二步与根结点进行比较,大于根结点就交换。
- 及时更新父结点和孩子结点的下标
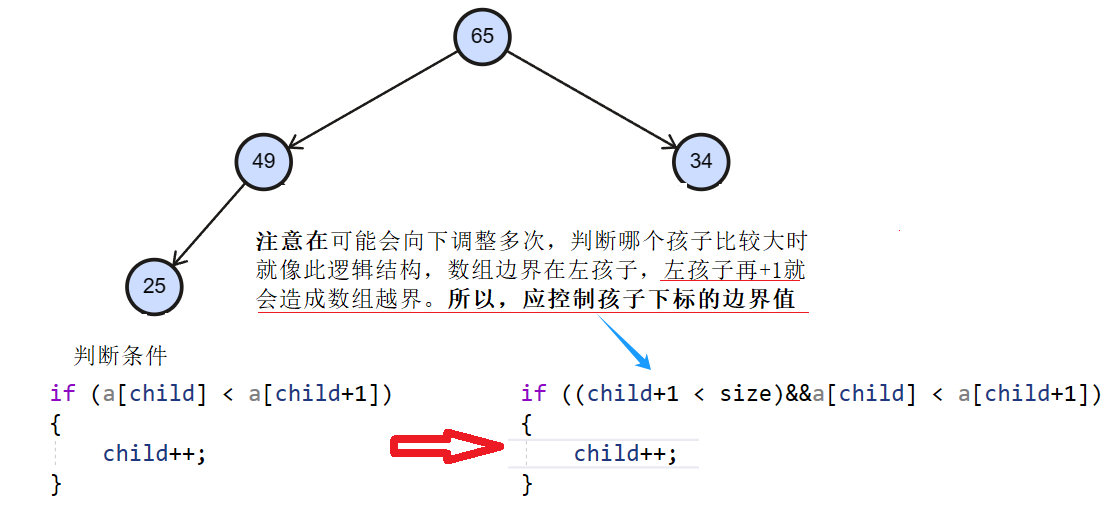
- 注意当孩子结点值都小于父亲结点值就跳出循环;循环结束条件:孩子结点的下标大于数组最大的下标(就是孩子下标<数组的个数,child<size,大于等于时说明循环就结束了)。
过程:
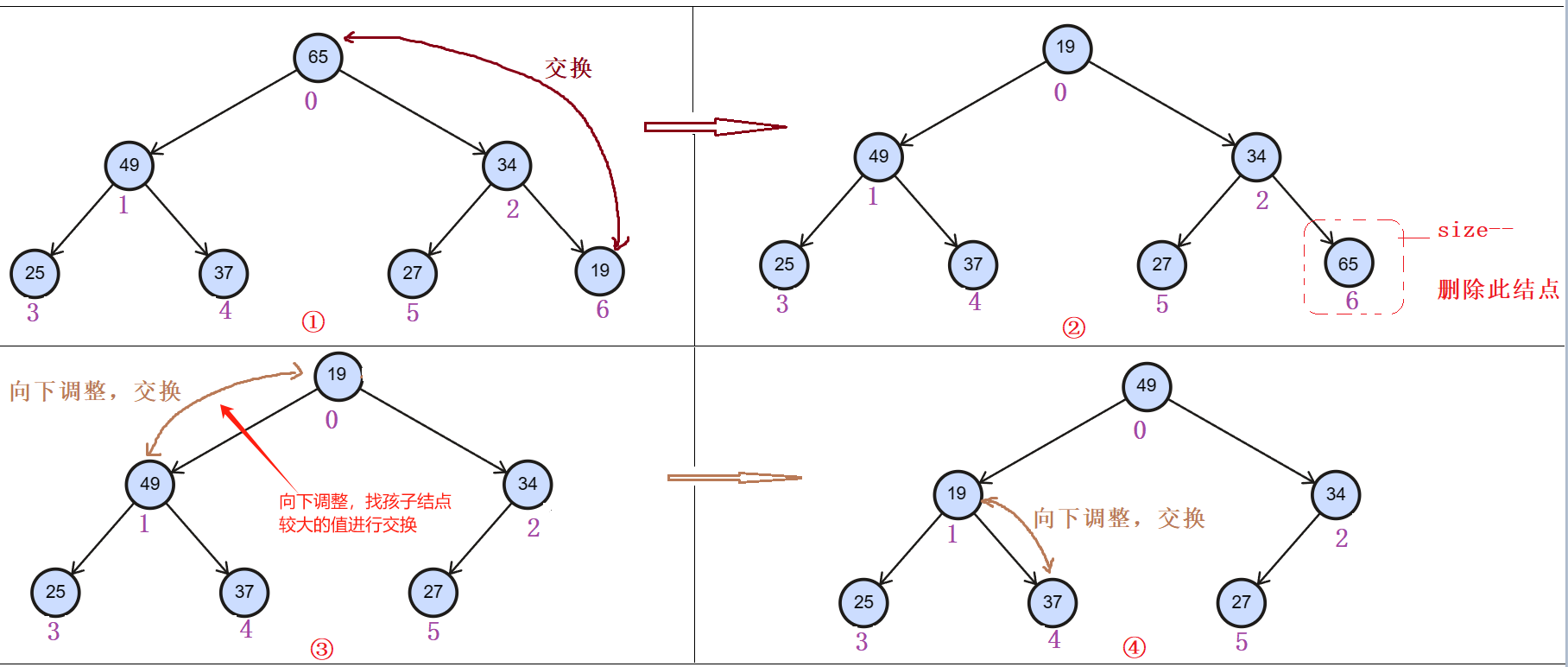
调整后
这样就完成堆头结点的删除。
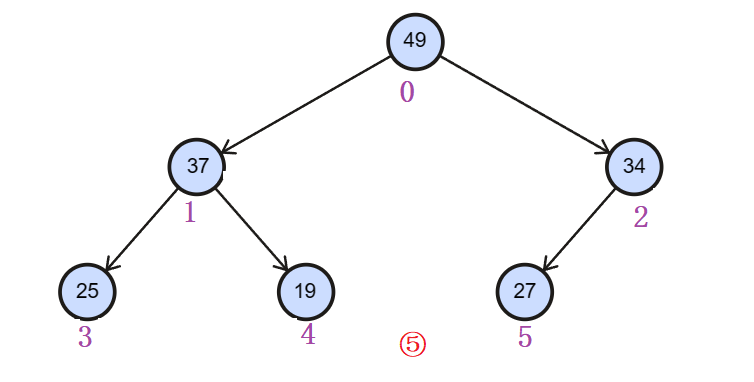
还需要注意的就是:
代码
//向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{//先去找根结点的较大的孩子结点int child = 2 * parent + 1;//可能会向下调整多次while (child<size) {//这里使用假设法,先假设左孩子的值最大//如果不对就进行更新if ((child+1 < size)&&a[child] < a[child+1]) {child++;}//根结点与其孩子结点中的较大的一个进行交换if(a[child] > a[parent]) {swap(&a[child],&a[parent]);//更新下标parent = child;child = 2 * parent + 1;}else {break; //调完堆}}
}
//堆的删除
void PopHeap(Heap* hp)
{assert(hp);assert(hp->size>0);//头尾交换swap(&hp->a[0],&hp->a[hp->size-1]);hp->size--;//向下调整AdjustDown(hp->a,hp->size,0);
}
调试一下:

上图中指向下标6其实有数据65的,但是数组的下标有效范围在0-5
6. 获取堆顶数据
前提:堆得有数据
代码
//获取堆顶数据
HPDataType TopHeap(Heap* hp)
{assert(hp);assert(hp->size>0);return hp->a[0];
}
7. 获取堆的数据个数
代码
//获取堆的数据个数
int SizeHeap(Heap* hp)
{assert(hp);return hp->size;
}
8. 堆的判空
代码
//堆的判空
bool EmptyHeap(Heap* hp)
{assert(hp);return hp->size == 0;
}
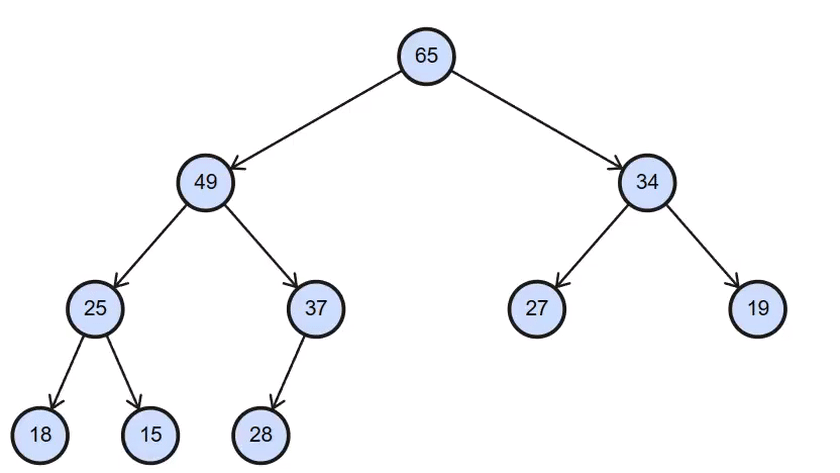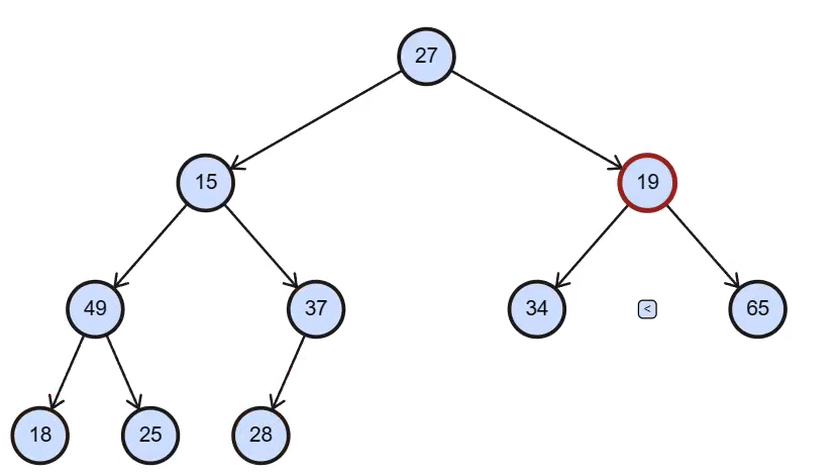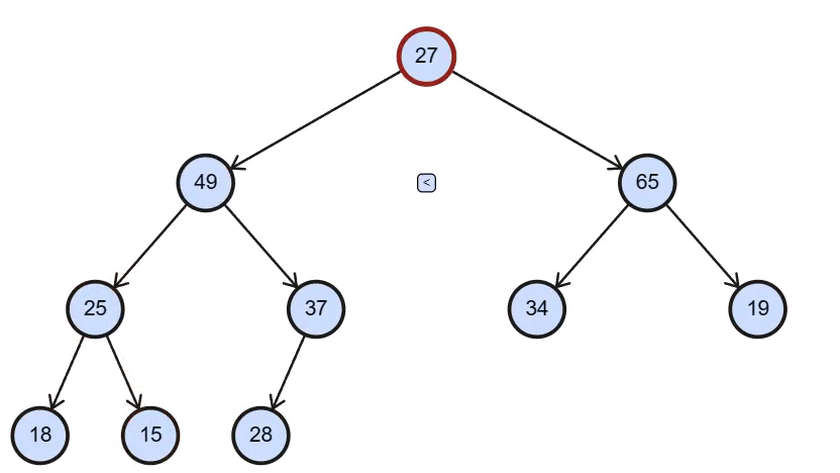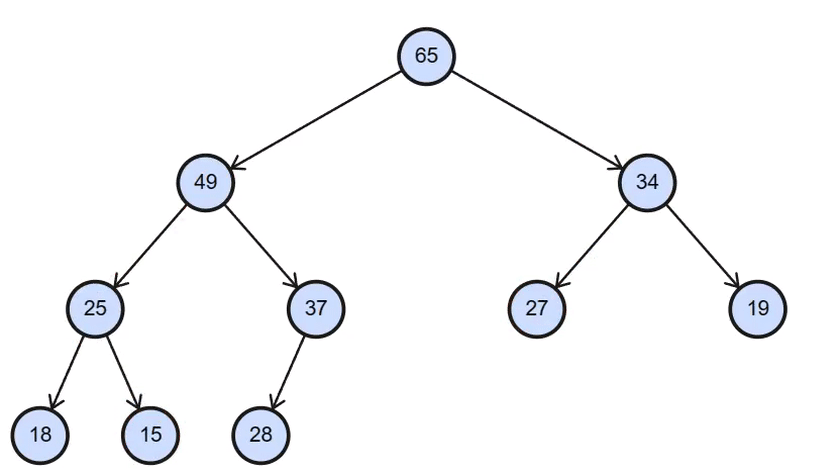
二、Gif演示
调堆演示
三、 堆排序
堆排序是一种选择排序。
堆排序:可以从小到大进行排序(使用大堆)。Top k 问题:取出最大的前k个值。
1. 堆排序
堆排序(Heap Sort)是一种基于完全二叉树的排序算法,它通过将待排序的元素建成一个二叉堆。堆排序的时间复杂度为O(nlogn),它是不稳定排序算法。
堆排序的思路如下:
- 以升序排序为例,先建立一个大堆(父节点的值大于子节点的值),将待排序的元素都插入堆中。
- 将堆顶元素(最大值)与堆末尾元素交换,然后将堆的大小减1。
- 对堆顶元素向下调整操作,使得堆重新满足最大堆的性质。
- 重复2-3步,直到堆的大小为1。排序完成。
(1) 建大堆
使用 向下 调整算法来向上建堆:使用向下调整算法,把数组调成大堆
因为堆本身是一个完全二叉树,假设一共有h层,我们从第h-1层(即不是叶子结点的那一层开始)
因为是大堆,根结点的值大于孩子结点的值,从最下方使用向下调整来不断把较大的值来调到根节点。
注意:虽然使用的是向下调整算法,其实还是不断往上调整(把大的值调到上面)。
如图:
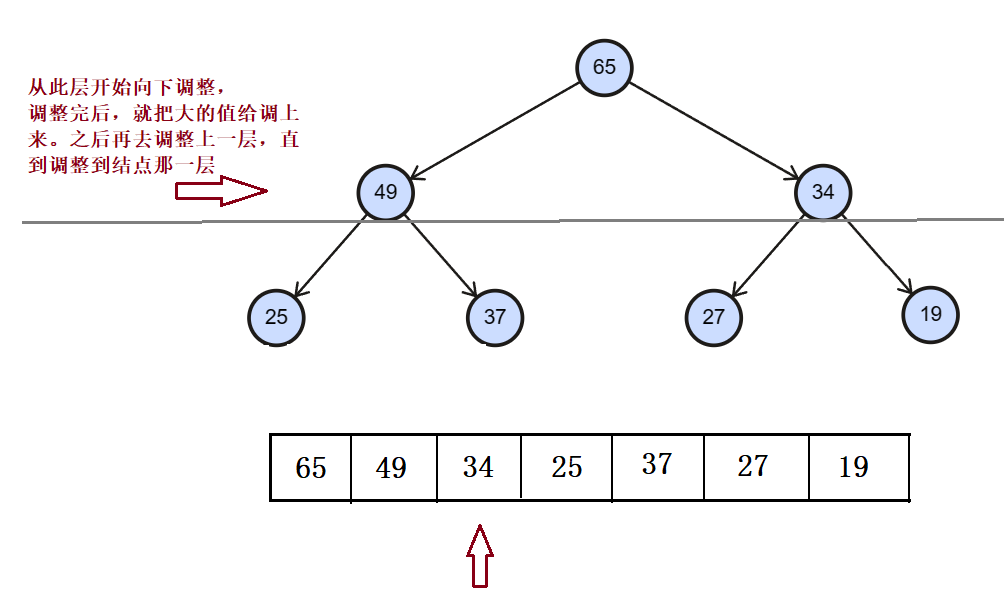
直到调整到第一层为止
建堆时间复杂度:O(N)
//堆排序
void HeapSort(int* arr, int n)
{int i = 0;//使用向下调整算法向上调整,把大的值调到上方。for (i = (n - 1 - 1) / 2; i >= 0;i--){//先找到数组最后端的父结点的下标//父结点的下标减一就是另一个//使用向下调整算法进行调整AdjustDown(arr,n,i);}
}
当然也可以用向上算法进行向上建堆。
思路:先让一个独自成堆,然后尾插一个结点,再进行与根结点进行比较,大于根结点的值就交换。
但是这个使用向上调整算法向上建堆的时间复杂度为:O(Nlog(N))
//向上调整算法进行堆排序
void HeapSort(int* arr, int n)
{int i = 0;//先让第一个结点独自成堆//再一次尾增结点进行向上调整for (i = 1; i < n; i++) {AdjustUp(arr,i);}
}
(2) 排序
因为建成大堆后,将堆顶元素(最大值)与堆末尾元素交换
//注意end 是从n-1开始的(数组最后一个元素的下标)int end = n-1;while (end > 0) {//swap end = n-1 这表示下标swap(&arr[0],&arr[end]);//adjustdown 函数里面的end是元素的个数,所以不是先--end//所以AdjustDown(arr,end,0);end--;}
注意这里的end–,上述是从数组最后一个元素下标n-1 开始。堆的首元素与尾元素交换完后,接着就是堆的个数减1,然后下进行向下调整。这里的end–放在了最后。因为AdjustDown中的第二个参数是传的是堆的大小,正好数组下标n-1 , 堆由n减一也是 n -1。
下方给出了 end 从n 开始的优化,但是可读性就会下降
void HeapSort(int* arr, int n)
{int i = 0;//先建成一个大堆for (i = (n - 1 - 1) / 2; i >= 0;--i) {AdjustDown(arr,n,i);}//堆顶元素与堆尾元素进行交换,进而把大的元素放到后面int end = n;while (end > 0) {swap(&arr[--end],&arr[0]);AdjustDown(arr,end,0);}
}
2.Topk问题
topk问题,例如:在10000个数据排名中找出前10;或者在10000个数中找出最大的前10个
这里我们就以在10000个数中找出最大的前10(k = 10)个为例
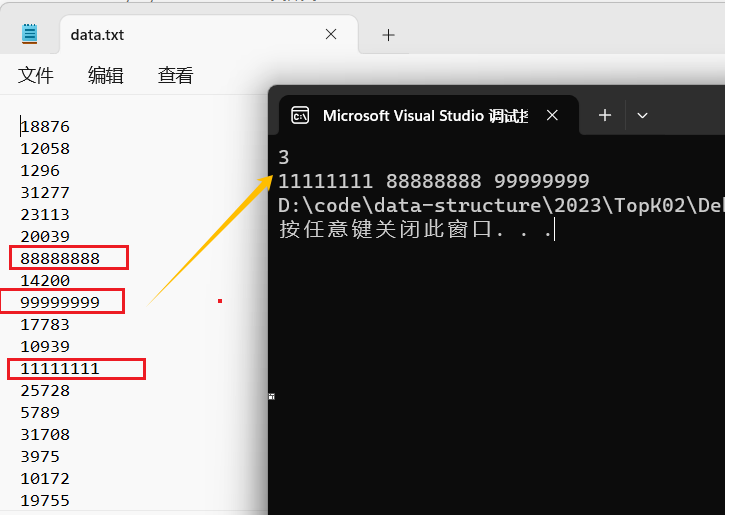
首先应先准备数据,随机生成10000个数(注意srand函数只能生成30000多个随机数)
核心思想: 建一个可以存储k个数据的小堆。先把文件数据前10个数据读取到小堆中(进行向下调成小堆),然后再把文件中的其他数据一个一个读出与小堆的根结点的值进行比较,如果大于小堆的根结点,就进放入堆中,然后进行向下调堆。
//创建数据
void Createdata()
{int n = 10000;srand((unsigned)time(0));const char* file = "data.txt";FILE* fin = fopen(file,"w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n;i++){int x = (rand() + i) % 100000;//把随机生成的数据写到fin文件中去fprintf(fin,"%d\n",x);}fclose(fin);
}
void PrintTopK(int k)
{//从文件中读出数据const char* file = "data.txt";FILE* fout = fopen(file,"r");if (fout == NULL){perror("fout error");return;}//将数据读出到容量为k的动态数组中int* arr = (int*)malloc(sizeof(int)*k);if (arr == NULL){perror("malloc error");exit(-1);}//先把前k个数据放入数组中for (int i = 0; i < k; i++){//将数据读到数组中fscanf(fout,"%d",&arr[i]);//放数据的同时进行建堆AdjustUp(arr,i);}int x = 0;//当文件里面的数据读完后会返回EOFwhile (fscanf(fout, "%d", &x) != EOF) {//当从文件拿出的数据大于小堆中的数据时//将数据放到小堆中//并使用向下调整//这样每次来的比较大的数据就可以放到小堆中if (x > arr[0]) {arr[0] = x;AdjustDown(arr,k,0);}}//打印数据for (int i = 0; i < k;i++) {printf("%d ",arr[i]);}fclose(fout);}
四、完整代码
1.堆的代码
Heap.c
#include "Heap.h"//初始化堆
void InitHeap(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}//销毁堆
void DestroyHeap(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = hp->size = 0;
}//交换两个数
void swap(HPDataType* s1,HPDataType* s2)
{HPDataType tmp = *s1;*s1 = *s2;*s2 = tmp;
}
//向上调整
void AdjustUp(HPDataType * a,int child)
{//先找到父结点的下标int parent = (child - 1) / 2;while (child > 0) //child等于0时,说明已经调整ok了{if (a[child] > a[parent]){swap(&a[child], &a[parent]);//可能会向上调整多次child = parent;parent = (parent - 1) / 2;}else {break;}}
}//堆的插入
void PushHeap(Heap* hp, HPDataType x)
{assert(hp);//堆满判断if (hp->capacity == hp->size) {int newcapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;HPDataType* tmp = (HPDataType*)realloc(hp->a,sizeof(HPDataType)*newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}hp->a = tmp;hp->capacity = newcapacity;}//堆元素的插入hp->a[hp->size] = x;hp->size++;//堆的向上调整AdjustUp(hp->a,hp->size-1);
}//向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{//先去找根结点的较大的孩子结点int child = 2 * parent + 1;//可能会向下调整多次while (child<size) {//这里使用假设法,先假设左孩子的值最大//如果不对就进行更新if ((child+1 < size)&&a[child] < a[child+1]) {child++;}//根结点与其孩子结点中的较大的一个进行交换if(a[child] > a[parent]) {swap(&a[child],&a[parent]);//更新下标parent = child;child = 2 * parent + 1;}else {break; //调完堆}}
}
//堆的删除
void PopHeap(Heap* hp)
{assert(hp);assert(hp->size>0);//头尾交换swap(&hp->a[0],&hp->a[hp->size-1]);hp->size--;//向下调整AdjustDown(hp->a,hp->size,0);
}//获取堆顶数据
HPDataType TopHeap(Heap* hp)
{assert(hp);assert(hp->size>0);return hp->a[0];
}//获取堆的数据个数
int SizeHeap(Heap* hp)
{assert(hp);return hp->size;
}//堆的判空
bool EmptyHeap(Heap* hp)
{assert(hp);return hp->size == 0;
}
Heap.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a; //指向动态数组int capacity; //堆的容量int size; //堆中数据个数
}Heap;//初始化堆
void InitHeap(Heap* hp);//销毁堆
void DestroyHeap(Heap* hp);//堆的插入
void PushHeap(Heap* hp, HPDataType x);//堆的删除
void PopHeap(Heap*hp);//获取堆顶数据
HPDataType TopHeap(Heap* hp);//获取堆的数据个数
int SizeHeap(Heap* hp);//堆的判空
bool EmptyHeap(Heap* hp);
test.c
#include "Heap.h"void Test1()
{Heap hp;InitHeap(&hp);PushHeap(&hp,49);PushHeap(&hp,65);PushHeap(&hp,34);PushHeap(&hp,25);PushHeap(&hp,37);PushHeap(&hp,27);PushHeap(&hp,19);//删除65PopHeap(&hp);//printf("堆的个数:%d\n",SizeHeap(&hp));//while (!EmptyHeap(&hp)) //{// printf("%d-", TopHeap(&hp));// PopHeap(&hp);//}DestroyHeap(&hp);//27,19,34,65,49,25,37
}
int main()
{Test1();return 0;
}
2. 堆排序的代码
//堆排序
void HeapSort(int* arr, int n)
{int i = 0;//使用向下调整算法向上调整,把大的值调到上方。for (i = (n - 1 - 1) / 2; i >= 0;i--){//先找到数组最后端的父结点的下标//父结点的下标减一就是另一个//使用向下调整算法进行调整AdjustDown(arr,n,i);}//进行排序//因为是大堆,所以根结点的值是最值//把最值与堆的最后一个结点进行交换//再把交换后的根节点进行向下调整//然后堆的大小减一//注意end 是从n-1开始的(数组最后一个元素的下标)int end = n-1;while (end > 0) {//swap end = n-1 这表示下标swap(&arr[0],&arr[end]);//adjustdown 函数里面的end是元素的个数,所以不是先--end//所以AdjustDown(arr,end,0);end--;}
}
相关文章:

堆和堆排序【数据结构】
目录 一、堆1. 堆的存储定义2. 初始化堆3. 销毁堆4. 堆的插入向上调整算法 5. 堆的删除向下调整算法 6. 获取堆顶数据7. 获取堆的数据个数8. 堆的判空 二、Gif演示三、 堆排序1. 堆排序(1) 建大堆(2) 排序 2.Topk问题 四、完整代码1.堆的代码Heap.cHeap.htest.c 2. 堆排序的代码…...
【全程录屏GPT3.5升级4.0】2024最新GPT4升级订阅详细指南
前言:为什么要升级GPT4.0,下图是来自GPT4.0的官方回答,可以看出,GPT4无愧于是一个大版本升级的。 一、视频教程 记录了普通用户使用WildCrad从GPT3.5升级到4.0的全部过程,感兴趣可以前往观看:https://www.…...
中移(苏州)软件技术有限公司面试问题与解答(4)—— virtio所创建的设备1
接前一篇文章:中移(苏州)软件技术有限公司面试问题与解答(0)—— 面试感悟与问题记录 本文参考以下文章: VirtIO实现原理——PCI基础 VirtIO实现原理——virtblk设备初始化 特此致谢! 本文对…...
》笔记5)
《动手学深度学习(PyTorch版)》笔记5
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过,…...

QT中wchar_t类型如何输出
在Qt中,通常使用QString来处理字符串,而不是wchar_t。QString是Qt中用于处理Unicode字符串的类。如果你有wchar_t类型的字符串,你可以将其转换为QString进行输出。 以下是一个简单的例子: #include <QCoreApplication> #i…...
网络安全04-sql注入靶场第一关
目录 一、环境准备 1.1我们进入第一关也如图: 编辑 二、正式开始第一关讲述 2.1很明显它让我们在标签上输入一个ID,那我们就输入在链接后面加?id1 编辑 2.2链接后面加个单引号()查看返回的内容,127.0.0.1/sqli/less-1/?id1,id1 …...
微服务理解篇
一 :架构演变 1 单体架构: 简单理解为一个服务涵盖所有需求功能2 垂直架构: 按照业务功能将单体架构拆分成小模块服务, 如:订单系统,用户系统,商品系统 ##缺点 引入分布式事务,分布式锁等,优点:模块解耦## 垂直拆分:根据业务层级拆分,比如商城的订单系统,用户系统,商品系统…...

项目篇:基于TCP通信模型的外卖软件实现
一、基本成员及功能实现 本项目主要由服务器,消费者,商家,外卖员组成。基本的功能如下。 对所有人: 1、可以注册登录 2、可以修改个人信息 3、可以销户 商家: 1、注册时需要填写售卖商品信息 2、可以修改商品信…...

深入浅出 diffusion(2):pytorch 实现 diffusion 加噪过程
我在上篇博客深入浅出 diffusion(1):白话 diffusion 原理(无公式)中介绍了 diffusion 的一些基本原理,其中谈到了 diffusion 的加噪过程,本文用pytorch 实现下到底是怎么加噪的。 import torch…...
【软件测试】学习笔记-构建并执行 JMeter 脚本的正确姿势
有些团队在组建之初往往并没有配置性能测试人员,后来随着公司业务体量的上升,开始有了性能测试的需求,很多公司为了节约成本会在业务测试团队里选一些技术能力不错的同学进行性能测试,但这些同学也是摸着石头过河。他们会去网上寻…...
iOS 面试 Swift基础题
一、Swift 存储属性和计算属性比较: 存储型属性:用于存储一个常量或者变量 计算型属性: 计算性属性不直接存储值,而是用 get / set 来取值 和 赋值,可以操作其他属性的变化. 计算属性可以用于类、结构体和枚举,存储属性只能用于类和结构体。存储属性可…...

(七)for循环控制
文章目录 用法while的用法for的用法两者之间的联系可以相互等价用for改写while示例for和while的死循环怎么写for循环见怪不怪表达式1省略第一.三个表达式省略(for 改 while)全省略即死循环(上面已介绍) 用法 类比学习while语句 …...
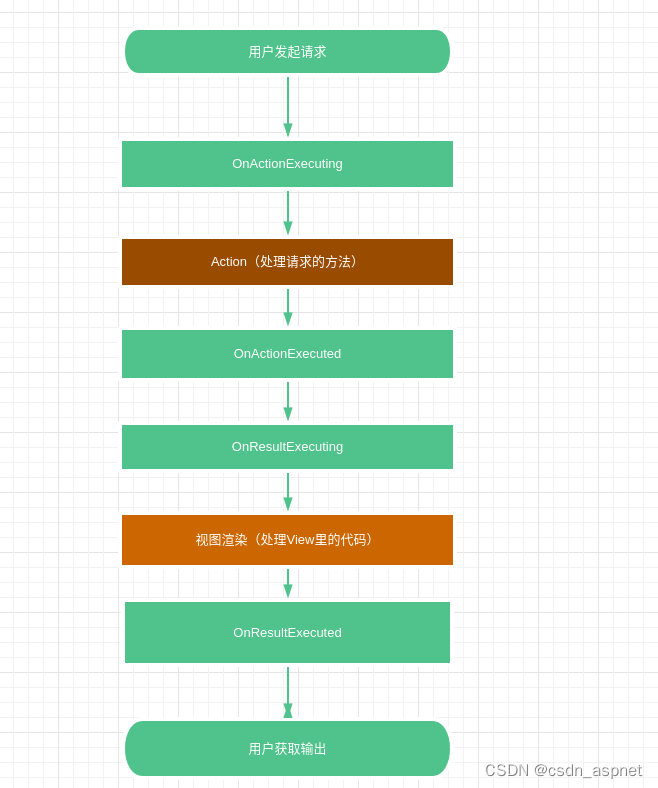
ASP .NET Core Api 使用过滤器
过滤器说明 过滤器与中间件很相似,过滤器(Filters)可在管道(pipeline)特定阶段(particular stage)前后执行操作。可以将过滤器视为拦截器(interceptors)。 过滤器级别范围…...
CodeGPT--(Visual )
GitCode - 开发者的代码家园 gitcode.com/ inscode.csdn.net/liujiaping/java_1706242128563/edit?openFileMain.java&editTypelite marketplace.visualstudio.com/items?itemNameCSDN.csdn-codegpt&spm1018.2226.3001.9836&extra%5Butm_source%5Dvip_chatgpt_c…...
1.Mybatis入门
目录 前言 1入门 1.1 入门程序实现 1.2 数据准备 编辑 1.3 配置Mybatis 1.4 编写SQL语句 1.5 单元测试 1.6 解决SQL警告与提示 2. JDBC介绍(了解) 2.1 介绍 2.2 代码 2.3 问题分析 2.4 技术对比 3. 数据库连接池 3.1 介绍 3.2 产品 4. lombok 4.1 介绍 4.…...
android camera系列(Camera1、Camera2、CameraX)的使用以及输出的图像格式
一、Camera 1.1、结合SurfaceView实现预览 1.1.1、布局 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-au…...

live555搭建流式rtsp服务器
源代码已上传gitee 一、需求 live555源代码中的liveMediaServer是将本地文件作为源文件搭建rtsp服务器,我想用live555封装一个第三方库,接收流数据搭建Rtsp服务器;预想接口如下: class LiveRtspServer { public:/***brief构造一…...

Apache孵化器领路人与导师的职责
对于捐赠到 ASF 孵化器的项目来说, ASF 孵化器项目管理委员会(IPMC)的成员会扮演两个角色,一个 孵化器领路人(Champion),另外一个是孵化器导师(Mentor)。 本文源自 ALC …...
【C++中STL】set/multiset容器
set/multiset容器 Set基本概念set构造和赋值set的大小和交换set的插入和删除set查找和统计 set和multiset的区别pair对组两种创建方式 set容器排序 Set基本概念 所有元素都会在插入时自动被排序。 set/multist容器属于关联式容器,底层结构属于二叉树。 set不允许容…...

使用 create-react-app 创建 react 应用
一、创建项目并启动 第一步:全局安装:npm install -g create-react-app 第二步:切换到想创建项目的目录,使用命令create-react-app hello-react 第三步:进入项目目录,cd hello-react 第四步:启…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
