数论与图论
数论🎈
筛质数
最普通的筛法O(nlogn):
void get_primes2(){for(int i=2;i<=n;i++){if(!st[i]) primes[cnt++]=i;//把素数存起来for(int j=i;j<=n;j+=i){//不管是合数还是质数,都用来筛掉后面它的倍数st[j]=true;}}
}诶氏筛法 O(nloglogn):
void get_primes1(){for(int i=2;i<=n;i++){if(!st[i]){primes[cnt++]=i;for(int j=i;j<=n;j+=i) st[j]=true;//可以用质数就把所有的合数都筛掉;}}
}线性筛O(n)
void get_primes(){//外层从2~n迭代,因为这毕竟算的是1~n中质数的个数,而不是某个数是不是质数的判定for(int i=2;i<=n;i++){if(!st[i]) primes[cnt++]=i;for(int j=0;primes[j]<=n/i;j++){//primes[j]<=n/i:变形一下得到——primes[j]*i<=n,把大于n的合数都筛了就//没啥意义了st[primes[j]*i]=true;//用最小质因子去筛合数//1)当i%primes[j]!=0时,说明此时遍历到的primes[j]不是i的质因子,那么只可能是此时的primes[j]<i的//最小质因子,所以primes[j]*i的最小质因子就是primes[j];//2)当有i%primes[j]==0时,说明i的最小质因子是primes[j],因此primes[j]*i的最小质因子也就应该是//prime[j],之后接着用st[primes[j+1]*i]=true去筛合数时,就不是用最小质因子去更新了,因为i有最小//质因子primes[j]<primes[j+1],此时的primes[j+1]不是primes[j+1]*i的最小质因子,此时就应该//退出循环,避免之后重复进行筛选。if(i%primes[j]==0) break;}}}
试除法判断质数
输入n表示要判断的n个数,接下来输入n个数,判断其是否为质数
#include<bits/stdc++.h>
using namespace std;
int n;
bool isprime(long long a){if(a==1){return 0;}else if(a==2){return 1;}for(int i=2;i<=a/i;i++){//不要用开方或者i*i,开方函数较慢,i*i会越界if(a%i==0){return 0;}}return 1;
}
int main(){cin>>n;while(n--){long long a;cin>>a;if(isprime(a)) cout<<"Yes"<<endl;else cout<<"No"<<endl;}分解质因数
解题思路:
- x 的质因子最多只包含一个大于 根号x 的质数。如果有两个,这两个因子的乘积就会大于 x,矛盾。
- i 从 2 遍历到 根号x。 用 x / i,如果余数为 0,则 i 是一个质因子。
- s 表示质因子 i 的指数,x /= i 为 0,则 s++, x = x / i 。
- 最后检查是否有大于 根号x 的质因子,如果有,输出。
#include <iostream>
#include <algorithm>using namespace std;void divide(int x)
{for (int i = 2; i <= x / i; i ++ )//i <= x / i:防止越界,速度大于 i < sqrt(x)if (x % i == 0)//i为底数{int s = 0;//s为指数while (x % i == 0) x /= i, s ++ ;cout << i << ' ' << s << endl;//输出}if (x > 1) cout << x << ' ' << 1 << endl;//如果x还有剩余,单独处理cout << endl;
}
{
int main()
{int n;cin >> n;while (n -- ){int x;cin >> x;divide(x);}return 0;
}相关文章:

数论与图论
数论🎈 筛质数 最普通的筛法O(nlogn): void get_primes2(){for(int i2;i<n;i){if(!st[i]) primes[cnt]i;//把素数存起来for(int ji;j<n;ji){//不管是合数还是质数,都用来筛掉后面它的倍数st[j]true;}} } 诶氏筛法 O(nloglogn)&#…...

海外云手机三大优势
在全球化潮流下,企业因业务需求对海外手机卡等设备的需求不断攀升,推动了海外云手机业务的蓬勃发展。相较于自行置备手机设备,海外云手机不仅能够降低成本,还具备诸多优势,让我们深入探讨其中的三大黄金优势。 经济实惠…...

AndroidStudio安装教程基础篇
Android Studio是专为Android应用程序开发而设计的官方集成开发环境(IDE)。它提供了丰富的工具和功能,帮助开发者更高效地构建出色的应用程序。本文将为您提供Android Studio的安装文档基础指南,帮助您顺利安装并开始使用这款强大…...
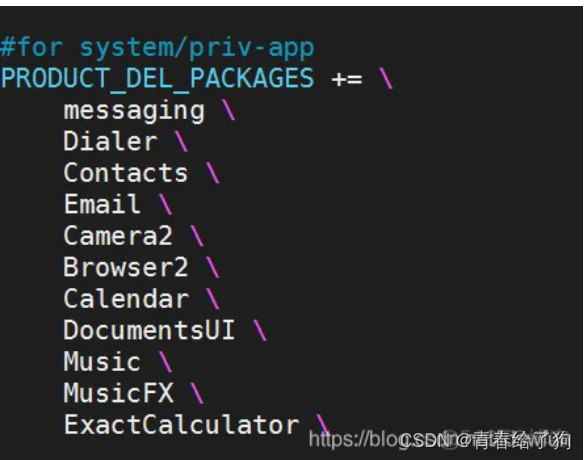
RK3568 Android 13 系统裁剪
android 13 系统裁剪是个大工程,裁剪也是需要大量的测试,才能保证系统的稳定性,以下是RK官方给出的裁剪方案,有兴趣的可以去看一下,对裁剪不是要求过高的可以根据官方的建议,对系统进行裁剪: Rockchip And…...

Ubuntu 隐藏Telnet主机SSH服务时显示版本信息问题
一、背景 默认情况下,我们通过telnet服务器的22端口,能够获取OpenSSH服务的banner信息(如下图所示)。而低版本的OpenSSH存在许多高危漏洞。。为了安全我们要隐藏这个信息。 二、隐藏Telnet版本信息 当使用telnet命令,telnet 192.168.31.20…...

webpack环境配置
1.首先安装 cross-env npm install cross-env --save-dev 在package.json里面配置 根据不同命令打包 "scripts": {"dev": "cross-env NODE_ENVdevelopment webpack-dev-server --config webpack.config.dev.js","dev:test": "c…...

树控件、下拉框、文本框常用测试用例
01 控件的测试外观操作 1)项目中的所有树是否风格一致 2)树结构的默认状态是怎样的。比如默认树是否是展开,是展开几级? 是否有默认的焦点?默认值是什么?展开的节点图标和颜色? 3)…...
Java把列表数据导出为PDF文件,同时加上PDF水印
一、实现效果 二、遇到的问题 实现导出PDF主体代码参考:Java纯代码实现导出PDF功能,下图是原作者实现的效果 导出报错Font STSong-Light with UniGB-UCS2-H is not recognized.。参考:itext 生成 PDF(五) 使用外部字体 网上都是说jar包的版本…...

const与readonly详解
const与readonly详解 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将深入探讨在TypeScript中常用的const与readonly关键字,了解它…...
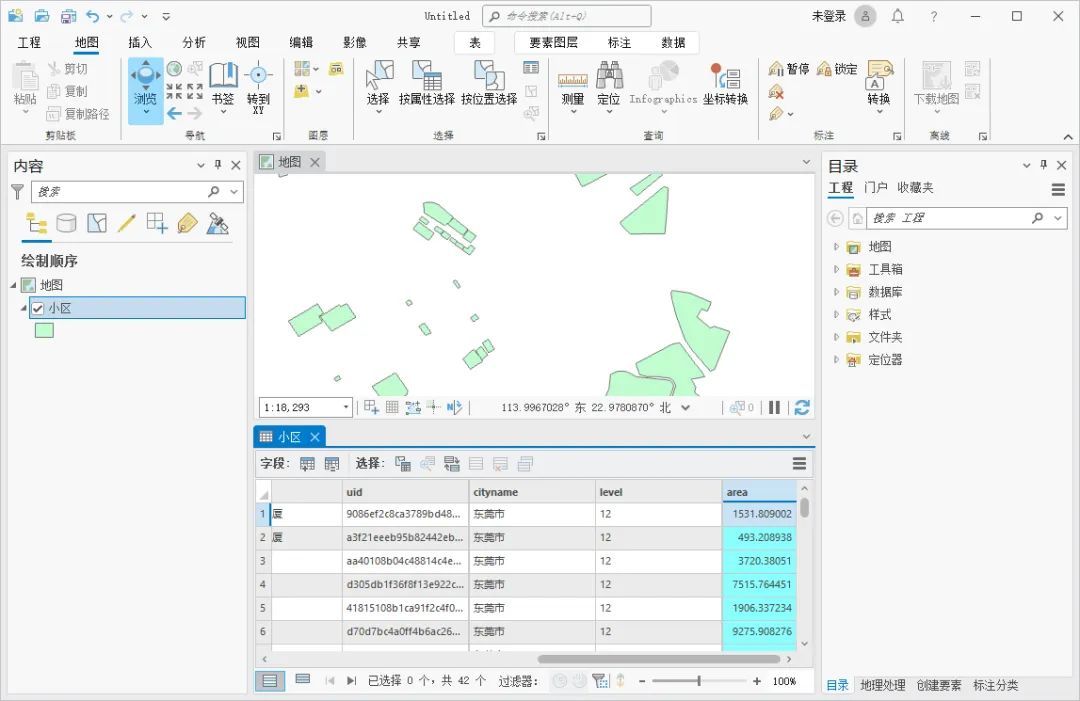
ArcGIS Pro 如何计算长度和面积等数据?
要素的几何属性属于比较重要的信息,作为一款专业的GIS软件,ArcGIS Pro自然也是带有计算几何的功能,这里为大家介绍一下计算方法,希望能对你有所帮助。 数据来源 教程所使用的数据是从水经微图中下载的矢量数据,除了矢…...
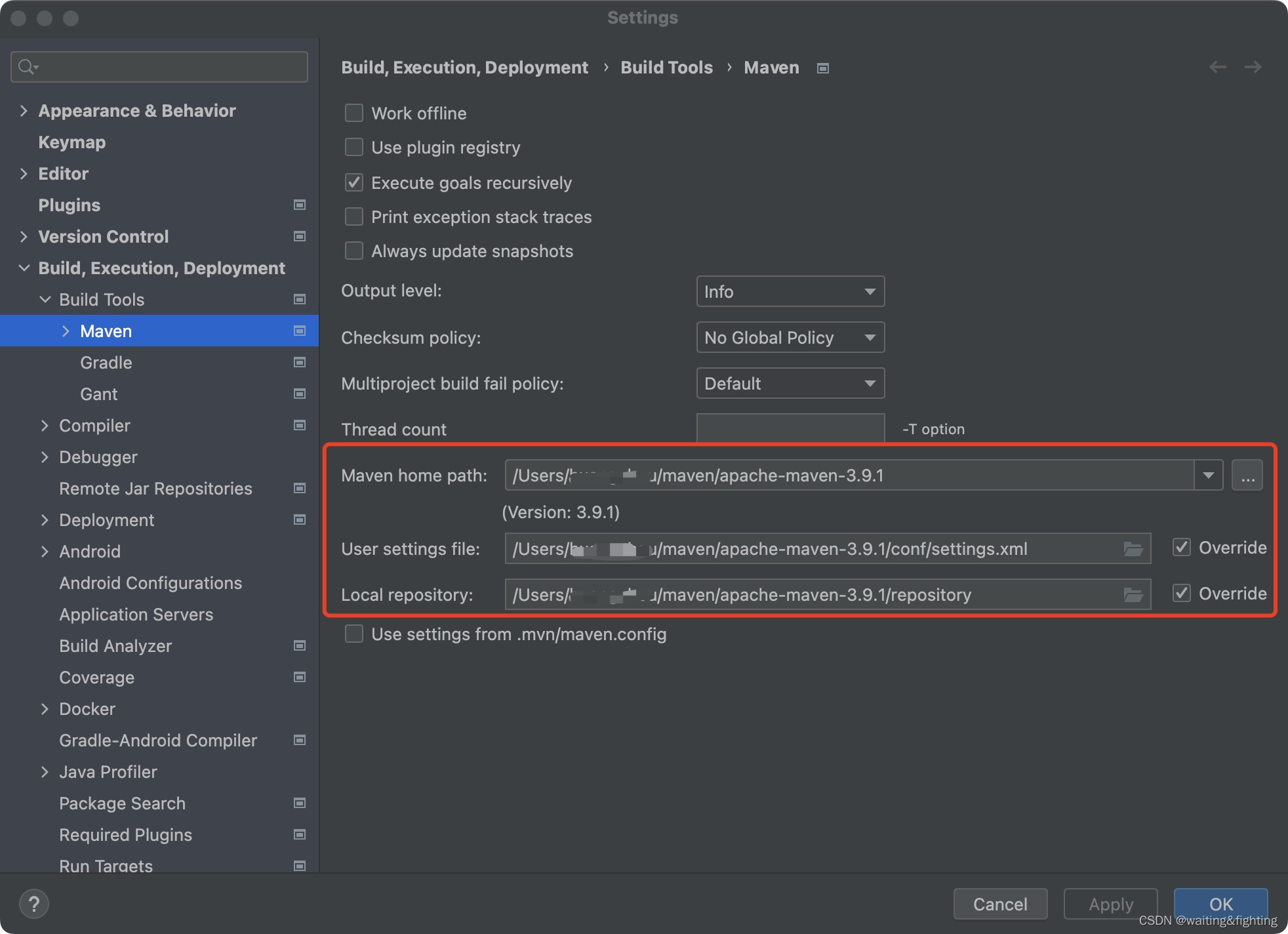
IntelliJ创建一个springboot工程
安装jdk mac教程 windows教程 安装maven mac教程 windows教程 建议: 在本地磁盘新建一个文件夹叫maven,然后把下载的maven安装到这里。在后续的IntelliJ操作中,配置maven的settings.xml和repository地址为这个目录下的地址。 创建sprin…...
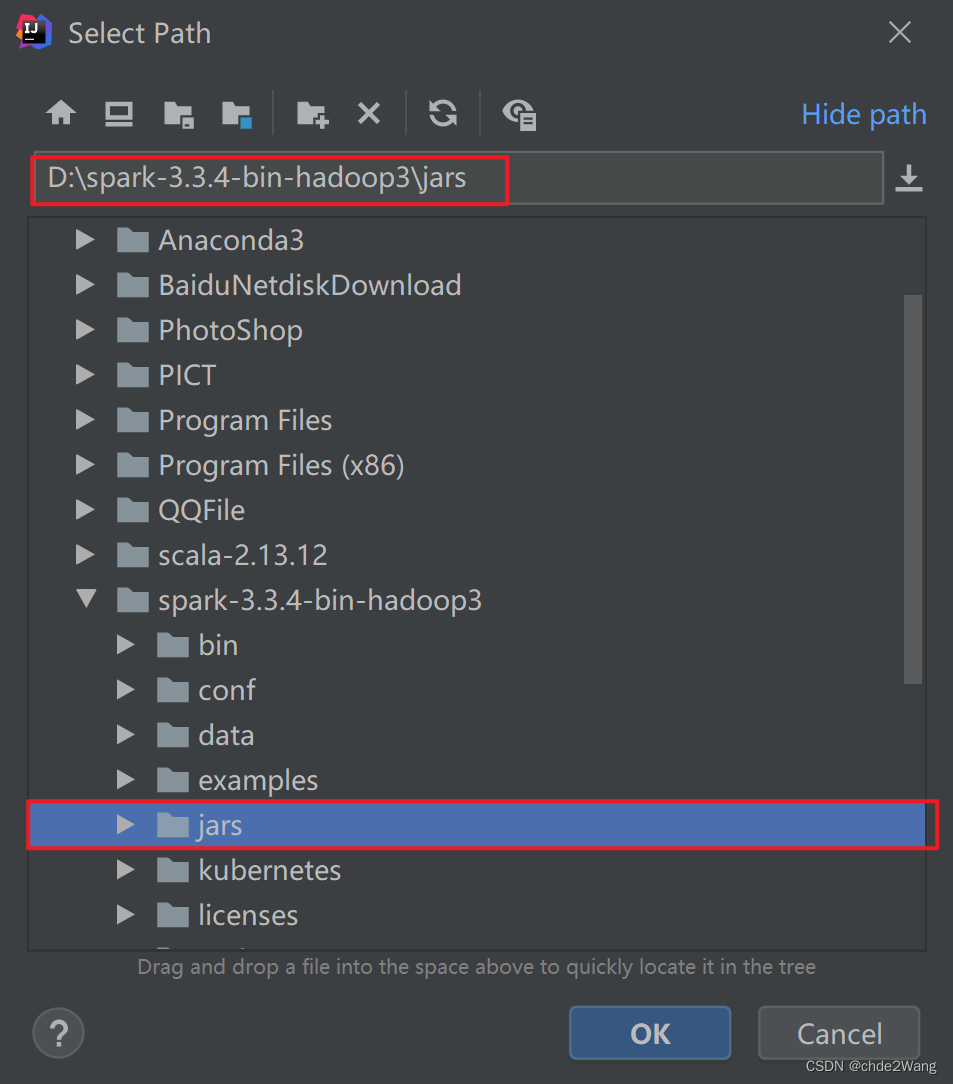
Spark入门02-Spark开发环境配置(idea环境)
安装与配置Spark开发环境 1.下载解压安装包 https://archive.apache.org/dist/spark/spark-2.1.2/ https://mirrors.tuna.tsinghua.edu.cn/apache/spark/spark-3.3.4/ 2、新建Scala项目 参考https://blog.csdn.net/weixin_38383877/article/details/135894760 3、项目中引…...
)
Codeforces Round 886 (Div. 4)
目录 A. To My Critics B. Ten Words of Wisdom C. Word on the Paper D. Balanced Round E. Cardboard for Pictures F. We Were Both Children G. The Morning Star H. The Third Letter A. To My Critics 直接模拟 void solve(){int a,b,c; cin>>a>>b&…...

Pull模式和Push模式
Pull模式是一种消息消费模式,其中客户端主动从服务端拉取数据。 优点:客户端可以根据自己的消费能力来消费数据,不存在消息堆积的情况。 缺点:消息处理可能不及时,可能存在大量无效请求,客户端需要考虑拉取…...
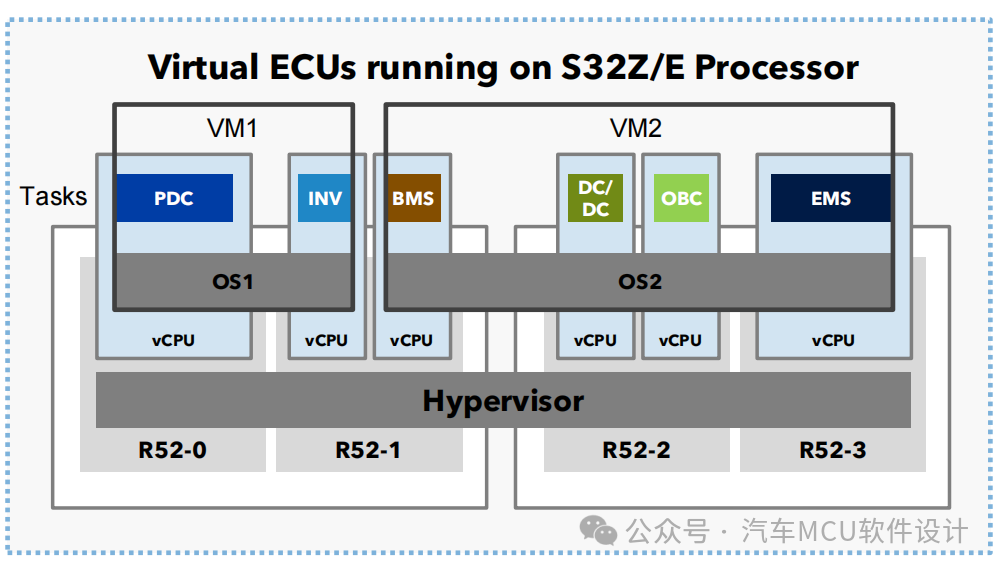
高端车规MCU的破局之路
目录 1 低质量的无效内卷 2 高端车规MCU产品共性 2.1 支持标定测量 2.2 低延迟通信加速 2.3 完备的网络安全解决方案 2.4虚拟化 3 国产替代的囚徒困境 1 低质量的无效内卷 近几年,车规MCU国产替代的呼声此消彼长,但仍然集中在低端产品。 从产…...
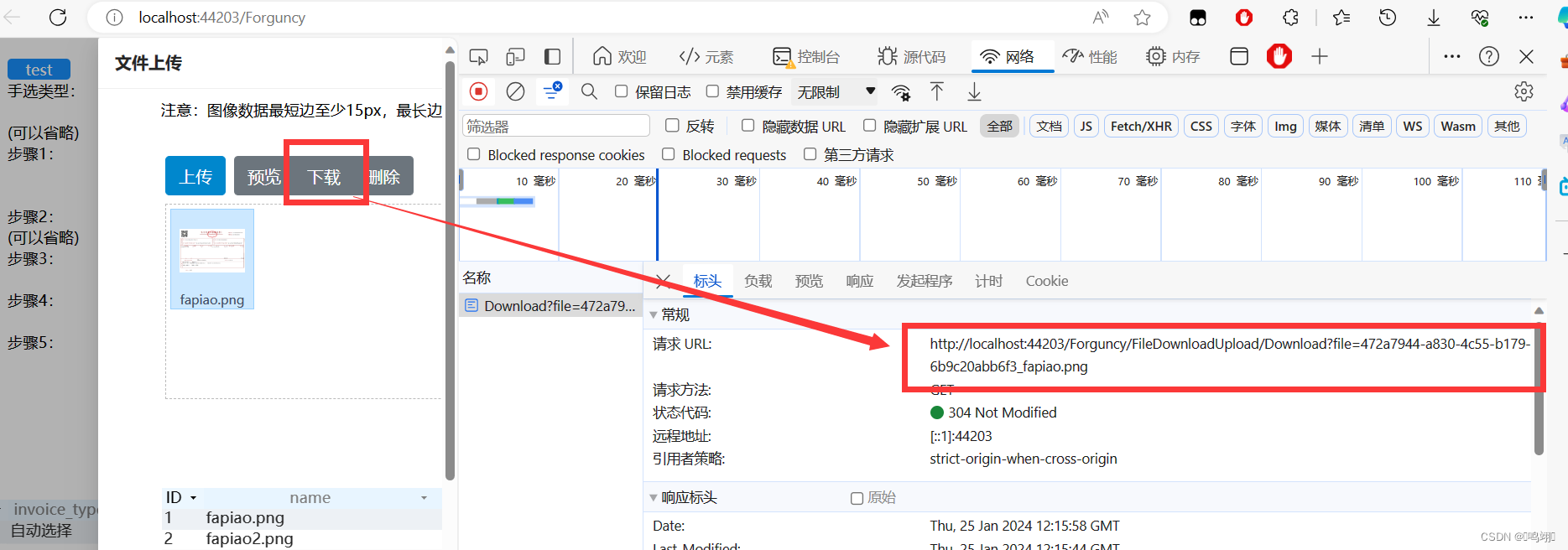
活字格V9获取图片失败bug,报错404,了解存储路径,已改为批量上传和批量获取
项目场景: 问题描述 原因分析: 解决方案: 完成了批量上传功能,这插件真的很方便 于是写了个批量获取附件的js代码,我真厉害 项目场景: 活字格V9版本获取图片链接Upload 【9.0.103.0】图片上传的存储路…...

【Echart】echart图表不显示总结
【Echart】echart图表不显示 经常遇到的场景:v-if和el-tabs切换图表不显示图表; 1、echarts.init时确认dom容器是否设置了宽高,必须设置宽高; 错误写法 <div id"line" ref"lineChart" width"100%&qu…...

vue 组件之间相互传值的6种方法
Vue.js 中组件间通信的方法有很多种,以下是6种常见的直接或间接的组件传值方式: 1. Props(父向子) 优点: 易于理解,符合单向数据流的原则,有利于代码维护。 缺点: 数据只能从父组件…...
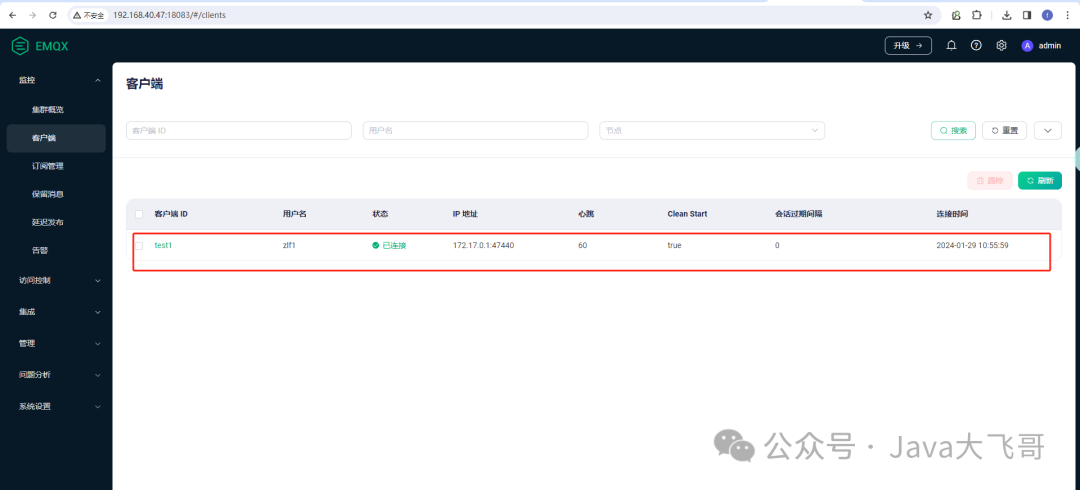
开源大规模分布式MQTT消息服务器EMQX部署教程
1.EMQX是什么? EMQX 是一款开源的大规模分布式 MQTT 消息服务器,功能丰富,专为物联网和实时通信应用而设计。EMQX 5.0 单集群支持 MQTT 并发连接数高达 1 亿条,单服务器的传输与处理吞吐量可达每秒百万级 MQTT 消息,并…...

postgresql慢查询排查和复现
postgresql慢查询排查和复现 一. 介绍一张表:pg_stat_activity pg_stat_activity 是 PostgreSQL 中一个非常有用的系统视图,提供了有关当前数据库连接和活动查询的信息。通过查询这个视图,你可以获取有关正在执行的查询、连接的用户、进程 …...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
