活字格V9获取图片失败bug,报错404,了解存储路径,已改为批量上传和批量获取
问题描述
原因分析:
解决方案:
完成了批量上传功能,这插件真的很方便
于是写了个批量获取附件的js代码,我真厉害
项目场景:
活字格V9版本获取图片链接Upload
【9.0.103.0】图片上传的存储路径和获取问题 - 活字格专区 - 求助中心 - 葡萄城开发者社区 (grapecity.com.cn)
问题描述
他们给的文档解释:
看完必恍然大悟的活字格内幕:五十五、活字格附件存储原理详解 - 活字格专区 - 专题教程 - 葡萄城开发者社区
(出处: 葡萄城开发者社区)
原因分析:
这个文档和我的情况不太一样,
他说的活字格设计时的附件存储路径是同级目录下以应用名+_fgcfiles命名的文件夹
而我的活字格设计时的附件存储路径C:\ProgramData\Forguncy\Garimi\303\WebSite\Upload\Temp
我的存储路径连应用名都没有
解决方案:
用了个插件
完成了批量上传功能,这插件真的很方便
奶奶滴,这请求路径和文档给的根本不一样好吗,我真服了
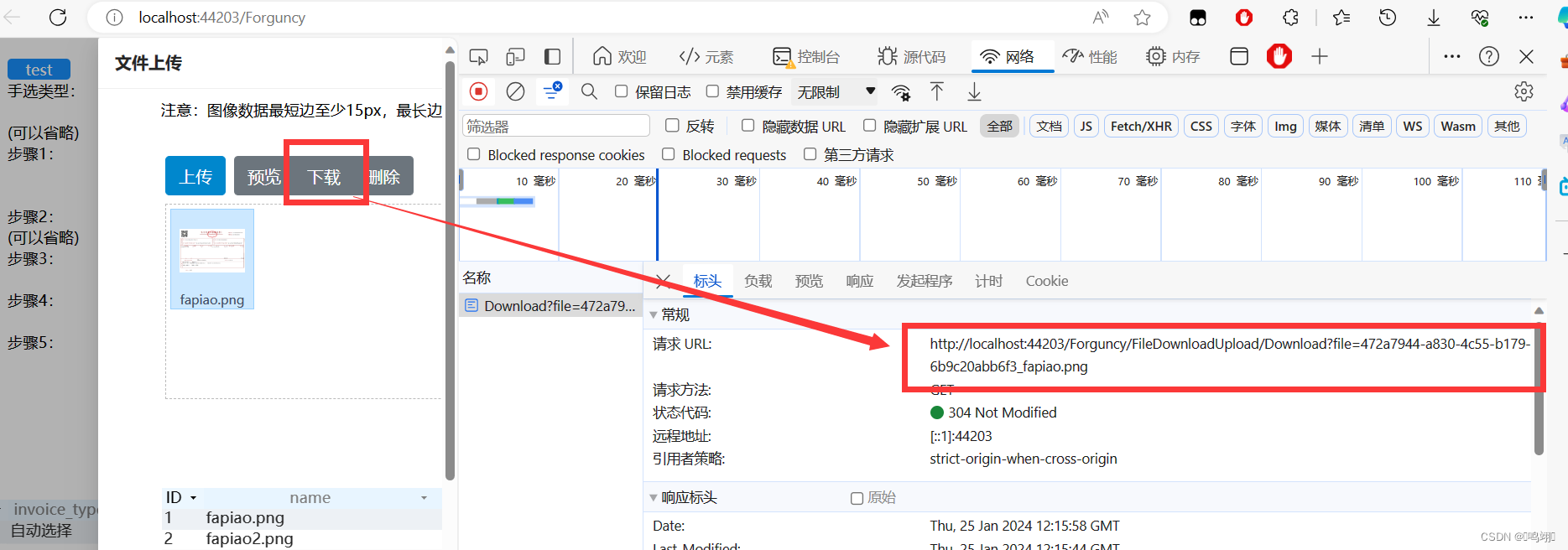
路径:http://${window.location.host}/Forguncy/FileDownloadUpload/Download?file=
于是写了个批量获取附件的js代码,我真厉害
//imgs=ffc31308-ec72-4268-a977-16f4c366a75f_whitepig.png|3e8582d5-7e4b-4544-8e51-446ba8f70905_blackpig.png
//img[1]=ffc31308-ec72-4268-a977-16f4c366a75f_whitepig.png
//img[2]=3e8582d5-7e4b-4544-8e51-446ba8f70905_blackpig.png
//....
const imgs = Forguncy.Page.getCell("img").getValue();
const imgArray = imgs.split("|");
//遍历imgArray
for (let i = 0; i < imgArray.length; i++) {(function(index) {var img = `http://${window.location.host}/Forguncy/FileDownloadUpload/Download?file=` + imgArray[index];var image = new Image();var base64;image.src = img;console.log("第" + index + "轮次的src:" + image.src);image.onload = function () {base64 = getBase64Image(image);console.log(index + base64);Forguncy.modifyTablesData({image: {addRows: [{name: getImgName(imgArray[index]),code: imgArray[index],base64: base64,is_identify: false}],}});}})(i);
}function getBase64Image(img) {var canvas = document.createElement("canvas");canvas.width = img.width;canvas.height = img.height;var ctx = canvas.getContext("2d");ctx.drawImage(img, 0, 0, img.width, img.height);var ext = img.src.substring(img.src.lastIndexOf(".") + 1).toLowerCase();var dataURL = canvas.toDataURL("image/" + ext);return dataURL;
}function getImgName(input) {var match = input.match(/_([^_]*)(?:\.|$)/);var result = match && match[1];return result || null;
}
相关文章:

活字格V9获取图片失败bug,报错404,了解存储路径,已改为批量上传和批量获取
项目场景: 问题描述 原因分析: 解决方案: 完成了批量上传功能,这插件真的很方便 于是写了个批量获取附件的js代码,我真厉害 项目场景: 活字格V9版本获取图片链接Upload 【9.0.103.0】图片上传的存储路…...

【Echart】echart图表不显示总结
【Echart】echart图表不显示 经常遇到的场景:v-if和el-tabs切换图表不显示图表; 1、echarts.init时确认dom容器是否设置了宽高,必须设置宽高; 错误写法 <div id"line" ref"lineChart" width"100%&qu…...

vue 组件之间相互传值的6种方法
Vue.js 中组件间通信的方法有很多种,以下是6种常见的直接或间接的组件传值方式: 1. Props(父向子) 优点: 易于理解,符合单向数据流的原则,有利于代码维护。 缺点: 数据只能从父组件…...
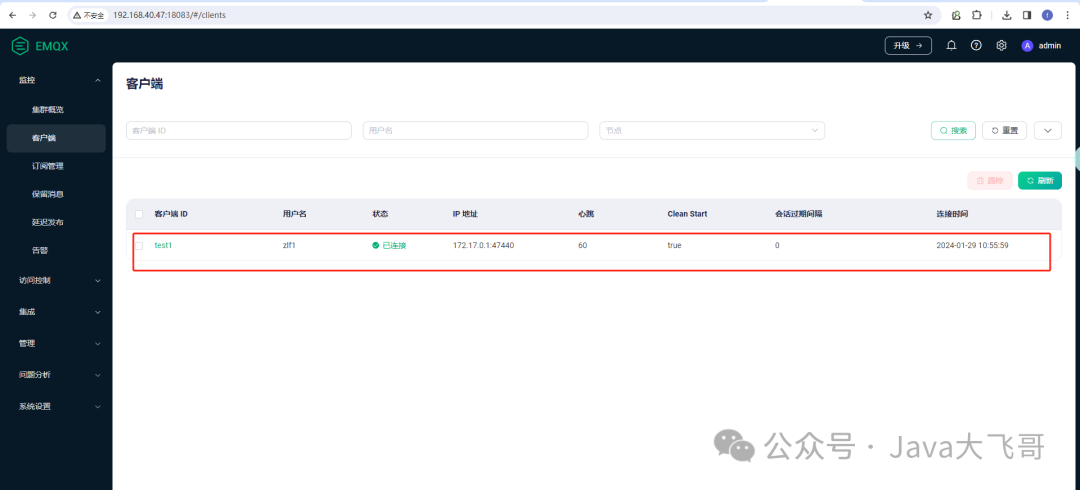
开源大规模分布式MQTT消息服务器EMQX部署教程
1.EMQX是什么? EMQX 是一款开源的大规模分布式 MQTT 消息服务器,功能丰富,专为物联网和实时通信应用而设计。EMQX 5.0 单集群支持 MQTT 并发连接数高达 1 亿条,单服务器的传输与处理吞吐量可达每秒百万级 MQTT 消息,并…...

postgresql慢查询排查和复现
postgresql慢查询排查和复现 一. 介绍一张表:pg_stat_activity pg_stat_activity 是 PostgreSQL 中一个非常有用的系统视图,提供了有关当前数据库连接和活动查询的信息。通过查询这个视图,你可以获取有关正在执行的查询、连接的用户、进程 …...

【服务器】搭建ChatGPT站点常见问题
目录 ❓ 常见问题 🌼1. 什么是OpenAI APIkey? 🌼2. 什么是Token? 🌼3. 为什么回复不是GPT-4? 🌼4. 如何区分 GPT-3.5 和 GPT-4 🌼5. 为什么回复到一半卡住? 🌼6.…...

QT+opengl 创建一个六边形
一.关键名词解释 VAO: Vertex Array Object, 顶点数组对象,你要绘制的图形。 VBO:Vertex Buffer Object, 顶点缓冲对象,所有顶点的集合。 EBO:Element Buffer Object, 元素缓冲对象,顶点的索引值。 IBO: Index Buffer Object, 索引缓冲对象。…...
 引发的卡顿问题)
Android imageView.setImageXXX() 引发的卡顿问题
在 Android 开发中,ImageView 是一个用户界面控件,用于在应用中显示图片。它是 Android UI 组件库中一个非常基础和常用的部分。使用 ImageView,你可以在屏幕上显示来自不同来源的图像,比如位图文件、绘图资源 drawable、网络来源…...

MavenGradle等引入jSerialComm
引入 jSerialComm [2.0.0,3.0.0) 此版本发布于 Nov 7, 2023 (23年11月) Maven: <dependency><groupId>com.fazecast</groupId><artifactId>jSerialComm</artifactId><version>[2.0.0,3.0.0)</version> </dependency>Ivy: …...

热门技术问答 | 请 GaussDB 用户查收
近年来,Navicat 与华为云 GaussDB 展开一系列技术合作,为 GaussDB 用户提供面向管理开发工具的生态工具。Navicat 现已完成 GaussDB 主备版(单节点、多节点)和分布式数据库的多项技术对接。Navicat 通过工具的流畅性和实用性&…...
【C/C++ 01】初级排序算法
排序算法通常是针对数组或链表进行排序,在C语言中,需要手写排序算法完成对数据的排序,排序规则通常为升序或降序(本文默认为升序),在C中,<algorithm>头文件中已经封装了基于快排算法的 st…...

Android Settings 显示电池点亮百分比
如题,Android 原生 Settings 里有个 电池电量百分比 的选项,打开后电池电量百分比会显示在状态栏。 基于 Android 13 , 代码在 ./packages/apps/Settings/src/com/android/settings/display/BatteryPercentagePreferenceController.java &am…...
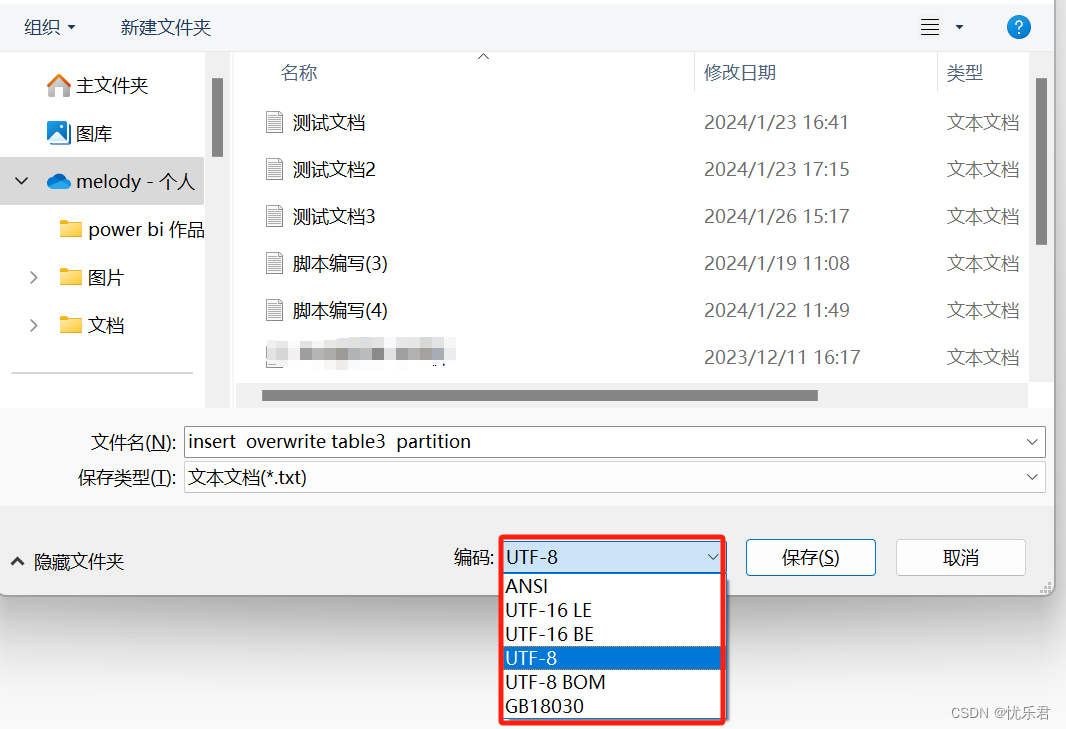
Windows记事本不显示下划线的原因及解决方法
最近使用Windows 记事本敲代码发现一个问题:代码中的下划线无法显示!!!(字体为“微软雅黑”、字体大小为11下,代码中的下划线无法显示。当然每个人情况可能不同) 在 Windows 记事本中,下划线可能会因为 字体…...
(四十六))
嵌入式软件工程师面试题——2025校招社招通用(C/C++)(四十六)
说明: 面试群,群号: 228447240面试题来源于网络书籍,公司题目以及博主原创或修改(题目大部分来源于各种公司);文中很多题目,或许大家直接编译器写完,1分钟就出结果了。但…...
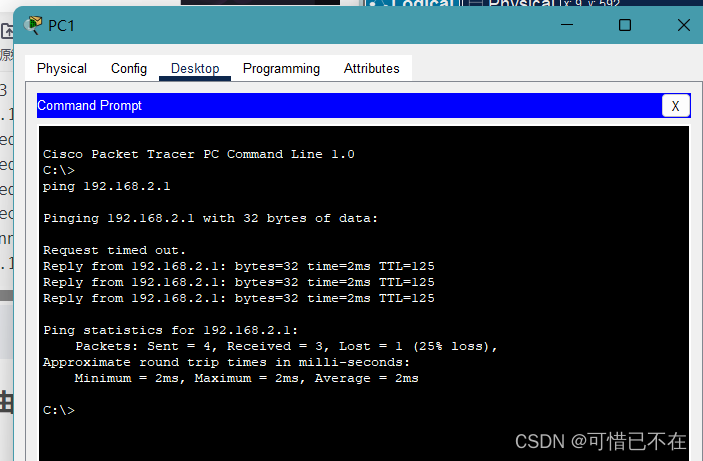
【学网攻】 第(13)节 -- 动态路由(OSPF)
系列文章目录 目录 系列文章目录 文章目录 前言 一、动态路由是什么? 二、实验 1.引入 实验拓扑图 实验配置 实验验证 总结 文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻】 第(2)节 -- 交换机认识及使用【学网攻】 第(3)节 -- 交换机配置聚合端口【学…...

Asp.Net Core 获取应用程序相关目录
在ASP.NET Core中,可以通过以下三种方式获取应用程序所在目录: 1、使用AppContext.BaseDirectory属性: string appDirectory AppContext.BaseDirectory; 例如:D:\后端项目\testCore\test.WebApi\bin\Debug\net6.0\ 2、使用…...
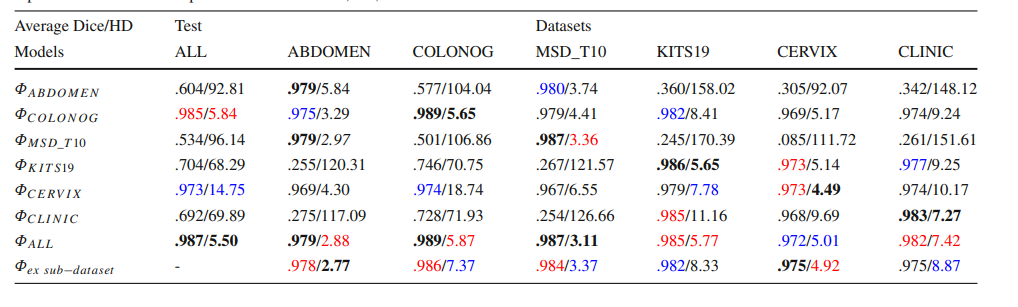
文献速递:人工智能医学影像分割--- 深度学习分割骨盆骨骼:大规模CT数据集和基线模型
文献速递:人工智能医学影像分割— 深度学习分割骨盆骨骼:大规模CT数据集和基线模型 我们为大家带来人工智能技术在医学影像分割上的应用文献。 人工智能在医学影像分析中发挥着至关重要的作用,尤其体现在图像分割技术上。这项技术的目的是准…...
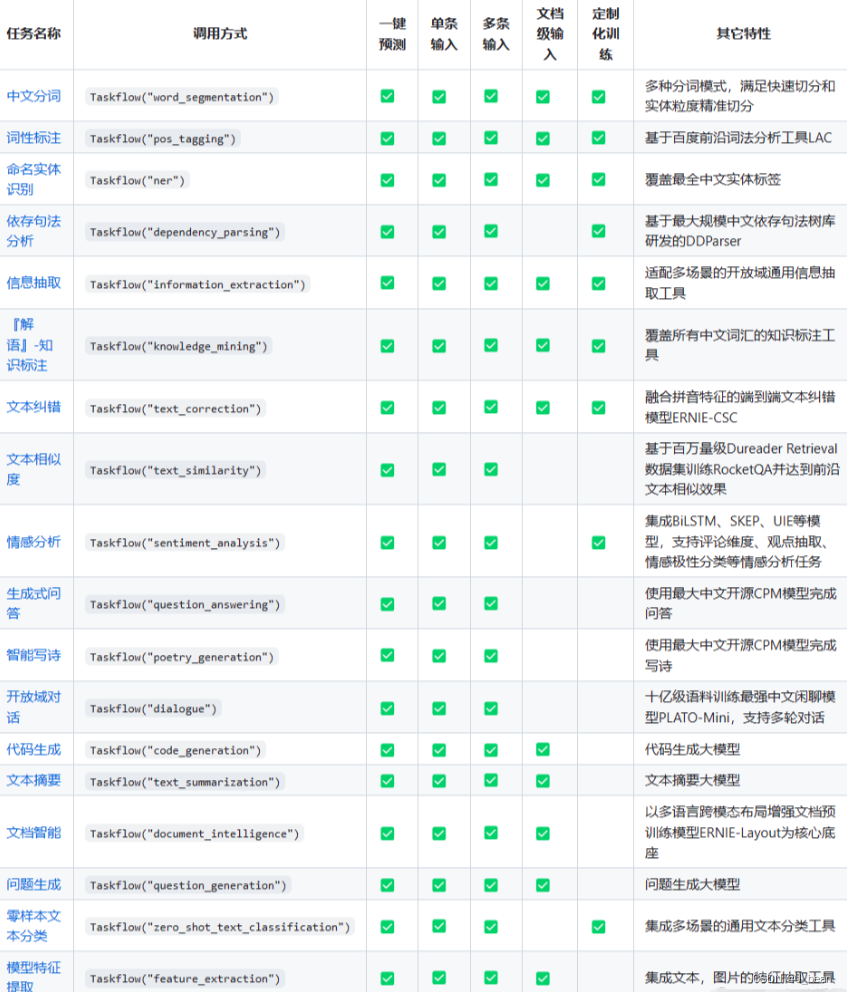
PaddleNLP的简单使用
1 介绍 PaddleNLP是一个基于PaddlePaddle深度学习平台的自然语言处理(NLP)工具库。 它提供了一系列用于文本处理、文本分类、情感分析、文本生成等任务的预训练模型、模型组件和工具函数。 PaddleNLP有统一的应用范式:通过 paddlenlp.Task…...
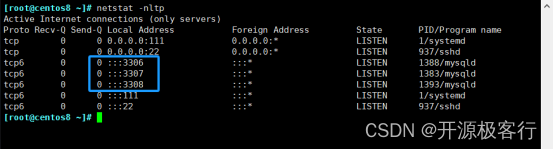
2. MySQL 多实例
重点: MySQL 的 三种安装方式:包安装,二进制安装,源码编译安装。 MySQL 的 基本使用 MySQL 多实例 DDLcreate alter drop DML insert update delete DQL select 2.5)通用 二进制格式安装 MySQL 2.5.1ÿ…...

两个五层决策树和一个十层决策树的区别
随机森林的弹性: 随机森林中的多个决策树是相互独立构建的,因此两个五层决策树和一个十层决策树之间的区别可能在于它们对训练数据的不同学习。这种弹性有助于模型更好地适应不同的数据模式。 过拟合风险: 十层决策树可能更容易过拟合训练数据,尤其是在数…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

