Good Trip Codeforces Round 921 (Div. 2) 1925D
Problem - D - Codeforces
题目大意:有n个数,其中有m个匹配对,对于一个匹配对(x,y),他们的除湿贡献为z,一共有k轮行动,每一轮从n个数中独立等概率的选出两个数,如果这两个数在一个匹配对内,那么就贡献z的分数,同时z永远+1,如果不在匹配对立就贡献0,问最终分数的期望是多少
2<=n<=1e5;0<=m<=min(1e5,n*(n-1)/2);1<=k<=2e5
思路:因为只有匹配对被选中才有贡献,所以很容易想到可以枚举每个匹配对,然后枚举其被选中的次数,被选中的次数符合二项分布,但这样两层循环枚举显然会超时。
因为每一对被选中的概率都是一样的,只有初始贡献不同,所以如果我们把每个匹配对的初始贡献的期望都算出来,这样就可以把所有匹配对看做m个初始贡献为0的匹配对,只需要枚举被选中的次数然后乘以m即可。
考虑怎么算初始贡献的期望,每个匹配对被选中的概率psel=1/C(2,n),k轮中被选中的次数的期望就是k/C(2,n),再乘以贡献z,z*k/C(2,n)就是单个匹配对初始贡献的期望,可以O(m)的时间求出。
然后从2到k枚举每个匹配对被选中的次数i,被选中i次的累计贡献为(0+i-1)*i/2,因为每次被选中的概率psel独立等概符合二项分布,所以被选中i次的概率为C(i,k)*(psel)的i次方*(1-psel)的k-i次方,再乘以m,将所有贡献相加,注意预处理逆元和取模即可。
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
typedef long long ll;
const ll MOD = 1e9 + 7;
ll n;
ll fac[N];
ll inv[N];
ll qpow(ll a, ll b)
{//快速幂a %= MOD;ll ret = 1;while (b){if (b & 1){ret = ret * a % MOD;}a = a * a % MOD;b >>= 1;}return ret;
}
ll C(ll x, ll y)
{//组合数的O(1)算法return inv[x] * fac[y] %MOD * inv[y - x] % MOD;
}
void initfac()
{//预处理阶乘和逆元fac[0] = inv[0] = 1;for (int i = 1; i <= 200000; i++){fac[i] = fac[i - 1] * i % MOD;inv[i] = qpow(fac[i], MOD - 2);}
}
void init()
{}
void solve()
{cin >> n;init();ll m;cin >> m;ll k;cin >> k;ll ans = 0;ll psel = qpow(C(2, n), MOD - 2);//每个匹配对被选中的概率for (int i = 1; i <= m; i++){ll x, y, z;cin >> x >> y >> z;ans = (ans + k * psel % MOD * z % MOD) % MOD;//算出每个匹配对的除湿贡献产生的期望}for (ll i = 2; i <= k; i++){//枚举每个匹配对被选中的次数ll con = i * (i - 1) % MOD * qpow(2, MOD - 2) % MOD;//被选中i次的总贡献ll pro = C(i, k) * qpow(psel, i) % MOD * qpow((1-psel+MOD)%MOD, k - i) % MOD;//被选中i次的概率ans = (ans + con * pro % MOD * m % MOD) % MOD;}cout << ans;cout << '\n';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);int t;cin >> t;initfac();while (t--){solve();}return 0;
}相关文章:
 1925D)
Good Trip Codeforces Round 921 (Div. 2) 1925D
Problem - D - Codeforces 题目大意:有n个数,其中有m个匹配对,对于一个匹配对(x,y),他们的除湿贡献为z,一共有k轮行动,每一轮从n个数中独立等概率的选出两个数,如果这两…...
推荐一款Linux、数据库、Redis、MongoDB统一管理平台!
官方演示 状态查看 ssh 终端 文件操作 数据库操作 sql 编辑器 在线增删改查数据 Redis 操作 Mongo 操作 系统管理 账号管理 角色管理 资源管理 一.安装 1.下载安装包 cd /opt wget https://gitee.com/dromara/mayfly-go/releases/download/v1.7.1/mayfly-go-linux-amd64.zi…...
TensorFlow2实战-系列教程6:迁移学习实战
🧡💛💚TensorFlow2实战-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Jupyter Notebook中进行 本篇文章配套的代码资源已经上传 1、迁移学习 用已经训练好模型的权重参数当做自己任务的模型权重初始化一般全连接层需…...

怎样开发adobe indesign插件,具体流程?
文章目录 第一.流程步骤第二.如何调试indesign插件第三.相关资源第四.总结 第一.流程步骤 开发Adobe InDesign插件通常涉及以下步骤: 获取SDK和工具: 从Adobe官方网站下载最新的Adobe InDesign SDK(Software Development Kit)&am…...

Docker 安装与基本操作
目录 一、Docker 概述 1、Docker 简述 2、Docker 的优势 3、Docker与虚拟机的区别 4、Docker 的核心概念 1)镜像 2)容器 3)仓库 二、Docker 安装 1、命令: 2、实操: 三、Docker 镜像操作 1、命令࿱…...

译文带你理解Python的dataclass装饰器
dataclass 是 Python dataclasses 模块中的一个 decorator。当使用 dataclass 装饰器时,它会自动生成一些特殊方法,包括: _ _ init _ _:用于初始化字段的构造函数_ _ repr _ _:对象的字符串表示_ _ eq _ _:…...

【C语言】实现程序的暂停
编写程序时,有时候需要让程序在某些地方暂停执行,等待用户输入或者观察程序执行结果。在 C 语言中,有多种方法可以实现程序的暂停,包括 system("pause")、getchar() 和 while ((c getchar()) ! \n && c ! EOF)…...

Hana SQL+正则表达式
目录 一、Pre 前言 二、知识点拆解 1)case when…then…else 2)json_value 函数 拓展资料 3)CAST 函数 拓展资料 4) ROUND 函数 5)occurences_regexpr 函数 拓展资料 6)正则表达式 拓展资料 三、整合分析…...

【笔记】顺利通过EMC试验(16-41)-视频笔记
目录 视频链接 P1:电子设备中有哪些主要骚扰源 P2:怎样减小DC模块的骚扰 P3:PCB上的辐射源究竟在哪里 P4:怎样控制PCB板的电磁辐射 P5:多层线路板是解决电磁兼容问题的简单方法 P6:怎样处理地线上的裂缝 P7:怎样降低时钟信号的辐射 P8:为什么IO接口的处理特别重要 P9…...
Qlik Sense 调用NPrinting生成On-Demand报表
安装 Qlik Sense On-Demand 报表控件 On-Demand 报表控件添加按钮,该按钮按需生成 Qlik NPrinting 报表。它包括在 Dashboard bundle 中。 当您希望用户能够使用应用程序中的选择作为过滤器在 Qlik Sense 中打印预定义 Qlik NPrinting 报表时,On-Deman…...
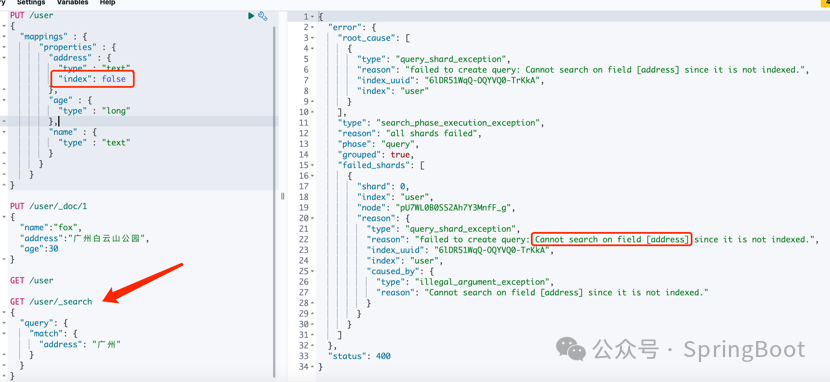
ElasticSearch重建/创建/删除索引操作 - 第501篇
历史文章(文章累计500) 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 E…...

数据写入HBase(scala)
package sourceimport org.apache.hadoop.hbase.{HBaseConfiguration, TableName} import org.apache.hadoop.hbase.client.{ConnectionFactory, Put} import org.apache.hadoop.hbase.util.Bytesobject ffff {def main(args: Array[String]): Unit {//hbase连接配置val conf …...
Codeforces Round 799 (Div. 4)
目录 A. Marathon B. All Distinct C. Where’s the Bishop? D. The Clock E. Binary Deque F. 3SUM G. 2^Sort H. Gambling A. Marathon 直接模拟 void solve() {int ans0;for(int i1;i<4;i) {cin>>a[i];if(i>1&&a[i]>a[1]) ans;}cout<&l…...

为什么要用云手机养tiktok账号
在拓展海外电商市场的过程中,许多用户选择采用tiktok短视频平台引流的策略,以提升在电商平台上的流量,吸引更多消费者。而要进行tiktok引流,养号是必不可少的一个环节。tiktok云手机成为实现国内跨境养号的一种有效方式࿰…...

vue pc端网页实现自适应
一、基本原理 pc端做自适应可以用rem来实现,啥是rem,自己百度 二、新建rem.ts文件 // rem等比适配配置文件 // 基准大小 const baseSize 14 // 设置 rem 函数 function setRem () {// 当前页面宽度相对于 1920宽的缩放比例,可根据自己需要…...
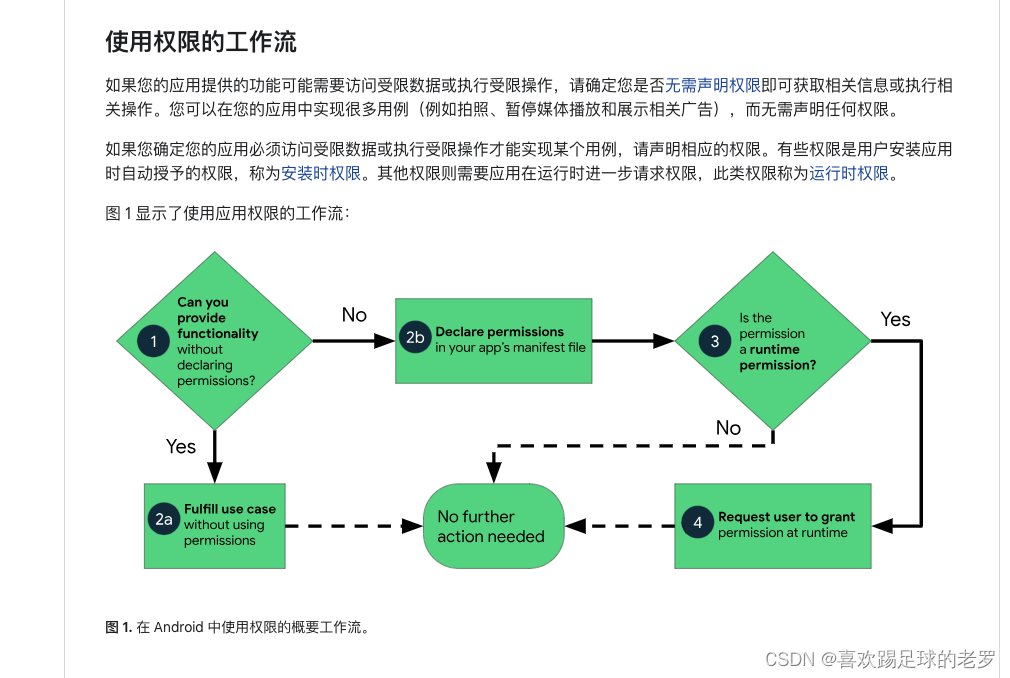
Android 13以上版本读写SD卡权限适配
如题,最近工作上处理的问题,把解决方案简单逻列出来,供有需要的朋友参考之 解决方案: 1、配置权限 <uses-permission android:name"android.permission.READ_MEDIA_IMAGES" /><uses-permission android:name&q…...

并查集模板:食物链详解
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader;public class Main {static int N 50010;static int n,m; //n个动物,m局判断static int[] p new int[N]; //p[i]是i的根节点static int[] d new int[N]; //d[i]表示i到…...

使用WAF防御网络上的隐蔽威胁之反序列化攻击
什么是反序列化 反序列化是将数据结构或对象状态从某种格式转换回对象的过程。这种格式通常是二进制流或者字符串(如JSON、XML),它是对象序列化(即对象转换为可存储或可传输格式)的逆过程。 反序列化的安全风险 反…...
05. 交换机的基本配置
文章目录 一. 初识交换机1.1. 交换机的概述1.2. Ethernet_ll格式1.3. MAC分类1.4. 冲突域1.5. 广播域1.6. 交换机的原理1.7. 交换机的3种转发行为 二. 初识ARP2.1. ARP概述2.2. ARP报文格式2.3. ARP的分类2.4. 免费ARP的作用 三. 实验专题3.1. 实验1:交换机的基本原…...

yolo将标签数据打到原图上形成目标框
第一章 目标:为了查看自己在标注标签时是否准确,写了这段代码来将标注的框打到原图上 第二章 步骤:进行反归一化得到坐标画出矩形框 第二行是目标图片对应的txt,第三行是目标图片 第三章 全部代码如下: import cv2 import …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
