Codeforces Round 799 (Div. 4)
目录
A. Marathon
B. All Distinct
C. Where’s the Bishop?
D. The Clock
E. Binary Deque
F. 3SUM
G. 2^Sort
H. Gambling
A. Marathon
直接模拟
void solve()
{int ans=0;for(int i=1;i<=4;i++) {cin>>a[i];if(i>1&&a[i]>a[1]) ans++;}cout<<ans<<endl;return ;
}B. All Distinct
把重复的数删除然后判断是不是删的偶数个不是就再减去一个即可
void solve()
{cin>>n;vector<int> a;for(int i=1;i<=n;i++){int x; cin>>x;a.push_back(x);}sort(a.begin(),a.end());a.erase(unique(a.begin(),a.end()),a.end());int now=n-a.size();cout<<(now%2==0 ? a.size() : a.size()-1)<<endl;return ;
}C. Where’s the Bishop?
简单的八皇后行列的性质,也就是副对角线的是行列之和相等,主对角线是差值相等需要加上n防止越界,接着谁所在的行列之和最大谁就是king
char a[M][M];
int d[M],ud[M];
void solve()
{n=m=8;memset(d,0,sizeof d);memset(ud,0,sizeof ud);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]=='#'){d[i+j]++;ud[8-i+j]++;}}}int x=0,y=0,ma=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(d[i+j]+ud[8-i+j]>ma){ma=d[i+j]+ud[8-i+j];x=i,y=j;}}}cout<<x<<" "<<y<<endl;return ;D. The Clock
简单模拟即可,我们发现这一类题目都是数据范围很小 我们可以先装为总的分钟再来变化即可用mp记录是否出现过
map<PII,int> mp;
void solve()
{string s; cin>>s>>m;h=(s[0]-'0')*10+s[1]-'0';n=(s[3]-'0')*10+s[4]-'0';mp.clear();int hh=m/60,mm=m-hh*60;int ans=0;while(1){if(mp[{h,n}]) break;mp[{h,n}]++;string x,y;int xx=h,yy=n;while(xx){x+=xx%10+'0';xx/=10;}while(yy){y+=yy%10+'0';yy/=10;}if(h<10) x+='0';if(n<10) y+='0';reverse(x.begin(),x.end());if(x==y) ans++;h+=hh,n+=mm;if(n>=60) n-=60,h++;if(h>=24) h-=24;}cout<<ans<<endl;return ;
}E. Binary Deque
简单性质使用 要删除的最少也就是留下的最多我们可以考虑使用双指针,如果后面多了一定要删去前面的
void solve()
{cin>>n>>m;int sum=0;for(int i=1;i<=n;i++) cin>>a[i],sum+=a[i];if(sum<m) cout<<-1<<endl;else{sum=0;int ans=0;for(int i=1,j=1;i<=n;i++){sum+=a[i];while(sum>m){sum-=a[j];j++;}if(sum==m) ans=max(ans,i-j+1);}cout<<n-ans<<endl;}return ;
}F. 3SUM
考虑到我们只需要看最后一个位置所以我们只需要把每一个数的最后一位取出来即可然后直接
暴力即可
int a[10];
void solve()
{cin>>n;memset(a,0,sizeof a);for(int i=1;i<=n;i++){int x; cin>>x;a[x%10]++;}for(int i=0;i<=9;i++){for(int j=0;j<=9;j++){for(int k=0;k<=9;k++){if(i==j&&j==k&&a[i]<3) continue;if(i==j&&a[i]<2) continue;if(i==k&&a[i]<2) continue;if(j==k&&a[j]<2) continue;if(!a[i]||!a[j]||!a[k]) continue;if((i+j+k)%10==3){cout<<"YES"<<endl;return ;}}}}cout<<"NO"<<endl;return ;
}G. 2^Sort
我们发现变化的其实之后后面一个数多乘以2了后面也是一样的就判断 是否满足即可如果不满足重新开始,双指针算法
int a[N];
void solve()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];int ans=0,len=1;for(int i=2;i<=n;i++){if(a[i]*2>a[i-1]) len++;else{if(len>m) ans+=len-m;len=1;}} if(len>m) ans+=len-m;cout<<ans<<endl;return ;
}H. Gambling
我们发现其实只需要对每一个数来判断即可我们也就是求一个数的区间的数量减去其他数的数量,
我们可以把这个数看成1,其它的数就是-1来计算贡献来维护一个前缀最小的即可
void solve()
{cin>>n;map<int,set<PII>> mp;int res=0,a=0,l=0,r=0;for(int i=1;i<=n;i++){int x; cin>>x;int sum=2*mp[x].size()-i;mp[x].insert({sum-1,i});// auto it=*mp[x].begin();if(sum-it.first>res){res=sum-it.first;a=x;l=it.second;r=i;}}cout<<a<<" "<<l<<" "<<r<<endl;
}相关文章:
Codeforces Round 799 (Div. 4)
目录 A. Marathon B. All Distinct C. Where’s the Bishop? D. The Clock E. Binary Deque F. 3SUM G. 2^Sort H. Gambling A. Marathon 直接模拟 void solve() {int ans0;for(int i1;i<4;i) {cin>>a[i];if(i>1&&a[i]>a[1]) ans;}cout<&l…...

为什么要用云手机养tiktok账号
在拓展海外电商市场的过程中,许多用户选择采用tiktok短视频平台引流的策略,以提升在电商平台上的流量,吸引更多消费者。而要进行tiktok引流,养号是必不可少的一个环节。tiktok云手机成为实现国内跨境养号的一种有效方式࿰…...

vue pc端网页实现自适应
一、基本原理 pc端做自适应可以用rem来实现,啥是rem,自己百度 二、新建rem.ts文件 // rem等比适配配置文件 // 基准大小 const baseSize 14 // 设置 rem 函数 function setRem () {// 当前页面宽度相对于 1920宽的缩放比例,可根据自己需要…...
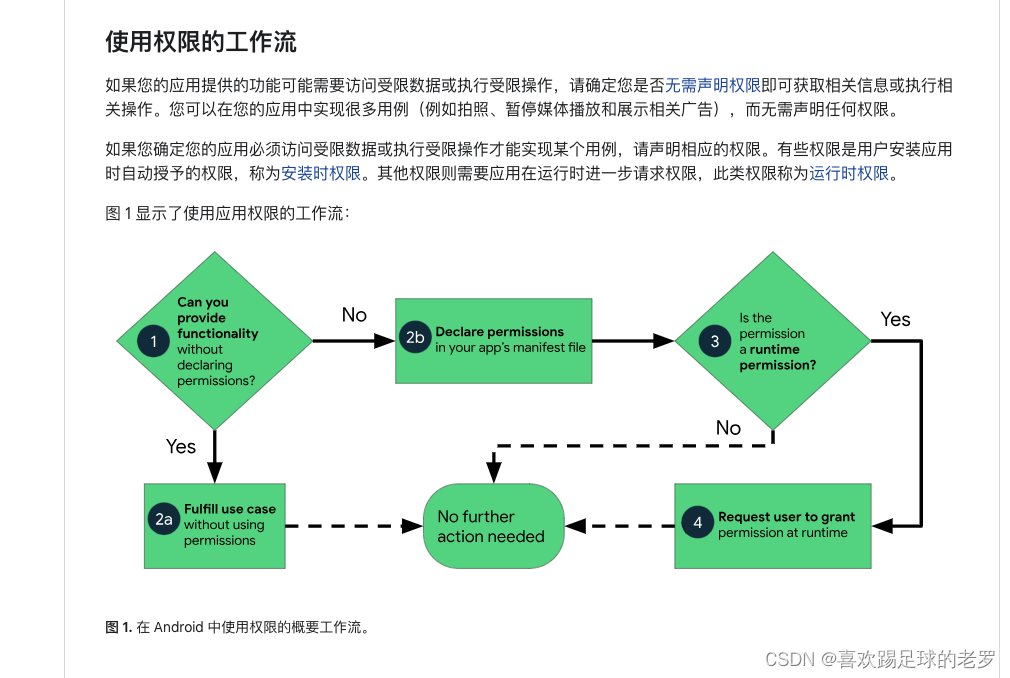
Android 13以上版本读写SD卡权限适配
如题,最近工作上处理的问题,把解决方案简单逻列出来,供有需要的朋友参考之 解决方案: 1、配置权限 <uses-permission android:name"android.permission.READ_MEDIA_IMAGES" /><uses-permission android:name&q…...

并查集模板:食物链详解
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader;public class Main {static int N 50010;static int n,m; //n个动物,m局判断static int[] p new int[N]; //p[i]是i的根节点static int[] d new int[N]; //d[i]表示i到…...

使用WAF防御网络上的隐蔽威胁之反序列化攻击
什么是反序列化 反序列化是将数据结构或对象状态从某种格式转换回对象的过程。这种格式通常是二进制流或者字符串(如JSON、XML),它是对象序列化(即对象转换为可存储或可传输格式)的逆过程。 反序列化的安全风险 反…...
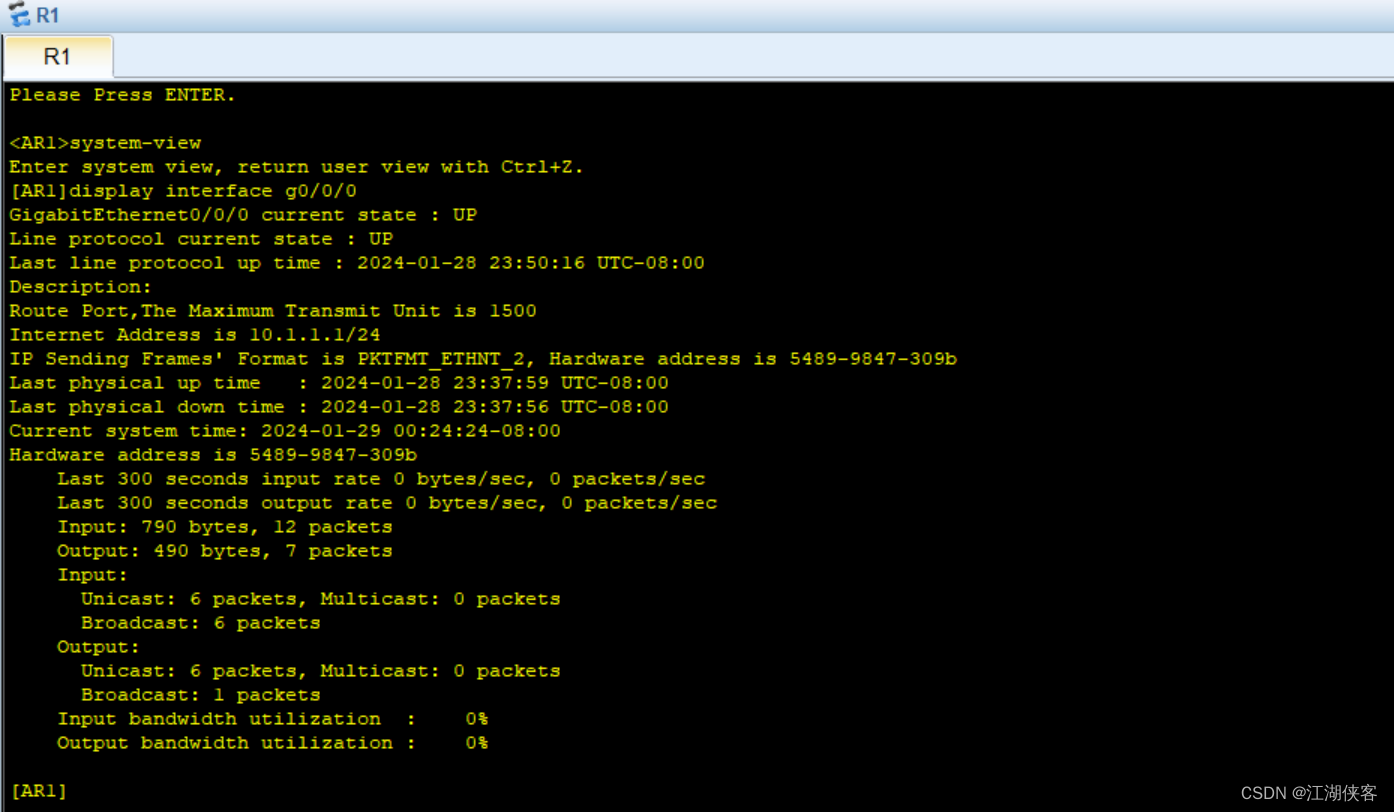
05. 交换机的基本配置
文章目录 一. 初识交换机1.1. 交换机的概述1.2. Ethernet_ll格式1.3. MAC分类1.4. 冲突域1.5. 广播域1.6. 交换机的原理1.7. 交换机的3种转发行为 二. 初识ARP2.1. ARP概述2.2. ARP报文格式2.3. ARP的分类2.4. 免费ARP的作用 三. 实验专题3.1. 实验1:交换机的基本原…...

yolo将标签数据打到原图上形成目标框
第一章 目标:为了查看自己在标注标签时是否准确,写了这段代码来将标注的框打到原图上 第二章 步骤:进行反归一化得到坐标画出矩形框 第二行是目标图片对应的txt,第三行是目标图片 第三章 全部代码如下: import cv2 import …...

002-00-02【大红ai源码】dolphinscheduler3.2.0 源码环境搭建------by孤山村头王大爷家女儿大红
【ai阅读源码-dolphinscheduler】 DolphinScheduler 开发手册1、软件要求2、克隆代码库3、编译打包4、代码风格5、新建数据库,导入元数据。6, 启动后端6.1 启动api-server 6.2 启动master-server6.3 启动worker-server 7 启动前端 DolphinScheduler 开发…...

python-自动化篇-运维-监控-如何使⽤Python处理和解析⽇志⽂件?-实操记录
文章目录 1. 选择日志文件格式: 确定要处理的日志文件的格式。不同的日志文件可能具有不同的格式,如文本日志、CSV、JSON、XML等。了解日志文件的格式对解析⾮常重要。2. 打开日志文件: 使⽤Python的文件操作功能打开日志文件,以便…...
代码随想录算法训练营DAY6 | 哈希表(1)
DAY5休息一天,今天重启~ 哈希表理论基础:代码随想录 Java hash实现 :java 哈希表-CSDN博客 一、LeetCode 242 有效的字母异位词 题目链接:242.有效的字母异位词 思路:设置字典 class Solution {public boolean isAnag…...
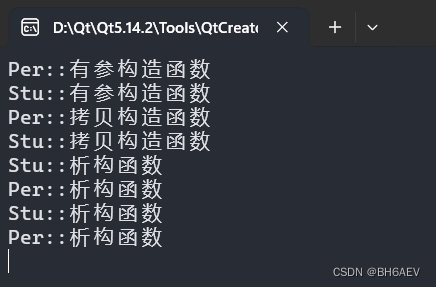
【嵌入式学习】C++QT-Day3-C++基础
笔记 见我的博客:https://lingjun.life/wiki/EmbeddedNote/19Cpp 作业 设计一个Per类,类中包含私有成员:姓名、年龄、指针成员身高、体重,再设计一个Stu类,类中包含私有成员:成绩、Per类对象p1,设计这两个类的构造函…...
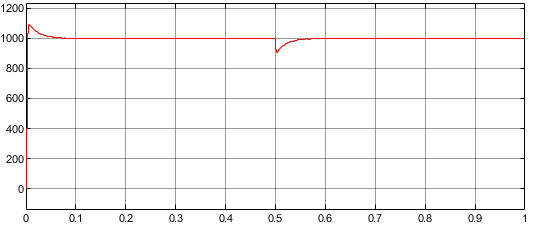
表贴式PMSM的直接转矩控制(DTC)MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 模型简介 表贴式PMSM的直接转矩控制(DTC),直接使用滞环控制对转矩和磁链进行控制,相对于传统的FOC控制而言,其不需要进行解耦变换,在此次的有以下几点需要注意:…...

详解OpenHarmony各部分文件在XR806上的编译顺序
大家好,今天我们来谈一谈编程时一个很有趣的话题——编译顺序。我知道,一提到编译可能大家会感到有点儿头疼,但请放心,我不会让大家头疼的。我们要明白,在开始写代码之前,了解整个程序的编译路径是十分有必…...

【美团】无人机-大数据开发工程师
更新时间:2024/01/29 工作地点:北京市 事业群:到家事业群 工作经验:3年 部门介绍 为了更好地提升城市即时配送的效率与体验,美团于2017年启动了无人机配送服务的探索,通过科技创新推动履约工具变革&#x…...

微服务系统设计:横向扩展和纵向扩展的对比
微服务扩展性:水平扩展 vs 垂直扩展 特点水平扩展垂直扩展扩展单位增加微服务实例增加单个实例的资源 (CPU,内存)方向向外,增加节点向上,增加单个节点的资源复杂性随着实例数量的增加,管理难度更大管理更简单…...

Java基于SpringBoot+Vue的网上超市管理系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
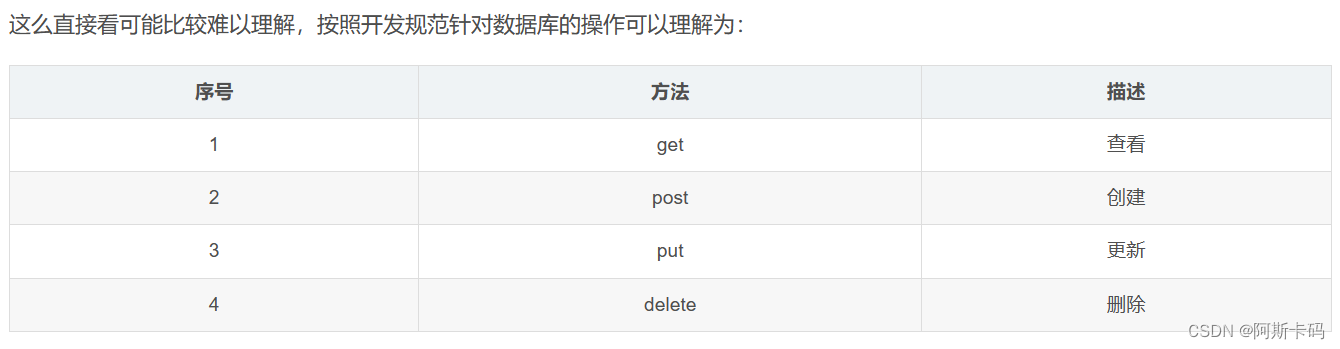
HTTP中POST、GET、PUT、DELETE方式的区别
GET请求会向数据库发索取数据的请求,从而来获取信息,该请求就像数据库的select操作一样,只是用来查询一下数据,不会修改、增加数据,不会影响资源的内容,即该请求不会产生副作用。无论进行多少次操作&#x…...

77.Go中interface{}判nil的正确姿势
文章目录 一:interface{}简介二、interface{}判空三:注意点四:实际案例 一:interface{}简介 在go中的nil只能赋值给指针、channel、func、interface、map或slice类型的变量 interface 是否根据是否包含有 method,底层…...
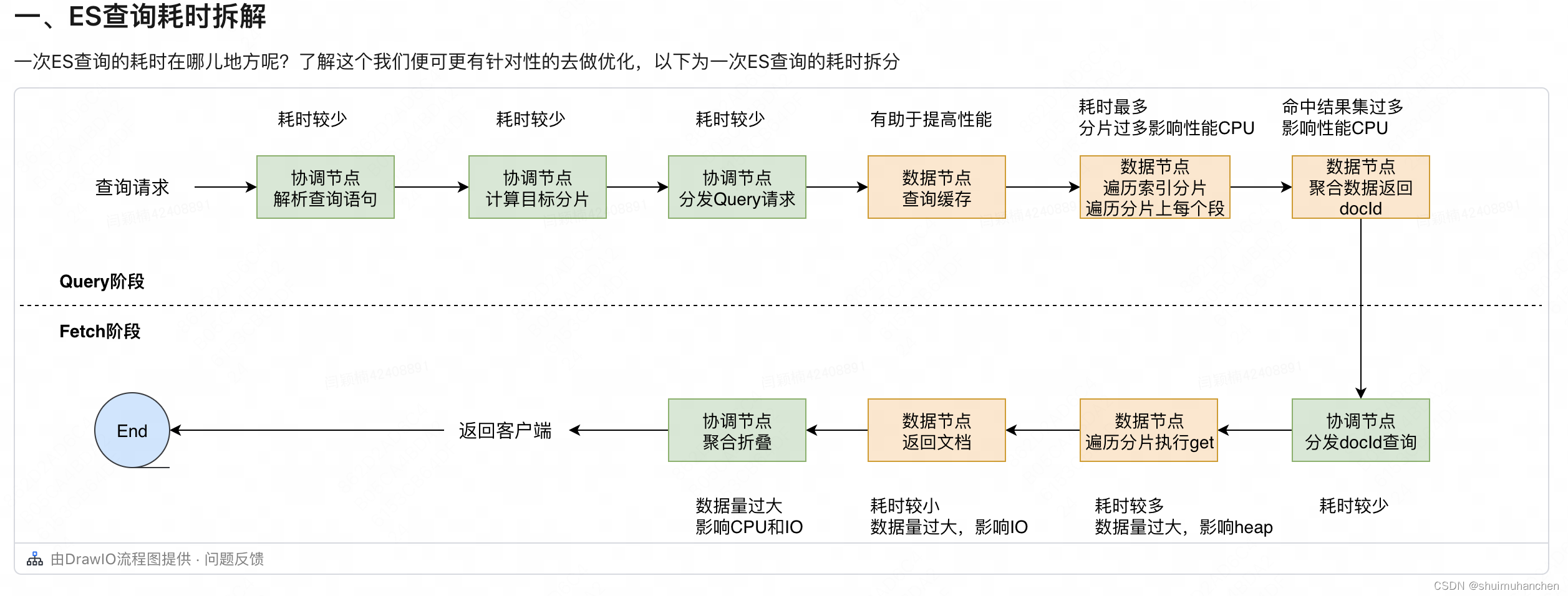
ES实战回顾
1、你用的集群节点情况? 一个ES集群,18个节点,其中3个主节点,15个数据节点,500G左右的索引数据量,没有单独的协调节点,它的每个节点都可以充当协调功能; 2、你们常用的索引有哪些&a…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
