Mamba系列日积月累(一):状态空间模型SSM的离散化过程推导
文章目录
- 1. 背景基础知识
- 1.1 什么是状态空间模型(State Space Model,SSM)?
- 1.2 什么是离散化(Discretization)?
- 1.3 为什么需要离散化?
- 2. SSM离散化过程推导
- 2.1 为什么在离散化过程中要先进行积分?
- 2.2 为什么不直接对 x ˙ ( t ) \dot{x}(t) x˙(t)进行积分?
- 2.2 状态方程的改造以及 α ( t ) \alpha(t) α(t)的设计
- 2.3 离散时间积分近似
- 2.3 状态方程的离散化
- 3. SSM离散化结果
本文首发于: Mamba系列日积月累(一):状态空间模型SSM的离散化过程推导
最近Mamba系列(Mamba、VMamba、Vision Mamba)比较火,在同样具备高效长距离建模能力的情况下,Transformer具有平方级计算复杂度,而Mamba架构则是线性级计算复杂度,并且推理速度更快。
秉承着公众号科研的思路扩展视野的思路,笔者觉得需要学习一下相关内容,于是挑选了目前较新的Vision Mamba论文,准备开始学习。由于缺乏之前的基础知识储备,Preliminaries里面的状态空间模型及其离散化过程直接给我干蒙,想着不能出师未捷身先死,于是决定搜索相关资料,把这个过程弄明白,不过由于本人水平有限,如果内容存在错误,希望大家能给出指导进行纠正。
1. 背景基础知识
1.1 什么是状态空间模型(State Space Model,SSM)?
状态空间模型(State Space Model,简称SSM)是一种数学模型,用于描述和分析动态系统的行为。这种模型在多个领域都有应用,包括控制理论、信号处理、经济学和机器学习等。在深度学习领域,状态空间模型被用来处理序列数据,如时间序列分析、自然语言处理(NLP)和视频理解等。通过将序列数据映射到状态空间,可以更好地捕捉数据中的长期依赖关系。
状态空间模型的核心思想是将系统的当前状态(state) x ( t ) ∈ R n x(t) \in \mathbb{R}^n x(t)∈Rn与输入(input) u ( t ) ∈ R p u(t) \in \mathbb{R}^p u(t)∈Rp和输出(output) y ( t ) ∈ R q y(t) \in \mathbb{R}^q y(t)∈Rq之间的关系用一组方程来表示:
x ˙ ( t ) = A ( t ) x ( t ) + B ( t ) u ( t ) y ( t ) = C ( t ) x ( t ) + D ( t ) u ( t ) (1) \begin{aligned} & \dot{x}(t)=A(t) x(t)+B(t) u(t) \\ & y(t)=C(t) x(t)+D(t) u(t) \end{aligned} \tag{1} x˙(t)=A(t)x(t)+B(t)u(t)y(t)=C(t)x(t)+D(t)u(t)(1)
- 状态方程(State Equation):描述系统状态随时间的演变。状态方程通常包含当前状态和输入,以及可能的系统参数。数学上,状态方程可以表示为: x ˙ ( t ) = A ( t ) x ( t ) + B ( t ) u ( t ) \dot{x}(t)=A(t) x(t)+B(t) u(t) x˙(t)=A(t)x(t)+B(t)u(t), 其中, x ( t ) x(t) x(t)是在时间步 t t t 的系统状态, x ˙ ( t ) \dot{x}(t) x˙(t)是状态向量 x ( t ) x(t) x(t)关于时间 t t t的导数, u ( t ) u(t) u(t) 是在时间步 t t t的输入, A ( t ) A(t) A(t)是状态转移矩阵, dim [ A ( ⋅ ) ] = n × n \operatorname{dim}[A(\cdot)]=n \times n dim[A(⋅)]=n×n, B B B 是输入矩阵, dim [ B ( ⋅ ) ] = n × p \operatorname{dim}[B(\cdot)]=n \times p dim[B(⋅)]=n×p。
- 观测方程(Observation Equation):描述系统输出与状态之间的关系。观测方程允许我们从系统的输出中观察到系统的状态。数学上,观测方程可以表示为: y ( t ) = C ( t ) x ( t ) + D ( t ) u ( t ) y(t)=C(t) x(t)+D(t) u(t) y(t)=C(t)x(t)+D(t)u(t) 其中, y ( t ) y(t) y(t) 是在时间步 t t t 的系统输出, C ( t ) C(t) C(t)是观测矩阵, dim [ C ( ⋅ ) ] = q × n \operatorname{dim}[C(\cdot)]=q \times n dim[C(⋅)]=q×n, D ( t ) D(t) D(t) 是前馈矩阵, dim [ D ( ⋅ ) ] = q × p \operatorname{dim}[D(\cdot)]=q \times p dim[D(⋅)]=q×p。
当式(1)中的所有矩阵均随着时间 t t t而变化时,此时所表示的线性时变系统,而当所有矩阵都不随时间 t t t变化时,此时表示的是线性非时变系统,在Mamba系列中,实际上是线性非时变系统:
x ˙ ( t ) = A x ( t ) + B u ( t ) y ( t ) = C x ( t ) + D u ( t ) (2) \begin{aligned} & \dot{x}(t)=A x(t)+B u(t) \\ & y(t)=C x(t)+D u(t) \end{aligned} \tag{2} x˙(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)(2)
1.2 什么是离散化(Discretization)?
离散化(Discretization)是将连续的数学对象或过程转换为离散形式的过程。在不同的领域中,离散化有着不同的应用和含义,但核心思想是一致的:将连续的变量或函数映射到有限的、离散的集合中。这个过程在数学、工程、计算机科学和许多其他领域中都非常常见。
1.3 为什么需要离散化?
SSM作为一个连续时间系统,其难以直接集成到现代深度学习算法中:
- 计算效率:现代深度学习框架和硬件通常是基于离散时间操作而设计的,对SSM进行离散化后,才能将其转化为可以在这些框架和硬件上高效运行的模型。
- 训练算法:大多数深度学习训练算法,如梯度下降和反向传播,都是为离散时间模型设计的。离散化使得这些算法可以直接应用于状态空间模型,简化了训练过程。
- 实际应用:在许多实际应用中,数据是离散的,如文本数据(单词序列)、时间序列数据(股票价格、传感器读数)等。离散时间模型更自然地与这些数据格式相匹配。
- 模型复杂度:离散化过程可以通过选择合适的时间步长 T T T 来控制模型的复杂度。较小的时间步长可以提供更精细的控制,但计算成本更高;较大的时间步长可以减少计算量,但可能牺牲一些精度。
2. SSM离散化过程推导
这里再贴上状态方程公式
x ˙ ( t ) = A x ( t ) + B u ( t ) (3) \dot{x}(t)=A x(t)+B u(t) \tag{3} x˙(t)=Ax(t)+Bu(t)(3)
为了进行离散化,我们首先要对状态方程(3)进行积分。
2.1 为什么在离散化过程中要先进行积分?
在离散化连续状态方程的过程中,积分是一个关键步骤,因为它涉及到状态变量随时间的累积效应,我们需要考虑在每个离散时间步长内状态变量是如何累积变化的。
在离散时间系统中,我们不能直接处理导数,因为离散时间点上没有导数的概念。相反,我们需要考虑在每个时间步长内状态变量的累积变化。这可以通过对连续时间积分进行离散化来实现,即将连续时间的积分转换为离散时间的求和。
在实际的数值模拟中,我们通常使用数值积分方法(如梯形法则、矩形法则、辛普森法则等)来近似连续时间积分。这些方法允许我们在离散时间点上近似连续时间的累积效应,从而得到离散时间状态方程。这个转换过程涉及到将连续时间的导数项替换为离散时间的差分项,这通常涉及到指数函数和采样间隔 T T T 的计算。
2.2 为什么不直接对 x ˙ ( t ) \dot{x}(t) x˙(t)进行积分?
在式(3)中,假设我们直接对 x ˙ ( t ) \dot{x}(t) x˙(t)进行积分的话,结果如下:
x ( t ) = x ( 0 ) + ∫ 0 t ( A x ( τ ) + B u ( τ ) ) d τ (4) x(t)=x(0)+\int_0^t(A x(\tau)+B u(\tau)) d \tau \tag{4} x(t)=x(0)+∫0t(Ax(τ)+Bu(τ))dτ(4)
此时,积分项中会包含 x ( τ ) x(\tau) x(τ)项本身,由于我们是离散系统,我们是无法获取在一个连续的时刻( 0 → t 0\rightarrow t 0→t)内所有的 x ( τ ) x(\tau) x(τ)值的,因此无法完成该积分结果的计算。
对于离散系统来说,我们希望将公式(4)这个积分表达式转变为以下形式:
x ( k + 1 ) = x ( k ) + ∑ i = 0 k ( A x ( i ) + B u ( i ) ) Δ t (5) x(k+1)=x(k)+\sum_{i=0}^k(A x(i)+B u(i)) \Delta t \tag{5} x(k+1)=x(k)+i=0∑k(Ax(i)+Bu(i))Δt(5)
这个形式要求我们对公式(3)进行一些改造,目标是消除 x ˙ ( t ) \dot{x}(t) x˙(t)表达式中的 x ( t ) x(t) x(t)本身。
2.2 状态方程的改造以及 α ( t ) \alpha(t) α(t)的设计
为了消除 x ˙ ( t ) \dot{x}(t) x˙(t)表达式中的 x ( t ) x(t) x(t)本身,我们通常会构造一个新的函数 α ( t ) x ( t ) \alpha(t)x(t) α(t)x(t),通过对这个新函数进行求导,来简化相应的导数项。
我们对 α ( t ) x ( t ) \alpha(t)x(t) α(t)x(t)进行求导
d d t [ α ( t ) x ( t ) ] = α ( t ) x ˙ ( t ) + x ( t ) d α ( t ) d t (6) \frac{d}{d t}[\alpha(t) x(t)]=\alpha(t) \dot{x}(t)+x(t) \frac{d \alpha(t)}{d t} \tag{6} dtd[α(t)x(t)]=α(t)x˙(t)+x(t)dtdα(t)(6)
我们将公式(3)代入到公式(6)中,替换 x ˙ ( t ) \dot{x}(t) x˙(t):
d d t [ α ( t ) x ( t ) ] = α ( t ) ( A x ( t ) + B u ( t ) ) + x ( t ) d α ( t ) d t (7) \frac{d}{d t}[\alpha(t) x(t)]=\alpha(t) (A x(t)+B u(t))+x(t) \frac{d \alpha(t)}{d t} \tag{7} dtd[α(t)x(t)]=α(t)(Ax(t)+Bu(t))+x(t)dtdα(t)(7)
我们进一步对公式(7)进行改写,合并 x ( t ) x(t) x(t)的相关系数:
d d t [ α ( t ) x ( t ) ] = ( A α ( t ) + d α ( t ) d t ) x ( t ) + B α ( t ) u ( t ) (8) \frac{d}{d t}[\alpha(t) x(t)]=(A\alpha(t) + \frac{d \alpha(t)}{d t})x(t)+B \alpha(t) u(t) \tag{8} dtd[α(t)x(t)]=(Aα(t)+dtdα(t))x(t)+Bα(t)u(t)(8)
由于我们的目的是消除导数项中的 x ( t ) x(t) x(t),因此,我们令 x ( t ) x(t) x(t)的系数项为0即可:
A α ( t ) + d α ( t ) d t = 0 (9) A\alpha(t) + \frac{d \alpha(t)}{d t} = 0 \tag{9} Aα(t)+dtdα(t)=0(9)
此时,我们可以得到 α ( t ) \alpha(t) α(t)的表达式:
α ( t ) = e − A t (10) \alpha(t)=e^{-At} \tag{10} α(t)=e−At(10)
将 α ( t ) \alpha(t) α(t)的表达式代入公式(8)可以得到:
d d t [ e − A t x ( t ) ] = B e − A t u ( t ) (11) \frac{d}{d t}[e^{-At} x(t)]=B e^{-At} u(t) \tag{11} dtd[e−Atx(t)]=Be−Atu(t)(11)
这时我们已经完成了在导数项中消除 x ( t ) x(t) x(t)的目标,对 e − A t x ( t ) e^{-At}x(t) e−Atx(t)进行积分:
e − A t x ( t ) = x ( 0 ) + ∫ 0 t e − A τ B u ( τ ) d τ (12) e^{-At}x(t)=x(0)+\int_0^t e^{-A\tau} B u(\tau) d \tau \tag{12} e−Atx(t)=x(0)+∫0te−AτBu(τ)dτ(12)
对公式(12)进行整理:
x ( t ) = e A t x ( 0 ) + ∫ 0 t e A ( t − τ ) B u ( τ ) d τ (13) x(t)=e^{At}x(0)+\int_0^t e^{A(t-\tau)} B u(\tau) d \tau \tag{13} x(t)=eAtx(0)+∫0teA(t−τ)Bu(τ)dτ(13)
2.3 离散时间积分近似
2.3 状态方程的离散化
在离散系统中,我们需要将公式(13)转化为离散形式,大致步骤如下:
-
参数定义:采样时刻 t k t_k tk和 t k + 1 t_{k+1} tk+1,其中 k k k是采样索引, T T T是采样间隔,即 T = t k + 1 − t k T=t_{k+1}-t_k T=tk+1−tk
-
积分区间离散化:在连续时间积分中,我们通常有一个积分区间,例如从 t t t 到 t + △ t t+\triangle{t} t+△t。在离散时间系统中,我们需要将这个区间划分为 k k k 个等长的子区间,每个子区间的长度为 T T T。
在某个子区间内,公式(13)的形式变为:
x ( t k + 1 ) = e A ( t k + 1 − t k ) x ( t k ) + ∫ t k t k + 1 e A ( t k + 1 − τ ) B u ( τ ) d τ (14) x(t_{k+1})=e^{A(t_{k+1}-t_k)}x(t_{k})+\int_{t_{k}}^{t_{k+1}} e^{A(t_{k+1}-\tau)} B u(\tau) d \tau \tag{14} x(tk+1)=eA(tk+1−tk)x(tk)+∫tktk+1eA(tk+1−τ)Bu(τ)dτ(14) -
近似积分:对于每个子区间来说,考虑使用数值积分方法来近似积分,这里考虑对 u ( t ) u(t) u(t)应用零阶保持法,即假设 u ( t ) u(t) u(t)在采样时刻 t k t_k tk和 t k + 1 t_{k+1} tk+1之间是恒定的,此时,我们可以将 u ( t ) u(t) u(t)当做常数项从积分项中取出:
∫ t k t k + 1 e A ( t − τ ) B u ( τ ) d τ = ∫ t k t k + 1 e A ( t k + 1 − τ ) d τ B u ( t k ) (15) \int_{t_{k}}^{t_{k+1}} e^{A(t-\tau)} B u(\tau) d \tau = \int_{t_{k}}^{t_{k+1}} e^{A(t_{k+1}-\tau)} d \tau B u(t_k) \tag{15} ∫tktk+1eA(t−τ)Bu(τ)dτ=∫tktk+1eA(tk+1−τ)dτBu(tk)(15) -
离散时间状态方程构建:将公式(15)的积分结果代入到公式(14)中,同时使用 T = t k + 1 − t k T=t_{k+1}-t_k T=tk+1−tk进行化简,我们可以得到:
x ( t k + 1 ) = e A T x ( t k ) + ∫ t k t k + 1 e A ( t k + 1 − τ ) d τ B u ( t k ) (16) x(t_{k+1})=e^{AT}x(t_{k})+\int_{t_{k}}^{t_{k+1}} e^{A(t_{k+1}-\tau)} d \tau Bu\left(t_k\right) \tag{16} x(tk+1)=eATx(tk)+∫tktk+1eA(tk+1−τ)dτBu(tk)(16)
引入新变量 λ = t k + 1 − τ \lambda=t_{k+1}-\tau λ=tk+1−τ,对原积分进行简化得到:
x ( t k + 1 ) = e A T x ( t k ) + B u ( t k ) ∫ 0 T e A τ d τ (17) x(t_{k+1})=e^{AT}x(t_{k})+Bu\left(t_k\right)\int_{0}^{T} e^{A\tau} d \tau \tag{17} x(tk+1)=eATx(tk)+Bu(tk)∫0TeAτdτ(17)
这里涉及到矩阵作为指数的积分,这个部分我是查阅一些资料得到的结果:
∫ 0 T e A τ d τ = A − 1 ( e A T − I ) (18) \int_{0}^{T} e^{A\tau} d \tau=A^{-1}(e^{AT}- I) \tag{18} ∫0TeAτdτ=A−1(eAT−I)(18)
最终我们得到了离散时间状态方程:
x ( t k + 1 ) = e A T x ( t k ) + ( e A T − I ) A − 1 B u ( t k ) (19) x(t_{k+1})=e^{AT}x(t_{k})+(e^{AT}- I)A^{-1}B u\left(t_k\right) \tag{19} x(tk+1)=eATx(tk)+(eAT−I)A−1Bu(tk)(19)
3. SSM离散化结果
对比公式(19)和Vision Mamba论文中的离散化结果:

两者形式基本一致,至此,我们完成了SSM的离散化过程的完整推导。
相关文章:

Mamba系列日积月累(一):状态空间模型SSM的离散化过程推导
文章目录 1. 背景基础知识1.1 什么是状态空间模型(State Space Model,SSM)?1.2 什么是离散化(Discretization)?1.3 为什么需要离散化? 2. SSM离散化过程推导2.1 为什么在离散化过程中…...

React中使用LazyBuilder实现页面懒加载方法二
前言: 在一个表格中,需要展示100条数据,当每条数据里面需要承载的内容很多,需要渲染的元素也很多的时候,容易造成页面加载的速度很慢,不能给用户提供很好的体验时,懒加载是优化页面加载速度的方…...

安全测试:史上最全的攻防渗透信息收集方法、工具!
信息收集的意义 信息收集对于渗透测试前期来说是非常重要的。正所谓,知己知彼百战不殆,信息收集是渗透测试成功的保障,只有我们掌握了目标网站或目标主机足够多的信息之后,才能更好地进行渗透测试。 信息收集的方式可以分为两种…...
minio2023版本安装对象存储文件迁移
一、环境 minio版本:minio-20230320201618.0.0.x86_64.rpm 二、安装 将下载好的rpm包放在文件夹下,然后cd到该目录 sudo rpm -ivh minio-20230320201618.0.0.x86_64.rpm 三、启动 1、minio的位置 which minio cd /usr/local/bin 2、启动 (可…...

###C语言程序设计-----C语言学习(7)#(调试篇)
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 一. 程序调试 1.程序调试介绍: 程序调试是软件开发过程中非常重…...
腾讯云Linux(OpenCloudOS)安装tomcat9(9.0.85)
腾讯云Linux(OpenCloudOS)安装tomcat9 下载并上传 tomcat官网 https://tomcat.apache.org/download-90.cgi 下载完成后上传至自己想要放置的目录下 解压文件 输入tar -xzvf apache-tomcat-9.0.85.tar.gz解压文件,建议将解压后的文件重新命名为tomcat,方便后期进…...

动态添加字段和注解,形成class类,集合对象动态创建Excel列
一.需求 动态生成Excel列,因为Excel列是通过类对象字段注解来添加,在不确定Excel列数的情况下,就需要动态生成列,对应类对象字段也需要动态生成; 二.ByteBuddy字节码增强动态创建类 1.依赖 <dependencies><…...
Python爬虫---Scrapy框架---CrawlSpider
CrawlSpider 1. CrawlSpider继承自scrapy.Spider 2. CrawlSpider可以定义规则,再解析html内容的时候,可以根据链接规则提取出指定的链接,然后再向这些链接发送请求,所以,如果有需要跟进链接的需求,意思就是…...

关机恶搞小程序
1. system("shutdown")的介绍 当system函数的参数是"shutdown"时,它将会执行系统的关机命令。 具体来说,system("shutdown")的功能是向操作系统发送一个关机信号,请求关闭计算机。这将触发操作系统执行一系列…...

《HTML 简易速速上手小册》第9章:HTML5 新特性(2024 最新版)
文章目录 9.1 HTML5 新增标签和属性9.1.1 基础知识9.1.2 案例 1:创建一个结构化的博客页面9.1.3 案例 2:使用新的表单元素创建事件注册表单9.1.4 案例 3:创建一个具有高级搜索功能的搜索表单 9.2 HTML5 表单增强9.2.1 基础知识9.2.2 案例 1&a…...

计算机网络之NAT
NAT(网络地址转换,Network Address Translation)是一种网络技术,用于在一个网络与另一个网络之间重新映射IP地址。NAT最常见的应用是在家庭和小型办公室的路由器中,用于将私有(内部)IP地址转换为…...

SQL - 数据操作语句
SQL - 数据操作语句 文章目录 SQL - 数据操作语句数据操作语言-DML1 新增2 修改3 删除4 清空 数据类型1 数值类型2 字符串类型3 日期时间类型 数据操作语言-DML 概念: DML(Data Manipulation Language), 数据操作语言。对数据表数据的增、删…...
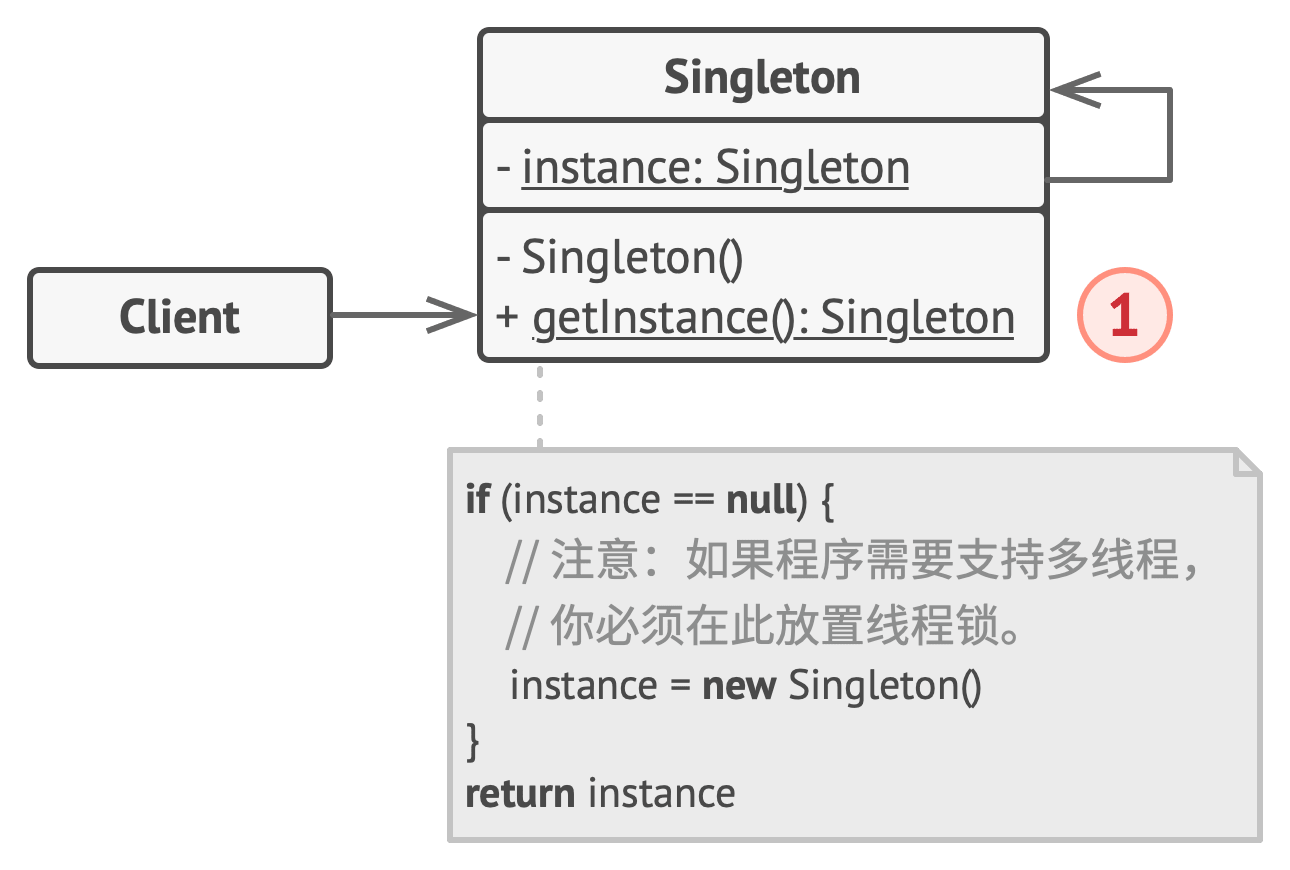
【Python笔记-设计模式】单例模式
一、说明 单例是一种创建型设计模式,能够保证一个类只有一个实例, 并提供一个访问该实例的全局节点。 (一) 解决问题 维护共享资源(数据库或文件)的访问权限,避免多个实例覆盖同一变量,引发程序崩溃。 …...

Java使用io流生成pdf文件
首先生成pdf和正常请求接口一样,直接写~ Controller层: 第一个注解:最顶层增加 Controller 注解(控制器)不多讲了 直接加上。 第二个注解:最顶层增加 CrossOrigin 注解此注解是为了浏览器请求的时候防…...
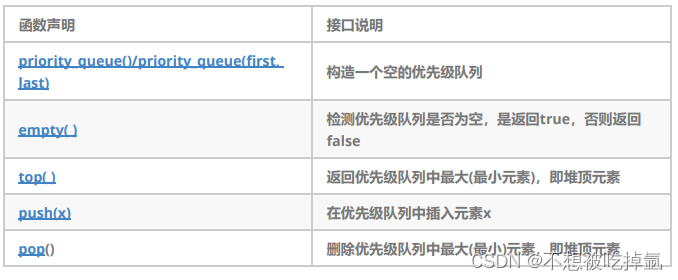
STL-priority_queue
文档 目录 1.关于priority_queued1的定义 2.priority_queue的使用 1.关于priority_queued1的定义 1. 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。 2. 此上下文类似于堆,在堆中可以随时插入元…...

SpringBoot基于注解形式配置多数据源@DS
TOC() 1.引入依赖 <!-- dynamic-datasource 多数据源--><dependency><groupId>com.baomidou</groupId><artifactId>dynamic-datasource-spring-boot-starter</artifactId><version>3.5.2</version></dependency>2.配置…...

华清远见作业第三十四天——C++(第三天)
思维导图: 题目: 设计一个Per类,类中包含私有成员:姓名、年龄、指针成员身高、体重,再设计一个Stu类,类中包含私有成员:成绩、Per类对象p1,设计这两个类的构造函数、析构函数和拷贝构造函数。 代码&#…...

Shell中正则表达式
1.正则表达式介绍 1、正则表达式---通常用于判断语句中,用来检查某一字符串是否满足某一格式 2、正则表达式是由普通字符与元字符组成 3、普通字符包括大小写字母、数字、标点符号及一些其他符号 4、元字符是指在正则表达式中具有特殊意义的专用字符,…...

Flutter Canvas 属性详解与实际运用
在Flutter中,Canvas是一个强大的绘图工具,允许我们以各种方式绘制图形、文字和图像。了解Canvas的属性是开发高度定制化UI的关键。在本篇博客中,我们将深入探讨Flutter中Canvas的一些重要属性,并展示它们在实际应用中的使用。 1.…...

Django配置websocket时的错误解决
基于移动群智感知的网络图谱构建系统需要手机app不断上传数据到服务器并把数据推到前端标记在百度地图上,由于众多手机向同一服务器发送数据,如果使用长轮询,则实时性差、延迟高且服务器的负载过大,而使用websocket则有更好的性能…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
