leetcode—跳跃游戏—贪心算法
1 跳跃游戏1
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
方法:
贪心算法
对于每一个可以到达的位置x,他使得 x+1 , x+2, ... , x+nums[x] 的位置都可以到达
步骤:
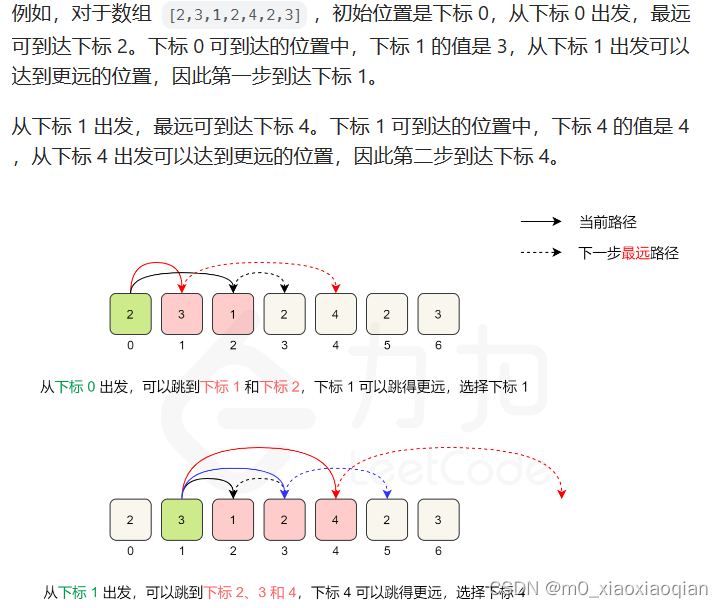
以示例1为例
- 一开始在位置0,可以跳跃2步,因此最远可以到达的位置为0+2=2,将rightmost更新为2,当前到达不了最终位置,继续遍历数组
- 遍历位置1,由于1 < rightmost, 因此1位置可到达,可以跳跃3步,rightmost= 1+3 = 4,4位置刚好到达终点,返回true;
- 若到达不了终点,继续步骤2,直到到达终点或者遍历完数组
- 当遍历完数组,仍然到达不了终点,则返回false
代码
class Solution {public boolean canJump(int[] nums) {int n = nums.length;// 用于记录每次跳跃 可以到达的最远的位置int rightmost = 0;for(int i = 0; i < n; i++){if(i <= rightmost){rightmost = Math.max(rightmost, i + nums[i]);if(rightmost >= n -1){return true;}}}// 若遍历完数组 还是不能到达末尾位置 则返回falsereturn false;}
}2 跳跃游戏2
方法:
在具体的实现中,我们维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加 1。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
代码:
class Solution {public int jump(int[] nums) {int length = nums.length;int end = 0;// 记录当前最大下标位置int maxPosition = 0;// 记录跳跃次数int steps = 0;for(int i = 0; i < length - 1; i++){maxPosition = Math.max(maxPosition, i + nums[i]);// 如果当前位置i等于上一次的结束位置end,说明已经找到了一个可以跳跃到更远位置的方法if(i == end){end = maxPosition;steps++;}}return steps;}
}相关文章:
leetcode—跳跃游戏—贪心算法
1 跳跃游戏1 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1&a…...
Databend 开源周报第 130 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 支持 CREATE OR…...
【web安全】文件上传漏洞
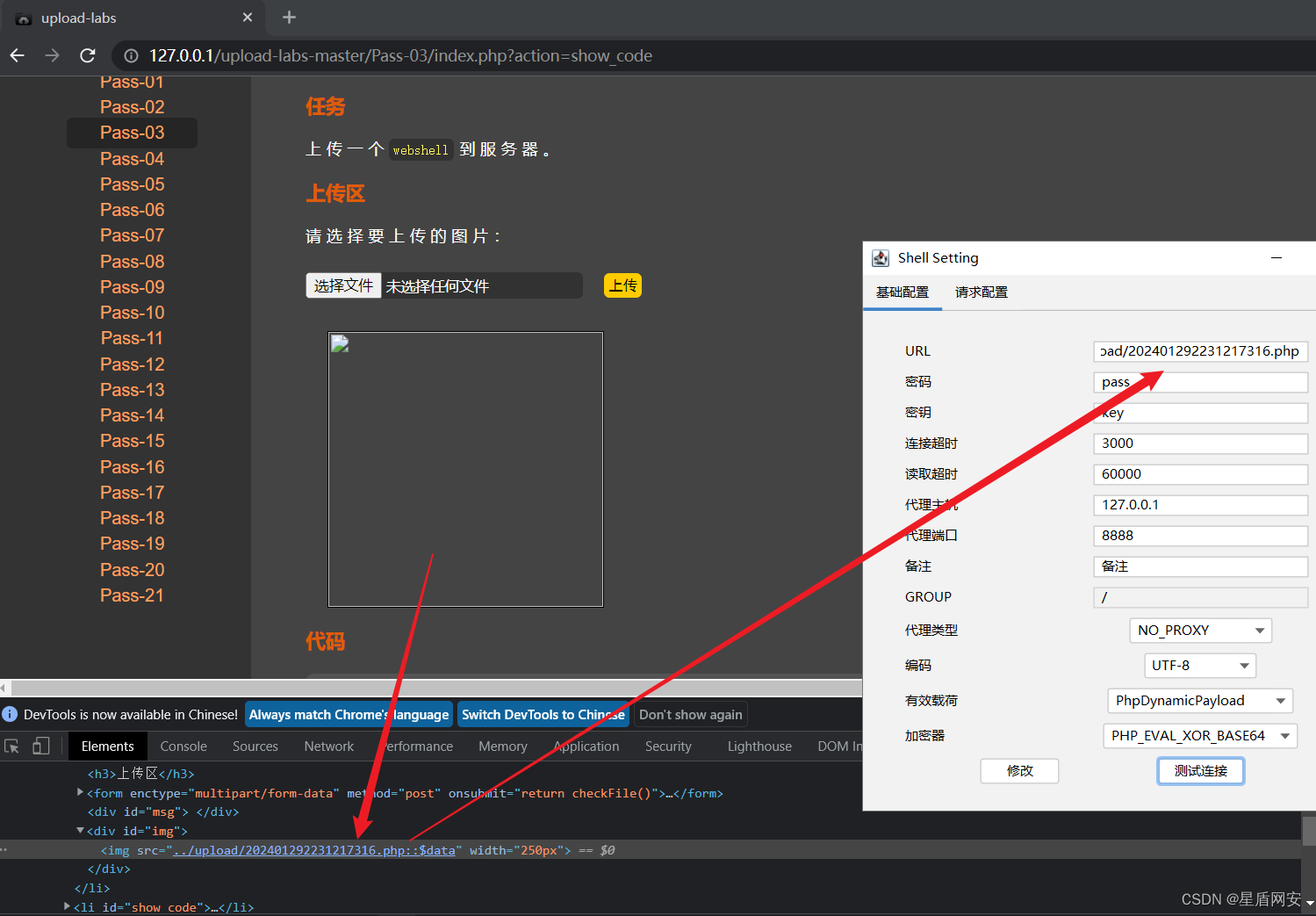
upload-labs靶场 第一关 绕过前端 先打开哥斯拉,生成木马,选择php 打开brup开浏览器,上传文件,就会发现被阻止了,还没抓到包呢 那就是被前端代码阻止了,那通常前端代码都只能防御后缀名 我们抓到包后直…...

C++笔记之RTTI、RAII、MVC、MVVM、SOLID在C++中的表现
C++笔记之RTTI、RAII、MVC、MVVM、SOLID在C++中的表现 —— 杭州 2024-01-28 code review! 文章目录 C++笔记之RTTI、RAII、MVC、MVVM、SOLID在C++中的表现1.RTTI、RAII、MVC、MVVM、SOLID简述2.RAII (Resource Acquisition Is Initialization)3.RTTI (Run-Time Type Informat…...

出口额行业第二再创新高!苏州金龙的2023全球畅行之路
俄罗斯812台、沙特阿拉伯786台、埃塞俄比亚200台、阿尔及利亚445台、韩国382台,苏州金龙2023年海外市场大单频现,全年出口客车5248辆,以超42亿元的出口额创历史新高,稳居行业第二位! 重燃优势主力市场加速度ÿ…...

Python入门到精通(六)——Python函数进阶
Python函数进阶 一、函数的多返回值 二、函数多种传参方式 1、位置参数 2、关键字参数 3、缺省参数 4、不定长参数 (1)位置传递 (2)关键字传递 三、匿名函数 (1)函数作为参数传递 (2&…...

docker: missing signature key
问题描述 下载某些docker镜像时,可能会报missing signature key错误。 原因分析 docker推出了新的镜像构建工具,比较老版本的docker不能识别这种格式。用阿里云镜像源安装的docker版本是1.13.1,这个版本是2017年发布的,需要升级…...

选型 之 工业相机篇
一、概述 23年24年行情不会好,公司各种想办法裁员,在大陆这个大熔炉中只能不断地提炼。我个人主要是在工业领域做2D图像算法和3D算法,但是现在出去都需要全能人才 方案、算法、运动控制等,我目前最大的短板就是方案,在…...

深入解析美颜SDK和动态贴纸技术的工作原理与应用
美颜SDK和动态贴纸技术作为图像处理领域的瑰宝,为用户提供了实时、高质量的美化效果。 一、美颜SDK的工作原理 美颜SDK是一种集成在移动应用、直播平台中的处理工具,通过算法实现实时美颜效果。 1.人脸检测与关键点定位 美颜的第一步是识别图像中的人…...
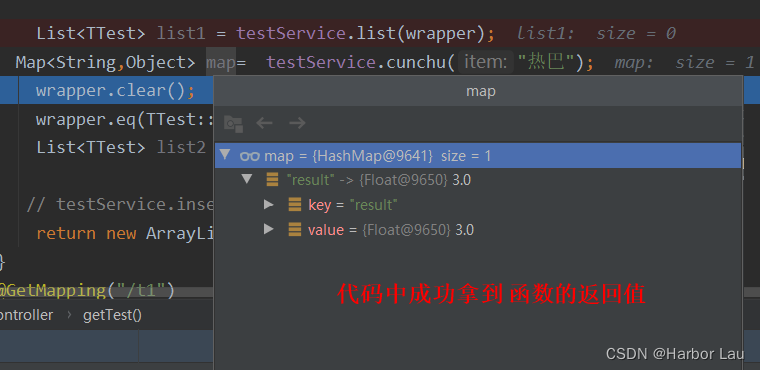
java代码中调用自定义函数
定义函数 CREATE DEFINERrootlocalhost FUNCTION test_fun1(num1 FLOAT,num2 FLOAT) RETURNS float BEGINDECLARE SUM FLOAT DEFAULT 0;SET SUMnum1num2;RETURN SUM; END <select id"cunchu" resultType"java.util.Map">SELECT test_fun1(1,2) as r…...

备战蓝桥杯---数据结构与STL应用(基础实战篇1)
话不多说,直接上题: 当然我们可以用队列,但是其插入复杂度为N,总的复杂度为n^2,肯定会超时,于是我们可以用链表来写,同时把其存在数组中,这样节点的访问复杂度也为o(1).下面是AC代码: 下面我们来…...

项目解决方案:非执法视频监控系统项目设计方案
目 录 一、概述 (一)前言 (二)设计思路 (三)设计原则 1、实用性 2、可靠性 3、安全性 4、先进性 5、开放性 6、易管理、易维护 (四)设计依据 二、方案总…...
网络安全01--负载均衡
目录 一、环境准备 1.1三台虚拟机 二、开始搭建负载均衡: 2.1准备一下源 2.2正式安装 2.3Nginx安装情况 三、负载均衡--轮询(round robin) 3.1在 http 部分添加如下负载均衡配置: 3.2简单解释一下server端: …...

Mamba系列日积月累(一):状态空间模型SSM的离散化过程推导
文章目录 1. 背景基础知识1.1 什么是状态空间模型(State Space Model,SSM)?1.2 什么是离散化(Discretization)?1.3 为什么需要离散化? 2. SSM离散化过程推导2.1 为什么在离散化过程中…...

React中使用LazyBuilder实现页面懒加载方法二
前言: 在一个表格中,需要展示100条数据,当每条数据里面需要承载的内容很多,需要渲染的元素也很多的时候,容易造成页面加载的速度很慢,不能给用户提供很好的体验时,懒加载是优化页面加载速度的方…...

安全测试:史上最全的攻防渗透信息收集方法、工具!
信息收集的意义 信息收集对于渗透测试前期来说是非常重要的。正所谓,知己知彼百战不殆,信息收集是渗透测试成功的保障,只有我们掌握了目标网站或目标主机足够多的信息之后,才能更好地进行渗透测试。 信息收集的方式可以分为两种…...
minio2023版本安装对象存储文件迁移
一、环境 minio版本:minio-20230320201618.0.0.x86_64.rpm 二、安装 将下载好的rpm包放在文件夹下,然后cd到该目录 sudo rpm -ivh minio-20230320201618.0.0.x86_64.rpm 三、启动 1、minio的位置 which minio cd /usr/local/bin 2、启动 (可…...

###C语言程序设计-----C语言学习(7)#(调试篇)
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 一. 程序调试 1.程序调试介绍: 程序调试是软件开发过程中非常重…...
腾讯云Linux(OpenCloudOS)安装tomcat9(9.0.85)
腾讯云Linux(OpenCloudOS)安装tomcat9 下载并上传 tomcat官网 https://tomcat.apache.org/download-90.cgi 下载完成后上传至自己想要放置的目录下 解压文件 输入tar -xzvf apache-tomcat-9.0.85.tar.gz解压文件,建议将解压后的文件重新命名为tomcat,方便后期进…...

动态添加字段和注解,形成class类,集合对象动态创建Excel列
一.需求 动态生成Excel列,因为Excel列是通过类对象字段注解来添加,在不确定Excel列数的情况下,就需要动态生成列,对应类对象字段也需要动态生成; 二.ByteBuddy字节码增强动态创建类 1.依赖 <dependencies><…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
