[数据结构+算法] 给一棵树和一个sum,判断是否存在从root到叶子结点的path之和等于sum?
[数据结构+算法] 给一棵树和一个sum,判断是否存在从root到叶子结点的path之和等于sum?
可以使用两种方法求解
问题转换为递归判断左右子树是否满足路径和等于sum减去当前节点的值。
使用两个栈数据结构,一个存储节点,另一个存储对应的节点到root节点到sum,迭代遍历到叶子节点时进行判断。
详细代码如下:
#include <iostream>
#include <stack>using namespace std;struct TreeNode {TreeNode(int val_) : val(val_), left(nullptr), right(nullptr) {}int val;TreeNode *left;TreeNode *right;
};bool CheckTreeSumRecursive(TreeNode *head, int targetSum) {if (head == nullptr) {return false;}if (head->left == nullptr && head->right == nullptr && head->val == targetSum) {return true;}return CheckTreeSumRecursive(head->left, targetSum - head->val) || CheckTreeSumRecursive(head->right, targetSum - head->val);
}bool CheckTreeSumNonRecursive(TreeNode *head, int targetSum) {if (head == nullptr) {return false;}stack<TreeNode*> nodes;nodes.push(head);stack<int> sums;sums.push(head->val);while (!nodes.empty()) {TreeNode *node = nodes.top();nodes.pop();int sum = sums.top();sums.pop();if (node->left == nullptr && node->right == nullptr && sum == targetSum) {return true;}if (node->left != nullptr) {nodes.push(node->left);sums.push(sum + node->val);}if (node->right != nullptr) {nodes.push(node->right);sums.push(sum + node->val);}}return false;
}// 打印结果的辅助函数
void printResult(bool result) {cout << (result ? "true" : "false") << endl;
}int main() {// 创建示例二叉树TreeNode* root = new TreeNode(5);root->left = new TreeNode(4);root->right = new TreeNode(8);root->left->left = new TreeNode(11);root->left->left->left = new TreeNode(7);root->left->left->right = new TreeNode(2);root->right->left = new TreeNode(13);root->right->right = new TreeNode(4);root->right->right->right = new TreeNode(1);cout << "Test Recursive Solution...\n";cout << "Example 1: ";printResult(CheckTreeSumRecursive(root, 22)); // 输出 truecout << "Example 2: ";printResult(CheckTreeSumRecursive(root, 5)); // 输出 falsecout << "Example 3: ";printResult(CheckTreeSumRecursive(nullptr, 0)); // 输出 falsecout << "Test Recursive Solution...\n";cout << "Example 1: ";printResult(CheckTreeSumNonRecursive(root, 22)); // 输出 truecout << "Example 2: ";printResult(CheckTreeSumNonRecursive(root, 5)); // 输出 falsecout << "Example 3: ";printResult(CheckTreeSumNonRecursive(nullptr, 0)); // 输出 falsereturn 0;
}
相关文章:

[数据结构+算法] 给一棵树和一个sum,判断是否存在从root到叶子结点的path之和等于sum?
[数据结构算法] 给一棵树和一个sum,判断是否存在从root到叶子结点的path之和等于sum? 可以使用两种方法求解 递归 CheckTreeSumRecursive 问题转换为递归判断左右子树是否满足路径和等于sum减去当前节点的值。 迭代 CheckTreeSumNonRecursive 使用两个…...
非阿里云注册域名如何在云解析DNS设置解析?
概述 非阿里云注册域名使用云解析DNS,按照如下步骤: 添加域名。 添加解析记录。 修改DNS服务器。 DNS服务器变更全球同步,等待48小时。 添加解析记录 登录云解析DNS产品控制台。 在 域名解析 页面中,单击 添加域名 。 在 …...
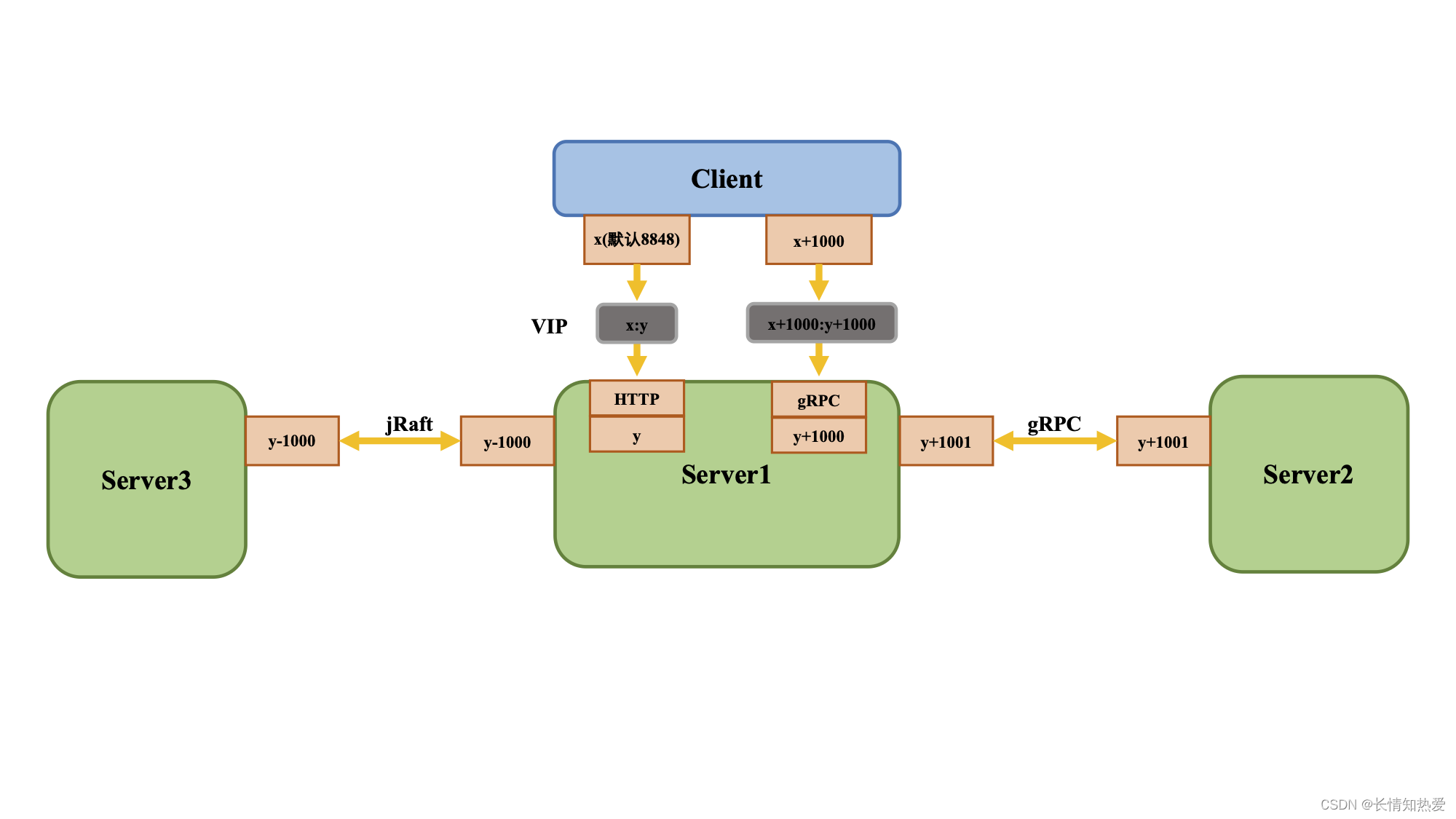
微服务-微服务Alibaba-Nacos注册中心实现
1. 系统架构的演变 俗话说, 没有最好的架构,只有最合适的架构。 微服务架构也是随着信息产业的发展而出现的最有普 遍适用性的一套架构模式。通常来说,我们认为架构发展历史经历了这样一个过程:单体架构——> 垂直架构 ——&g…...

多符号表达式的共同子表达式提取教程
生成的符号表达式,可能会存在过于冗长的问题,且多个符号表达式中,有可能存在相同的计算部分,如果不进行处理,计算过程中会导致某些算式计算多次,从而影响计算效率。 那么多个符号表达式生成函数时…...
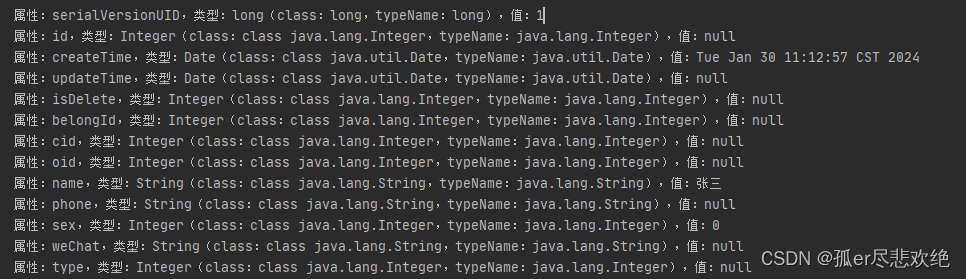
Java 反射获取属性名、属性类型、属性值、判断属性类型
1.代码 /*** 通过反射获取对象属性名、属性类型、属性值** param t 需要反射的对象* author hcx*/public static <T> void reflect(T t){// 获取所有属性// getDeclaredFields 不包含父类,包含私有属性// getFields 包含父类属性Field[] fields t.getClass(…...

Docker私有仓库搭建
目录 1.registry私有仓库 拉取registry镜像 修改docker配置文件并重启 运行registry容器 修改想要上传的镜像的标签并上传验证 再另一台主机上获取此镜像 浏览器验证 2.Docker--harbor私有仓库部署与管理 什么是Harbor Harbor的特性 Harbor的构成 Harbor部署 准备…...
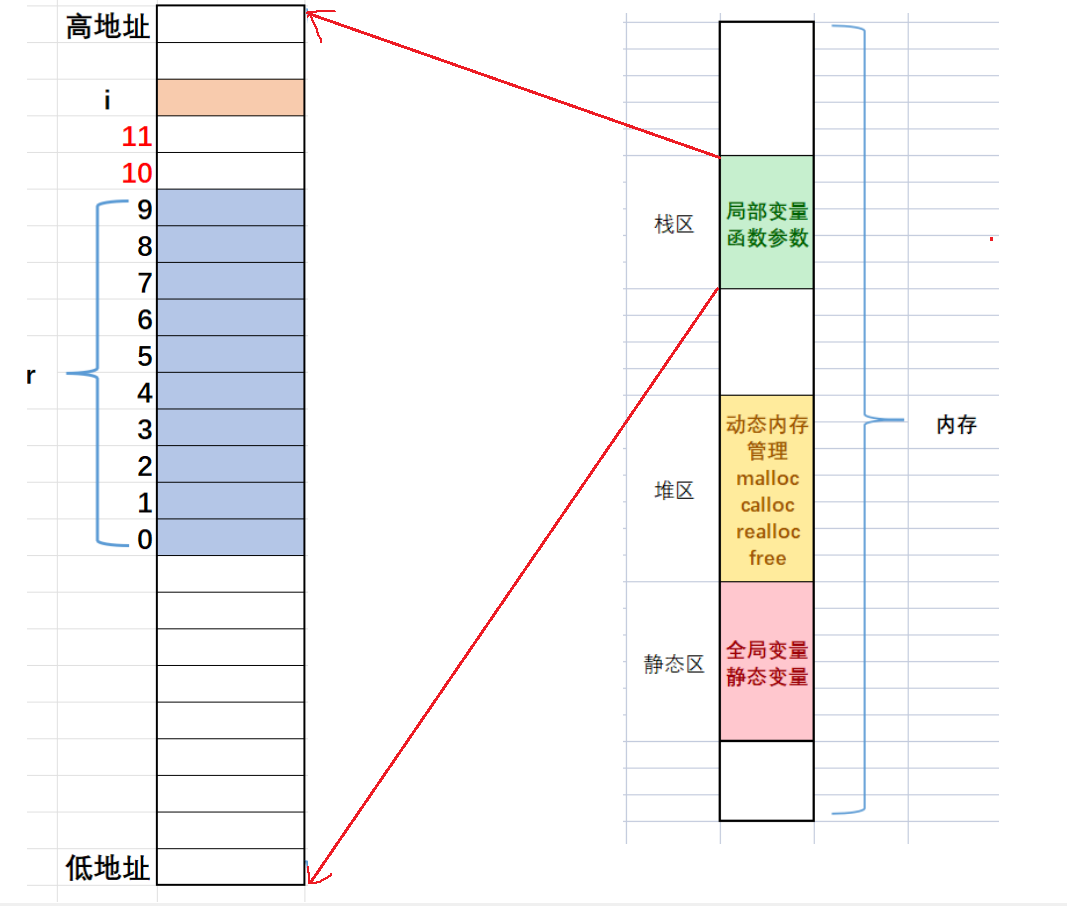
C语言第十三弹---VS使用调试技巧
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 VS调试技巧 1、什么是bug 2、什么是调试(debug)? 3、Debug和Release编辑 4、VS调试快捷键 4.1、环境准备 4.2、调试…...
AST反混淆实战-jsjiamiv7最高配置
js加密混淆网站 https://www.jsjiami.com/一、混淆demo生成 01 打开目标网址 https://www.jsjiami.com/ 02 按照顺序加密混淆二、混淆前后demo 混淆前的源码 (function(w, d) { w.update "2023年01月17日05:34:29更新"; d.info "本站历时1年半研发的新版本V7…...

colorThief+vite+react使用方法
官网: Color Thief npm i --save colorthief 第一种,import载入图片 经过尝试,在vite中,要引入.mjs版本 import ColorThief from colorthief/dist/color-thief.mjs 第一种,通过import载入图片 import aa from /assets/123.jpgconst [resultColor,setResultColor]useState() …...
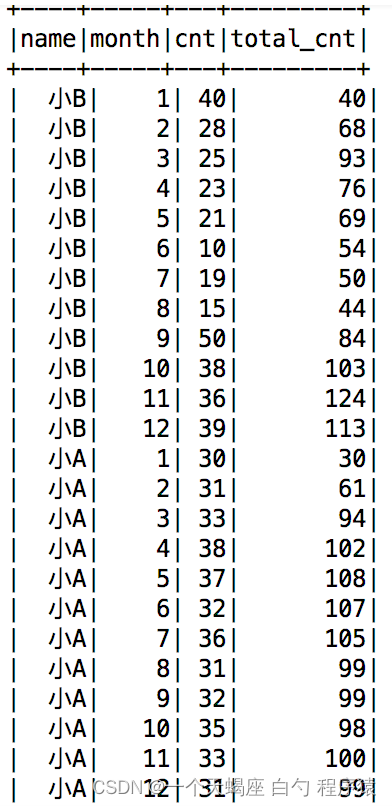
Hive(15)中使用sum() over()实现累积求和和滑动求和
目的: 三个常用的排序函数row_number(),rank()和dense_rank()。这三个函数需要配合开窗函数over()来实现排序功能。但over()的用法远不止于此,本文咱们来介绍如何实现累计求和和滑动求和。 1、数据介绍 三列数据,分别是员工的姓名、月份和…...

2024年Java搭建面试题
2024年Java实战面试题(北京)_java 5 年 面试-CSDN博客 1、搭建docker容器 # 安装依赖的环境 yum -y install yum-utils device-mapper-persistent-data lvm2 # 设置镜像源为阿里 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/lin…...
二维数组的学习
前言 在前面我们学习了一维数组,但是有的问题需要用二位数组来解决。 二维数组常称为矩阵,把二维数组写成行和列的排列形式,可以有助于形象化的理解二维数组的逻辑结构。 一、二维数组的定义 二维数组定义的一般格式: 数据类型 数…...
)
Java集合(List集合)
什么是集合? 什么是集合?集合就是“由若干个确定的元素所构成的整体”,在程序中,一般代表保存 若干个元素(数据)的某种容器类。 在Java中,如果一个Java对象可以在内部持有(保存&…...

7、Json文件的操作总结【robot framework】
1、JSONLibrary简介 Robot Framework 是一种通用的自动化测试框架,它支持使用关键字驱动的测试,并且易于学习和使用。Robot Framework 提供了丰富的标准库,而 JSONLibrary 就是其中之一,用于处理 JSON 数据。 安装 JSONLibrary 在…...

python 循环解压 解压多重压缩包
在实际数据中,经常会有压缩包套压缩包的情况,并且有可能出现“zip”压缩包下面套“tar”的可能。 你可以运行后面的代码,来完成自动解压。代码会不断检查folder_a_path 文件夹下是否还有压缩包。目前支持zip、rar、tar、7z等四种格式的压缩文…...
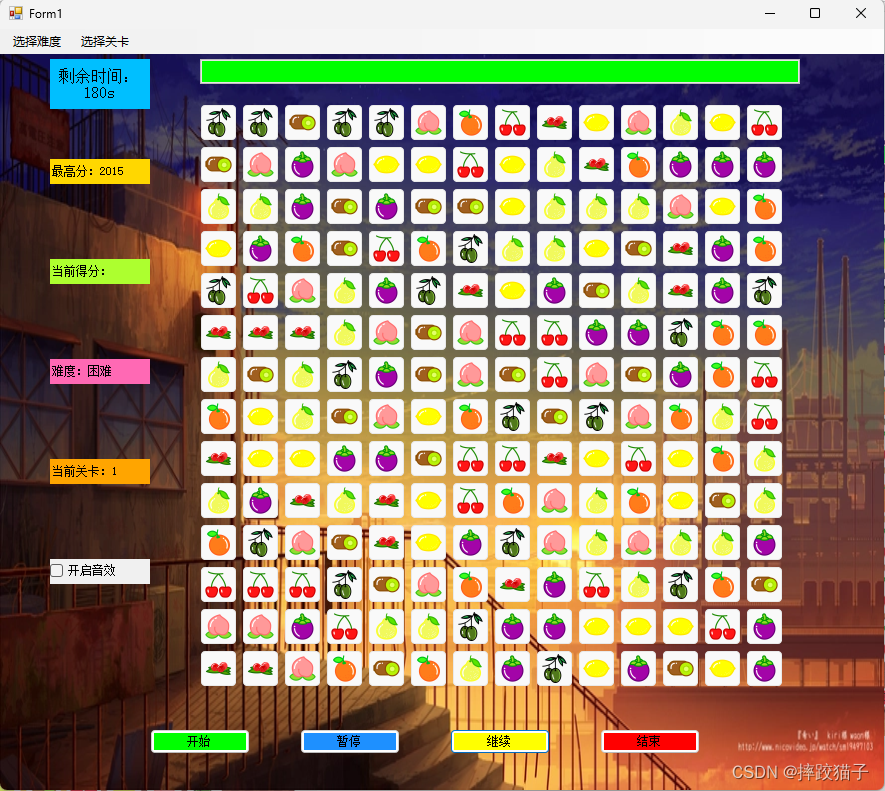
基于C#制作一个连连看小游戏
基于C#制作一个连连看小游戏,实现:难易度选择、关卡选择、倒计时进度条、得分计算、音效播放等功能。 目录 引言游戏规则开发环境准备游戏界面设计游戏逻辑实现图片加载与显示鼠标事件处理游戏优化与扩展添加关卡与难度选择说明</...

Android-System 根据包名查找已安装应用apk方法
1、根据包名查找应用的安装路径 dumpsys package packageName | grep Path 例如: kona:/ # dumpsys package com.yw_pt.oshnoh | grep PathcodePath/data/app/com.yw_pt.oshnoh-N4rPqGh58weRjMpA1q3evwresourcePath/data/app/com.yw_pt.oshnoh-N4rPqGh58weRjMpA1q3…...
洛谷-P4124题-手机号码-Java
题目 题目链接: https://www.luogu.com.cn/problem/P4124 分析 给定两个长度为11位的数字,代表两个区间 [L,R] 需要编写程序来计算出,这两个区间内满足要求的数字个数。这样的题一般来说就是数位dp题。首先我们可以根据容斥原理 [0,R]中满…...
仅使用 Python 创建的 Web 应用程序(前端版本)第08章_商品详细
在本章中,我们将实现一个产品详细信息页面。 完成后的图像如下。 Model、MockDB、Service都是在产品列表页实现的,所以创建步骤如下。 No分类内容1Page定义PageId并创建继承自BasePage的页面类2Application将页面 ID 和页面类对添加到 MultiPageApp 的页面中Page:定义PageI…...

Stable Diffusion 长视频真人动画风格互转
Stable Diffusion Temporal-Kit和EbSynth 从娱乐到商用 1. Temporal Kit 和 EbSynth1.1 提取关键帧1.2 关键帧风格迁移1.3 生成序列帧2. 真人转卡通3. 卡通转真人4. 编辑技巧5. ControlNet + TemporalNet + 达芬奇Fusion6. Rerender A Video7. DiffSynth-Studio基于SD的风格化…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
