代码随想录算法训练营Day38|动态规划理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
目录
动态规划理论基础
什么是动态规划
动态规划的解题步骤
动态规划的debug
509. 斐波那契数
前言
思路
算法实现
方法一:动态规划
方法二:递归法
70. 爬楼梯
前言
思路
算法实现
拓展
746. 使用最小花费爬楼梯
算法实现
总结
动态规划理论基础
什么是动态规划
动态规划,英文名为Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
动态规划的解题步骤
代码随想录中总结了动态规划的五部曲:
- 确定dp数组以及下标的含义;
- 确定递推公式;文章链接
- dp数组如何初始化;
- 确定遍历顺序;
- 举例推导dp数组。
动态规划的debug
写动规题目,代码出问题很正常!找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。如果打印出来和自己预先模拟推导是一样的,那么就是自己的递归公式、初始化或者遍历顺序有问题了。如果和自己预先模拟推导的不一样,那么就是代码实现细节有问题。
这样才是一个完整的思考过程,而不是一旦代码出问题,就毫无头绪的东改改西改改,最后过不了,或者说是稀里糊涂的过了。
509. 斐波那契数
题目链接
文章链接
前言
对于动规,如果没有方法论的话,可能简单题目可以顺手一写就过,难一点就不知道如何下手了。从一开始做题就按照动态规划的五部曲顺序来执行。
思路
按照动态规划五部曲来执行:
- 确定dp数组以及下标的含义:
dp[i]的定义为:第i个数的斐波那契数列值是dp[i];
2.确定递推公式:
题目中已经给出递推公式:dp[i] = dp[i - 1] + dp[i - 2];
3.dp数组初始化:
题目同样已经给出:dp[0] = 0, dp[1] = 1;
4.确定遍历顺序:
前序遍历;
5.举例推导dp数组:
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
算法实现
方法一:动态规划
class Solution {
public:int fib(int n) {if (n <= 1) return n;vector<int> dp(n + 1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};本题的dp实现很简单,因为题目信息已经给出递推公式和初始化值,也可以只维护dp数组前两个值,算法如下:
class Solution {
public:int fib(int n) {if (n <= 1) return n;int dp[2];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {int sum = dp[0] + dp[1];dp[0] = dp[1];dp[1] = sum;}return dp[1];}
};方法二:递归法
还可以使用递归法进行实现,递归的实现较为简单,递归终止条件就是当n小于2。
class Solution {
public:int fib(int n) {if (n < 2) return n;return fib(n - 1) + fib(n - 2);}
};70. 爬楼梯
题目链接
文章链接
前言
本题就没有像上一题一样直接给出递推公式,我们先自=自己举几个例子,就可以发现规律。
思路
按照题目条件爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
利用动态规划五部曲来进行分析:
1.确定dp数组以及下标的含义:
dp[i]的含义是爬到第i层楼梯,有dp[i]种方法;
2.确定递推公式:
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来:一个是dp[i - 1],上i - 1层楼梯,已经有dp[i - 1]种方法,再跳一个台阶就是dp[i];另一个是dp[i - 2],上i - 2层楼梯,已经有dp[i - 2]种方法,那么再跳两个台阶就是dp[i]。因此dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。尤其注意在推导dp[i]的时候,一定要时刻想着dp[i]的定义,否则容易跑偏。这体现出确定dp数组以及下标的含义的重要性!
3.dp数组初始化:
需要注意的是:题目中说了n是一个正整数,题目根本就没说n有为0的情况。所以本题不需要讨论dp[0]的初始化,直接初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推。
4.确定遍历顺序:
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的;
5.举例推导dp数组:
同上题思路一致。
算法实现
class Solution {
public:int climbStairs(int n) {if (n <= 1) return n;vector<int> dp(n + 1);dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};同样也有简化算法,只维护dp数组前面几个元素:
class Solution {
public:int climbStairs(int n) {if (n <= 1) return n;int dp[3];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++){int sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
};拓展
一步一个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种方法爬到n阶楼顶?
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1, 0);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) { if (i - j >= 0) dp[i] += dp[i - j];}}return dp[n];}
};746. 使用最小花费爬楼梯
题目链接
文章链接
算法实现
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size() + 1);dp[0] = 0;dp[1] = 0;for (int i = 2; i <= cost.size(); i++) {dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[cost.size()];}
};简化之后:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int dp[2];dp[0] = 0;dp[1] = 0;for (int i = 2; i <= cost.size(); i++) {int dpi = min(dp[0] + cost[i - 2], dp[1] + cost[i - 1]);dp[0] = dp[1];dp[1] = dpi;}return dp[1];}
};总结
今天了解了动态规划的理论以及较简单题目的实现,在练习过程中熟悉了动态规划五部曲的使用,感觉非常实用!
相关文章:

代码随想录算法训练营Day38|动态规划理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
目录 动态规划理论基础 什么是动态规划 动态规划的解题步骤 动态规划的debug 509. 斐波那契数 前言 思路 算法实现 方法一:动态规划 方法二:递归法 70. 爬楼梯 前言 思路 算法实现 拓展 746. 使用最小花费爬楼梯 算法实现 总结 动态规划…...

C++中的指针空值nullptr
一、nullptr的引入 在C98中,通常是用NULL或者0对指针变量进行初始化 int* p1 NULL; int* p2 0; NULL其实一个宏,本质是0,在传统C头文件stddef.h中给可以看到如下代码 #ifndef NULL #ifdef __cplusplus #define NULL 0 #else #define …...
【Linux网络编程】网络编程套接字(1)
【Linux网络编程】网络编程套接字(1) 目录 【Linux网络编程】网络编程套接字(1)源IP地址和目的IP地址端口号端口号和进程ID的关系 网络通信TCP协议UDP协议网络字节序socket编程接口简单的UDP网络程序 作者:爱写代码的刚子 时间:2024.1.29 前言࿱…...
vite+ts+vue3打包的过程和错误
文章目录 概要vite.config.ts配置tsconfig.json 的配置package.json 的配置路由配置打包打开打包后的文件小结 概要 完成vite的打包,和在本地打开页面 记录一下,vite打包过程中的问题!!! vite.config.ts配置 vite.config.ts配置打包的相关配置 import…...
-面试经典150题)
80.双指针实现删除有序数组中的重复项 II(中等)-面试经典150题
题目 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。 说明…...
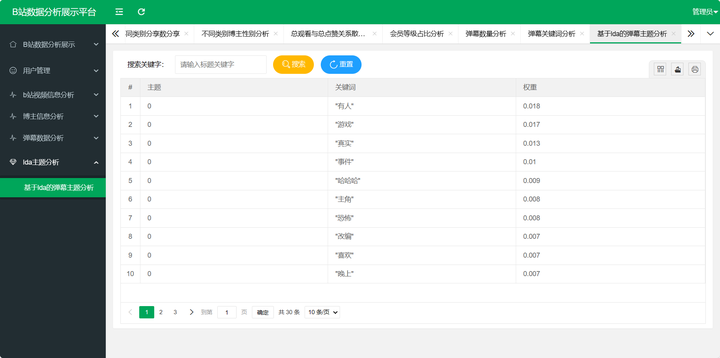
基于大数据的B站数据分析系统的设计与实现
摘要:随着B站(哔哩哔哩网)在国内视频分享平台的崛起,用户规模和数据量不断增加。为了更好地理解和利用这些海量的B站数据,设计并实现了一套基于Python的B站数据分析系统。该系统采用了layui作为前端框架、Flask作为后端…...

机器学习模型预测贷款审批
机器学习模型预测贷款审批 作者:i阿极 作者简介:数据分析领域优质创作者、多项比赛获奖者:博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论&…...
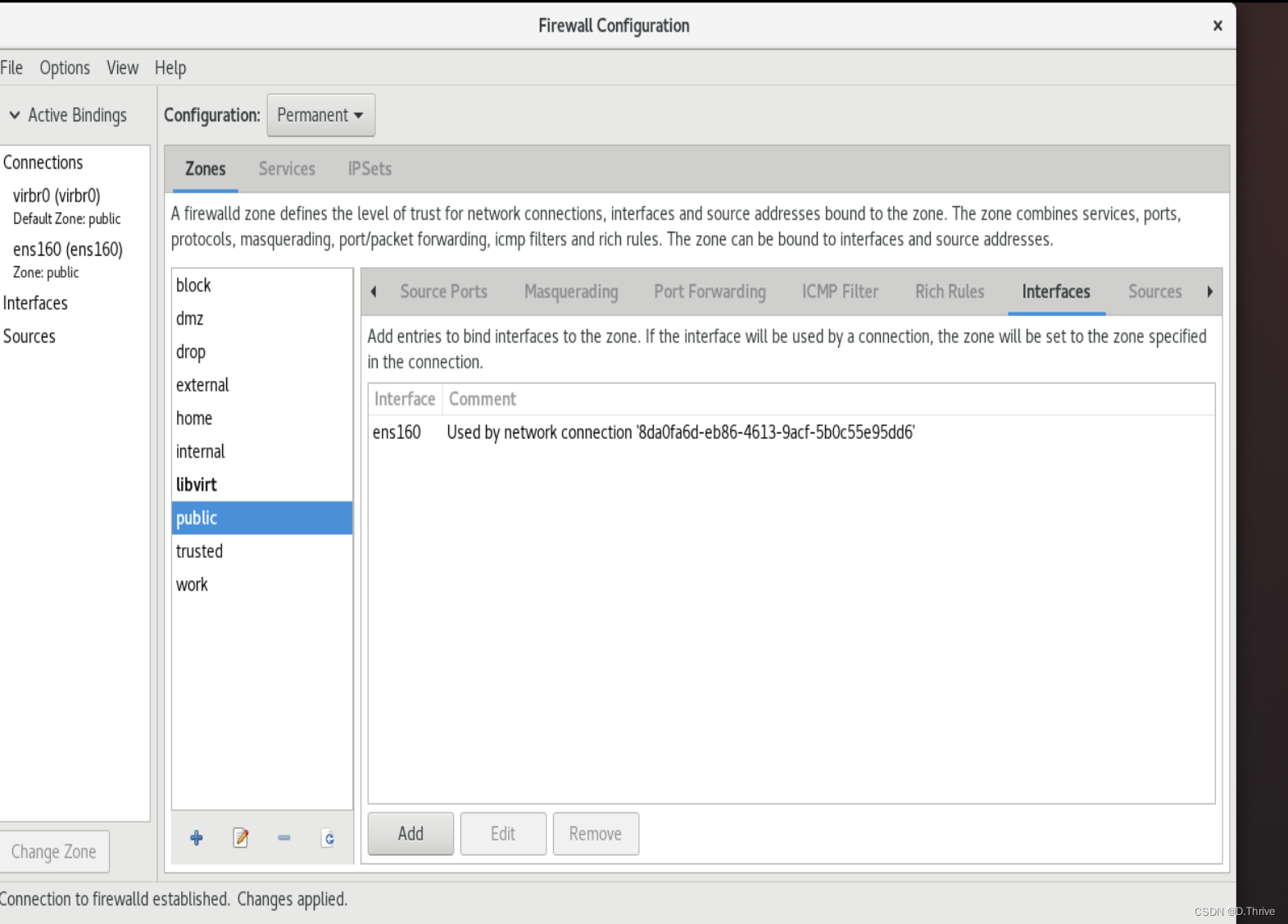
Linux实验记录:使用firewalld
前言: 本文是一篇关于Linux系统初学者的实验记录。 参考书籍:《Linux就该这么学》 实验环境: VmwareWorkStation 17——虚拟机软件 RedHatEnterpriseLinux[RHEL]8——红帽操作系统 备注: RHEL8系统中集成了多款防火墙管理工具…...

Vue之初识Vue CLI 脚手架
Vue CLI 是Vue 官方提供的一个全局命令工具 可以帮助我们快速创建一个开发Vue项目的标准化基础架子。【集成了webpack配置】 脚手架有什么好处? 1.开箱即用,零配置 2.内置 babel 等工具 3.标准化 使用步骤: 1.全局安装(一次):yarn globaladd vue/cli …...
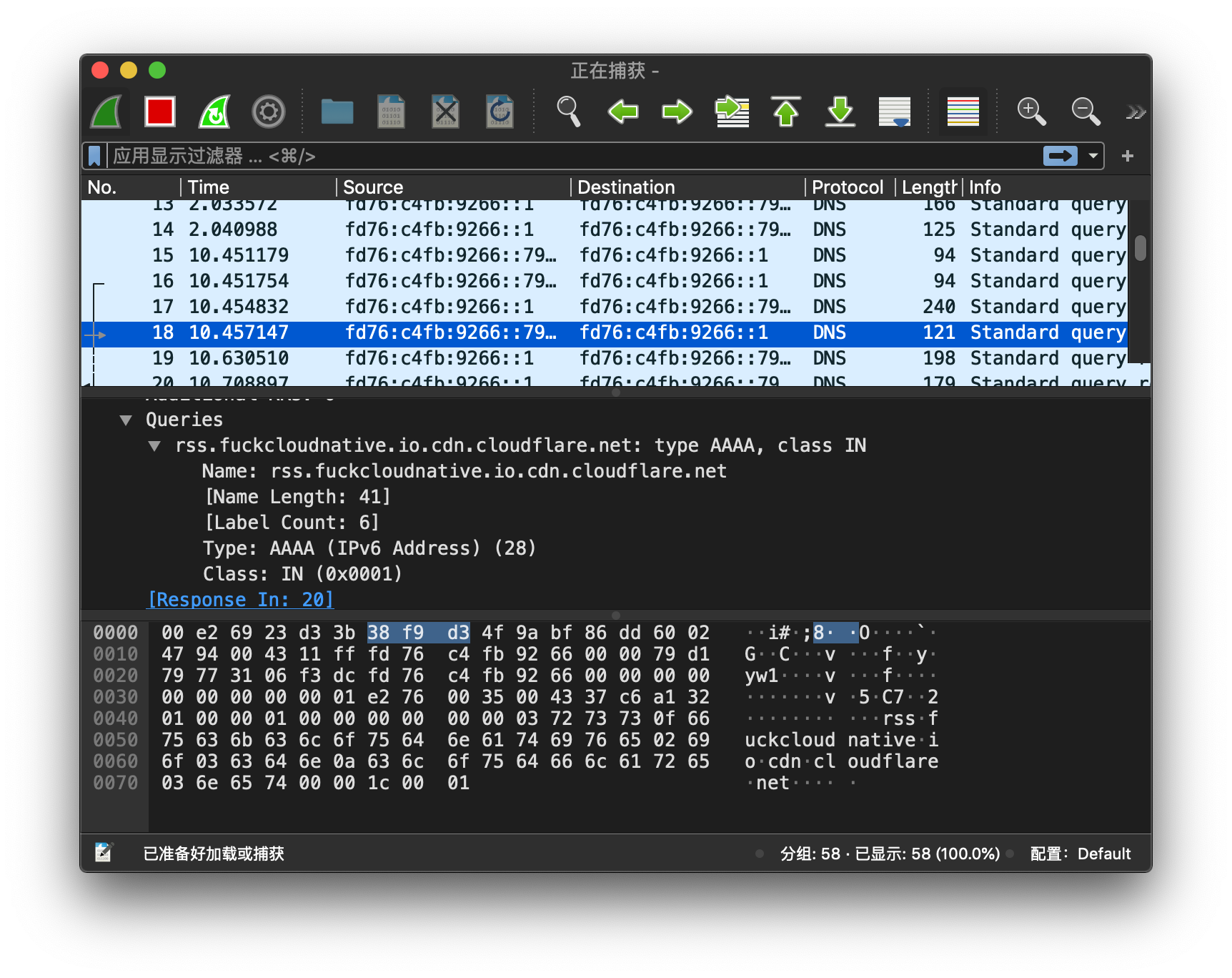
[Tcpdump] 网络抓包工具使用教程
往期回顾 海思 tcpdump 移植开发详解海思 tcpdump 移植开发详解 前言 上一节,我们已经讲解了在海思平台如何基于静态库生成 tcpdump 工具,本节将作为上一节的拓展内容。 一、tcpdump 简介 「 tcpdump 」是一款强大的网络抓包工具,它基于…...

MongoDB常用命令
3.1 案例需求 存放文章评论的数据存放到MongoDB中,数据结构参考如下: 数据库:articledb 3.2 数据库操作 3.2.1 选择和创建数据库 选择和创建数据库的语法格式: use 数据库名称 如果数据库不存在则自动创建,例如&a…...

强敌环伺:金融业信息安全威胁分析——整体态势
从早期的Zeus和其他以银行为目标的特洛伊木马程序,到现在的大规模分布式拒绝服务(DDoS)攻击,再到新颖的钓鱼攻击和勒索软件,金融服务业已成为遭遇网络犯罪威胁最严重的行业之一。金融服务业的重要性不言而喻࿰…...

FreeRTOS简介
一 FreeRTOS简介 实时操作系统(Real-Time Operating System,RTOS)是一种专门设计用于处理实时任务的操作系统。它的主要作用是提供具有严格时间约束的任务调度和资源管理,以满足实时系统对时间的要求。 可分为硬实时和软实时&am…...

51单片机点灯
51单片机点灯 1.点亮LED灯 #include "reg52.h"sbit ledOne P3^7;void main() {//灯亮,给一个P3.7低电平ledOne 0; }给LED1对应标号的P3^7一个低电平,就能点亮LED灯2.LED灯闪烁 #include "reg52.h"sbit ledOne P3^7;void Delay…...

sql注入之union联合注入
一、Union注入 联合查询注入是联合两个表进行注入攻击,使用关键词 union select 对两个表进行联合查询。两个表的字段数要相同,不然会出现报错。列数相同 union 特性是显示两张表 我们就可以吧第一个参数变为------负--的 或者不存在的值 就行了 显示就…...

activiti解决实现ExecutionListener spring 自动注入@Autowired为null问题
在 Activiti 中,当使用 ExecutionListener 时,Spring 的自动注入机制(例如 Autowired)可能无法正常工作。这是因为 ExecutionListener 是由 Activiti 管理的,并不是由 Spring 管理的,所以无法通过 Autowire…...
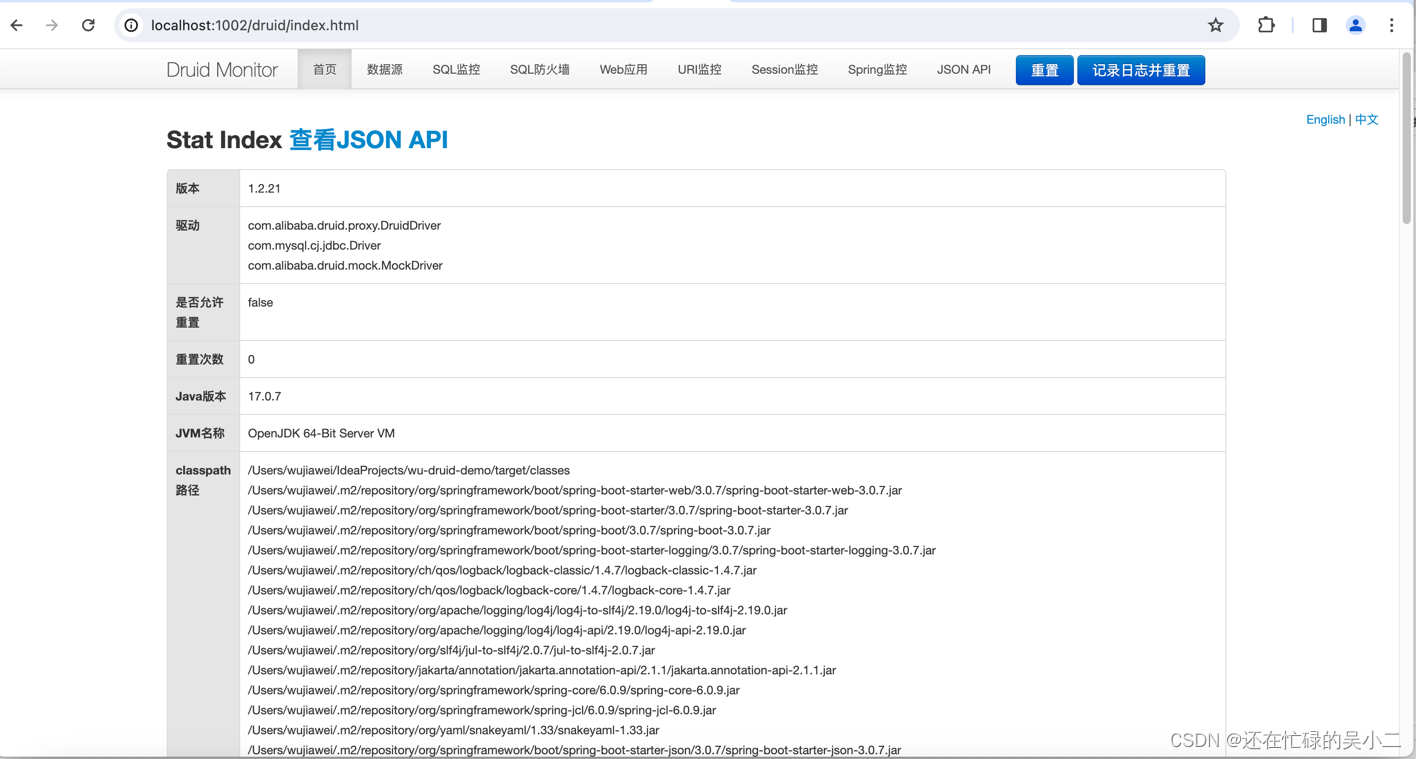
【Lazy ORM 整合druid 实现mysql监控】
Lazy ORM 整合druid 实现mysql监控 JDK 17 Lazy ORM框架地址 up、up欢迎start、issues 当前项目案例地址 框架版本描述spring-boot3.0.7springboot框架wu-framework-web1.2.2-JDK17-SNAPSHOTweb容器Lazy -ORM1.2.2-JDK17-SNAPSHOTORMmysql-connector-j8.0.33mysql驱动druid-…...

【Deeplabv3+】Ubutu18.04中使用pytorch复现Deeplabv3+第三步)-----CityscapesScripts生成自己的标签
本文是在前面两篇文章的基础上,讲解如何更改训练数据集颜色,需要与前面两篇文章连起来看。 本文用于修改cityscapes数据集的标签颜色与Semankitti数据集的标签一致,对修改后的数据集进行训练。需要下载两个开发工具包和一个数据集࿰…...
》笔记3.3)
《动手学深度学习(PyTorch版)》笔记3.3
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。…...

OpenGL ES 渲染 NV21、NV12 格式图像有哪些“姿势”?
使用2个纹理实现 NV21 格式图像渲染 前文提到渲染 NV21 格式图像需要使用 2 个纹理,分别用于保存 Y plane 和 UV plane 的数据,然后在片段着色器中分别对 2 个纹理进行采样,转换成 RGB 数据。 OpenGLES 渲染 NV21或 NV12 格式图像需要用到 GL_LUMINANCE 和 GL_LUMINANCE_A…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

Qt 按钮类控件(Push Button 与 Radio Button)(1)
文章目录 Push Button前提概要API接口给按钮添加图标给按钮添加快捷键 Radio ButtonAPI接口性别选择 Push Button(鼠标点击不放连续移动快捷键) Radio Button Push Button 前提概要 1. 之前文章中所提到的各种跟QWidget有关的各种属性/函数/方法&#…...

FTPS、HTTPS、SMTPS以及WebSockets over TLS的概念及其应用场景
一、什么是FTPS? FTPS,英文全称File Transfer Protocol with support for Transport Layer Security (SSL/TLS),安全文件传输协议,是一种对常用的文件传输协议(FTP)添加传输层安全(TLS)和安全套接层(SSL)加密协议支持的扩展协议。…...

STM32CubeMX-H7-19-ESP8266通信(中)--单片机控制ESP8266实现TCP地址通信
前言 上篇文章我们已经能够使用串口助手实现esp8266的几种通信,接下来我们使用单片机控制实现。这篇文章会附带教程,增加.c和,.h,把串口和定时器放到对应的编号,然后调用初始化就可以使用了。 先讲解,然后末尾再放源码…...

鼠标的拖动效果
1、变量的设置 let isDragging false; let startX; let startY; let endX; let endY; let box null;isDragging : 表示是否推拽startX、startY:表示起始坐标,相对于元素endX、endY:表示结束坐标,相对于元素box&…...

Spring AOP执行原理源码解析
对【com.example.demo.TestAspect#aopTest】连接点增加了五个通知 在调用【com.example.demo.A#testAop()】(用户自定义)方法时,Cglib拦截器对其进行了拦截 可以看到执行顺序分别是环绕前置,前置,环绕后置,…...
