动态规划入门题目
动态规划(记忆化搜索):
将给定问题划分成若干子问题,直到子问题可以被直接解决。然后把子问题的答保存下来以免重复计算,然后根据子问题反推出原问题解的方法
动态规划也称为递推(暴力深搜+记忆中间状态结果)其中:
- 递推公式 = dfs向下递归的公式
- 递推列表的初始值 = 递归的边界
文章目录
- 一、爬楼梯
- 思路
- 解题方法
- 复杂度
- 复杂度
- 二、三角形最小路径和
- 思路
- 思路
- 解题方法
- 复杂度
- 复杂度
- 三、大盗阿福
- 思路
- 解题方法
- 复杂度
一、爬楼梯
Problem One: 70. 爬楼梯
题目描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
输入:
输入一个整数表示台阶数 n
输出:
返回一个整数,表示爬到楼顶的方案数。
思路
- 对第一级台阶,方案数等于1,对第二级台阶,方案数为2(直接迈两级或迈两次一级)
- 对于第i级台阶(i >= 3)来说,它的前驱台阶可能是i-1,也可能是i-2,所以从第0阶台阶上到第i阶台阶的方案数等于上到第i-1阶台阶的方案数加上上到第i-2阶台阶的方案数。
解题方法
创建一个dp[]列表存储到达每一级台阶的方案数,使用for循环从小到大逐步求出所有台阶对应的方案数,最后返回dp[n-1]即可
复杂度
时间复杂度:
O ( n ) O(n) O(n)
空间复杂度:
O ( n ) O(n) O(n)
class Solution:def climbStairs(self, n: int) -> int:if n == 0:return 0elif n == 1:return 1dp = [0]*(n+1)dp[0], dp[1], dp[2] = 0, 1, 2for i in range(3, n+1):dp[i] = dp[i-1] + dp[i-2]return dp[-1]
根据 动态规划 = 记忆化搜索 的理念可知,本题可以直接使用暴力搜索完成,但算法的复杂度有明显差异。
复杂度
时间复杂度:
O ( 2 n ) O(2^n) O(2n)
空间复杂度:
O ( 1 ) O(1) O(1)
# 使用DFS直接搜索
# 时间复杂度:O(2的n次方)
def f(n)->int:if n <= 0:return 0elif n == 1:return 1elif n == 2:return 2else :return f(n-1)+f(n-2)print(f(int(input())))
二、三角形最小路径和
Problem Two: LCR 100. 三角形最小路径和
题目描述:
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
输入:
输入一个二维列表表示三角形
例如:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:
返回一个整数,表示最小路径和。
思路
- 对第一级台阶,方案数等于1,对第二级台阶,方案数为2(直接迈两级或迈两次一级)
- 对于第i级台阶(i >= 3)来说,它的前驱台阶可能是i-1,也可能是i-2,所以从第0阶台阶上到第i阶台阶的方案数等于上到第i-1阶台阶的方案数加上上到第i-2阶台阶的方案数。
思路
题目是一个标准的深度优先搜索问题,因为每一层中的元素会多次被使用,所以可以通过创建列表存储到达该点所需要的最小路径和(记忆化搜索)的方式提升效率。记忆化搜索也就是动态规划。
解题方法
自然的方法是自上而下,找出每一层各元素到三角形上顶点的最小路径和,然后在最后一层中选出最小路径。但这种方法中每一层的元素需要分成左端点、中间节点和右端点三类,最后还需要遍历一整行找出最小值,算法的时间复杂度较高。
- 最左侧的节点:前驱节点只能是tri[i-1][0]
- 最右侧的节点:前驱节点只能是tri[i-1][i-1]
- 中间的节点 :前驱节点可以是tri[i-1][j] or tri[i-1][j+1]
复杂度
时间复杂度:
O ( n 2 ) O(n^2) O(n2)
空间复杂度:
O ( n ) O(n) O(n)
# 自上而下计算最小和
def f()->int:# 读取输入n = int(input())tri = []for i in range(n):tri.append([int(j) for j in input().split()])# 算法主体if not tri:# 如果列表为空,返回0return 0rows = len(tri)dp = []# 第一行特殊处理dp.append([tri[0][0]])for i in range(1, rows):temp = []for j in range(i+1):if j == 0:temp.append(tri[i][0]+dp[i-1][0])elif j < i:temp.append(tri[i][j]+min(dp[i-1][j-1], dp[i-1][j]))else:temp.append(tri[i][j]+dp[i-1][j-1])dp.append(temp)return min(dp[-1])
print(f())
算法优化:
通过对题目的观察可知题目不要求找出最短路径中的每一个元素,所以也可以自下而上的查找,存储每一个元素到最后一层的最小路径和。这样每一层只有一种节点(前驱节点一定是 tri[i+1][j] 和 tri[i+1][j+1] 二选一),不必区分左右端点,而且最后只需返回dp[0][0]即可,因为dp[0][0]存储的就是三角形上顶点到三角形最下层的最小路径和。
复杂度
时间复杂度:
O ( n 2 ) O(n^2) O(n2)
空间复杂度:
O ( n ) O(n) O(n)
# 除了自上而下的计算,还可以自下而上地求出dp列表的值
# 在自下而上的过程中,三角形每一层都只有一种节点,更为简单
def f()->int:n = int(input())tri = []for i in range(n):tri.append([int(j) for j in input().split()])# 算法主体# 创建dp列表dp = tri[:]for row in range(n-2, -1, -1):for col in range(row+1):dp[row][col] = min(dp[row+1][col], dp[row+1][col+1]) + tri[row][col]return dp[0][0]print(f())
三、大盗阿福
Problem Three: 信息学奥赛一本通 1301. 大盗阿福
题目描述:
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N 家店铺,每家店中都有一些现金。阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入:
输入的第一行是一个整数T(T≤50) ,表示一共有T组数据。
接下来的每组数据,第一行是一个整数N(1≤N≤100,000) ,表示一共有N家店铺。第二行是N个被空格分开的正整数,表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过1000。
输出:
对于每组数据,输出一行。该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
思路
分析可知,被选中的两家店之间可能间隔1家店,也可能间隔2家店,但不可能间隔大于等于3家店,因为间隔的三家店中中间的那一家也可以同时被选中,如果不选,则该方案一定不是最优方案。所以本题实质上与爬楼梯相似,都是典型的动态规划题目。
解题方法
创建一个列表dp记录从左向右打劫到每一个店铺时所能获得的最大金额,最后dp中的最大值即为所求。
- 第一家店铺:最大金额等于该店铺的钱数
- 第二家店铺:最大金额等于 max(money[0], money[1])
- 第三家店铺:最大金额等于 max(money[1], money[0]+money[2])
- 第i(i > 3)家店铺:最大金额等于 money[i-1] + max(dp[i-2], dp[i-3])
复杂度
时间复杂度:
O ( n ) O(n) O(n)
空间复杂度:
O ( n ) O(n) O(n)
def f(n, money):# n = len(money)if n == 1:print(money[0])return elif n == 2:print(max(money))returnelif n == 3:print(max(money[1], money[0]+money[2]))return# 初始化dp列表dp = [0]*ndp[0] = money[0]dp[1] = max(money[0], money[1])dp[2] = max(money[1], money[0] + money[2])for i in range(3, n):dp[i] = money[i] + max(dp[i-2], dp[i-3])print(max(dp))t = int(input())
for i in range(t):f(int(input()), [int(k) for k in input().split()])
相关文章:

动态规划入门题目
动态规划(记忆化搜索): 将给定问题划分成若干子问题,直到子问题可以被直接解决。然后把子问题的答保存下来以免重复计算,然后根据子问题反推出原问题解的方法 动态规划也称为递推(暴力深搜记忆中间状态结果…...

探索云性能测试的各项功能有哪些?
云性能测试作为现代软件开发和部署过程中不可或缺的一环,为确保系统在各种条件下的高效运行提供了关键支持。本文将介绍云性能测试的各项功能,帮助您更好地了解其在软件开发生命周期中的重要性。 1. 负载测试 云性能测试的首要功能之一是负载测试。通过模…...
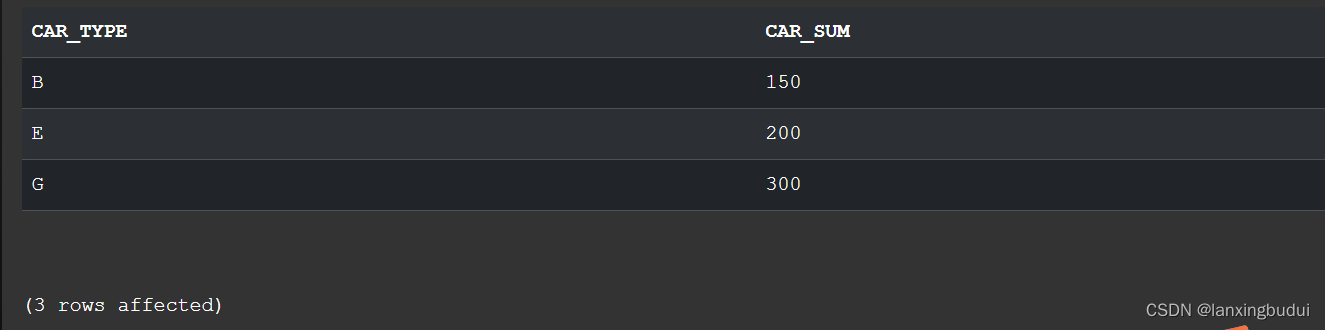
(大众金融)SQL server面试题(1)-总销售量最少的3个型号的车及其总销售量
今天,面试了一家公司,什么也不说先来三道面试题做做,第一题。 那么,我们就开始做题吧,谁叫我们是打工人呢。 题目是这样的: 统计除豪车外,销售最差的车 车辆按批销售,每次销售若干…...
Git安装,Git镜像,Git已安装但无法使用解决经验
git下载地址: Git - 下载 (git-scm.com) <-git官方资源 Git for Windows (github.com) <-github资源 CNPM Binaries Mirror (npmmirror.com) <-阿里镜像(推荐,镜…...
分类提取坐标到excel(补充圆半径、线长度、圆弧))
Python与CAD系列高级篇(二十五)分类提取坐标到excel(补充圆半径、线长度、圆弧)
目录 0 简述1 分类提取坐标到excel2 结果展示0 简述 上一篇中介绍了:对点、直线、多段线、圆、样条曲线分类读取坐标并提取到excel。考虑到进一步提取图形信息,此篇补充对圆半径、线长度以及圆弧几何信息的提取。 1 分类提取坐标到excel 代码实现: import math import nump…...

Linux安装Influxdb
Linux安装Influxdb 1、安装步骤1.1、安装Influxdb步骤1.2、Influxdb默认安装路径1.3、命令行操作Influxdb,建库,建用户1.3.1 进入influxdb命令行1.3.2 创建用户1.3.2 库查询和创建 1、安装步骤 1.1、安装Influxdb步骤 yum install -y wget #下载安装包…...

Flutter CustomPainter 属性介绍与使用
Flutter 中的 CustomPainter 是一个强大的工具,允许开发者通过自定义绘制来创建各种复杂的图形和动画。本文将介绍 CustomPainter 的一些重要属性以及如何使用它们来实现自定义绘制。 1. CustomPainter 简介 CustomPainter 是一个抽象类,用于自定义绘制…...
基于Javaweb开发的二手图书零售系统详细设计【附源码】
基于Javaweb开发的二手图书零售系统详细设计【附源码】 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承接各种定制系统…...
【JaveWeb教程】(35)SpringBootWeb案例之《智能学习辅助系统》登录功能的详细实现步骤与代码示例(8)
目录 案例-登录和认证1. 登录功能1.1 需求1.2 接口文档1.3 思路分析1.4 功能开发1.5 测试 案例-登录和认证 在前面的课程中,我们已经实现了部门管理、员工管理的基本功能,但是大家会发现,我们并没有登录,就直接访问到了Tlias智能…...

6.1 内存模式概述
Bruce Powel Douglass大师介绍-CSDN博客 嵌入式软件开发从小工到专家-CSDN博客 C嵌入式编程设计模式源码-CSDN博客 “内存管理模式”介绍了几种内存管理的模式,每种模式都针对特定的系统需求和约束设计。 6.2 静态分配模式(Static Allocation Patter…...

Python中容器类型的数据
目录 序列 序列的索引操作 加和乘操作 切片操作 成员测试 列表 创建列表 追加元素 插入元素 替换元素 删除元素 元组 创建元组 元组拆包 集合 创建集合 修改集合 字典 创建字典 修改字典 访问字典视图 遍历字典 若我们想将多个数据打包并且统一管理&…...
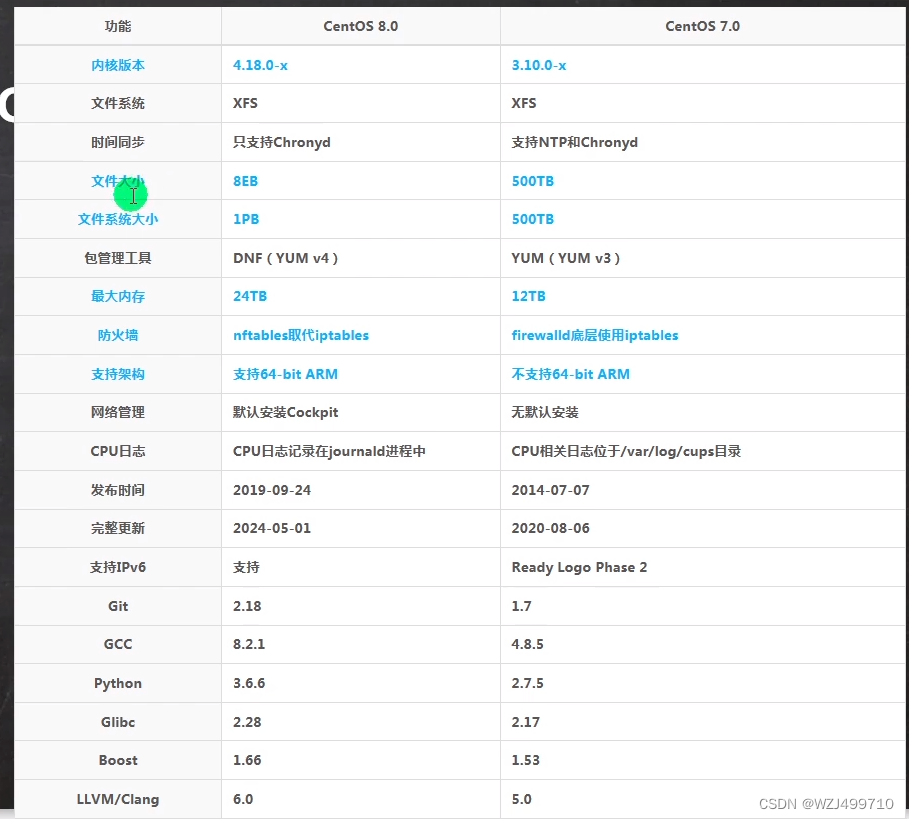
虚拟机安装Centos8.5
记得看目录哦! 附件1. 新建虚拟机2. 安装Centos8.5 附件 安装包自行下载 https://mirrors.aliyun.com/centos/8/isos/x86_64/ 1. 新建虚拟机 2. 安装Centos8.5 启动虚拟机–选择第一个install Centos8.5 记得接收许可证...

ENVI下基于知识决策树提取地表覆盖信息
基于知识的决策树分类是基于遥感影像数据及其他空间数据,通过专家经验总结、简单的数学统计和归纳方法等,获得分类规则并进行遥感分类。分类规则易于理解,分类过程也符合人的认知过程,最大的特点是利用的多源数据。 决策树分类主要的工作是获取规则,本文介绍使用CART算法…...
arco design table遇到的一些问题
问题1:不知情就成了树形table table中不知道为啥就多了个树形加号在前面,查找问题后发现,是后端返回的数据中有children,框架中默认对这个参数做了树形结构。 解决办法: 当时没找到取消或者修改字段的属性或方法&…...

Linux系统——文本三剑客
目录 一、grep 1.格式 2.选项 2.1 grep重定向 2.2grep -m 匹配到几次停止 2.3grep -i 忽略大小写 2.4grep -n 显示行号 2.5grep -c 统计匹配行数 2.6grep -A 后几行 2.7grep -C 前后三行 2.8grep -B 前三行 2.9grep -e 或 2.10grep -w 匹配整个单词 2.11grep -r…...

代码随想录算法训练营Day38|动态规划理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
目录 动态规划理论基础 什么是动态规划 动态规划的解题步骤 动态规划的debug 509. 斐波那契数 前言 思路 算法实现 方法一:动态规划 方法二:递归法 70. 爬楼梯 前言 思路 算法实现 拓展 746. 使用最小花费爬楼梯 算法实现 总结 动态规划…...

C++中的指针空值nullptr
一、nullptr的引入 在C98中,通常是用NULL或者0对指针变量进行初始化 int* p1 NULL; int* p2 0; NULL其实一个宏,本质是0,在传统C头文件stddef.h中给可以看到如下代码 #ifndef NULL #ifdef __cplusplus #define NULL 0 #else #define …...
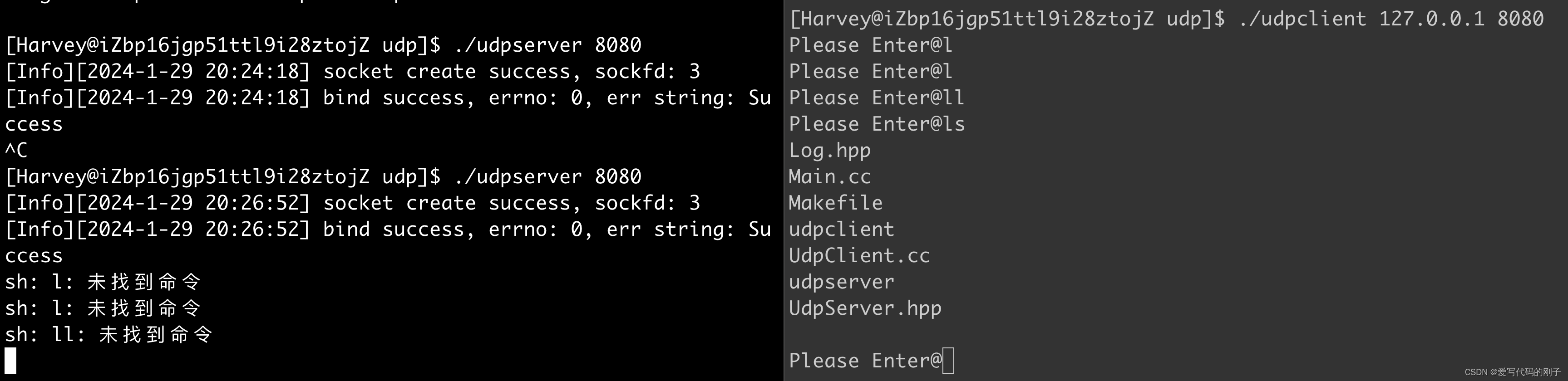
【Linux网络编程】网络编程套接字(1)
【Linux网络编程】网络编程套接字(1) 目录 【Linux网络编程】网络编程套接字(1)源IP地址和目的IP地址端口号端口号和进程ID的关系 网络通信TCP协议UDP协议网络字节序socket编程接口简单的UDP网络程序 作者:爱写代码的刚子 时间:2024.1.29 前言࿱…...
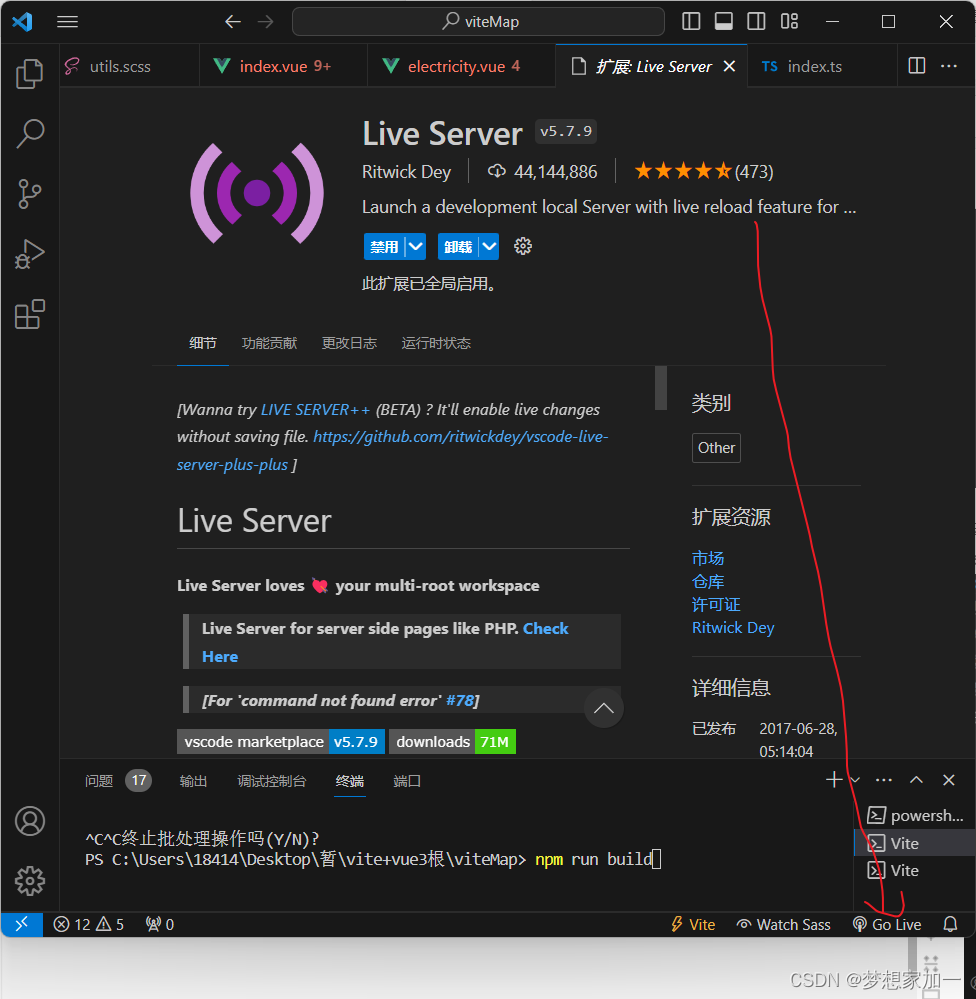
vite+ts+vue3打包的过程和错误
文章目录 概要vite.config.ts配置tsconfig.json 的配置package.json 的配置路由配置打包打开打包后的文件小结 概要 完成vite的打包,和在本地打开页面 记录一下,vite打包过程中的问题!!! vite.config.ts配置 vite.config.ts配置打包的相关配置 import…...
-面试经典150题)
80.双指针实现删除有序数组中的重复项 II(中等)-面试经典150题
题目 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。 说明…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
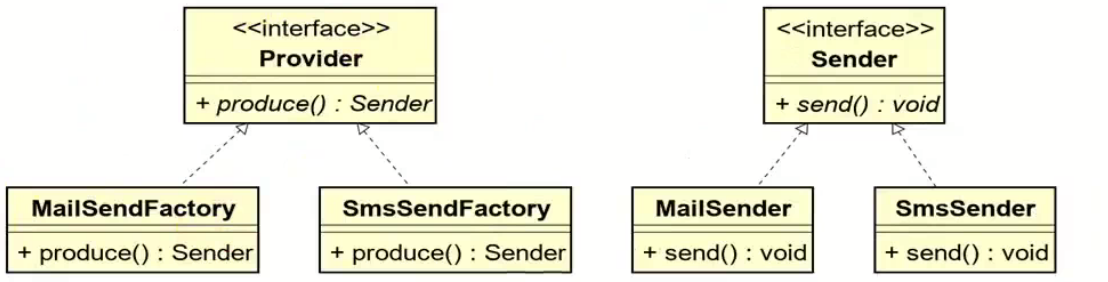
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
