西瓜书学习笔记——层次聚类(公式推导+举例应用)
文章目录
- 算法介绍
- 实验分析
算法介绍
层次聚类是一种将数据集划分为层次结构的聚类方法。它主要有两种策略:自底向上和自顶向下。
其中AGNES算法是一种自底向上聚类算法,用于将数据集划分为层次结构的聚类。算法的基本思想是从每个数据点开始,逐步合并最相似的簇,直到形成一个包含所有数据点的大簇。这个过程被反复执行,构建出一个层次化的聚类结构。这其中的关键就是如何计算聚类簇之间的距离。 但实际上,每个簇都是一个集合,故我们只需要计算集合与集合的距离即可。例如,给定聚类簇 C i C_i Ci与 C j C_j Cj,可通过下面的式子来计算距离:
d m i n ( C i , C j ) = min x ∈ C i , z ∈ C j d i s t ( x , z ) (1) d_{min}(C_i,C_j)=\underset{x \in C_i,z\in C_j}{\text{min}} \ dist(x,z) \tag{1} dmin(Ci,Cj)=x∈Ci,z∈Cjmin dist(x,z)(1)
d m a x ( C i , C j ) = max x ∈ C i , z ∈ C j d i s t ( x , z ) (2) d_{max}(C_i,C_j)=\underset{x \in C_i,z\in C_j}{\text{max}} \ dist(x,z) \tag{2} dmax(Ci,Cj)=x∈Ci,z∈Cjmax dist(x,z)(2)
d a v g ( C i , C j ) = 1 ∣ C i ∣ ∣ C j ∣ ∑ x ∈ C i ∑ z ∈ c j d i s t ( x , z ) (3) d_{avg }(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum_{x\in C_i}\sum_{z\in c_j} dist(x,z) \tag{3} davg(Ci,Cj)=∣Ci∣∣Cj∣1x∈Ci∑z∈cj∑dist(x,z)(3)
其中 ∣ C i ∣ |C_i| ∣Ci∣是集合 C i C_i Ci的元素个数。显然最小距离是由两个簇最近的样本点决定的;最大距离是由两个簇最远的样本点决定的;平均距离是由两个簇所有样本点共同决定的。
还有个更有效的计算集合距离的方法豪斯多夫距离:假设在同一样本空间的集合 X X X与 Z Z Z之间的距离可以通过以下式子计算:
dist H ( X , Z ) = max ( dist h ( X , Z ) , dist h ( Z , X ) ) (4) \operatorname{dist}_{\mathrm{H}}(X, Z)=\max \left(\operatorname{dist}_{\mathrm{h}}(X, Z), \operatorname{dist}_{\mathrm{h}}(Z, X)\right) \tag{4} distH(X,Z)=max(disth(X,Z),disth(Z,X))(4)
其中 dist h ( X , Z ) = max x ∈ X min z ∈ Z ∥ x − z ∥ 2 \operatorname{dist}_{\mathrm{h}}(X, Z)=\max _{\boldsymbol{x} \in X} \min _{\boldsymbol{z} \in Z}\|\boldsymbol{x}-\boldsymbol{z}\|_2 disth(X,Z)=maxx∈Xminz∈Z∥x−z∥2
豪斯多夫距离的应用涉及到形状匹配、图像匹配、模式识别等领域,它对于描述两个集合的整体形状之间的差异具有较好的效果。然而,由于计算豪斯多夫距离涉及到点之间的一一匹配,因此在实际应用中可能需要考虑一些优化算法以提高计算效率。
下图是AGNES算法流程图:

实验分析
数据集如下表所示:
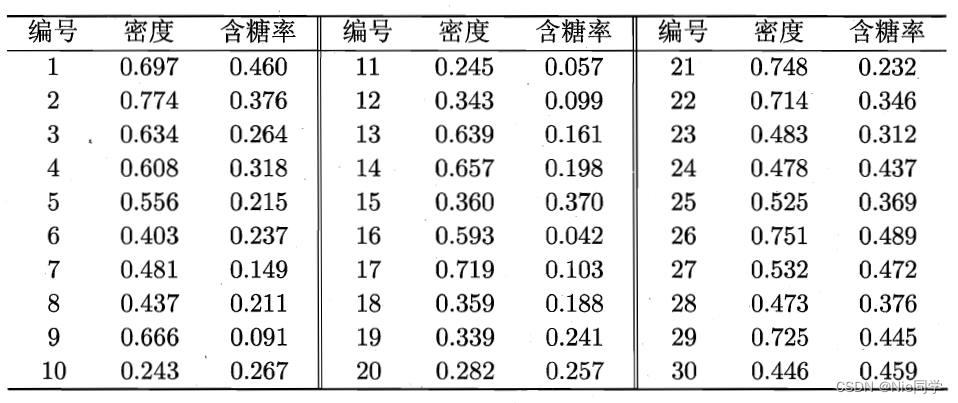
读入数据集:
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltdata = pd.read_csv('data/4.0.csv')
定义距离函数:
# 定义豪斯多夫距离函数
def hausdorff_distance(cluster1, cluster2):max_distance1 = max(min(distance(p1, p2) for p1 in cluster1) for p2 in cluster2)max_distance2 = max(min(distance(p1, p2) for p2 in cluster2) for p1 in cluster1)return max(max_distance1, max_distance2)# 定义距离函数
def distance(point1, point2):return ((point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2) ** 0.5
AGNES算法:
# AGNES算法
def agnes(data):clusters = [[point] for point in data.values]while len(clusters) > 4:min_distance = float('inf')merge_indices = (0, 0)for i in range(len(clusters)):for j in range(i + 1, len(clusters)):cluster1 = clusters[i]cluster2 = clusters[j]current_distance = hausdorff_distance(cluster1, cluster2)if current_distance < min_distance:min_distance = current_distancemerge_indices = (i, j)# 合并最近的两个簇merged_cluster = clusters[merge_indices[0]] + clusters[merge_indices[1]]clusters.pop(merge_indices[1])clusters[merge_indices[0]] = merged_clusterreturn clusters
绘制分类结果函数:
# 绘制分类结果
def plot_clusters(data, clusters):plt.figure(figsize=(8, 8))# 绘制原始数据点plt.scatter(data['Density'], data['Sugar inclusion rate'], color='black', label='Original Data')# 绘制分类结果for i, cluster in enumerate(clusters):cluster_data = pd.DataFrame(cluster, columns=['Density', 'Sugar inclusion rate'])plt.scatter(cluster_data['Density'], cluster_data['Sugar inclusion rate'], label=f'Cluster {i + 1}')# 添加标签和图例plt.title('AGNES Clustering Result')plt.xlabel('Density')plt.ylabel('Sugar inclusion rate')plt.legend()plt.show()
执行AGNES且画出分类结果:
# 执行层次聚类
result_clusters = agnes(data)# 输出聚类结果
for i, cluster in enumerate(result_clusters):print(f'Cluster {i + 1}: {cluster}')# 绘制分类结果图
plot_clusters(data, result_clusters)
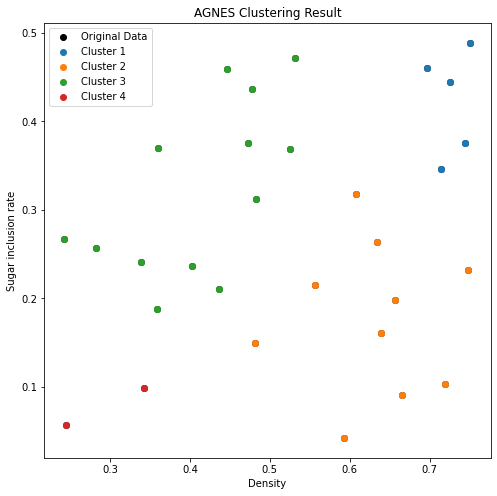
相关文章:

西瓜书学习笔记——层次聚类(公式推导+举例应用)
文章目录 算法介绍实验分析 算法介绍 层次聚类是一种将数据集划分为层次结构的聚类方法。它主要有两种策略:自底向上和自顶向下。 其中AGNES算法是一种自底向上聚类算法,用于将数据集划分为层次结构的聚类。算法的基本思想是从每个数据点开始࿰…...
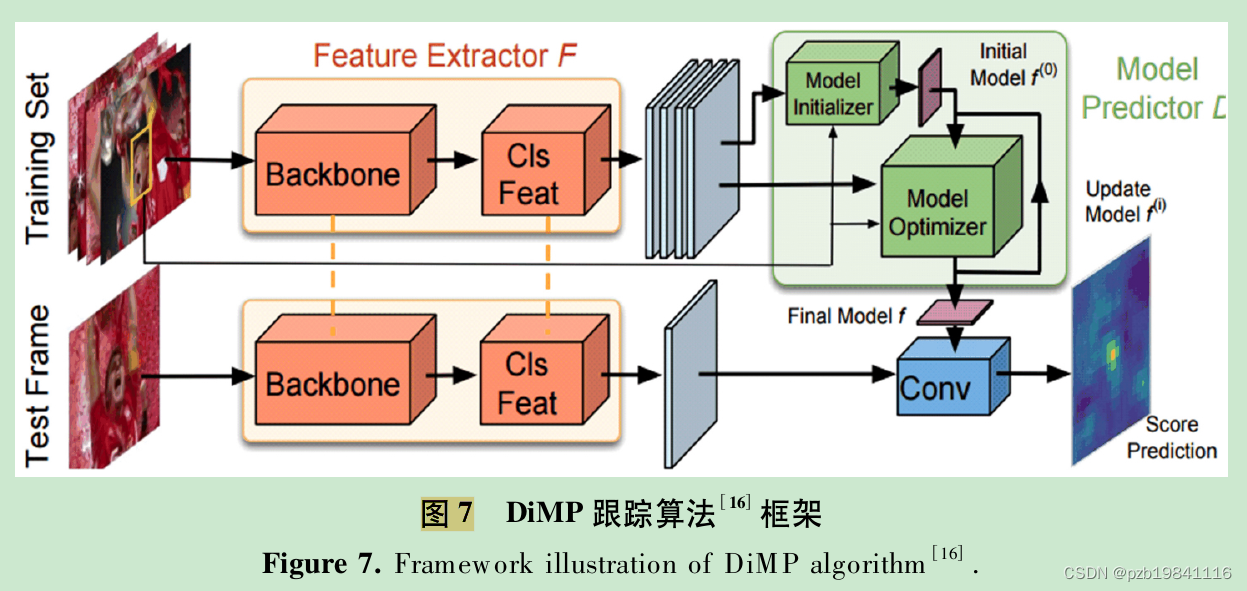
深度视觉目标跟踪进展综述-论文笔记
中科大学报上的一篇综述,总结得很详细,整理了相关笔记。 1 引言 目标跟踪旨在基于初始帧中指定的感兴趣目标( 一般用矩形框表示) ,在后续帧中对该目标进行持续的定位。 基于深度学习的跟踪算法,采用的框架包括相关滤波器、分类…...

【数据结构:顺序表】
文章目录 线性表顺序表1.1 顺序表结构的定义1.2 初始化顺序表1.3 检查顺序表空间1.4 打印1.5 尾插1.6 头插1.7 尾删1.8 头删1.9 查找1.10 指定位置插入1.11 删除指定位置数据1.12 销毁顺序表 数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一…...

android tts播报破音解决方案汇总
导航app引导中经常遇到破音,这里也将之前经历过的方案收集以下,方便以后选择: 1 对于开始和结尾破音: 可以用升降音来处理 两种方式 一种是 直接对开始和结束的时间段进行音量直接渐进改变。这里配的是200ms的渐变。 VolumeSha…...

2024年新提出的算法:一种新的基于数学的优化算法——牛顿-拉夫森优化算法|Newton-Raphson-based optimizer,NRBO
1、简介 开发了一种新的元启发式算法——Newton-Raphson-Based优化器(NRBO)。NRBO受到Newton-Raphson方法的启发,它使用两个规则:Newton-Raphson搜索规则(NRSR)和Trap Avoidance算子(TAO&#…...

笔记 | Clickhouse 命令行连接及查询
在 ClickHouse 中,可以使用命令行客户端执行查询。默认情况下,ClickHouse 的命令行客户端称为 clickhouse-client。下面是一些基本的步骤和示例,用于使用 clickhouse-client 进行查询。 首先,需要确保已经安装了 ClickHouse 服务…...

设计模式—行为型模式之责任链模式
设计模式—行为型模式之责任链模式 责任链(Chain of Responsibility)模式:为了避免请求发送者与多个请求处理者耦合在一起,于是将所有请求的处理者通过前一对象记住其下一个对象的引用而连成一条链;当有请求发生时&am…...
如何使用Python+Flask搭建本地Web站点并结合内网穿透公网访问?
文章目录 前言1. 安装部署Flask并制作SayHello问答界面2. 安装Cpolar内网穿透3. 配置Flask的问答界面公网访问地址4. 公网远程访问Flask的问答界面 前言 Flask是一个Python编写的Web微框架,让我们可以使用Python语言快速实现一个网站或Web服务,本期教程…...

【C语言】【力扣】刷题小白的疑问
一、力扣做题时的答案,没有完整的框架 疑问: 在学习C语言的初始,就知道C语言程序离不开下面这个框架,为什么力扣题的解答往往没有这个框架? #include <stdio.h>int main() {return 0; } 解答: 力扣平…...
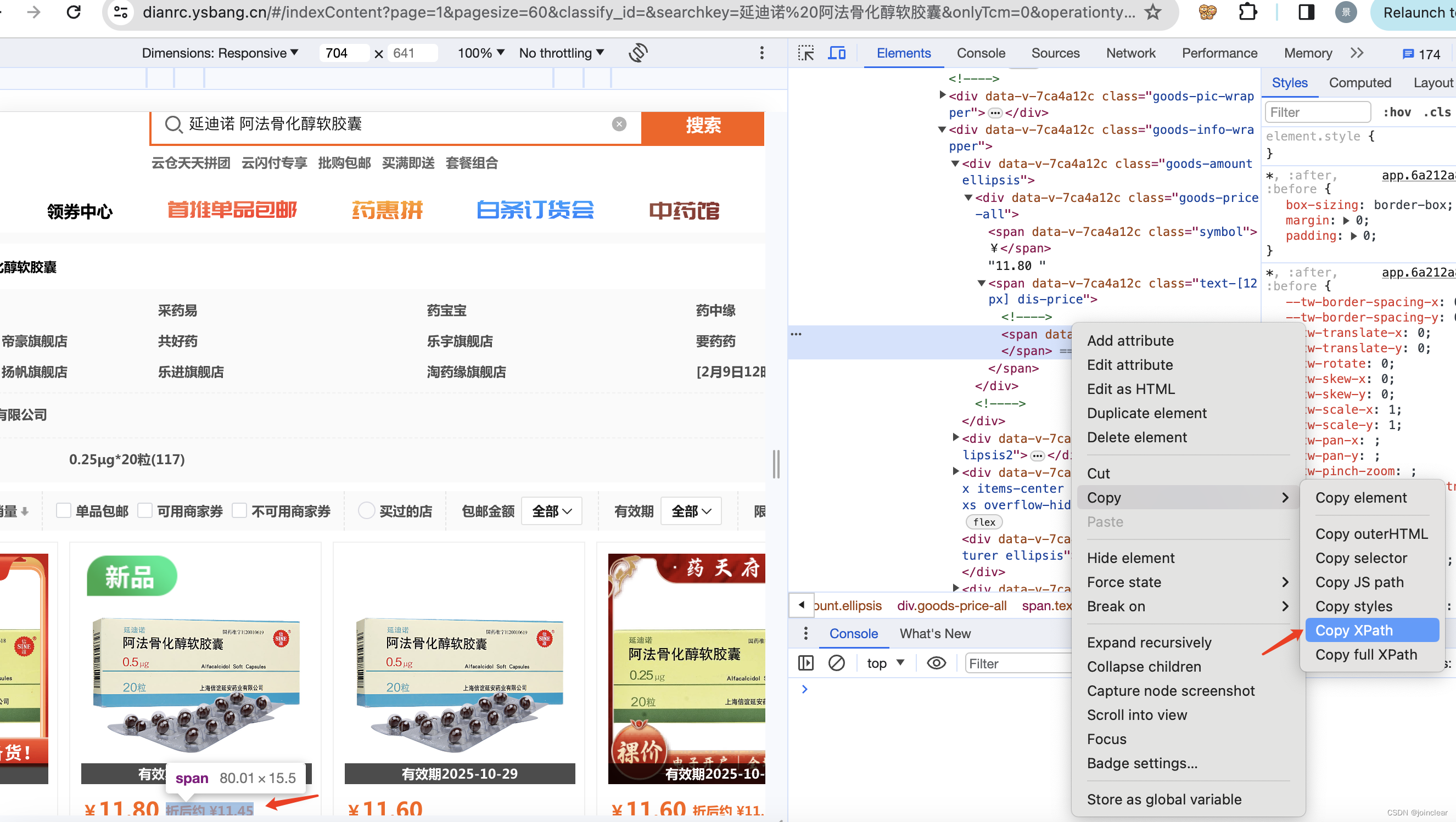
【Python】03快速上手爬虫案例三:搞定药师帮
文章目录 前言1、破解验证码2、获取数据 前言 提示:通过用户名、密码、搞定验证码,登录进药师帮网站,然后抓取想要的数据。 爬取数据,最终效果图: 1、破解验证码 使用药师帮测试系统:https://dianrc.ysb…...

C++异步编程
thread std::thread 类代表一个单独的执行线程。在创建与线程对象相关联时,线程会立即开始执行(在等待操作系统调度的延迟之后),从构造函数参数中提供的顶层函数开始执行。顶层函数的返回值被忽略,如果它通过抛出异常…...
P1141 01迷宫——洛谷(题解))
dfs专题(记忆化搜索)P1141 01迷宫——洛谷(题解)
题目描述 有一个仅由数字 00 与 11 组成的 ��nn 格迷宫。若你位于一格 00 上,那么你可以移动到相邻 44 格中的某一格 11 上,同样若你位于一格 11 上,那么你可以移动到相邻 44 格中的某一格 00 上。 你的任务是&#…...
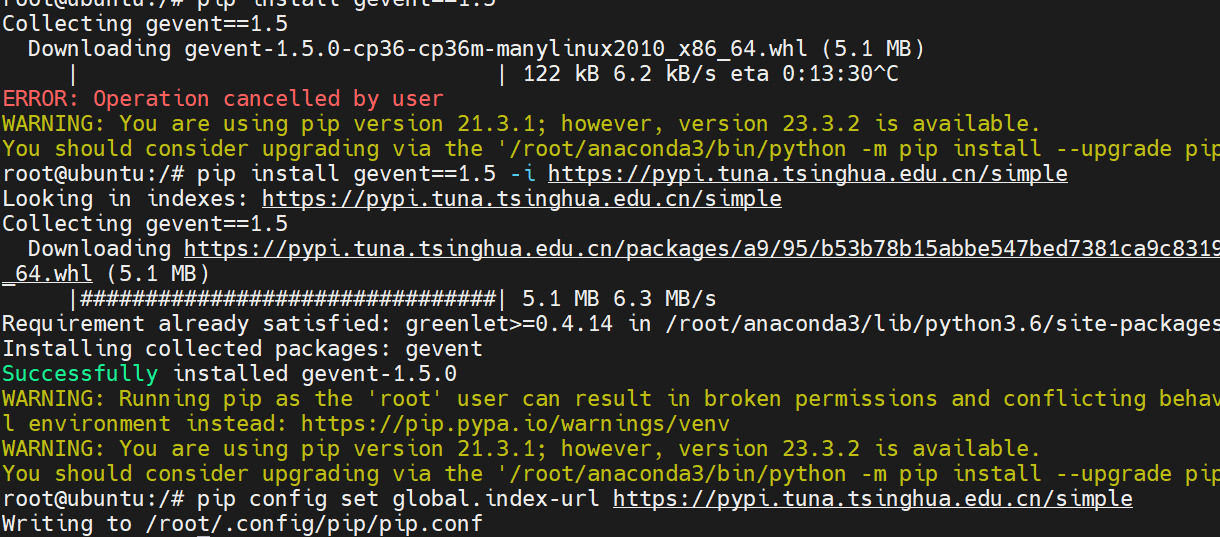
pip 安装出现报错 SSLError(SSLError(“bad handshake
即使设置了清华源: pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simplepip 安装包不能配置清华源,出现报错: Retrying (Retry(total2, connectNone, readNone, redirectNone, statusNone)) after connection broken by ‘SSLE…...
)
新概念英语第二册(46)
【New words and expressions】生词和短语(12) unload v. 卸(货) wooden adj. 木制的 extremely adv. 非常,极其 occur …...

动态规划入门题目
动态规划(记忆化搜索): 将给定问题划分成若干子问题,直到子问题可以被直接解决。然后把子问题的答保存下来以免重复计算,然后根据子问题反推出原问题解的方法 动态规划也称为递推(暴力深搜记忆中间状态结果…...

探索云性能测试的各项功能有哪些?
云性能测试作为现代软件开发和部署过程中不可或缺的一环,为确保系统在各种条件下的高效运行提供了关键支持。本文将介绍云性能测试的各项功能,帮助您更好地了解其在软件开发生命周期中的重要性。 1. 负载测试 云性能测试的首要功能之一是负载测试。通过模…...
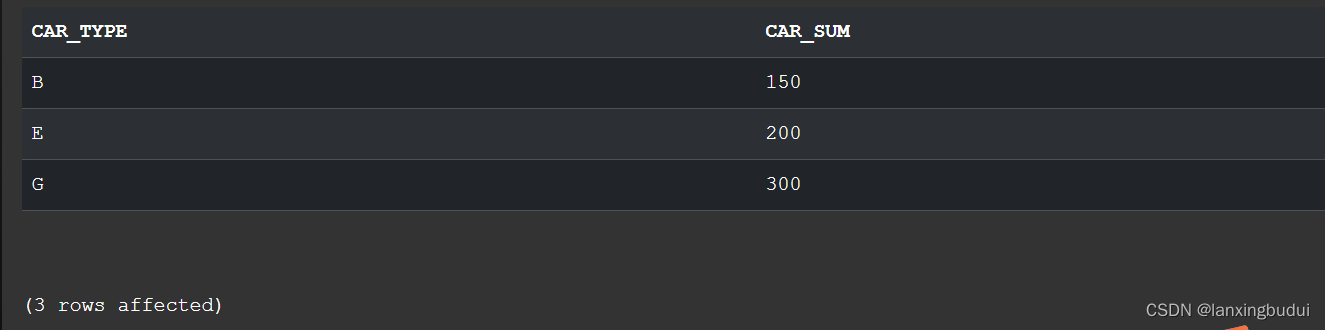
(大众金融)SQL server面试题(1)-总销售量最少的3个型号的车及其总销售量
今天,面试了一家公司,什么也不说先来三道面试题做做,第一题。 那么,我们就开始做题吧,谁叫我们是打工人呢。 题目是这样的: 统计除豪车外,销售最差的车 车辆按批销售,每次销售若干…...
Git安装,Git镜像,Git已安装但无法使用解决经验
git下载地址: Git - 下载 (git-scm.com) <-git官方资源 Git for Windows (github.com) <-github资源 CNPM Binaries Mirror (npmmirror.com) <-阿里镜像(推荐,镜…...
分类提取坐标到excel(补充圆半径、线长度、圆弧))
Python与CAD系列高级篇(二十五)分类提取坐标到excel(补充圆半径、线长度、圆弧)
目录 0 简述1 分类提取坐标到excel2 结果展示0 简述 上一篇中介绍了:对点、直线、多段线、圆、样条曲线分类读取坐标并提取到excel。考虑到进一步提取图形信息,此篇补充对圆半径、线长度以及圆弧几何信息的提取。 1 分类提取坐标到excel 代码实现: import math import nump…...

Linux安装Influxdb
Linux安装Influxdb 1、安装步骤1.1、安装Influxdb步骤1.2、Influxdb默认安装路径1.3、命令行操作Influxdb,建库,建用户1.3.1 进入influxdb命令行1.3.2 创建用户1.3.2 库查询和创建 1、安装步骤 1.1、安装Influxdb步骤 yum install -y wget #下载安装包…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...

篇章一 论坛系统——前置知识
目录 1.软件开发 1.1 软件的生命周期 1.2 面向对象 1.3 CS、BS架构 1.CS架构编辑 2.BS架构 1.4 软件需求 1.需求分类 2.需求获取 1.5 需求分析 1. 工作内容 1.6 面向对象分析 1.OOA的任务 2.统一建模语言UML 3. 用例模型 3.1 用例图的元素 3.2 建立用例模型 …...
