逻辑优化-rewrite
简介
逻辑综合中的rewrite算法是一种常见的优化算法,其主要作用是通过对逻辑电路的布尔函数进行等效变换,从而达到优化电路面积、时序和功耗等目的。本文将对rewrite算法进行详细介绍,并附带Verilog代码示例。
一、算法原理
rewrite算法的核心思想是通过布尔代数中的等价变换来达到电路优化的目的。具体而言,算法将电路的原始布尔函数通过一系列等价变换转化为更简单的布尔函数,从而达到优化的目的。
二、算法流程
rewrite算法的流程如下所示:
- 输入电路的原始布尔函数;
- 根据规则库中定义的等价变换规则,将原始布尔函数转化为一个或多个新的布尔函数;
- 对新的布尔函数重复上述步骤,直到布尔函数无法继续化简为止;
- 输出化简后的布尔函数。
具体来说,rewrite算法通过一系列等价变换规则将布尔函数转化为其等效的形式,如下所示:
同一律: A+A=A; A*1=A;
零元素: A+0=A; A*0=0;
吸收律: A+AB=A; A(A+B)=A;
分配律: A*(B+C)=AB+AC;
德摩根定律: ~(A+B)=~A~B; ~(AB)=~A+~B;
布尔恒等式: A+~A=1; A*~A=0;
交换律: A+B=B+A; AB=BA;
结合律: A+(B+C)=(A+B)+C; A*(BC)=(AB)*C;
分配律的逆定理: (A+B)C=(AC)+(B*C);
吸收律的逆定理: A+(AB)=A; A(A+B)=A。
通过这些等价变换规则,rewrite算法可以将一个布尔函数化简为其最简形式,从而达到电路优化的目的。
3. 示例
假设我们有一个简单的逻辑电路,其功能等价于两个输入a和b做异或运算,输出结果为c:
module xor_gate(input a, b, output c);assign c = a ^ b;
endmodule我们可以使用逻辑综合中的rewrite算法对这个电路进行优化,从而得到一个更为简单的电路。
具体来说,我们可以应用一个rewrite规则:将异或门替换为两个AND门、一个OR门和两个NOT门的等效电路。下面是应用这个规则后的Verilog代码:
module xor_to_and_or(input a, b, output c);wire not_a, not_b, and_a_b, and_not_a_not_b, or_a_b;assign not_a = ~a;assign not_b = ~b;assign and_a_b = a & b;assign and_not_a_not_b = not_a & not_b;assign or_a_b = and_not_a_not_b | and_a_b;assign c = ~or_a_b;
endmodule然后,我们可以在原始的xor_gate模块中,使用新的xor_to_and_or模块来实现优化后的电路,如下所示:
module xor_gate(input a, b, output c);xor_to_and_or rule(.a(a), .b(b), .c(c));
endmodule通过这个优化,我们将一个异或门转化为了两个AND门、一个OR门和两个NOT门的电路结构,从而实现了对电路的优化,事实上这是一个反向的优化。当然,这只是一个简单的例子,实际应用中rewrite算法的规则和应用方法可能会更加复杂和多样化,需要根据具体的设计需求和约束来确定。同时,需要注意电路优化可能会对电路的性能、功耗、可靠性等方面产生影响,需要进行综合分析和评估。
相关文章:

逻辑优化-rewrite
简介 逻辑综合中的rewrite算法是一种常见的优化算法,其主要作用是通过对逻辑电路的布尔函数进行等效变换,从而达到优化电路面积、时序和功耗等目的。本文将对rewrite算法进行详细介绍,并附带Verilog代码示例。 一、算法原理 rewrite算法的…...
文件传输与聊天系统设计
技术:Java等摘要:本文介绍了一种基于TCP/IP协议使用Socket技术实现的聊天室系统,包括私聊功能和文件传输功能,对系统的主要模块进行了分析,并对系统实现过程中遇到的关键性技术进行了阐述,最后对系统进行了…...
蓝桥杯第十四届校内赛(第三期) C/C++ B组
一、填空题 (一)最小的十六进制 问题描述 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个数的十进制形式作…...

有关平方或高次方的公式整理一元高次方程的求解
Part.I Introduction 这篇博文记录一下数学中常用的有关平方或高次方的一些公式。 Chap.I 一些结论 下面一部分汇总了一些重要的结论 完全平方公式:(ab)2a22abb2(ab)^2a^22abb^2(ab)2a22abb2平方差公式:a2−b2(ab)(a−b)a^2-b^2(ab)(a-b)a2−b2(ab)(…...

Java笔记3
ArrayListArrayList<String> list new Arraylist<>();<>是泛型表示存放的数据类型,注意不能是基本数据类型;增删改查增:add 返回值为true删:remove 1.直接删元素2.根据索引删元素改:set(…...

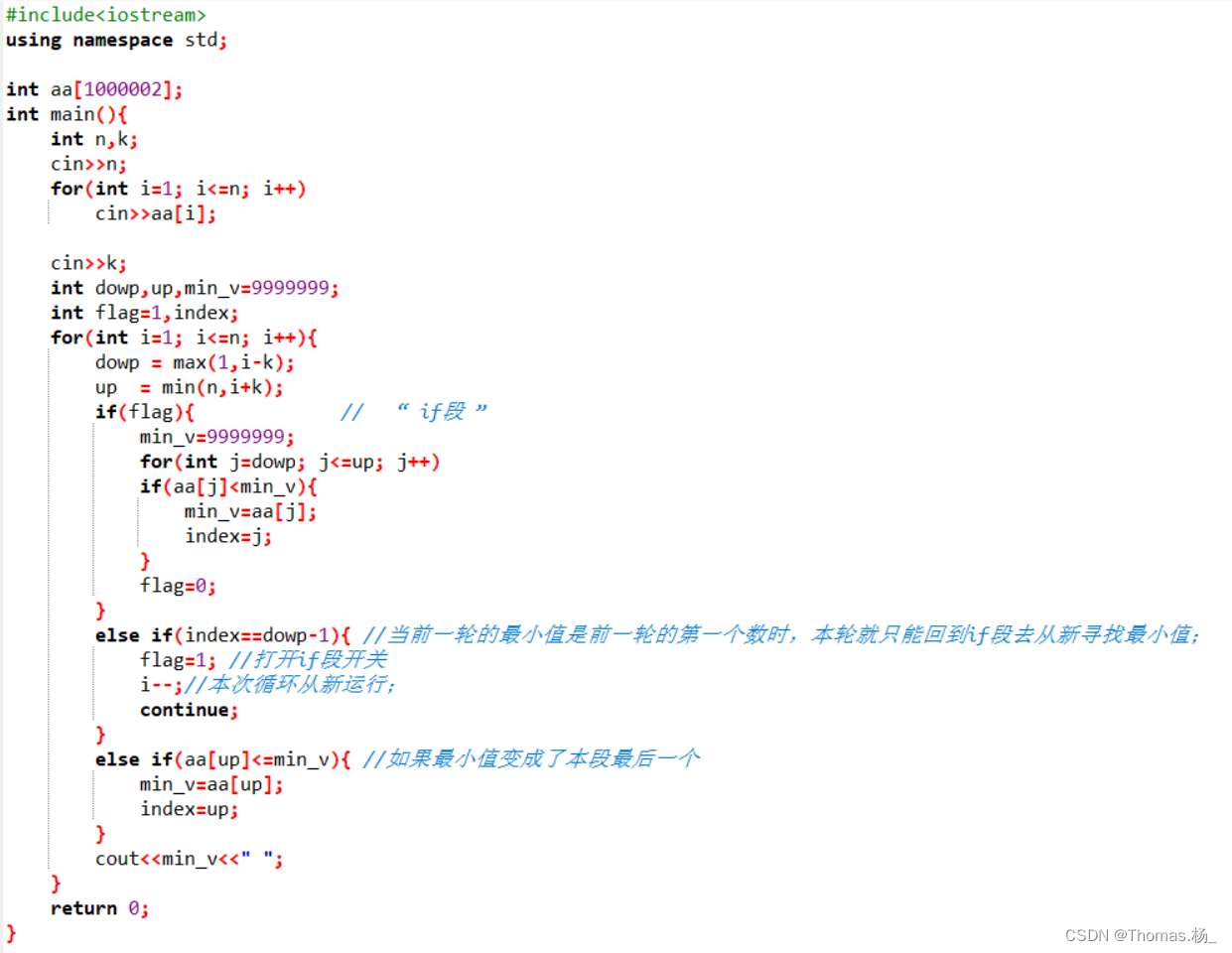
Leetcode.2202 K 次操作后最大化顶端元素
题目链接 Leetcode.2202 K 次操作后最大化顶端元素 Rating : 1717 题目描述 给你一个下标从 0开始的整数数组 nums,它表示一个 栈 ,其中 nums[0]是栈顶的元素。 每一次操作中,你可以执行以下操作 之一 : 如果栈非空…...

JAVA知识点全面总结3:String类的学习
三.String类学习 1.String,StringBuffer,StringBuilder的区别? 2.字符串拼接用加号的原理 ? 3.字符串常量池如何理解? 4.String的intern方法理解? 5.String的equals方法和compareTo方法的使用…...
Eureka注册中心和Nacos注册中心详解以及Nacos与Eureka有什么区别?
目录:前言Eureka注册中心Nacos注册中心Nacos与Eureka有什么区别?前言提供接口给其它微服务调用的微服务叫做服务提供者,而调用其它微服务提供的接口的微服务则是服务消费者。如果服务A调用了服务B,而服务B又调用了服务C࿰…...

Web3D发展趋势以及Web3D应用场景
1,Web3D发展趋势随着互联网的快速发展,Web3D技术也日渐成熟,未来发展趋势也值得关注。以下是Web3D未来发展趋势的七个方面:可视化和可交互性的增强:Web3D可以为三维数据提供可视化和可交互性的增强,将极大地…...

2023-3-4 刷题情况
按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length 0 < j < nums.length 0 < k < nums.l…...
前端面试总结
1.引言 最近参加了大量的招聘会,投递了大量的简历,整整体会了从“随便找个厂上一下”——“还是的找个大厂”——“没人要”——“急了急了,海投一波”——“工资有点尬”——“海投中…”。简单说一下自己的一些感受吧,现在的前端属实有点尴…...
: Spatial clustering)
Geospatial Data Science (6): Spatial clustering
Geospatial Data Science (6): Spatial clustering 1.Clustering, spatial clustering, and geodemographics 本节涉及空间观测的统计聚类。许多问题和主题都是复杂的现象,涉及多个维度,难以归纳为一个单一的变量。在统计学术语中,我们把这一类问题称为多变量,而不是在…...

蚁群算法优化问题
%%%%%%%%%%%%蚁群算法解决 TSP 问题%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%% clear all; %清除所有变量 close all; %清图 clc; %清屏 m 50; %蚂蚁个数 Alpha 1; %信息素重要程度参数 Beta 5; %启发式因子重要程度参数 Rho 0.1; %信息素蒸发系数 G 20…...

为啥一个 main 方法就能启动项目
在 Spring Boot 出现之前,我们要运行一个 Java Web 应用,首先需要有一个 Web 容器(例如 Tomcat 或 Jetty),然后将我们的 Web 应用打包后放到容器的相应目录下,最后再启动容器。 在 IDE 中也需要对 Web 容器…...

洛谷:P1554 梦中的统计 JAVA
思路:定义一个长度为10的数组,数组下标代表数组元素的数字,比如arr[0]代表数字0.用一个for循环,对每个数先取余再取整,知道取整得到的数为0,说明该数字已经被拆解完了。今天又学了一个输入,原来…...
C++初学笔记整理
目录 1. C关键字 2. 命名空间 1)命名空间的引入和概述 2)命名空间的定义 3)std与命名空间的使用 4).相关特性 3. C输入&输出 4. 缺省参数 1 )缺省参数概念 2)使用及分类 a.全缺省 b.部分缺省 5. 函数…...

记录--在Vue3这样子写页面更快更高效
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 前言 在开发管理后台过程中,一定会遇到不少了增删改查页面,而这些页面的逻辑大多都是相同的,如获取列表数据,分页,筛选功能这些基本功能。而…...
】测验和作业题部分答案汇总(面向对象篇))
【程序设计与算法(三)】测验和作业题部分答案汇总(面向对象篇)
题目来源:程序设计与算法(三)测验和作业题汇总 文章目录001:简单的swap002:难一点的swap003:好怪异的返回值004:神秘的数组初始化005:编程填空:学生信息处理程序006:奇怪的类复制007:返回什么才好呢008:超简单的复数类009:哪来的输…...
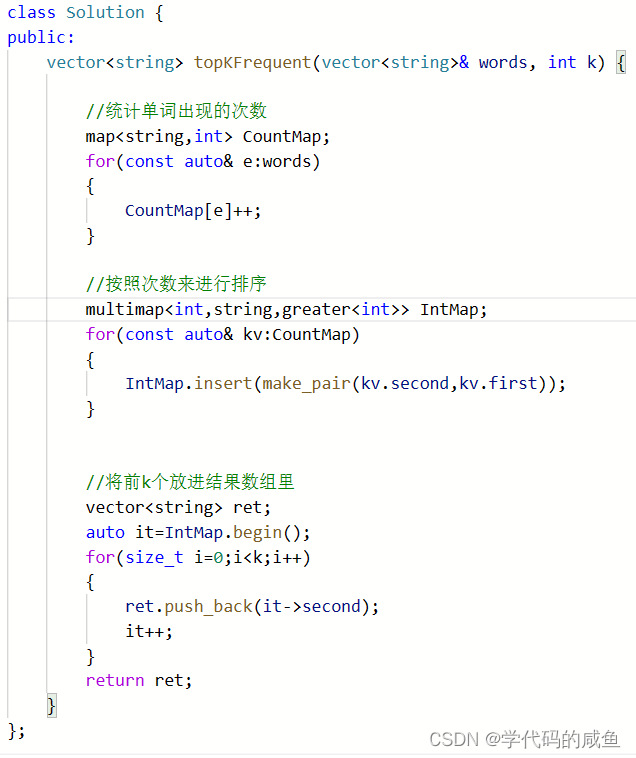
LeetCode 349. 两个数组的交集和 692. 前K个高频单词
两个数组的交集 难度 简单 题目链接 这道题的难度不大,我们可以把数组里的数据存到set里面。这样就完成了排序和去重,然后我们再把一个set里面的数据和另外一个set数据进行比较。如果相同就插入到数组里。 代码如下: 但是这个算法的时间复…...
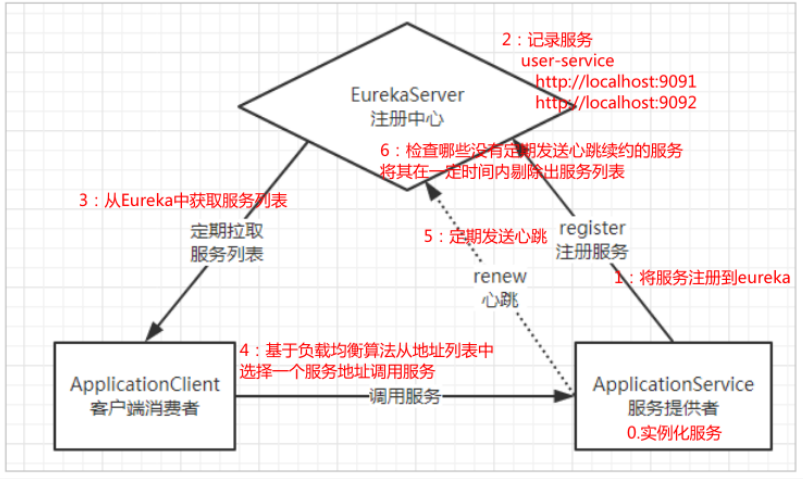
SpringCloud的五大组件功能
SpringCloud的五大组件 EurekaRibbonHystrixZuulConfig 一、Eureka 作用是实现服务治理,即服务注册与发现。 Eureka服务器相当于一个中介,负责管理、记录服务提供者的信息。服务调用者不需要自己寻找服务 ,而是把需求告诉Eureka &#x…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
