Day39 62不同路径 63不同路径II 343整数拆分 96不同的二叉搜索树
62 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

- 输入:m = 3, n = 7
- 输出:28
示例 2:
- 输入:m = 2, n = 3
- 输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向右 -> 向下
- 向右 -> 向下 -> 向右
- 向下 -> 向右 -> 向右
本题用动态规划五部曲进行分析:首先dp数组的含义是到达这个点有多少种走法,这里题目已经给了按时,递推方程为左边的走法加上面的走法,即dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; 初始条件为左边界和上边界都初始为1,选择两个边界是因为只有通过这样才能让后面的dp数组有值,选择1是因为每次走到那里都是一种走法;遍历顺序为从前往后依次遍历,最后打印dp数组:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};63 不同路径II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
本题相比于上一题,主要就是添加了障碍,如果障碍在起始或者终止位置,直接返回0即可,如果在左边界和上边界,障碍和后面的所有dp都设为0即可,在网格中,一旦遇到了障碍,就跳过他:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};343 整数拆分
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
递归五部曲:首先dp数组表示的就是最大乘积,递推公式为dp[i]=max(dp[i], max((i-j)*j,dp[i-j]*j));
初始条件只能从2开始取,拆分以后最大乘积为1,遍历顺序从前到后:
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};96 不同的二叉搜索树
给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种?

本题经过测试发现,后面的搜索树的数量和前面的搜索树的数量是有关系的,因为这是一个二叉搜索树,
在上面的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
};
相关文章:

Day39 62不同路径 63不同路径II 343整数拆分 96不同的二叉搜索树
62 不同路径 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径&#…...

JavaScript 的 ~~ 运算和floor 的性能差异
在JavaScript中,~~(双波浪号)和Math.floor()都可以用于向下取整,但它们在行为和性能上有一些差异。要测试这两者之间的性能差异,你可以使用JavaScript的performance.now()方法来进行基准测试。 行为差异 Math.floor()…...
AtCoder Beginner Contest 338F - Negative Traveling Salesman【floyd+状态压缩dp】
原题链接:https://atcoder.jp/contests/abc338/tasks/abc338_f Time Limit: 6 sec / Memory Limit: 1024 MB Score: 500 points、 问题陈述 有一个有N个顶点和M条边的加权简单有向图。顶点的编号为 1 到 N,i/th 边的权重为 Wi,从顶点 U…...
UDP/TCP协议特点
1.前置知识 定义应用层协议 1.确定客户端和服务端要传递哪些信息 2.约定传输格式 网络上传输的一般是二进制数据/字符串 结构化数据转二进制/字符串 称为序列化 反之称之为反序列化 下面就是传输层了 在TCP/IP协议中,我们以 目的端口,目的IP 源端口 源IP 协议号这样一个五…...

编程笔记 html5cssjs 059 css多列
编程笔记 html5&css&js 059 css多列 一、CSS3 多列属性二、实例小结 CSS3 可以将文本内容设计成像报纸一样的多列布局. 一、CSS3 多列属性 下表列出了所有 CSS3 的多列属性: 属性 描述 column-count 指定元素应该被分割的列数。 column-fill 指定如何填充…...

Facebook的元宇宙探索:虚拟社交的新时代
近年来,科技的飞速发展推动着人类社交方式的翻天覆地的改变。在这场数字化革命的浪潮中,社交媒体巨头Facebook正积极探索并引领着一个被誉为“元宇宙”的全新领域,试图为用户打造更为真实、丰富的虚拟社交体验。 元宇宙的崛起 元宇宙这个概念…...

用React给XXL-JOB开发一个新皮肤(四):实现用户管理模块
目录 一. 简述二. 模块规划 2.1. 页面规划2.2. 模型实体定义 三. 模块实现 3.1. 用户分页搜索3.2. Modal 配置3.3. 创建用户表单3.4. 修改用户表单3.5. 删除 四. 结束语 一. 简述 上一篇文章我们实现登录页面和管理页面的 Layout 骨架,并对接登录和登出接口。这篇…...

某赛通电子文档安全管理系统 hiddenWatermark/uploadFile 文件上传漏洞复现
0x01 产品简介 某赛通电子文档安全管理系统(简称:CDG)是一款电子文档安全加密软件,该系统利用驱动层透明加密技术,通过对电子文档的加密保护,防止内部员工泄密和外部人员非法窃取企业核心重要数据资产,对电子文档进行全生命周期防护,系统具有透明加密、主动加密、智能…...

Redis五种数据类型及应用场景
1、数据类型 String(字符串,整数,浮点数):做简单的键值对缓存 List(列表):储存一些列表类型的数据结构 Hash(哈希):包含键值对的无序散列表,结构化的数据 Set(无序集合):交集,并集…...
测试环境搭建整套大数据系统(一:基础配置,修改hostname,hosts,免密)
一:使用服务器配置。 二:修改服务器名称hostname,hosts。 在 Linux 系统中,hostname 和 /etc/hosts 文件分别用于管理主机名和主机名解析。 在三台服务器上,分别执行以下命令。 vim /etc/hostnamexdso-hadoop-test-0…...
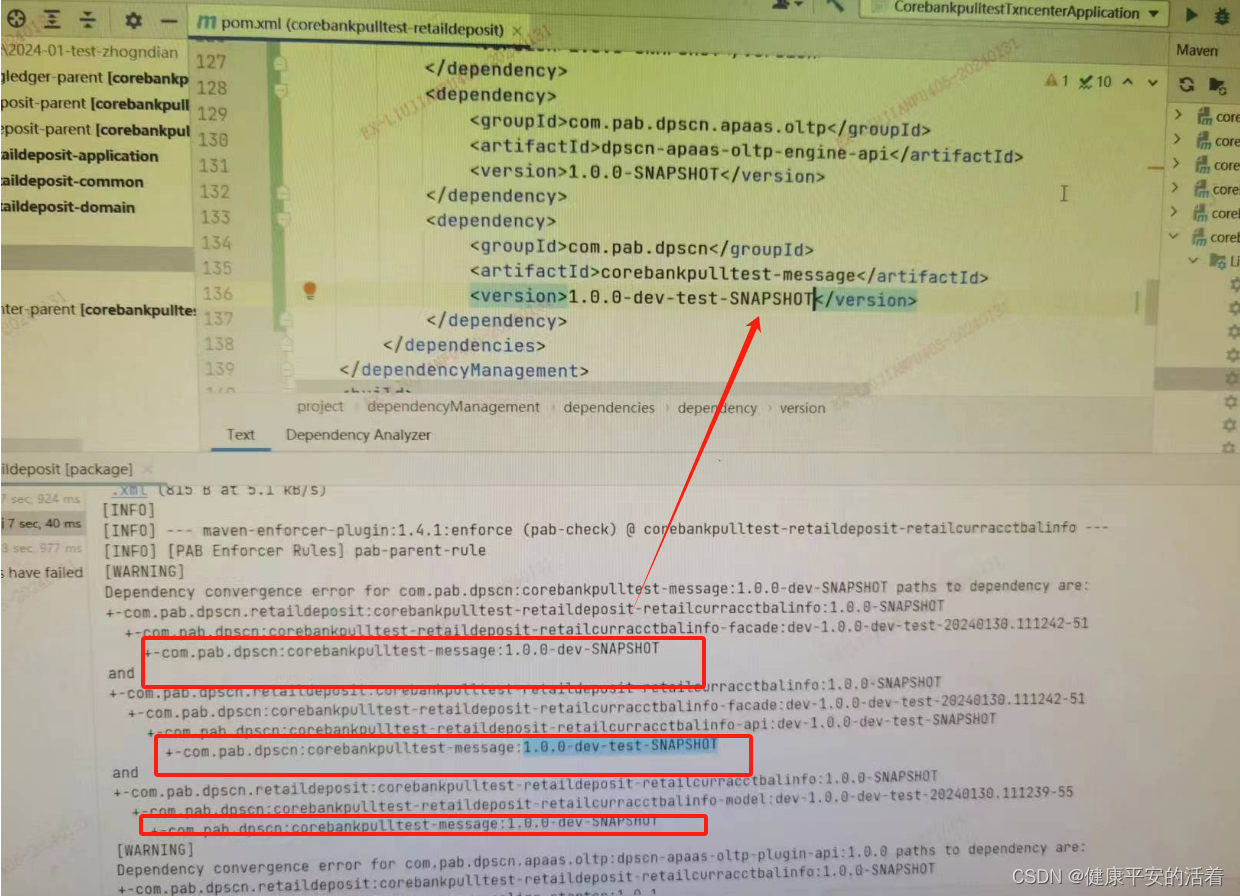
maven helper 解决jar包冲突方法
一 概要说明 1.1 说明 首先,解决idea中jar包冲突,使用maven的插件:maven helper插件,它能够给我们罗列出来同一个jar包的不同版本,以及他们的来源,但是对不同jar包中同名的类没有办法。 1.2 依赖顺序 …...
)
AppSrv-文件共享(23国赛真题)
2023全国职业院校技能大赛网络系统管理赛项–模块B:服务部署(WindowServer2022) 文章目录 AppSrv-文件共享题目配置步骤创建用户主目录共享文件夹:本地目录为d:\share\users\,允许所有域用户可读可写。在本目录下为所有用户添加一个以名称命名的文件夹,该文件夹将设置为所…...

AsyncLocal是如何实现在Thread直接传值的?
一:背景 1. 讲故事 这个问题的由来是在.NET高级调试训练营第十期分享ThreadStatic底层玩法的时候,有朋友提出了AsyncLocal是如何实现的,虽然做了口头上的表述,但总还是会不具体,所以觉得有必要用文字图表的方式来系统…...
Flask 入门1:一个简单的 Web 程序
1. 关于 Flask Flask诞生于2010年, Armin Ronacher的一个愚人节玩笑。不过现在已经是一个用python语言基于Werkzeug工具箱编写的轻量级web开发框架,它主要面向需求简单,项目周期短的小应用。 Flask本身相当于一个内核,其他几乎所…...
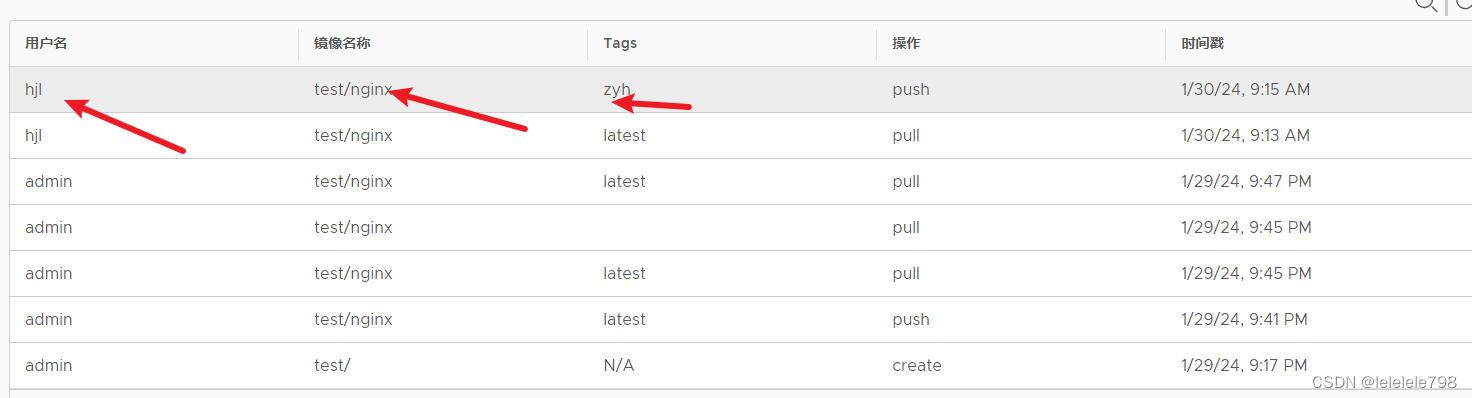
维护管理Harbor,docker容器的重启策略
维护管理Harbor 通过HarborWeb创建项目 在 Harbor 仓库中,任何镜像在被 push 到 regsitry 之前都必须有一个自己所属的项目。 单击“项目”,填写项目名称,项目级别若设置为"私有",则不勾选。如果设置为公共仓库&#…...
Qt6入门教程 14:QToolButton
目录 一.简介 二.常用接口 1.void setMenu(QMenu * menu) 2.void setPopupMode(ToolButtonPopupMode mode) 3.void setToolButtonStyle(Qt::ToolButtonStyle style) 4.void setArrowType(Qt::ArrowType type) 5.void setDefaultAction(QAction * action) 三.实战演练 1…...
3D数据转换器HOOPS Exchange如何获取模型的几何数据? 干货预警!
一、概述 前面讲解过模型在内存中的结构,现在回顾一下,当模型导入成功后,整个模型数据会以原生结构的 PRC 组装树形式存放到内存中。(申请 HOOPS Exchange 试用) PRC结构的主要类型包含四种,分别是…...

Coremail启动鸿蒙原生应用开发,打造全场景邮件办公新体验
1月18日,华为在深圳举行鸿蒙生态千帆启航仪式,Coremail出席仪式并与华为签署鸿蒙合作协议,宣布正式启动鸿蒙原生应用开发。作为首批拥抱鸿蒙的邮件领域伙伴,Coremail的加入标志着鸿蒙生态版图进一步完善。 Coremail是国内自建邮件…...

基于CVITEK_CV1821+SOI_Q03P的IPC方案
方案概述: 该方案基于主控平台CVITEK_CV1821和sensor SOI_Q03P,运用于智能监控IP摄像头,可用于户外或室内。采用了2304x1296的分辨率,30的帧率,支持HDR。作为3M的监控摄像头,通过ISP图像调校技术ÿ…...

chromedriver安装和环境变量配置
chromedriver 1、安装2、【重点】环境变量配置(1)包的复制:(2)系统环境变量配置 3、验证 1、安装 网上随便搜一篇chromedriver的安装文档即可。这里是一个快速链接 特别提醒:截止2024.1.30,chr…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
