###C语言程序设计-----C语言学习(8)## 斐波那契数列问题,素数问题,人数分配问题。
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。

今天,我们主要分享三个问题如何用C语言去求解,1.斐波那契数列问题,2.素数列举问题,3.人数分配问题。
一. 斐波那契数列问题
(1)问题叙述:斐波那契数列问题。输人正整数 n(1<=n<=46),输出斐波那契(Fibonacci)数列的前n项:1,1,2,3,5,8,13,·····,每行输出 5个。Fibonacci 数列就是满足任一项数字是前两项的和(最开始两项均定义为 1)的数列。
(2)问题分析:计算斐波那契数列时,从第 3 项开始,每一项的值就是前 2项的和。用两个变量存储最近产生的两个序列值,计算出新一项数据后,需要更新这两个变量的值。假定最开始两项分别用x1=1和x2=1表示,则新项x=x1+x2,然后更新x1和x2:x1=x2及x2=x,为计算下一个新项x作准备。题目要求输出n项,循环次数确定,可采用 for 语句。
(3)方法总结:迭代法也称辗转法,是一个不断从变量的旧值递推新值的过程,跟迭代法相对应的是直接法(或者称为一次解法),即一次性解决问题。迭代法是用计算机解决问题的一种基本方法,它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出新值。
(4)源程序:
#include <stdio.h>
int main()
{int i, n, x, x1, x2; //x1和x2依次代表前两项,x表示其后一项 printf("Enter n:"); //提示输入所需输出项的个数 scanf("%d", &n);if (n<1||n>46){printf("Invalid.\n");}else if (n==1){printf("%10d", 1); //n为1时输出1 }else{x1=1;x2=1;printf("%10d%10d", x1, x2); //先输出前两项 for (i=3; i<=n; i++) //循环输出n-2项 {x=x1+x2; //计算新的一项 printf("%10d", x);if (i%5==0){printf("\n"); //项数为5的倍数就换行 }//重新定义前两项 x1=x2; x2=x;}}return 0;}
二. 素数问题
(1)问题叙述:素数问题。输人2个正整数 m和n(1<=m<=n<=500),输出m到n之间的全部素数,每行输出 10个。素数就是只能被 1 和自身整除的正整数,1 不是素数,2 是素数。
(2)问题分析:可参照之前发的博客(如何判断素数)。
(3)源程序:
#include <stdio.h>
#include <math.h>
int main()
{int count, i, k, flag, limit, m, n; //flag表示是否为素数 printf("Enter m n:");scanf("%d %d", &m, &n);count=0; //count记录素数的个数 if (m<1||n>500||m>n){printf("Invalid.\n");}else {for (k=m; k<=n; k++){if (k<=1){flag=0;}else if (k==2){flag=1;}else{flag=1;limit=sqrt(k)+1;for (i=2; i<=limit; i++){if (k%i==0){flag=0;break;}}}if (flag==1){printf("%6d", k);count++;if (count%10==0) //count为10的倍数就换行 {printf("\n");}}}}return 0;
}
三. 搬砖问题
(1)问题叙述:搬砖问题。某工地需要搬运砖块,已知男人一人搬 3 块,女人一人搬 2块,小孩两人搬1块。如果想用n人正好搬n块砖,问有哪些搬法。
(2)问题分析:用枚举的思路,枚举对象是男人、女人和小孩的人数,将其分别设为变量 men、women和 children,以总人数 men+women+children ==n 和搬砖总数 men *3+women *2+children/2==n为判定条件,变量的取值范围都是[0,n]。3 个变量在各自的取值范围内遍历,采用三重循环嵌套,找出所有满足条件的解。
(3)源程序:
#include <stdio.h>
int main()
{int children, cnt, men, n, women;printf("Enter n:");scanf("%d", &n);cnt=0;for (men=0; men<=n; men++){for (women=0; women<=n; women++){for (children=0; children<=n; children++){if((men+women+children==n)&&(men*3+women*2+children*0.5==n)){printf("men=%d, women=%d, children=%d\n", men, women, children);cnt++;}}}}if (cnt==0){printf("None!\n");}return 0;}
感谢老铁的浏览,希望老铁可以一键三连加个关注,您的支持和鼓励是我前进的动力,后续会分享更多学习编程的内容。

相关文章:

###C语言程序设计-----C语言学习(8)## 斐波那契数列问题,素数问题,人数分配问题。
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 今天,我们主要分享三个问题如何用C语言去求解,1.斐波…...
蓝桥杯 第 1 场 小白入门赛
目录 1.蘑菇炸弹 2.构造数字 3.小蓝的金牌梦 4.合并石子加强版 5.简单的LIS问题 6.期望次数 1.蘑菇炸弹 我们直接依照题目 在中间位置的数进行模拟即可 void solve(){cin>>n;vector<int> a(n1);for(int i1;i<n;i) cin>>a[i];int ans0;for(int i2;i…...

飞天使-linux操作的一些技巧与知识点5-expect与docker便捷命令
expect 主要使用场景不输入账户密码的多 yum install -y expect 则可以安装上 #!/usr/bin/expect -f set username “root” set password “123456” spawn /bin/bash send “cd /data/container/\r” expect "$ " # 等待命令提示符 send “git pull\r” expect…...

编曲学习:和声音程 调式体系 唱名法 调式调性
34届和声音程 调式体系 唱名法 调式调性https://app8epdhy0u9502.pc.xiaoe-tech.com/live_pc/l_65af994be4b064a8cb1c3a5f?course_idcourse_2XLKtQnQx9GrQHac7OPmHD9tqbv 34届独立音乐人编曲训练营https://app8epdhy0u9502.pc.xiaoe-tech.com/p/t_pc/course_pc_detail/camp_p…...

【大数据】Flink 架构(四):状态管理
《Flink 架构》系列(已完结),共包含以下 6 篇文章: Flink 架构(一):系统架构Flink 架构(二):数据传输Flink 架构(三):事件…...

执行rpm安装命令的时候抛出异常:rpmdb BDB0113 Thread/process
问题现象 错误:rpmdb: BDB0113 Thread/process 66126/140498505373504 failed: BDB1507 Thread died in Berkeley DB library 错误:db5 错误(-30973) 来自 dbenv->failchk:BDB0087 DB_RUNRECOVERY: Fatal error, run database recovery 错…...

Android 在WebView中加载H5传递图片
最近h5开发一个编译器,要在手机上显示,需要获取手机上的图片,使用webview不能直接到文件管理拿取,还需要对webview做处理,做个记录,方便以后使用; public ValueCallback<Uri[]> mUploadMe…...
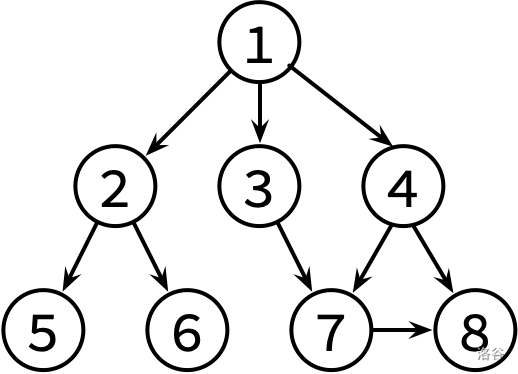
图的学习
图的基本概念和术语 图的定义:图是由顶点的有穷非空集合和顶点之间的边的集合组成的,G表示,V是图G中顶点的集合,E是图G中边的集合 无向图:任意两点的边都是无向边组成的图(无向边:(…...

空间数据分析入门POI与莫兰指数基础知识笔记
1. 空间分析与POI 1.1. 什么是POI POI是“Polnt of Information”的缩写,中文可以翻译为“信息点”。POI是地图上任何非地理意义的有意义的点,如商店、酒吧、加油站、医院、车站等。这些点通常包括名称、类别、经纬度和地址等基本信息。此外࿰…...
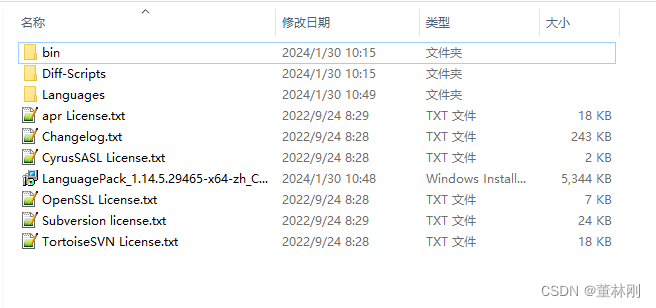
TortoiseSVN各版本汉化包下载
首先进入下载版本列表 1.下载地址:https://sourceforge.net/projects/tortoisesvn/files 2.选择自己版本进入 3.选择Language Packs进入,选择对应语言包下载。 4.在TortoiseSVN根目录下点击安装即可。 ...
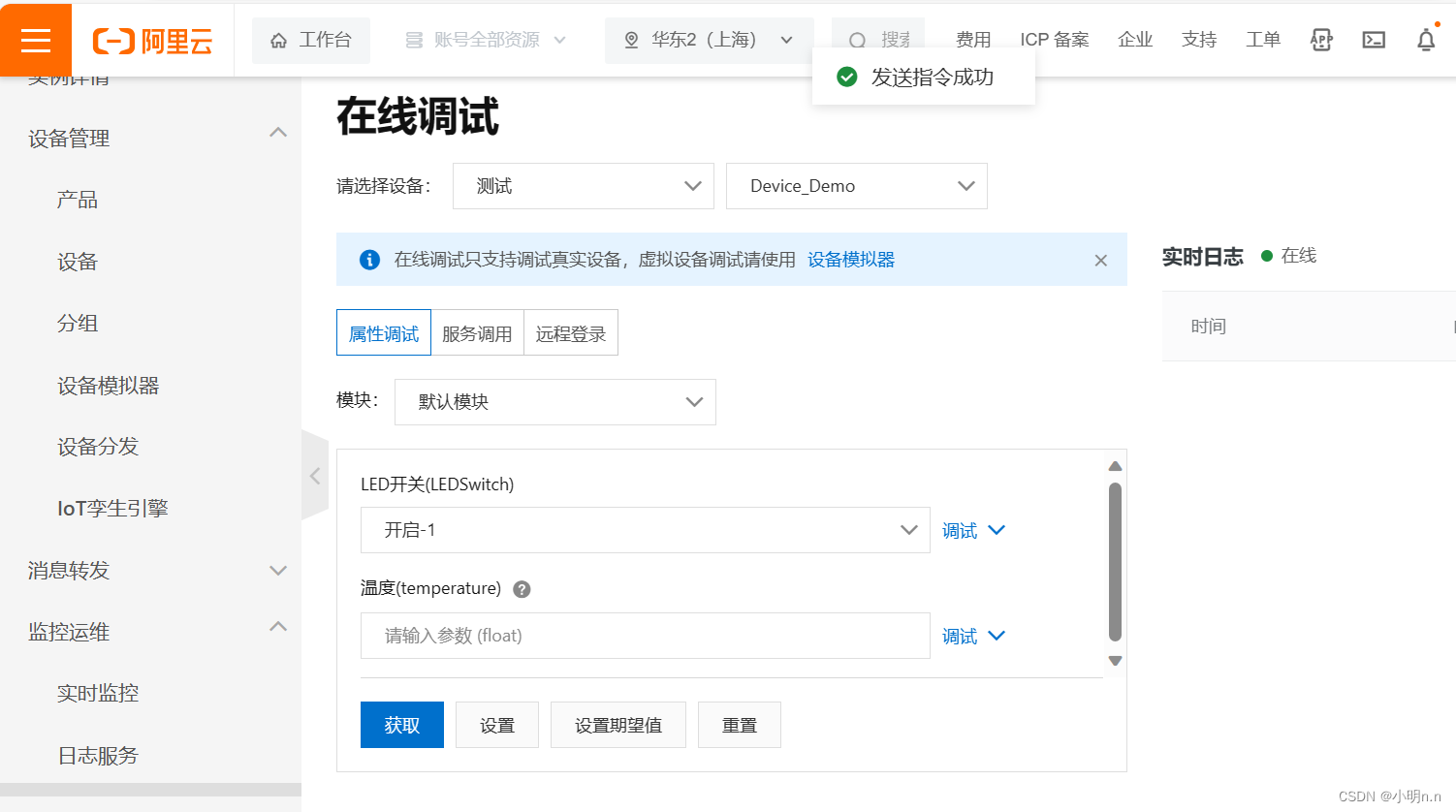
STM32连接阿里云物联网平台
文章目录 引言一、STM32连接阿里云物联网平台思路二、ESP8266烧录固件三、使用AT指令连接阿里云物联网平台四、STM32环形串口缓冲区驱动程序五、STM32连接阿里云驱动程序 引言 连续写了两篇关于阿里云连接的文章,都是使用Arduino ESP8266 & Arduino ESP32的方式…...
力扣hot100 组合总和 回溯 剪枝 组合
Problem: 39. 组合总和 文章目录 思路复杂度💖 Code 思路 复杂度 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( n ) O(n) O(n) 💖 Code class Solution{List<List<Integer>> res new ArrayList<>();int x;// 全局targetin…...
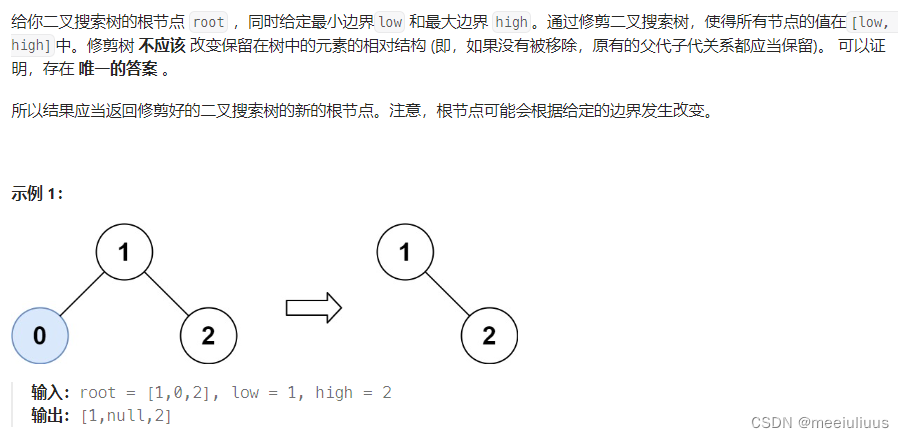
代码随想录 Leetcode669. 修剪二叉搜索树
题目: 代码(首刷看解析 2024年1月31日): class Solution { public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (!root) return root;if (root->val < low) {TreeNode* node trimBST(root->right,low,high);return…...
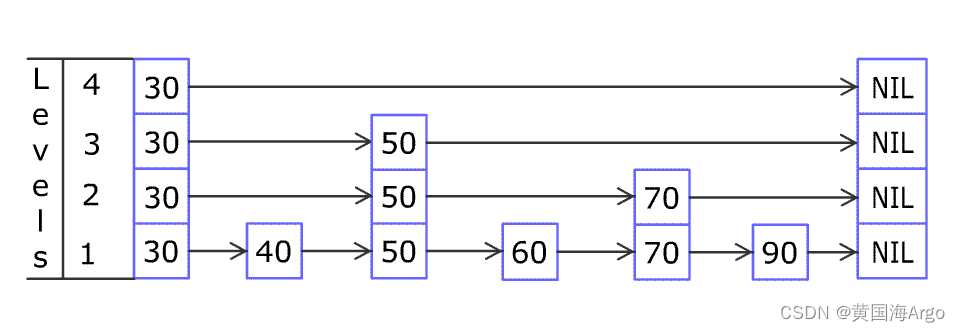
Redis系列-数据结构篇
数据结构 string(字符串) redis的字符串是动态字符串,类似于ArrayList,采用预分配冗余空间的方式减少内存的频繁分配。 struct SDS<T>{ T capacity; T len; byte flags; byte[] content; } 当字符串比较短时,…...
正则表达式(RE)
什么是正则表达式 正则表达式,又称规则表达式(Regular Expression)。正则表达式通常被用来检索、替换那些符合某个规则的文本 正则表达式的作用 验证数据的有效性替换文本内容从字符串中提取子字符串 匹配单个字符 字符功能.匹配任意1个…...

发布技术路线图!美国量子计算公司QuEra公开三年OKR
编辑丨慕一 编译/排版丨琳梦 卉可 深度好文:1100字丨8分钟阅读 近期,美国量子计算公司QuEra Computing宣布了一系列关于容错量子计算机的战略路线图,该路线图从2024年开始,最终目标是打造具有100纠错逻辑量子比特的系统。 在…...

Vue2:请求接口的两种方式axios和vue-resource
一、场景描述 前端和后端的交互,肯定是要发生接口调用的 这个时候,就要涉及前端如何向后端接口发送请求,获取数据 二、请求方式 1、axios方式(推荐) 这个方式本质就是ajax,底层就是对xhr(XMLHttpRequest)的封装 1、安装axios…...
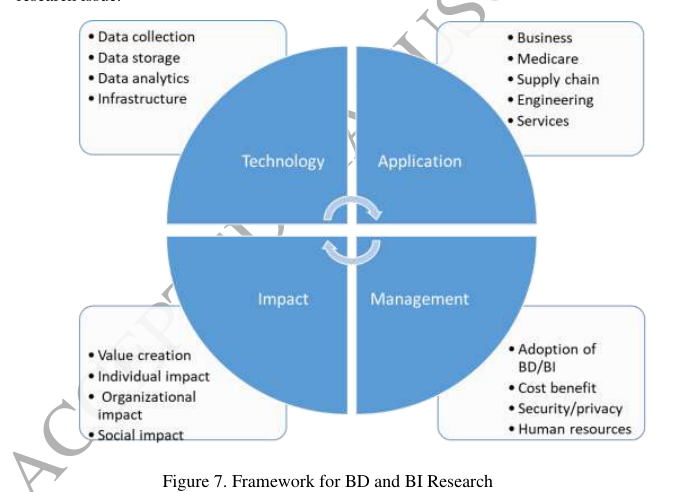
扩展学习|商业智能和大数据分析的研究前景(比对分析)
文献来源: Liang T P , Liu Y H .Research Landscape of Business Intelligence and Big Data analytics: A bibliometrics study[J].Expert Systems with Applications, 2018, 111(NOV.):2-10.DOI:10.1016/j.eswa.2018.05.018. 信息和通信技术的快速发展导致了数字…...

『Docker入门指南』- 详细安装与配置教程,助你起航容器化世界!
引言 在探索云计算和自动化部署的时代,Docker以其独特的容器化技术站在了风口浪尖。如果你期待着无缝地将你的应用从一个环境迁移到另一个环境,那么Docker无疑是你的得力助手。但首先,我们得学会如何正确地安装和配置Docker。这篇文章将详细…...

如何提高http连接成功率?
问题 丢包、错包、乱包 高延迟 响应数据回来时间长,甚至大于客户端等待时间 带宽小 每次能够通信的内容较少,数据包越大受影响可能越大 网络断续 网络经常断开又连接 优化处理 采用TCP协议、实现长连接,采用长连接池,节省…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
