瑞_力扣LeetCode_二叉搜索树相关题
文章目录
- 说明
- 题目 450. 删除二叉搜索树中的节点
- 题解
- 递归实现
- 题目 701. 二叉搜索树中的插入操作
- 题解
- 递归实现
- 题目 700. 二叉搜索树中的搜索
- 题解
- 递归实现
- 题目 98. 验证二叉搜索树
- 题解
- 中序遍历非递归实现
- 中序遍历递归实现
- 上下限递归
- 题目 938. 二叉搜索树的范围和
- 题解
- 中序遍历非递归实现
- 中序遍历递归实现
- 上下限递归实现
- 题目 1008. 前序遍历构造二叉搜索树
- 题解
- 直接插入
- 上限法
- 分治法
- 题目 235. 二叉搜索树的最近公共祖先
- 题解
🙊 前言:本文章为瑞_系列专栏之《刷题》的力扣LeetCode系列,主要以力扣LeetCode网的题进行解析与分享。本文仅供大家交流、学习及研究使用,禁止用于商业用途,违者必究!

说明
本文主要是配合《瑞_数据结构与算法_二叉搜索树》对二叉搜索树的知识进行提升和拓展,力扣中的树节点 TreeNode 相当于《瑞_数据结构与算法_二叉搜索树》中的 BSTNode,区别在于:
- TreeNode(力扣)属性有:val, left, right,并未区分键值
- BSTNode 属性有:key, value, left, right,区分了键值
TreeNode类(力扣):
/*** 力扣用到的二叉搜索树节点*/
class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val = val;}public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}@Overridepublic String toString() {return String.valueOf(val);}
}BSTNode类:
/*** 二叉搜索树, 泛型 key 版本*/
public class BSTTree2<K extends Comparable<K>, V> {static class BSTNode<K, V> {// 索引(泛型),比较值K key;// 该节点的存储值(泛型)V value;// 左孩子BSTNode<K, V> left;// 右孩子BSTNode<K, V> right;public BSTNode(K key) {this.key = key;}public BSTNode(K key, V value) {this.key = key;this.value = value;}public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {this.key = key;this.value = value;this.left = left;this.right = right;}}// 根节点BSTNode<K, V> root;
}所以力扣的 TreeNode 没有 key,比较二叉树节点用的是 TreeNode.val 属性与待删除 key 进行比较,因为力扣主要是练习题,对实际情况进行了简化
题目 450. 删除二叉搜索树中的节点
原题链接:450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
1️⃣首先找到需要删除的节点;
2️⃣如果找到了,删除它。
示例1:

输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围[0, 104].
- -105 <= Node.val <= 105
- 节点值唯一
root是合法的二叉搜索树- -105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
题解
删除remove(int key)方法需要考虑的情况较多。要删除某节点(称为 D),必须先找到被删除节点的父节点,这里称为 Parent,具体情况如下:
- 删除节点没有左孩子,将右孩子托孤给 Parent
- 删除节点没有右孩子,将左孩子托孤给 Parent
- 删除节点左右孩子都没有,已经被涵盖在情况1、情况2 当中,把 null 托孤给 Parent
- 删除节点左右孩子都有,可以将它的后继节点(称为 S)托孤给 Parent,设 S 的父亲为 SP,又分两种情况
- SP 就是被删除节点,此时 D 与 S 紧邻,只需将 S 托孤给 Parent
- SP 不是被删除节点,此时 D 与 S 不相邻,此时需要将 S 的后代托孤给 SP,再将 S 托孤给 Parent
删除本身很简单,只要通过索引查找到该节点删除即可,但是,由于需要料理后事,所以想要做好删除操作,需要处理好“托孤”操作。
递归实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode deleteNode(TreeNode node, int key) {if (node == null) {return null;}if (key < node.val) { // 没找到,继续递归调用node.left = deleteNode(node.left, key);return node;}if (node.val < key) { // 没找到,继续递归调用node.right = deleteNode(node.right, key);return node;}if (node.left == null) { // 情况1 - 只有右孩子return node.right;}if (node.right == null) { // 情况2 - 只有左孩子return node.left;}TreeNode s = node.right; // 情况3 - 有两个孩子while (s.left != null) {s = s.left;}s.right = deleteNode(node.right, s.val);s.left = node.left;return s;}
}
题目 701. 二叉搜索树中的插入操作
原题链接:701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例1:

输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:

示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在 [0, 104]的范围内。
- -108 <= Node.val <= 108
- 所有值
Node.val是 独一无二 的。 - -108 <= val <= 108
- 保证
val在原始BST中不存在。
题解
分为两种情况:
1️⃣ key在整个树中已经存在,新增操作变为更新操作,将旧的值替换为新的值
2️⃣ key在整个树中未存在,执行新增操作,将key value添加到树中
由于题目中的前提是:保证 val 在原始BST中不存在。因此只需考虑新增情况,不会出现更新情况
递归实现
- 若找到 key,走 else 更新找到节点的值
- 若没找到 key,走第一个 if,创建并返回新节点
- 返回的新节点,作为上次递归时 node 的左孩子或右孩子
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode insertIntoBST(TreeNode node, int val) {if (node == null) {return new TreeNode(val);}if (val < node.val) {node.left = insertIntoBST(node.left, val);} else if (node.val < val) {node.right = insertIntoBST(node.right, val);}return node;}
}
此处return node返回当前节点会多出一些额外的赋值动作。如下面这颗二叉搜索树,1作为插入节点,1和2通过node.left = insertIntoBST(node.left, val);建立父子关系返回,这是有必要的,但是由于递归,2和5也会通过node.left = insertIntoBST(node.left, val);建立父子关系,这样就是没必要的(因为5和2原本就存在父子关系),如果树的深度很大,那就会浪费很多性能。
5/ \2 6\ \1 3 7
题目 700. 二叉搜索树中的搜索
原题链接:700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点root和一个整数值val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例1:

输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
示例2:

输入:root = [4,2,7,1,3], val = 5
输出:[]
提示:
- 树中节点数在
[1, 5000]范围内 - 1 <= Node.val <= 107
root是二叉搜索树- 1 <= val <= 107
题解
递归实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode searchBST(TreeNode node, int val) {if (node == null) {return null;}if (val < node.val) {return searchBST(node.left, val);} else if (node.val < val) {return searchBST(node.right, val);} else {return node;}}
}
题目 98. 验证二叉搜索树
原题链接:98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在[1, 104] 内
- -231 <= Node.val <= 231 - 1
题解
合法的二叉搜索树即左边的都更小,右边的都更大,如下,第一个的树为合法二叉搜索树,而第二、三(等于也是非法的)均不合法
4 5 1/ \ / \ \2 6 4 6 1/ \ / \ 1 3 3 7
思路:利用二叉树中序遍历的特性(遍历后是升序的结果),所以遍历的结果一定是一个由小到大的结果,以此判断是否合法
瑞:关于二叉树中序遍历,可以参考《瑞_数据结构与算法_二叉树》
中序遍历非递归实现
public boolean isValidBST(TreeNode root) {TreeNode p = root;LinkedList<TreeNode> stack = new LinkedList<>();// 代表上一个值long prev = Long.MIN_VALUE;while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;} else {TreeNode pop = stack.pop();// 处理值,上一个值大于等于当前值的时候是非法二叉搜索树if (prev >= pop.val) {return false;}// 更新值prev = pop.val;p = pop.right;}}return true;
}
记录 prev 需要用 long,否则若测试用例中最小的节点为 Integer.MIN_VALUE 则测试会失败
中序遍历递归实现
使用递归的时候为避免性能浪费,可以进行剪枝操作。要注意在递归的时候不能用 Long 或 long,因为它们都是局部变量且不可变,因此每次赋值时,并不会改变其它方法调用时的 prev,所以要把 prev 设置为全局变量
// 全局变量记录 prevlong prev = Long.MIN_VALUE;public boolean isValidBST(TreeNode node) {if (node == null) {return true;}boolean a = isValidBST(node.left);// 剪枝if (!a) {return false;}// 处理值if (prev >= node.val) {return false;}prev = node.val;return isValidBST(node.right);}
瑞:以上代码在力扣中运行的时间是0ms,竟然优于中序遍历非递归实现的1ms,这里理论上说不过去,毕竟递归应该更耗费性能,但有可能由于力扣对栈的使用有自己的判定方式,所以可能造成这样的运行结果,但是理论上应该是非递归效率更好
上下限递归
可以对每个节点增加上下限,使用上限下限来递归判断。
- 根节点的下限是
-∞,上限是+∞ - 根节点的左孩子的下限是
-∞,上限是根节点值 - 根节点的右孩子的下限是根节点值,上限是上限是
+∞ - 以此递归
public boolean isValidBST(TreeNode node) {return doValid(node, Long.MIN_VALUE, Long.MAX_VALUE);
}private boolean doValid(TreeNode node, long min, long max) {if (node == null) {return true;}if (node.val <= min || node.val >= max) {return false;}return doValid(node.left, min, node.val) && doValid(node.right, node.val, max);
}
- 设每个节点必须在一个范围内: ( m i n , m a x ) (min, max) (min,max),不包含边界,若节点值超过这个范围,则返回 false
- 对于 node.left 范围肯定是 ( m i n , n o d e . v a l ) (min, node.val) (min,node.val)
- 对于 node.right 范围肯定是 ( n o d e . v a l , m a x ) (node.val, max) (node.val,max)
- 一开始不知道 min,max 则取 java 中长整数的最小、最大值
- 本质是前序遍历 + 剪枝
题目 938. 二叉搜索树的范围和
原题链接:938. 二叉搜索树的范围和
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和。
示例 1:

输入:root = [10,5,15,3,7,null,18], low = 7, high = 15
输出:32
示例 2:

输入:root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出:23
提示:
- 树中节点数目在范围 [1, 2 * 104] 内
- 1 <= Node.val <= 105
- 1 <= low <= high <= 105
- 所有
Node.val互不相同
题解
中序遍历非递归实现
思路:使用中序遍历(升序)判断,如果在范围内就进行累加,最终返回和。使用中序遍历的特性,当遍历到累加区间上限的时候,遍历即可停止。
public int rangeSumBST(TreeNode node, int low, int high) {TreeNode p = node;LinkedList<TreeNode> stack = new LinkedList<>();int sum = 0;while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;} else {TreeNode pop = stack.pop();// 处理值if (pop.val > high) {// 提前结束遍历break;}if (pop.val >= low) {sum += pop.val;}p = pop.right;}}return sum;}
虽然此解法思路很好想到,但是放到力扣上跑就发现,需要耗时4ms,还有很大的优化空间,因为只筛选了上限而不能跳过下限。
中序遍历递归实现
将上个方案修改为递归实现,耗时减少
public int rangeSumBST(TreeNode node, int low, int high) {if (node == null) {return 0;}int a = rangeSumBST(node.left, low, high);int b = 0;if (node.val >= low && node.val <= high) {b = node.val;}return a + b + rangeSumBST(node.right, low, high);
}
虽然在力扣上提升到了1ms,但是仍然有更好的方式
上下限递归实现
思路:中序遍历的性能提升瓶颈在于上限无法被跳过,那就使用上下限递归的方案,当递归到上限的时候,其递归就可以结束,同理递归到下限的时候,其递归就可以结束。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int rangeSumBST(TreeNode node, int low, int high) {if (node == null) {return 0;}// 此分支只需考虑它右子树的累加结果if (node.val < low) {return rangeSumBST(node.right, low, high);}// 此分支只需考虑它左子树的累加结果if (node.val > high) {return rangeSumBST(node.left, low, high);}// node.val 在范围内,需要把当前节点的值加上其左右子树的累加结果return node.val +rangeSumBST(node.left, low, high) +rangeSumBST(node.right, low, high);}
}
在力扣上运行只耗时 0 ms
题目 1008. 前序遍历构造二叉搜索树
原题链接:1008. 前序遍历构造二叉搜索树
给定一个整数数组,它表示BST(即 二叉搜索树 )的 先序遍历 ,构造树并返回其根。
保证 对于给定的测试用例,总是有可能找到具有给定需求的二叉搜索树。
二叉搜索树 是一棵二叉树,其中每个节点, Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。
二叉树的 前序遍历 首先显示节点的值,然后遍历Node.left,最后遍历Node.right。
示例1:

输入:preorder = [8,5,1,7,10,12]
输出:[8,5,10,1,7,null,12]
示例2:
输入: preorder = [1,3]
输出: [1,null,3]
提示:
- 1 <= preorder.length <= 100
- 1 <= preorder[i] <= 108
- preorder 中的值 互不相同
题解
注意前提,前序遍历数组的长度是大于等于1的(肯定存在根节点),且数组中的值互不相同(只需考虑插入的情况而不需要考虑更新的情况)
直接插入
思路:根据前序遍历的结果,可以唯一地构造出一个二叉搜索树。所以可以从左向右,以此插入节点思想的思想构建二叉树。
如前序遍历结果为:[8,5,1,7,10,12]。那么8作为根节点,5比8(根节点)小,查看到8的左孩子为空,插入。继续遍历插入1,1比8(根节点)小,但是8的左子树已经有了5,1比5小,所以查看到5的左孩子为空,插入。继续遍历插入7,7比8(根节点)小,但是8的左子树已经有了5,7比5大,所以查看到8的右孩子为空,插入。继续遍历10,10比8(根节点)大,查看到8的右孩子为空,插入。继续遍历12,12比8(根节点)大,但是8的右子树已经有了10,12比10大,查看10的右孩子为空,插入。遍历结束,二叉搜索树构造完成,如下:
8/ \5 10/ \ \1 7 12
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode bstFromPreorder(int[] preorder) {TreeNode root = insert(null, preorder[0]);for (int i = 1; i < preorder.length; i++) {insert(root, preorder[i]);}return root;}private TreeNode insert(TreeNode node, int val) {if (node == null) {return new TreeNode(val);}if (val < node.val) {node.left = insert(node.left, val);} else if (node.val < val) {node.right = insert(node.right, val);}return node;}
}
虽然耗时为0ms,但是时间复杂度为 O(n long n),可以优化
上限法
思路:
1.遍历数组中每一个值,根据值创建节点
每个节点若成功创建则加上:左孩子上限,右孩子上限
2.处理下一个值时,如果超过此上限,那么
将 null 作为上个节点的孩子
不能创建节点对象
直到不超过上限位置
3.重复1.2.步骤
8/ \5 10/ \ \1 7 12
如上二叉搜索树的前序遍历结果为:[8,5,1,7,10,12]。
则根节点8左限为8,右限为MAX。
继续遍历5,5左限为5,右限为8。
继续遍历1,1左限为1,右限为5。
继续遍历7,7超过1的左限1,不能作为1的左孩子,所以此时设置1的左孩子为null,7超过1的右限5,所以7也不能作为1的右孩子,此时设置1的右孩子为null,此时1的左右孩子均为null,代表1结束,此时建立1和5的父子关系,继续判断,7没有超过5的右限8,所以7可以作为5的右孩子,所以7的左限为7右限位8。
继续遍历10,10超过7的左限7,不能作为7的左孩子,所以此时设置7的左孩子为null,10超过7的右限8,所以10也不能作为7的右孩子,此时设置7的右孩子为null,此时7的左右孩子均为null,代表7结束,此时建立7和5的父子关系,此时5有左孩子1,右孩子7,5节点构建完成,将10与5的上一个节点8继续判断,10超过8的左限8,10小于8的右限MAX,所以10可以作为8的右孩子,此时8的左孩子为5右孩子为10,8构建完成,10的左限为10,右限为MAX。
继续遍历12,12超过10的左限10,不能作为10的左孩子,此时设置10的左孩子为null,12没有超过10的右限MAX,所以10可以作为12的右孩子,此时10的左孩子为null右孩子为12,10构建完成,遍历此时也结束,二叉搜索树构建完成。
public TreeNode bstFromPreorder(int[] preorder) {return insert(preorder, Integer.MAX_VALUE);
}int i = 0;
private TreeNode insert(int[] preorder, int max) {if (i == preorder.length) {return null;}int val = preorder[i];
// System.out.println(val + String.format("[%d]", max));if (val > max) {return null;}TreeNode node = new TreeNode(val);i++;node.left = insert(preorder, node.val); node.right = insert(preorder, max); return node;
}
依次处理 prevorder 中每个值, 返回创建好的节点或 null 作为上个节点的孩子
- 如果超过上限, 返回 null
- 如果没超过上限, 创建节点, 并将其左右孩子设置完整后返回
- i++ 需要放在设置左右孩子之前,意思是从剩下的元素中挑选左右孩子
时间复杂度为 O(long n)
分治法
思想:利用前序遍历的特性(第一个元素为根节点,往后小于根节点的是左子树,大于根节点的是右子树,区分出根左右),通过递归的方式,不断拆解,缩小区域,直到区域内没有元素则划分完成。
8/ \5 10/ \ \1 7 12
如上二叉搜索树的前序遍历结果为:[8,5,1,7,10,12]
- 刚开始 8, 5, 1, 7, 10, 12,方法每次执行,确定本次的根节点和左右子树的分界线
- 第一次确定根节点为 8,左子树 5, 1, 7,右子树 10, 12
- 对 5, 1, 7 做递归操作,确定根节点是 5, 左子树是 1, 右子树是 7
- 对 1 做递归操作,确定根节点是 1,左右子树为 null
- 对 7 做递归操作,确定根节点是 7,左右子树为 null
- 对 10, 12 做递归操作,确定根节点是 10,左子树为 null,右子树为 12
- 对 12 做递归操作,确定根节点是 12,左右子树为 null
- 递归结束,返回本范围内的根节点
public TreeNode bstFromPreorder(int[] preorder) {return partition(preorder, 0, preorder.length - 1);
}private TreeNode partition(int[] preorder, int start, int end) {if (start > end) {return null;}TreeNode root = new TreeNode(preorder[start]);int index = start + 1;while (index <= end) {if (preorder[index] > preorder[start]) {break;}index++;}// index 就是右子树的起点root.left = partition(preorder, start + 1, index - 1);root.right = partition(preorder, index, end);return root;
}
时间复杂度为 O(n long n)
题目 235. 二叉搜索树的最近公共祖先
原题链接:235. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/description/
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

提示1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
提示2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
题解
思路:若 p,q 在 ancestor 的两侧(含p,q自身),则 ancestor 就是它们的最近公共祖先。
__ 6 __/ \2 8/ \ / \0 4 7 9/ \3 5
如上二叉搜索树:假设p为2,q为8,则6为它们的最近公共祖先。
再如4和5,都在6的左子树,属于一侧,所以6就不是它们公共祖先。继续往6的左子树下遍历2,4和5在2的右子树,也属于一侧,所以2不是它们的公共祖先。继续往2的右子树下遍历4,4等于4,5大于4,则可认为不在同一侧,即4和5在4的两侧,4为4和5的最近公共祖先。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {TreeNode ancestor = root;// 条件成立表示在同一侧while (ancestor.val > p.val && ancestor.val > q.val ||ancestor.val < p.val && ancestor.val < q.val) {if (ancestor.val > p.val) {ancestor = ancestor.left;} else {ancestor = ancestor.right;}}return ancestor;}
}
如果觉得这篇文章对您有所帮助的话,请动动小手点波关注💗,你的点赞👍收藏⭐️转发🔗评论📝都是对博主最好的支持~
相关文章:

瑞_力扣LeetCode_二叉搜索树相关题
文章目录 说明题目 450. 删除二叉搜索树中的节点题解递归实现 题目 701. 二叉搜索树中的插入操作题解递归实现 题目 700. 二叉搜索树中的搜索题解递归实现 题目 98. 验证二叉搜索树题解中序遍历非递归实现中序遍历递归实现上下限递归 题目 938. 二叉搜索树的范围和题解中序遍历…...

python爬虫爬取网站
流程: 1.指定url(获取网页的内容) 爬虫会向指定的URL发送HTTP请求,获取网页的HTML代码,然后解析HTML代码,提取出需要的信息,如文本、图片、链接等。爬虫请求URL的过程中,还可以设置请求头、请求参数、请求…...
c# Get方式调用WebAPI,WebService等接口
/// <summary> /// 利用WebRequest/WebResponse进行WebService调用的类 /// </summary> public class WebServiceHelper {//<webServices>// <protocols>// <add name"HttpGet"/>// <add name"HttpPost"/>// …...

银行数据仓库体系实践(11)--数据仓库开发管理系统及开发流程
数据仓库管理着整个银行或公司的数据,数据结构复杂,数据量庞大,任何一个数据字段的变化或错误都会引起数据错误,影响数据应用,同时业务的发展也带来系统不断升级,数据需求的不断增加,数据仓库需…...

微信小程序引导用户打开定位授权通用模版
在需要使用位置信息的页面(例如 onLoad 或 onShow 生命周期函数)中调用 wx.getSetting 方法检查用户是否已经授权地理位置权限: Page({onLoad: function() {wx.getSetting({success: res > {if (res.authSetting[scope.userLocation]) {/…...

JVM篇----第十篇
系列文章目录 文章目录 系列文章目录前言一、JAVA 强引用二、JAVA软引用三、JAVA弱引用四、JAVA虚引用五、分代收集算法前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码吧…...
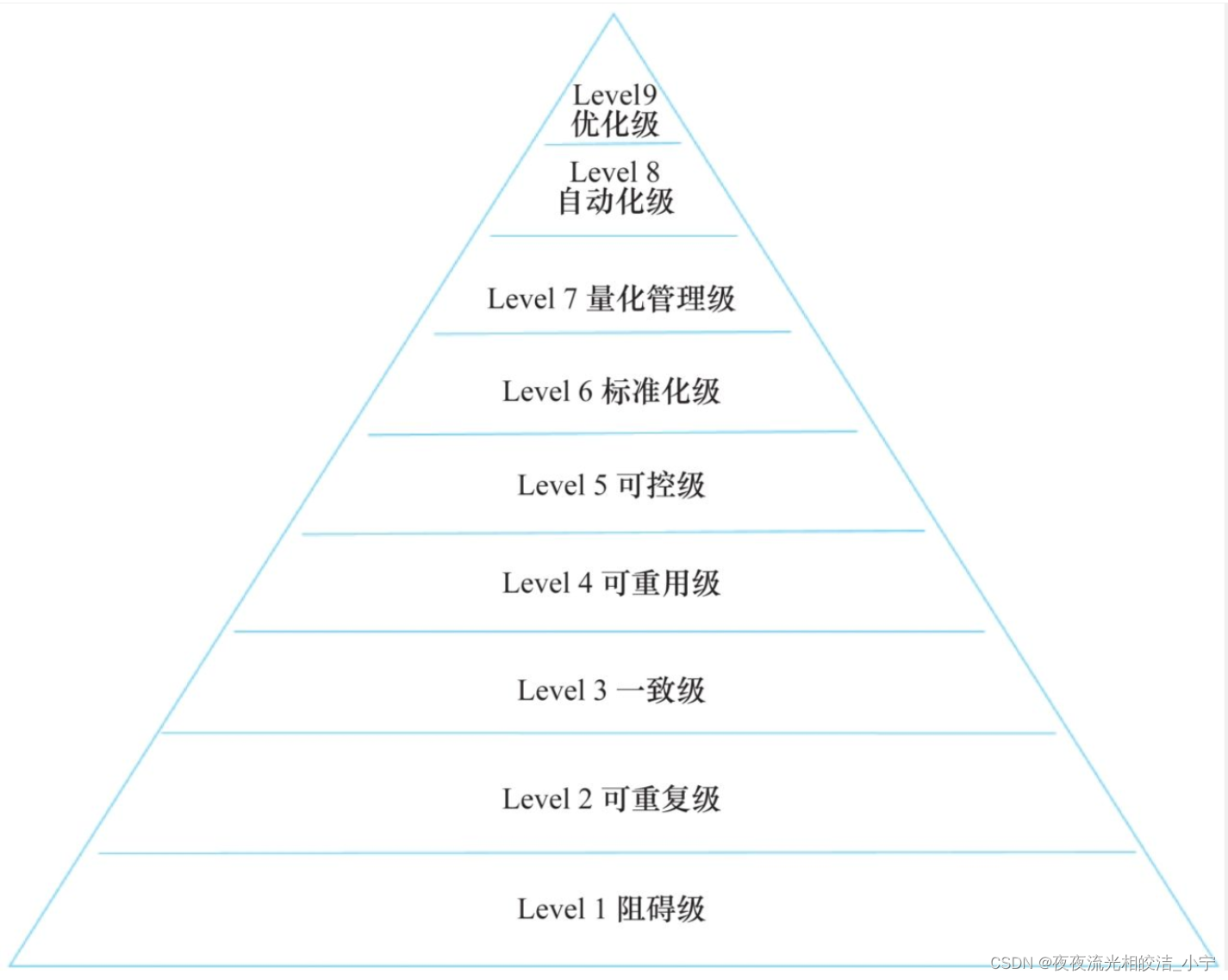
DevSecOps 参考模型介绍
目录 一、参考模型概述 1.1 概述 二、参考模型分类 2.1 DevOps 组织型模型 2.1.1 DevOps 关键特性 2.1.1.1 模型特性图 2.1.1.2 特性讲解 2.1.1.2.1 自动化 2.1.1.2.2 多边协作 2.1.1.2.3 持续集成 2.1.1.2.4 配置管理 2.1.2 DevOps 生命周期 2.1.2.1 研发过程划分…...

什么是okhttp?
OkHttp简介: OkHttp 是一个开源的、高效的 HTTP 客户端库,由 Square 公司开发和维护。它为 Android 和 Java 应用程序提供了简单、强大、灵活的 HTTP 请求和响应的处理方式。OkHttp 的设计目标是使网络请求变得更加简单、快速、高效,并且支持…...
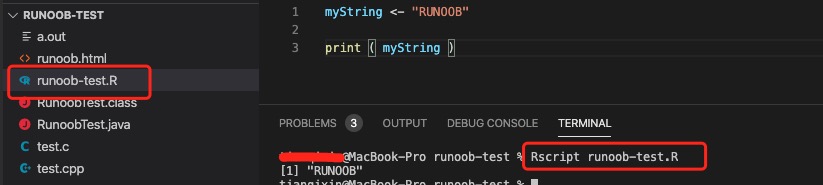
R语言基础学习-02 (此语言用途小众 用于数学 生物领域 基因分析)
变量 R 语言的有效的变量名称由字母,数字以及点号 . 或下划线 _ 组成。 变量名称以字母或点开头。 变量名是否正确原因var_name2.正确字符开头,并由字母、数字、下划线和点号组成var_name%错误% 是非法字符2var_name错误不能数字开头 .var_name, var.…...
CTF-WEB的入门真题讲解
EzLogin 第一眼看到这个题目我想着用SQL注入 但是我们先看看具体的情况 我们随便输入admin和密码发现他提升密码不正确 我们查看源代码 发现有二个不一样的第一个是base64 意思I hava no sql 第二个可以看出来是16进制转化为weak通过发现是个弱口令 canyouaccess 如果…...
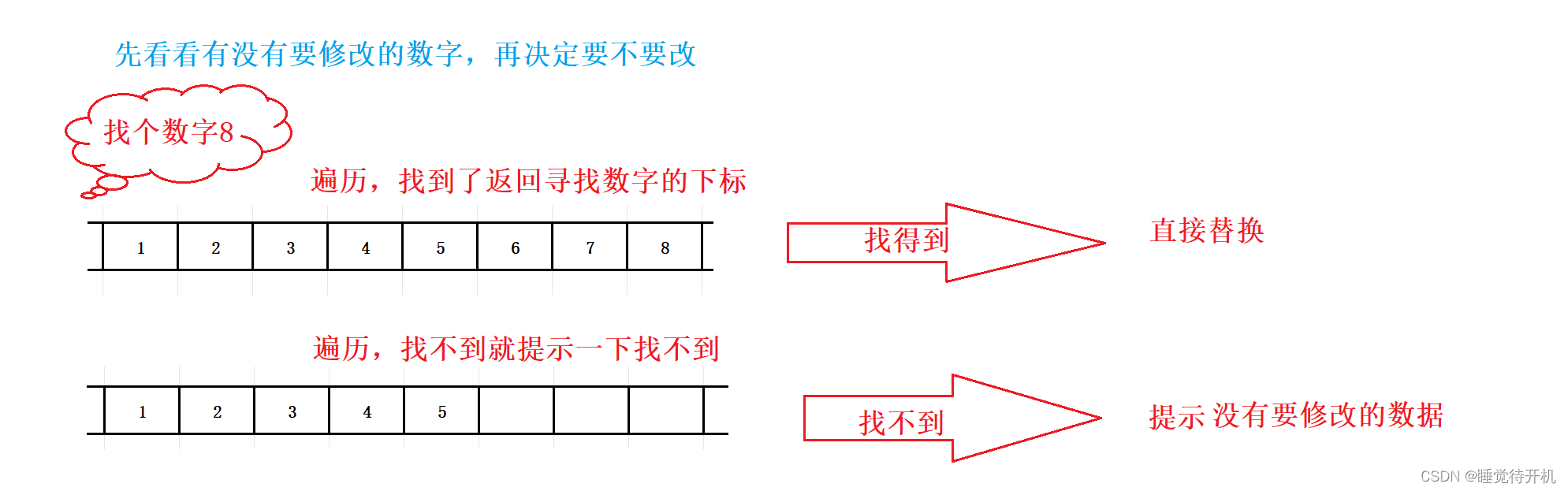
【C项目】顺序表
简介:本系列博客为C项目系列内容,通过代码来具体实现某个经典简单项目 适宜人群:已大体了解C语法同学 作者留言:本博客相关内容如需转载请注明出处,本人学疏才浅,难免存在些许错误,望留言指正 作…...
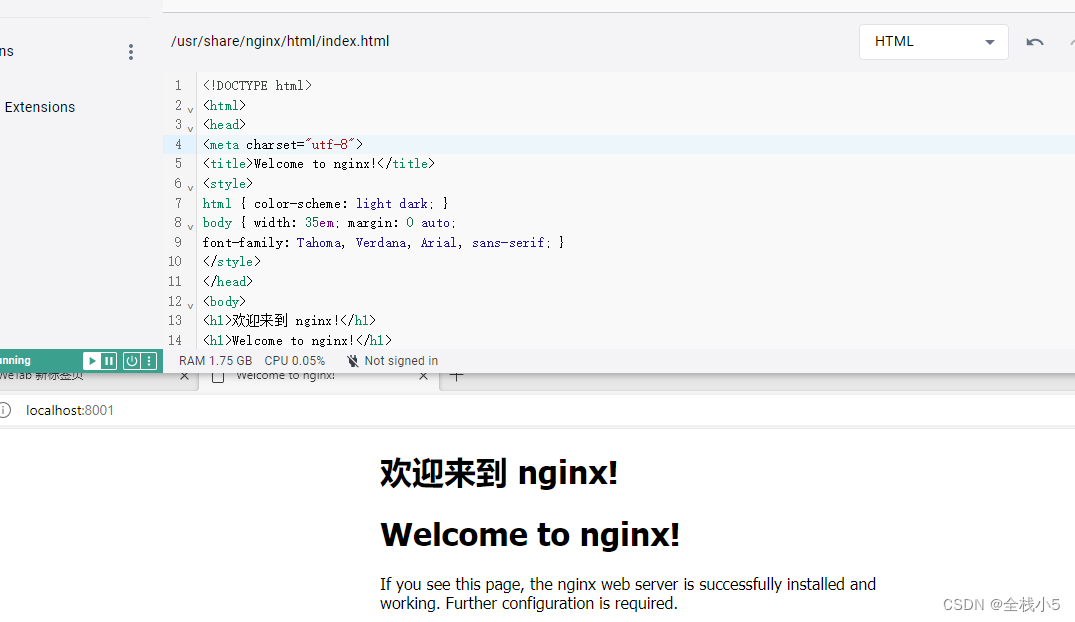
【Docker】在Windows下使用Docker Desktop创建nginx容器并访问默认网站
欢迎来到《小5讲堂》,大家好,我是全栈小5。 这是《Docker容器》序列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对…...

详讲api网关之kong的基本概念及安装和使用(二)
consul的服务注册与发现 如果不知道consul的使用,可以点击上方链接,这是我写的关于consul的一篇文档。 upstreamconsul实现负载均衡 我们知道,配置upstream可以实现负载均衡,而consul实现了服务注册与发现,那么接下来…...
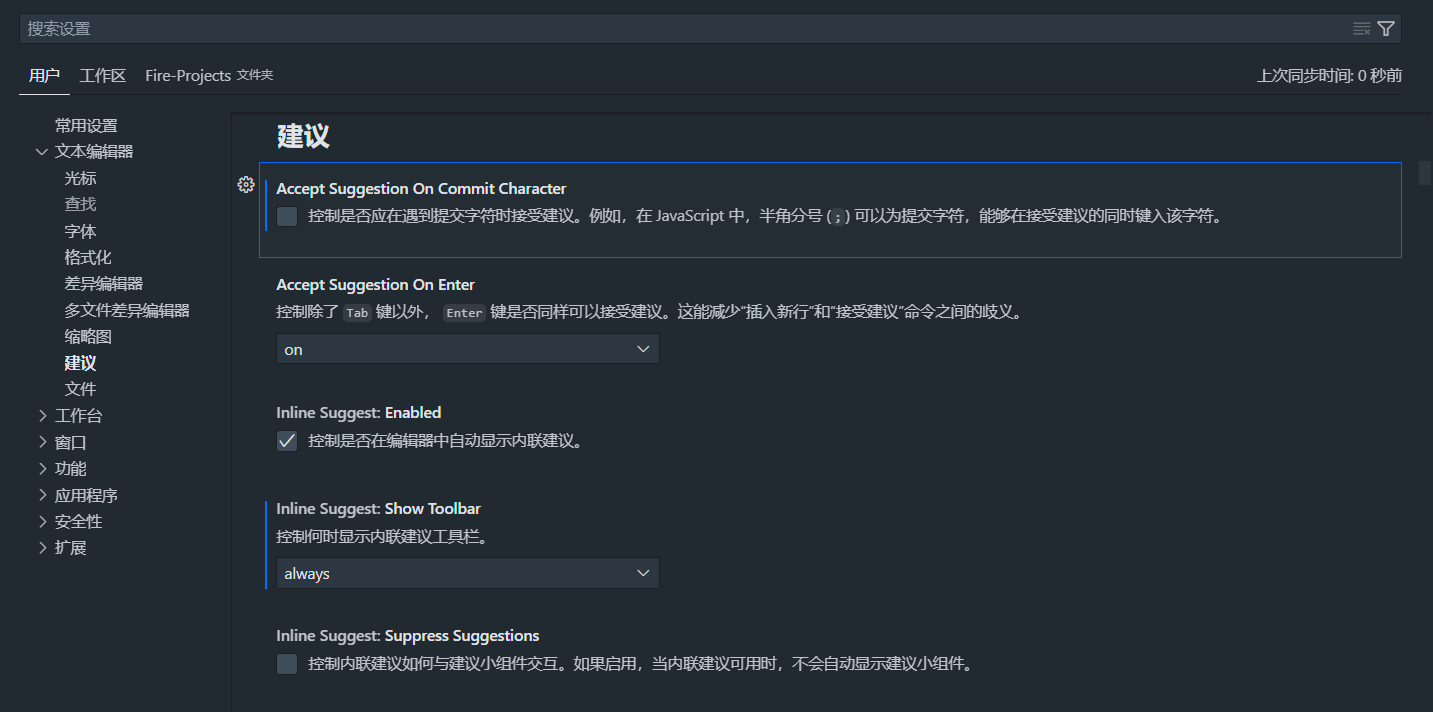
取消Vscode在输入符号时自动补全
取消Vscode在输入符号时自动补全 取消Vscode在输入符号时自动补全问题演示解决方法 取消Vscode在输入符号时自动补全 问题演示 在此状态下输入/会直接自动补全, 如下图 笔者想要达到的效果为可以正常输入/而不进行补全, 如下图 解决方法 在设置->文本编辑器->建议, 取消…...

ElementUI Form:Input 输入框
ElementUI安装与使用指南 Input 输入框 点击下载learnelementuispringboot项目源码 效果图 el-input.vue 页面效果图 项目里el-input.vue代码 <script> export default {name: el_input,data() {return {input: ,input1: ,input2: ,input3: ,input4: ,textarea: …...

Vue_Router_守卫
路由守卫:路由进行权限控制。 分为:全局守卫,独享守卫,组件内守卫。 全局守卫 //创建并暴露 路由器 const routernew Vrouter({mode:"hash"//"hash路径出现#但是兼容性强,history没有#兼容性差"…...

GDB调试技巧实战--自动化画出类关系图
1. 前言 上节我们在帖子《Modern C++利用工具快速理解std::tuple的实现原理》根据GDB的ptype命令快速的理解了std::tuple数据结构的实现,但是手动一个个打印,然后手动画出的UML图,这个过程明显可以自动化。 本文旨在写一个GDB python脚本把这个过程自动化。 本脚本也可以用…...

python使用Schedule
目录 一:使用场景: 二:参数 三:实例 "Schedule"在Python中通常指的是时间调度或任务计划。Python中有多个库可以用来处理时间调度和任务计划,其中最流行的是schedule库。 一&#x…...
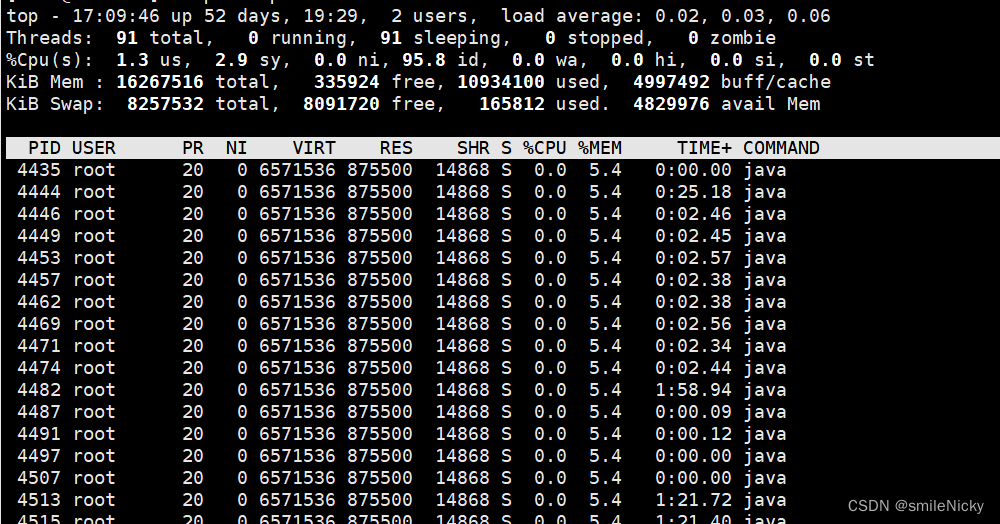
Linux系列之查看cpu、内存、磁盘使用情况
查看磁盘空间 df命令用于显示磁盘分区上的可使用的磁盘空间。默认显示单位为KB。可以利用该命令来获取硬盘被占用了多少空间,目前还剩下多少空间等信息。使用df -h命令,加个-h参数是为了显示GB MB KB单位,这样更容易查看 Filesystem …...

【C语言】socket编程接收问题
一、recv()函数接收到的返回值为0表示对端已经关闭 在TCP套接字编程中,通过recv()函数接收到的返回值为0通常表示对端已经关闭了套接字的发送部分。这是因为TCP是一个基于连接的协议,其中有定义明确的连接建立和终止流程;当对端调用close()或…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
