C++ 数论相关题目:高斯消元解异或线性方程组
输入一个包含 n
个方程 n
个未知数的异或线性方程组。
方程组中的系数和常数为 0
或 1
,每个未知数的取值也为 0
或 1
。
求解这个方程组。
异或线性方程组示例如下:
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中 ^ 表示异或(XOR
),M[i][j]
表示第 i
个式子中 x[j]
的系数,B[i]
是第 i
个方程右端的常数,取值均为 0
或 1
。
输入格式
第一行包含整数 n
。
接下来 n
行,每行包含 n+1
个整数 0
或 1
,表示一个方程的 n
个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n
行,其中第 i
行输出第 i
个未知数的解。
如果给定线性方程组存在多组解,则输出 Multiple sets of solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100
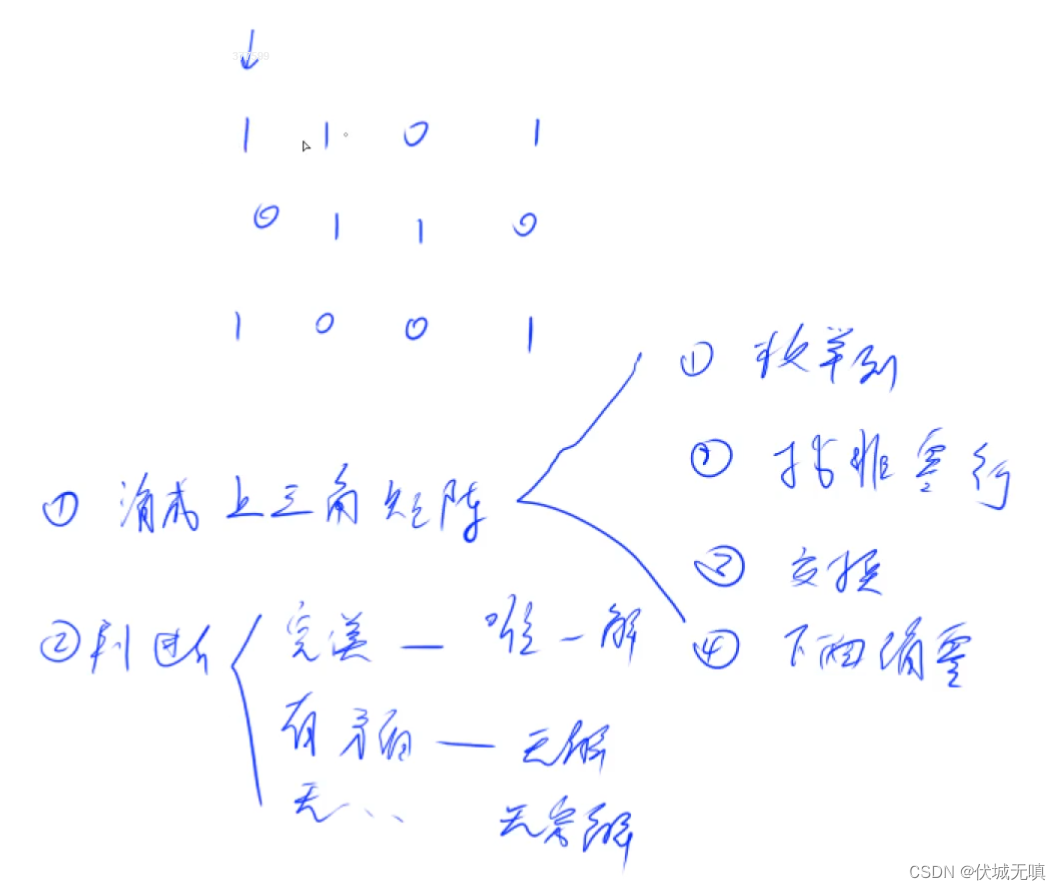
输入样例:
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例:
1
0
0
#include <iostream>
#include <algorithm>using namespace std;const int N = 110;int n;
int a[N][N];int xor_gauss()
{int c, r;for(c = 0, r = 0; c < n; c ++ ){int t = r;for(int i = r; i < n; i ++ )if(a[i][c]) //找到第一个非零行就行{t = i;break;}if(!a[t][c]) //往下找完发现并不存在一个非零的,这列就结束了continue;for(int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);for(int i = r + 1; i < n; i ++ )if(a[i][c]) //如果不为0,才消去for(int j = n; j >= c; j -- )a[i][j] = a[i][j] ^ a[r][j];r ++; }if(r < n){for(int i = r; i < n; i ++ ) //判断是否有矛盾,现在i行左边是全部为0的,右边不为0,出现矛盾if(a[i][n])return 0; //无解return 2; // 无穷组解}for(int i = n - 1; i >= 0; i -- ) //回带求解for(int j = i + 1; j < n; j ++ )a[i][n] = a[i][n] ^ a[i][j] & a[j][n]; //a[j][n] 此时就是xj的值return 1; //唯一解
}int main ()
{cin>>n;for(int i = 0; i < n; i ++ )for(int j = 0; j <= n; j ++ )cin>>a[i][j];int res = xor_gauss();if(res == 1) for(int i = 0; i < n; i ++ )cout<<a[i][n]<<endl;else if(res == 2)cout<<"Multiple sets of solutions"<<endl;elsecout<<"No solution"<<endl;return 0;}
相关文章:

C++ 数论相关题目:高斯消元解异或线性方程组
输入一个包含 n 个方程 n 个未知数的异或线性方程组。 方程组中的系数和常数为 0 或 1 ,每个未知数的取值也为 0 或 1 。 求解这个方程组。 异或线性方程组示例如下: M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] B[1] M[2][1]x[1] ^ M[2][2]x[2]…...
嵌入式学习第十四天
1.结构体(2): (1)结构体类型定义 (2)结构体变量的定义 (3)结构体元素的访问 (4)结构体的存储: 内存对齐: char 按照1字节对齐 …...

氢气泄漏检测仪使用方法:守护安全,从细节开始
随着科技的发展,我们的生活和工作环境中充满了各种潜在的危险。其中,氢气作为一种清洁能源,其使用日益广泛,但同时也带来了泄漏的风险。为了确保我们的安全,了解并正确使用氢气泄漏检测仪至关重要。下面将详细介绍氢气…...
【前端web入门第二天】01 html语法实现列表与表格_合并单元格
html语法实现列表与表格 文章目录: 1.列表 1.1 无序列表1.2 有序列表1.3 定义列表 2.表格 2.1 表格基本结构2.2 表格结构标签2.3 合并单元格 写在最前,第二天学习目标: 列表 表格 表单 元素为嵌套关系 1.列表 作用:布局内容排列整齐的区域。 列表分类:无序列表、有序列表…...

推荐系统|排序_MMOE
MMOE MMOE是指Multi-gate Mixture-of-Experts 注意看Expert后面加了s,说明了有多个专家。 而在MMOE中专家是指用来对输入特征计算的神经网络,每个神经网络根据输入计算出来的向量都会有所不同。 MMOE的低层 MMOE的上一层 通过MMOE的低层算出的向量和权…...

Redis拒绝连接的原因与解决方式
Redis拒绝连接的原因与解决方式 在某些情况下,当尝试从外部计算机连接到运行在保护模式下的Redis服务器时,您可能会遇到如下的错误信息: Caused by: org.redisson.client.RedisException: DENIED Redis is running in protected mode becau…...

Neo4j在java中的使用
1.Neo4j访问的两种方式 嵌入式数据库服务器模式(通过REST的访问) 它是由应用程序的性质(neo4j是独立服务器 还是和程序在一起),性能,监控和数据安全性来决定架构选择。 An embedded database(嵌入式数据库) 嵌入式Neo4j数据库…...
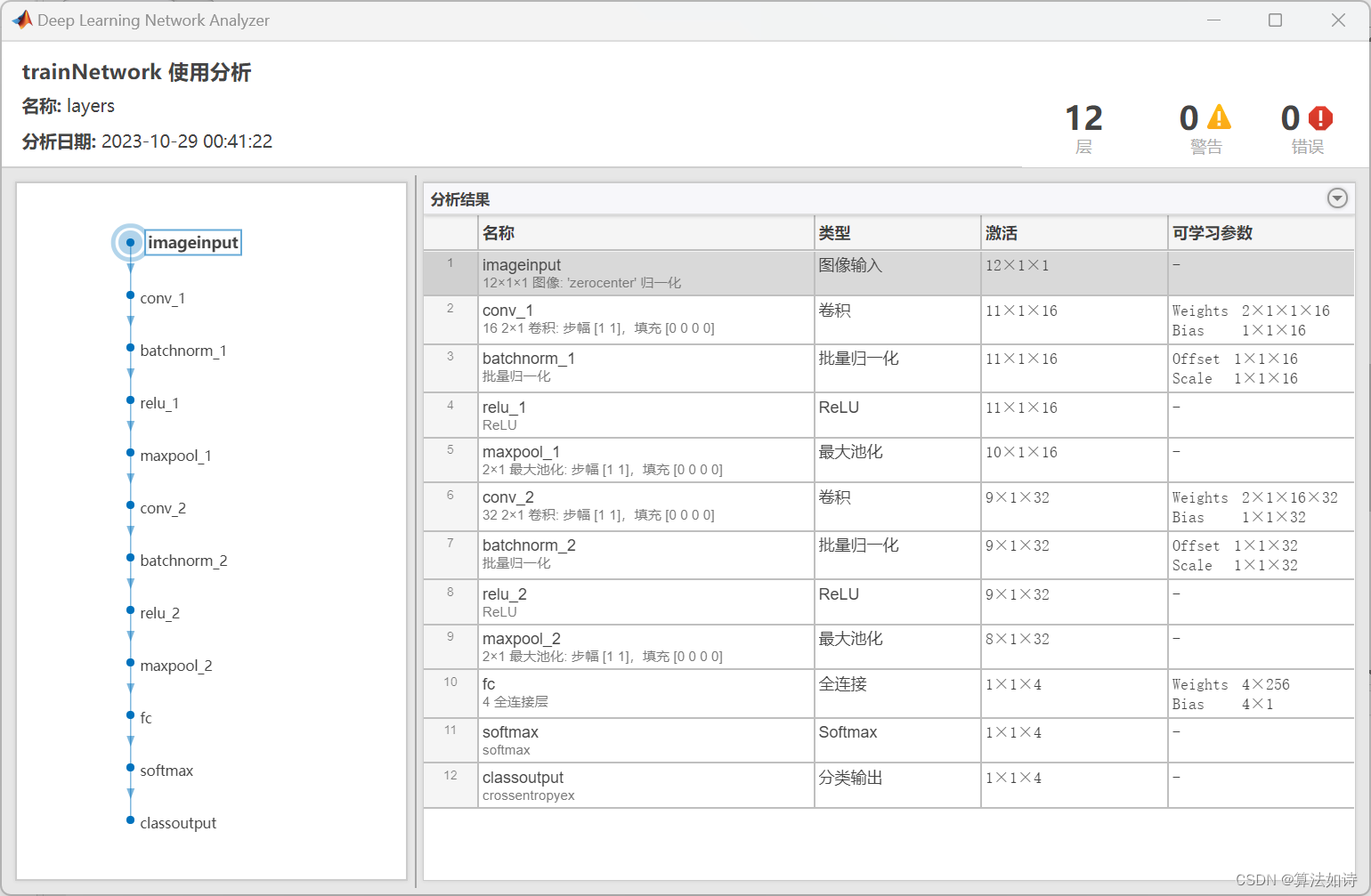
故障诊断 | 一文解决,CNN卷积神经网络故障诊断(Matlab)
文章目录 效果一览文章概述专栏介绍源码设计参考资料效果一览 文章概述 故障诊断 | 一文解决,CNN卷积神经网络故障诊断(Matlab) 专栏介绍 订阅【故障诊断】专栏,不定期更新机器学习和深度学习在故障诊断中的应用;订阅...

uniapp-app使用富文本编辑器editor
使用的是uniapp内置组件的表单组件editor:editor 组件 | uni-app官网 (dcloud.net.cn) editor 组件对应的 editorContext 实例:editorContext | uni-app官网 (dcloud.net.cn) 文档上写的也不是特别详细,还以为得npm,但没npm也能用…...

20240131 大模型快讯
//社区生态// 国内首个音视频多媒体大模型万兴“天幕”正式发布。万兴科技发布国内首个音视频多媒体大模型万兴“天幕”,支持多种语言,实现音视频创作闭环。 //行业落地// 全球首款搭载AI大模型的MPV智能座舱发布。江淮全新MPV瑞风RF8上市发布…...
存储引擎(2)MyISAM)
MySQL原理(二)存储引擎(2)MyISAM
一、MyISAM介绍 1、介绍: MyISAM引擎是MySQL5.5版本之前的数据库所默认的数据表引擎。每一个采用MyISAM引擎的数据表在实际存储中都是由三个文件组成,分别是frm文件保存表的结构,MYD文件保存表的数据、MYI文件保存表的索引,文件…...

P1088 [NOIP2004 普及组] 火星人题解
题目 人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言,但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的,首先,火星人把一个非常大的数字告诉人类科学家,科学家破解这个数…...

Python面向对象编程:探索代码的结构之美
文章目录 一、引言二、为什么学习面向对象编程2.1 提高代码的可维护性:通过封装、继承和多态实现模块化设计2.2 提升代码的复用性:通过类和对象的创建实现代码的重用 三、类和对象的基本概念3.1 类和对象的定义和关系:类是对象的模板…...
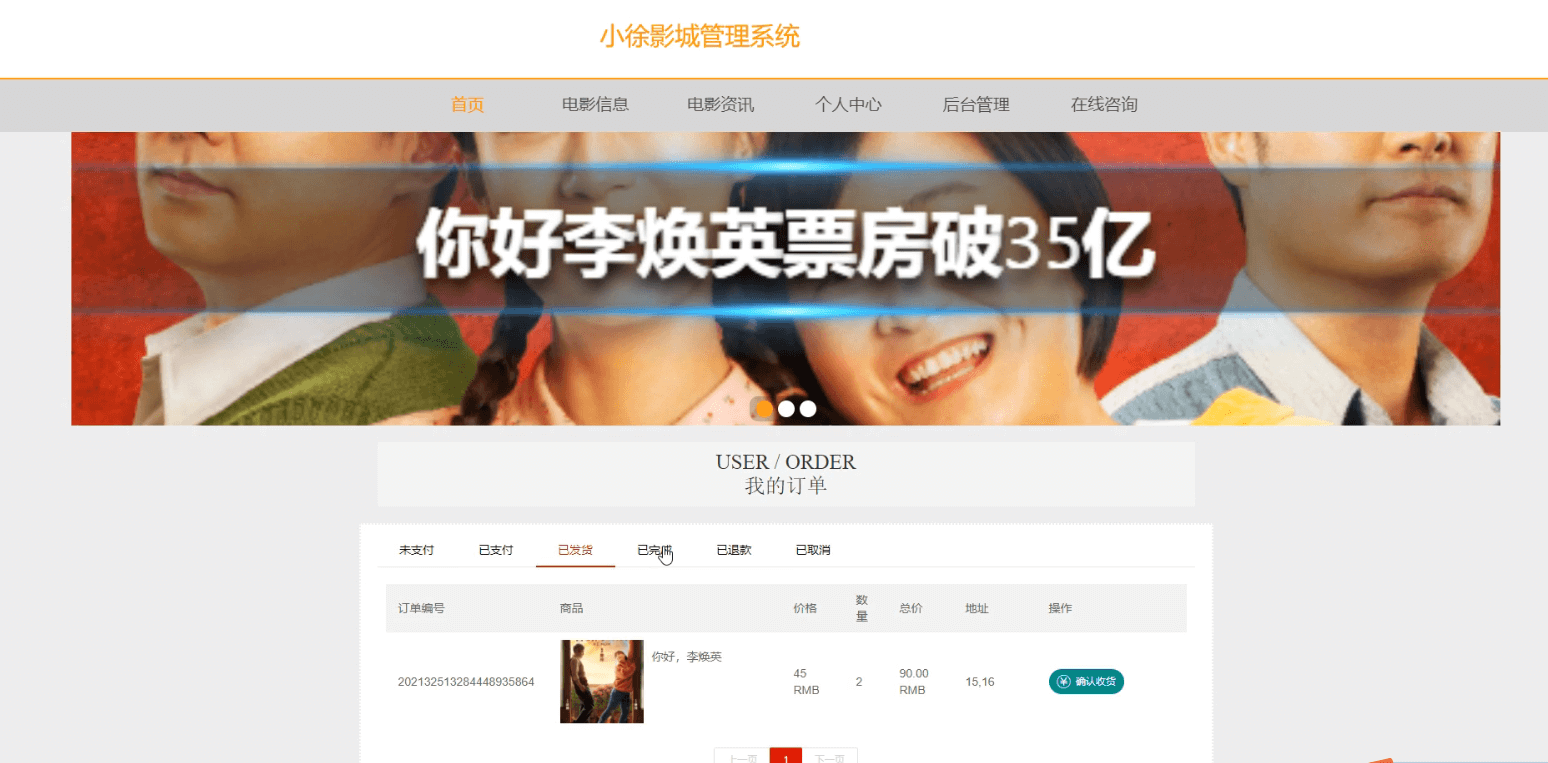
Java基于SpringBoot+Vue的电影影城管理系统,附源码,文档
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
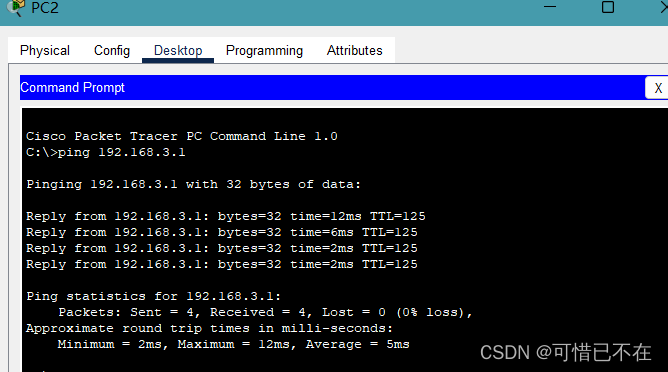
【学网攻】 第(14)节 -- 动态路由(EIGRP)
系列文章目录 目录 系列文章目录 文章目录 前言 一、动态路由EIGRP是什么? 二、实验 1.引入 实验步骤 实验拓扑图 实验配置 看到D开头是便是我们的EIGRP动态路由 总结 文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻】 第(2)节 -- 交换机认识及使用【学…...
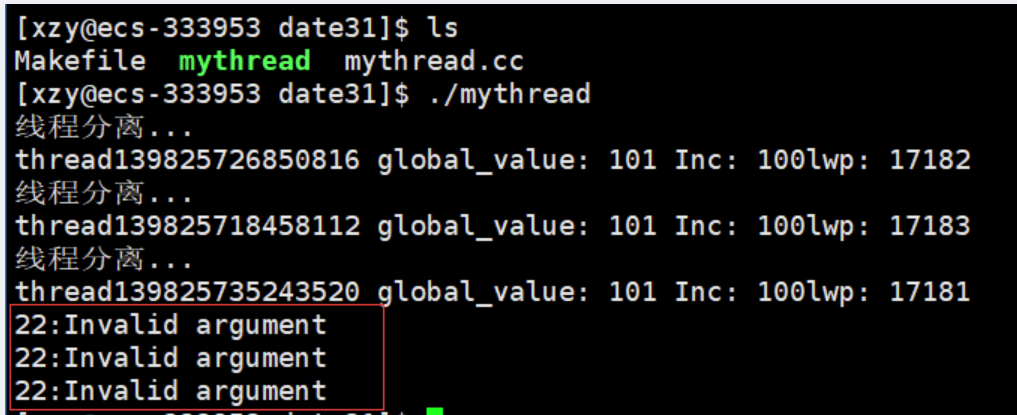
【Linux】多线程(线程概念+线程控制)
🌇个人主页:平凡的小苏 📚学习格言:命运给你一个低的起点,是想看你精彩的翻盘,而不是让你自甘堕落,脚下的路虽然难走,但我还能走,比起向阳而生,我更想尝试逆风…...

【昕宝爸爸小模块】深入浅出详解之常见的语法糖
深入浅出详解之常见的语法糖 一、🟢关于语法糖的典型解析二、🟢如何解语法糖?2.1🟢糖块一、switch 支持 String 与枚举2.2📙糖块二、泛型2.3📝糖块三、自动装箱与拆箱2.4🍁糖块四、方法变长参数…...

低代码
腾讯云微搭低代码 WeDa _低代码开发平台_可视化开发平台-腾讯云 首页 - 钉钉宜搭 快速上手多维表格 爱速搭 - 企业应用智能设计平台 | 低代码平台 - 百度智能云 Astro轻应用 Astro Zero_低代码开发平台_软件开发工具_应用开发工具_华为云 低代码是一种软件开发方法&#x…...

2024/1/30 备战蓝桥杯 3-1 栈
目录 小鱼的数字游戏 P1427 小鱼的数字游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 表达式括号匹配 P1739 表达式括号匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 【模板】栈 B3614 【模板】栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 小鱼的数字…...

qt setStyleSheet 设置多个属性{}之间用空格间隔
setStyleSheet 设置多个属性时,大属性之间不能用分号,用 空格进行间隔 pbtn1->setStyleSheet("QPushButton {background-color: rgb(4,138,224);font: bold 12pt;color: rgb(255,255,255);} QPushButton:hover,QPushButton:pushed {background-…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
