数据结构--树
一、树的基本术语
结点:树中的一个独立单元
结点的度:结点下分支的个数
树的度:树中所有结点中度的最大值
非终端结点:度不为0的结点
双亲和孩子:结点下的子树称为该结点的孩子.相应地,该结点称为孩子的双亲
兄弟:同一个双亲的孩子之间
祖先:从根到该结点所经分支上的所有结点
子孙:从某结点为根,其下直接或间接的结点
层次:从根开始,根的孩子为第二层,依次类推
堂兄弟:双亲在同一层的结点
树的深度:树中结点的最大层次称为树的深度或高度
有序树和无序树:如果将树中所有结点的各子树看成从左至右是有次序的,反之无序的为无序树(在有序树中最左边的子树的根称为第一个孩子最右边称为最后一个孩子)
森林m(m>=0)棵互不相交的树的集合
二、二叉树(Binary Tree)
1>有且仅有一个称为根的结点
2>除叶子结点,剩余每个结点可能有左孩子或右孩子(最多有两个)
二叉树具有天然递归结构
每个结点的左子树也是二叉树
每个结点的右子树也是二叉树
性质1:在二叉树的第i层上至多有2^(i-1)个结点(i>=1)
性质2:深度为k的二叉树至多有2^k-1个结点(k>=1)
性质3:对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0= n2+1(度为0的结点数比度为2的结点数多1)
三、二分搜索树
二分搜索树是二叉树
二分搜索树的每个结点的值(大于其左子树的所有结点的值|小于其右子树的所有结点的值)
每一棵子树也是二分搜索树
二分搜索树的相关操作
创建二分搜索树的类
// 保存在树中的结点必须具有可比性
public class BinearySearchTree<T extends Comparable<T>> {}
创建树的结点
private class Node<T> {private T ele;// 结点的值private int frequence;// 频率private Node<T> left, right;// 分别指向左右孩子的索引public Node(T ele) {this.ele = ele;this.frequence = 1;this.right = this.left = null;}}树对应的属性
private Node<T> root;// 树的根节点private int size;// 书中结点的个数构建树
public BinearySearchTree() {this.root = null;this.size = 0;}获取树中结点数
public int getSize() {return this.size;}向树中添加结点
public void add(T ele) {// 更新根节点this.root = addDG(this.root, ele);}// 语义:向以root为根的二分搜索树中添加元素eleprivate Node addDG(Node<T> root, T ele) {// 递归终止条件if (root == null) {this.size++;return new Node<T>(ele);}// 递归操作if (root.ele.compareTo(ele) > 0) {root.left = addDG(root.left, ele);} else if (root.ele.compareTo(ele) < 0) {root.right = addDG(root.right, ele);} else {// 更新频率root.frequence++;}return root;}查询某个值在树中是否存在
public boolean search(T ele) {return searchDG(this.root, ele);}// 语义:从以root为根的二分搜索树中查找元素eleprivate boolean searchDG(Node<T> root, T ele) {// 递归终止条件if (root == null) {return false;}// 递归操作if (root.ele.compareTo(ele) == 0) {return true;} else if (root.ele.compareTo(ele) > 0) {return searchDG(root.left, ele);} else {return searchDG(root.right, ele);}}二分搜索树的先序遍历
public void preTravel() {List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();preTravelDG(this.root, list);String resStr = list.stream().map(item -> "[" + item.getKey() + ":" + item.getValue() + "]").collect(Collectors.joining("-"));System.out.println(resStr);}// 先序遍历以root为根的树,将结果保存在list中private void preTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {// 递归终止条件if (root == null) {return;}// 递归操作list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));// 遍历左子树preTravelDG(root.left, list);// 遍历右子树preTravelDG(root.right, list);}二分搜索树的中序遍历
public void midTravel() {List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();midTravelDG(this.root, list);String resStr = list.stream().map(item -> "[" + item.getKey() + ":" + item.getValue() + "]").collect(Collectors.joining("-"));System.out.println(resStr);}// 中序遍历以root为根的树,将结果保存在list中private void midTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {// 递归终止条件if (root == null) {return;}// 递归操作// 遍历左子树midTravelDG(root.left, list);list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));// 遍历右子树midTravelDG(root.right, list);}二分搜索树的后序遍历
public void sufTravel() {List<AbstractMap.SimpleEntry<T, Integer>> list = new ArrayList<>();sufTravelDG(this.root, list);String resStr = list.stream().map(item -> "[" + item.getKey() + ":" + item.getValue() + "]").collect(Collectors.joining("-"));System.out.println(resStr);}// 后序遍历以root为根的树,将结果保存在list中private void sufTravelDG(Node<T> root, List<AbstractMap.SimpleEntry<T, Integer>> list) {// 递归终止条件if (root == null) {return;}// 递归操作// 遍历左子树sufTravelDG(root.left, list);// 遍历右子树sufTravelDG(root.right, list);list.add(new AbstractMap.SimpleEntry<>(root.ele, root.frequence));}层序遍历(依赖队列)
public void levelTravel() {// 判断树是否为空if (this.isEmpty()) {return;}Queue<AbstractMap.SimpleEntry<Node<T>, Integer>> queue = new LinkedList<>();// 1.现将根节点入队queue.add(new AbstractMap.SimpleEntry<>(this.root, 1));// 2.遍历队列while (!queue.isEmpty()) {// 2-1 出队AbstractMap.SimpleEntry<Node<T>, Integer> pair = queue.poll();// 结点Node<T> node = pair.getKey();// 层int level = pair.getValue();System.out.println("[val:" + node.ele + ",level:" + level + "]");// 2-2 判断左右子树是否为空if (node.left != null) {queue.add(new AbstractMap.SimpleEntry<>(node.left, level + 1));}if (node.right != null) {queue.add(new AbstractMap.SimpleEntry<>(node.right, level + 1));}}}判断是否为空
public boolean isEmpty() {return this.size == 0;}寻找树中最小元素
public T getMinValue() {if (this.isEmpty()) {return null;}Optional<Node<T>> optional = getMinNode(this.root);return optional.get().ele;}// 语义:在以Node为根结点的树中查找最小结点private Optional<Node<T>> getMinNode(Node<T> node) {// 递归终止的条件if (node.left == null) {return Optional.of(node);}// 递归操作return getMinNode(node.left);}寻找树中最大元素
public T getMaxValue() {if (this.isEmpty()) {return null;}Optional<Node<T>> optional = getMaxNode(this.root);return optional.get().ele;}// 语义:在以Node为根结点的树中查找最大结点private Optional<Node<T>> getMaxNode(Node<T> node) {// 递归终止的条件if (node.right == null) {return Optional.of(node);}// 递归操作return getMaxNode(node.right);}删除最小结点
public T removeMinNode() {T result = getMinValue();if (result == null) {return null;}// 更新根节点this.root = removeMinNode(this.root);return result;}/*** 语义:从以node为根的二分搜索树中删除元素最小的结点** @param node 树的根结点* return 删除最小结点之后的树的根结点*/private Node<T> removeMinNode(Node<T> node) {// 递归终止条件if (node.left == null) {// 删除操作// 1.记录右子树Node<T> rightTree = node.right;// 2.失去关联关系node.right = null;// 3.更新sizethis.size--;return rightTree;}// 递归操作node.left = removeMinNode(node.left);return node;}删除最大结点
public T removeMaxNode() {T result = getMaxValue();if (result == null) {return null;}// 更新根节点this.root = removeMaxNode(this.root);return result;}/*** 语义:从以node为根的二分搜索树中删除元素最大的结点** @param node 树的根结点* return 删除最大结点之后的树的根结点*/private Node<T> removeMaxNode(Node<T> node) {// 递归终止条件if (node.right == null) {// 删除操作// 1.记录左子树Node<T> leftTree = node.left;// 2.失去关联关系node.left = null;// 3.更新sizethis.size--;return leftTree;}// 递归操作node.right = removeMaxNode(node.right);return node;}删除任意结点
public void remove(T ele) {// 根据值查找结点this.root = remove(this.root, ele);}private Node<T> remove(Node<T> node, T ele) {// 递归终止条件// 没有找到的情况if (node == null) {return null;}// 找到了删除的结点if (node.ele.compareTo(ele) == 0) {this.size--;// node就是要删除的结点 // 1.左子树空,右子树不为空if (node.left == null) {Node<T> rightNode = node.right;node.right = null;return rightNode;} else if (node.right == null) {// 2.右子树空,左子树不为空Node<T> leftNode = node.left;node.left = null;return leftNode;} else {// 3.左右子树都不为空// 3-1从右子树中找最小结点Node<T> suffixNode = getMinNode(node.right).get();// 从右子树中删除最小结点suffixNode.right = removeMinNode(node.right);suffixNode.left = node.left;// 将node结点的左右子树失去关联关系node.left = node.right = null;this.size++;return suffixNode;}}// 递归操作if (node.ele.compareTo(ele) > 0) {node.left = remove(node.left, ele);} else {node.right = remove(node.right, ele);}return node;}删除根结点
public void removeRoot() {if (this.root == null) {return;}remove(this.root.ele);}相关文章:

数据结构--树
一、树的基本术语 结点:树中的一个独立单元 结点的度:结点下分支的个数 树的度:树中所有结点中度的最大值 非终端结点:度不为0的结点 双亲和孩子:结点下的子树称为该结点的孩子.相应地,该结点称为孩子的双亲 兄弟:同一个双亲的孩子之间 祖先:从根到该结点所经分支上的所…...

计算机网络_1.3电路交换、分组交换和报文交换
1.3电路交换、分组交换和报文交换 一、电路交换1、“电路交换”例子引入2、电路交换的三个阶段3、计算机之间的数据传送不适合采用电路交换 二、分组交换1、发送方(1)报文(2)分组(3)首部 2、交换节点3、接收…...

【AI视野·今日NLP 自然语言处理论文速览 第七十七期】Mon, 15 Jan 2024
AI视野今日CS.NLP 自然语言处理论文速览 Mon, 15 Jan 2024 Totally 57 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Machine Translation Models are Zero-Shot Detectors of Translation Direction Authors Michelle Wastl, Ja…...

神经网络的一些常规概念
epoch:是指所有样本数据在神经网络训练一次(单次epoch(全部训练样本/batchsize)/iteration1)或者(1个epochiteration数 batchsize数) batch-size:顾名思义就是批次大小,也就是一次训练选取的样…...
【从零开始的rust web开发之路 三】orm框架sea-orm入门使用教程
【从零开始的rust web开发之路 三】orm框架sea-orm入门使用教程 文章目录 前言一、引入依赖二、创建数据库连接简单链接连接选项开启日志调试 三、生成实体安装sea-orm-cli创建数据库表使用sea-orm-cli命令生成实体文件代码 四、增删改查实现新增数据主键查找条件查找查找用户名…...

SQL中limit的用法
在SQL中,LIMIT是一个用于限制返回结果行数的关键词。它可用于在查询结果中指定返回的行数,从而可以用于分页查询或限制结果集大小。 LIMIT关键词有两种常用的语法格式: LIMIT offset, count:该语法用于指定返回结果的起始位置和…...
vue3 [Vue warn]: Unhandled error during execution of scheduler flush
文章目录 前言一、报错截图二、排除问题思路相关问题 Vue3 优雅解决方法异步组件异同之处:好处:在使用异步组件时,有几个注意点: vue3 定义与使用异步组件 总结 前言 Bug 记录。开发环境运行正常,构建后时不时触发下面…...

【vue2源码】阶段一:Vue 初始化
文章目录 一、项目目录1、主目录2、打包入口 二、构造函数Vue的初始化1、创建 Vue 构造函数2、初始化内容分析2.1 initMixin2.2 stateMixin2.3 eventsMixin2.4 lifecycleMixin2.5 renderMixin 一、项目目录 源码版本:2.7.16 1、主目录 src |-- compiler # 包…...
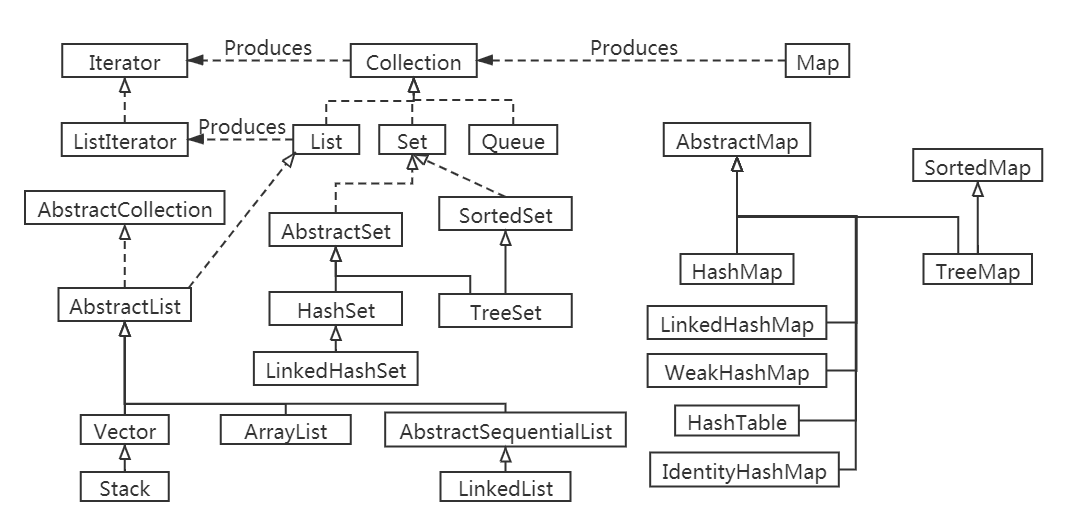
14.java集合
文章目录 概念Collection 接口概念示例 Iterator 迭代器基本操作:并发修改异常增强循环遍历数组:遍历集合:遍历字符串:限制 list接口ListIteratorArrayList创建 ArrayList:添加元素:获取元素:修…...
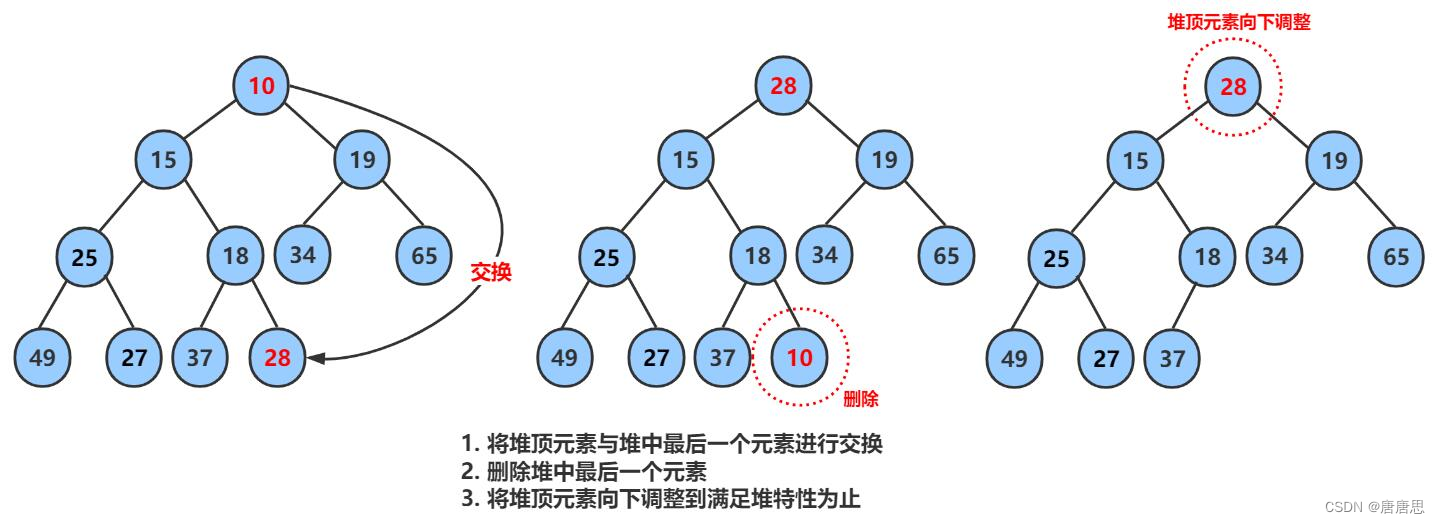
二叉树顺序结构堆实现
目录 Test.c测试代码 test1 test2 test3 🎇Test.c总代码 Heap.h头文件&函数声明 头文件 函数声明 🎇Heap.h总代码 Heap.c函数实现 ☁HeapInit初始化 ☁HeapDestroy销毁 ☁HeapPush插入数据 【1】插入数据 【2】向上调整Adjustup❗ …...

正则表达式 与文本三剑客(sed grep awk)
一,正则表达式 (一)正则表达式相关定义 1,正则表达式含义 REGEXP: Regular Expressions,由一类特殊字符及文本字符所编写的模式,其中有些字符(元字符)不表示字符字面意…...
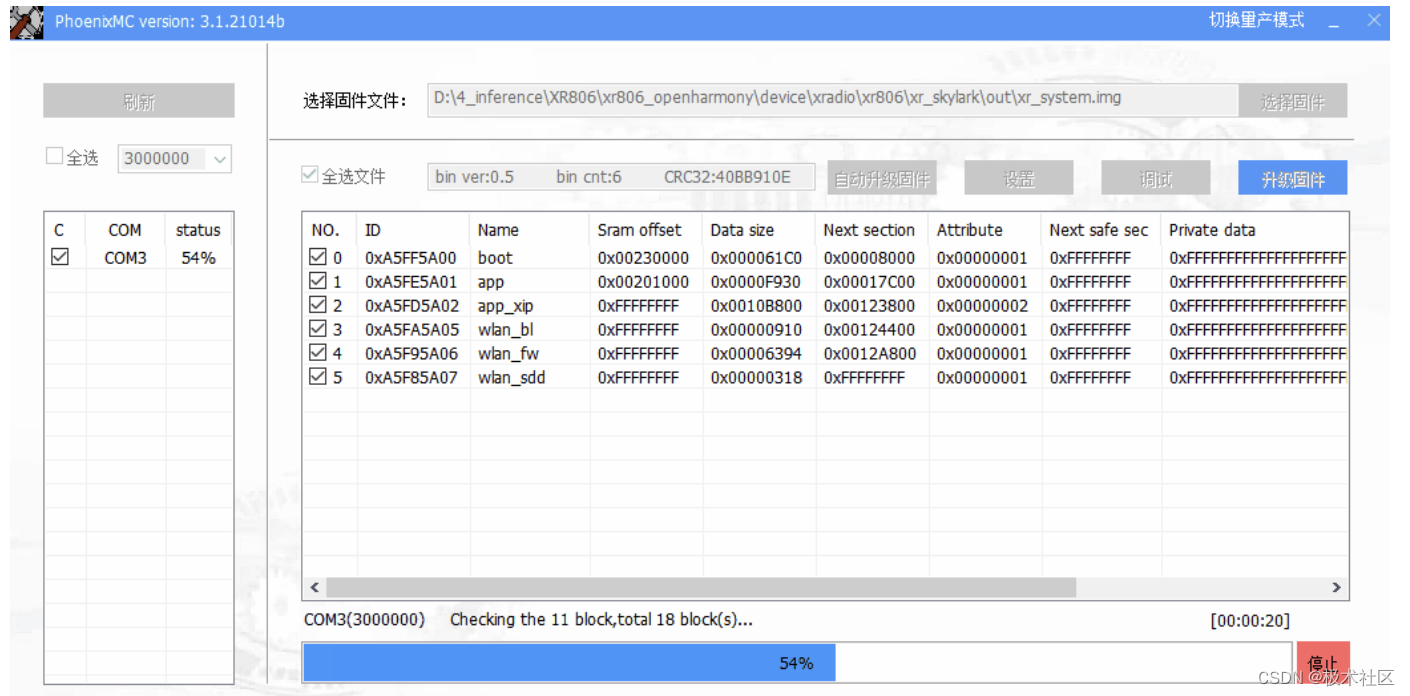
【XR806开发板试用】全志 XR806 OpenHarmony 鸿蒙系统固件烧录
大家好,我是极智视界,本教程详细记录了全志 XR806 OpenHarmony 鸿蒙系统固件烧录的方法。 在上一篇文章《【嵌入式AI】全志 XR806 OpenHarmony 鸿蒙系统固件编译》中咱们已经编译生成了系统镜像,这里把这个编译出来的镜像烧录到 XR806 板子里…...
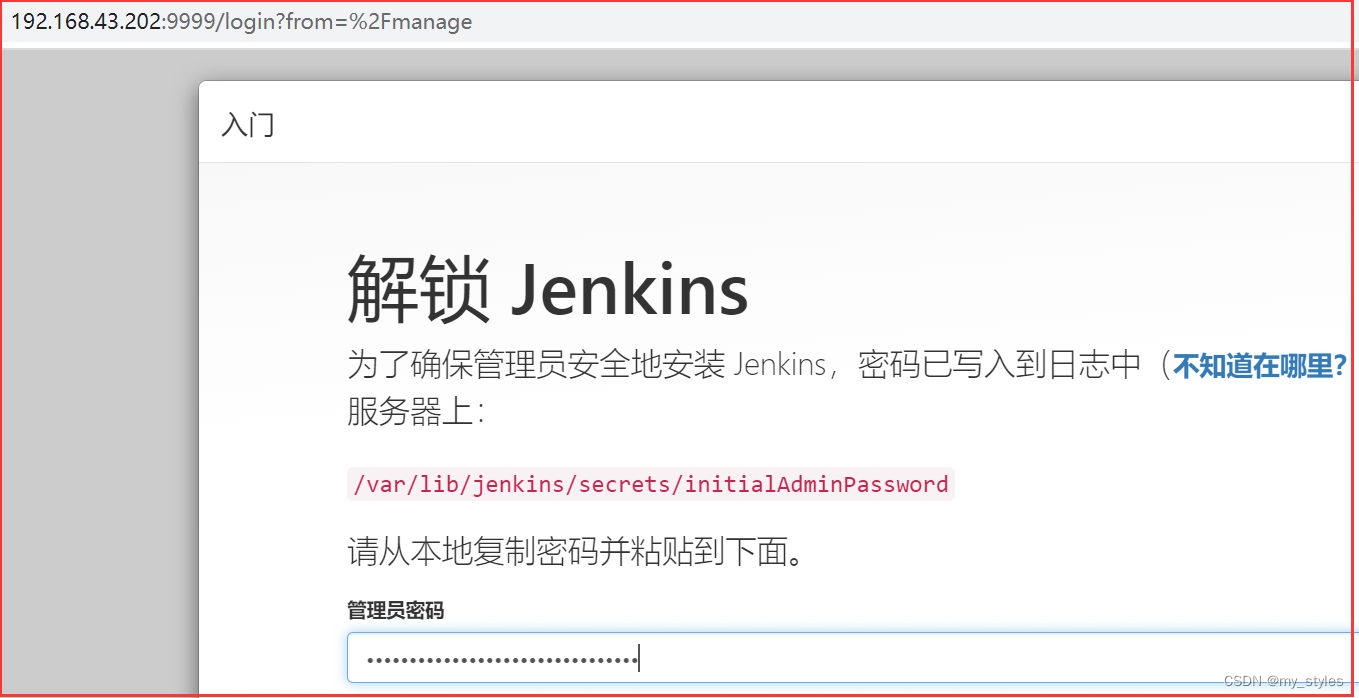
linux环境安装git、maven、jenkins等
重启 jenkins的命令: systemctl start jenkins 如果没有vim 命令 可以使用 yum install vim 安装 vim git 下载包地址 https://www.kernel.org/pub/software/scm/git/git-2.28.0.tar.gz 1.安装依赖环境: yum install -y curl-devel expat-devel ge…...

RabbitMQ快速上手
首先他的需求实在什么地方。我美哟明显的感受到。 它给我的最大感受就是脱裤子放屁——多此一举,的感觉。 他将信息发送给服务端中间件。在由MQ服务器发送消息。 服务器会监听消息。 但是它不仅仅局限于削峰填谷和稳定发送信息的功能,它还有其他重要…...

SpringBoot activemq收发消息、配置及原理
SpringBoot集成消息处理框架 Spring framework提供了对JMS和AMQP消息框架的无缝集成,为Spring项目使用消息处理框架提供了极大的便利。 与Spring framework相比,Spring Boot更近了一步,通过auto-configuration机制实现了对jms及amqp主流框架…...

视频智能识别安全帽佩戴系统-工地安全帽佩戴识别算法---豌豆云
视频智能识别安全帽佩戴系统能够从繁杂的工地、煤矿、车间等场景下同时对多个目标是否戴安全帽穿反光衣进行实时识别。 当视频智能识别安全帽佩戴系统发现作业人员没有戴安全帽、穿反光衣或者戴安全带,系统会及时报警提醒,并抓拍存档。 视频智能识别安…...
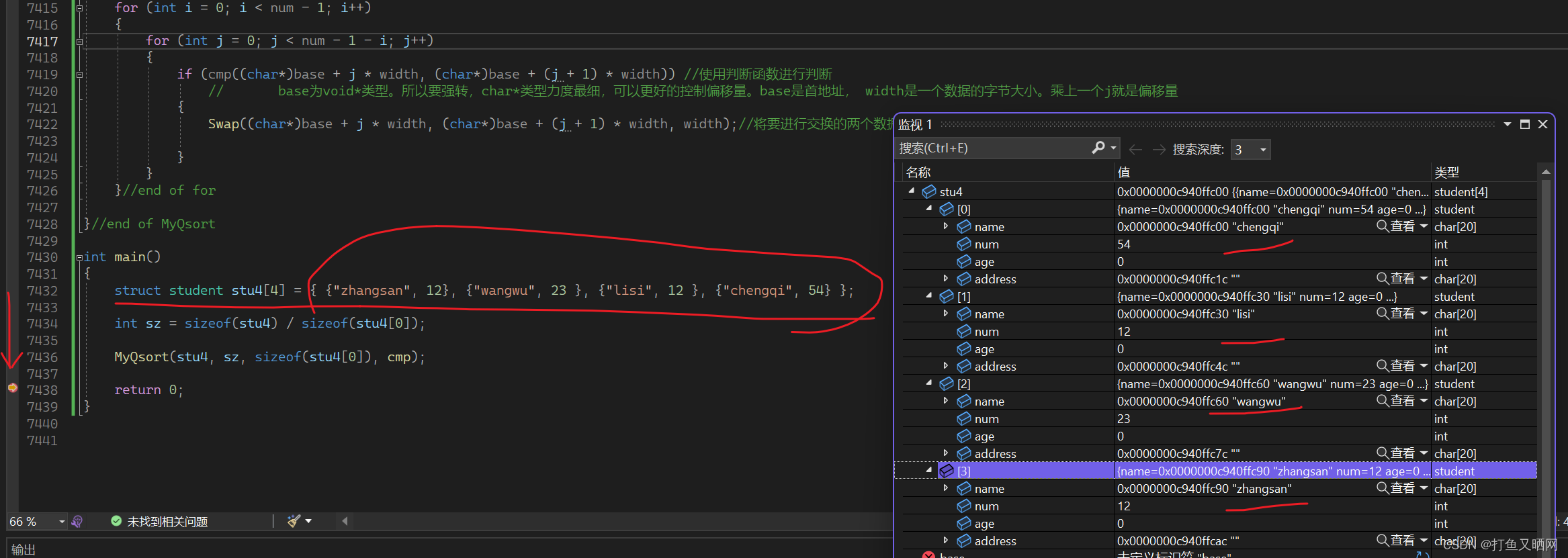
指针的深入理解(三)
这一节主要使用复习回调函数, 利用冒泡模拟实现qsort函数。 qsort 排序使用冒泡排序,主要难点在于运用元素个数和字节数以及基地址控制元素的比较: if里面使用了一个判断函数,qsort可以排序任意的数据,原因就是因为可…...

【Linux C | 网络编程】详细介绍 “三次握手(建立连接)、四次挥手(终止连接)、TCP状态”
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...
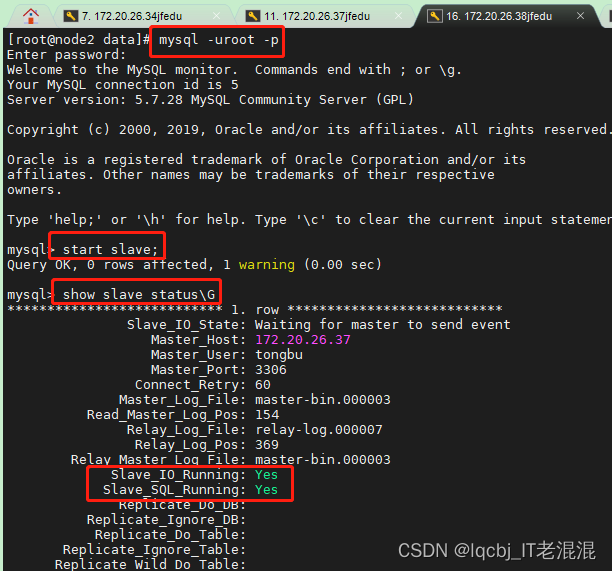
主从数据库MySQL服务重启步骤与注意事项
主从数据库MySQL服务重启步骤与注意事项 实验环境: 172.20.26.34 (主应用服务器) 172.20.26.26 (备应用服务器) 172.20.26.37 (主库服务器) 172.20.26.38 (从库服务器&…...

netlink学习
netlink是什么 netlink是Linux内核中的一种进程间通信(IPC)机制。它允许内核空间与用户空间之间,以及用户空间进程之间进行双向通信。 内核里的很多子系统使用netlink通信,包括网络管理(Routing,Netfilt…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
