自然数学的哲学原理--复数理论的扩展
自然数学的哲学原理--复数理论的扩展
2023-03-05 10:27:12
自然数学的哲学原理--复数理论的扩展
一维:线,实数
二维:平面
三维:立体
四维:相对论时空
复数,以一个数对形式表示,实现了复平面的表示a+bi
复数扩展:以一个数表示立体:a+bi+cii
再扩展:a+bi+cii+diii表示四维时空点
倒推:0维,-1维,-2维
-2维:自然数N(自然数,0,负数,不理数)
-1维:自然数对NM,表示有理数n/m,称为有理数平面
所以,有理数n/m可以表示为,n+mi形式
无理数映像时间,时间不是空间能表示的。无理数不是有理数能表示的。
无理数,可以表示为(超越数是不能作为有理系数多项式方程的根的数,定义恰与代数数相反。)
无理数可以用有理数来趋近,映像映射相对论中的洛伦滋公式,时间与空间是有关联的。
0维:有理数a,与无理数b,a+bi映像实数,映像四维时空复数扩展,a+bi+cii+diii表示四维时空点
0维,-1维,-2维,哲学或称为太极,无极,空极
在一维世界,看到,太极,无极,空极的复数表示,是一个实点来的
所以,哲学上或猜测,二维三维的复数扩展,在这个世界看到是平面立体,在四维时空看到的可能是一个实点来的,
由此哲学猜测,低维的复数形式,在高维是一个实点
1.再扩展:整数作为全集或猜想分成自然数与负数与0,其中,负数=f(自然数1,自然数2),
2.再扩展:自然数作为全集或猜想分成质数与合数与1,其中,合数=f(质数1,质数2),或正是哥德巴赫猜想,
3.再扩展:质数作为全集或猜想又内分成N+M+2,其中,M=f(n1,n2)正相关,这个可能与素数公式有关,这个未解决也。
4.再扩展:实数作为全集,分成整数与有理数(去整数),与无理数(作为组合全集之补集特殊),其中 有理数=f(整数1,整数2)
复数a+bi即f(a,b),i为-1的根号√-1,负数为-1本身,都与-1有关,无理数与-1无关,
但都是原有理论无法解释,扩展包含而成
有点映像,水浒中招安土匪而来
相关文章:

自然数学的哲学原理--复数理论的扩展
自然数学的哲学原理--复数理论的扩展 2023-03-05 10:27:12 自然数学的哲学原理--复数理论的扩展 一维:线,实数 二维:平面 三维:立体 四维:相对论时空 复数,以一个数对形式表示,实现了复平面的…...

tsconfig.json中的一些配置
compilerOptions 编译选项是配置文件中非常重要也比较复杂的配置选项 target:设置ts代码编译的目标版本 可选值: ES3(默认)、ES5、ES6/ES2015、ES7/ES2016、ES2017、ES2018、ES2019、ES2020、 ESNext 示例: &quo…...

Spark调优总结
下面是基于官方优化建议,加上自己的一些理解整理。官方地址:https://spark.apache.org/docs/2.4.8/tuning.html 任务并行度 Spark会根据每个文件的大小自动设置运行“map”任务的数量,而对于分布式的“reduce”操作,例如groupBy…...
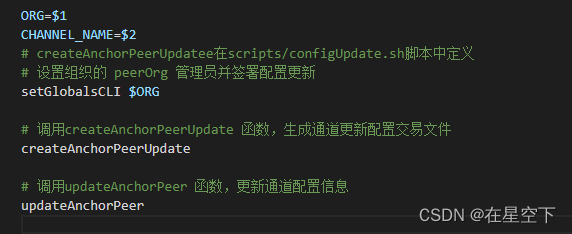
4.创建和加入通道相关(network.sh脚本createChannel函数分析)[fabric2.2]
fabric的test-network例子有一个orderer组织、两个peer组织、每个组织一个节点,只有系统通道(system-channel),没有其他应用通道。我们可以使用./network.sh createChannel命令来创建一个名为mychannel的应用通道。 一、主要概念 …...
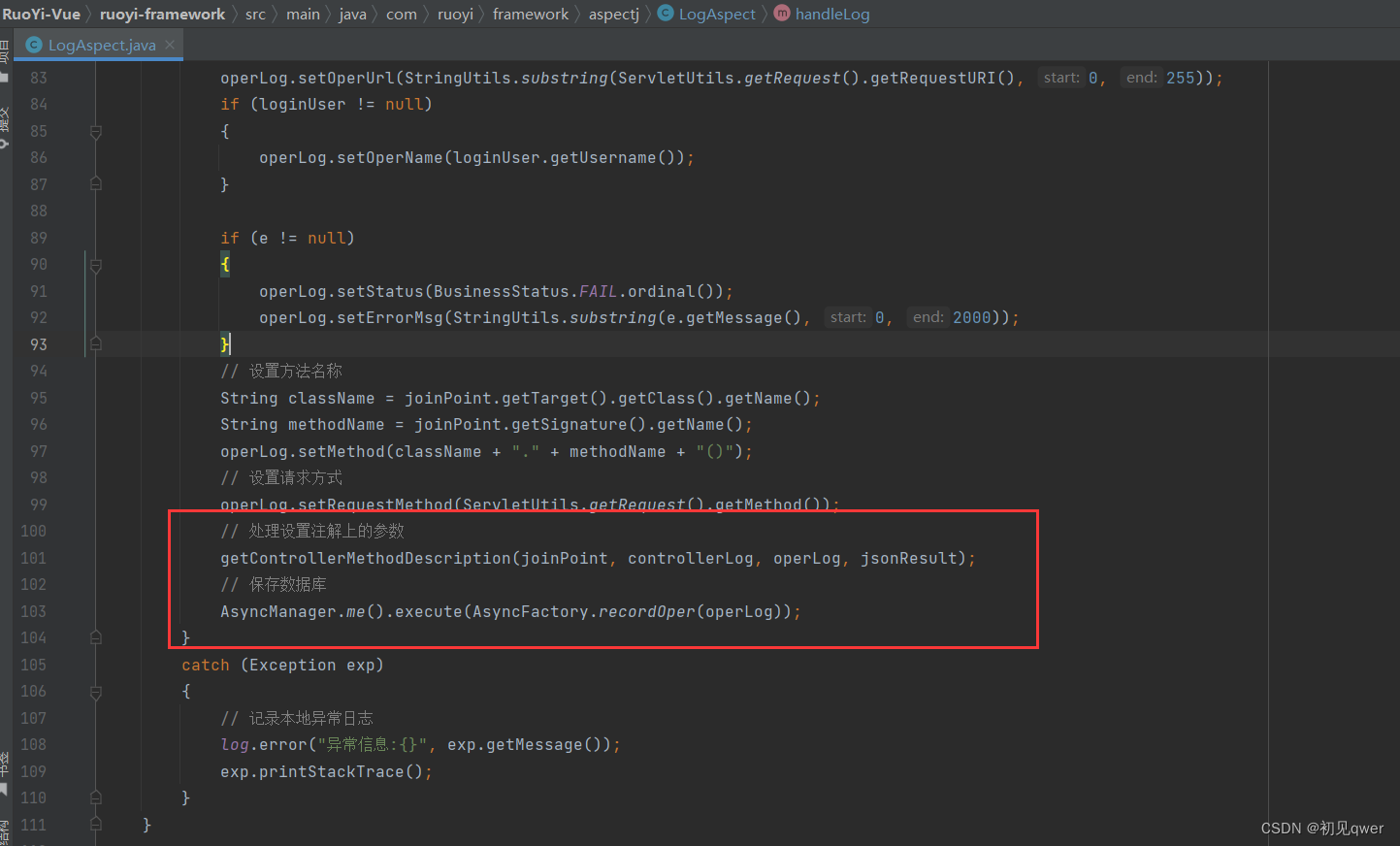
若依学习(前后端分离版)——自定义注解@Log(如何自定义注解,实现aop)
如何自定义注解 aop的基本知识与应用 若依对用户的一些更新删除等敏感操作操作进行了日志记录 注解定义和切面处理的项目位置 第一步:自定义注解log 定义了注解的相关信息。这里定义的属性可以在使用时加以定义 注解Target和Retention的作用 第二步切面逻辑…...

防止暴力破解ssh的四种方法
一. 方法介绍 防止暴力破解的四种方法: 1 密码要写的足够的复杂,通常建议将密码写16位,并且无连贯的数字或者字母;当然也可以固定一个时间修改一次密码,推荐是一个月修改一次会稳妥一些2 修改ssh的端口号,…...
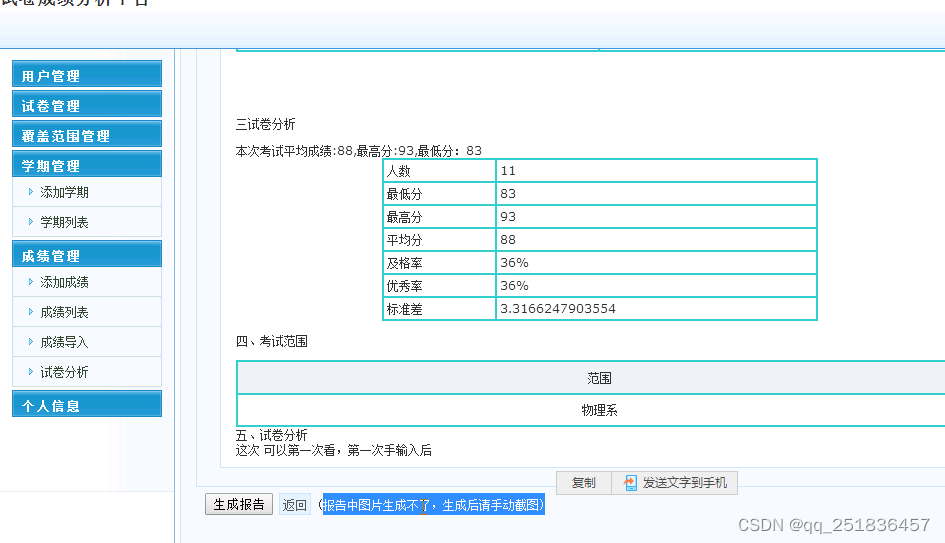
jsp试卷分析管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP试卷分析管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…...
可选链运算符(?.)与空值合并运算符(??)
1. 可选链运算符Optional chaining(?.) MDN定义 可选链运算符(?.)允许读取位于连接对象链深处的属性的值,而不必明确验证链中的每个引用是否有效。?. 运算符的功能类似于 . 链式运算符,不同之处在于,在引用为空 (n…...

JavaScript 闭包
JavaScript 变量可以是局部变量或全局变量。私有变量可以用到闭包。全局变量函数可以访问函数内部定义的变量,如:实例function myFunction() {var a 4;return a * a;}尝试一下 函数也可以访问函数外部定义的变量,如:实例var a 4…...

每日记录自己的Android项目(二)—Viewbinding,WebView,Navigation
今日想法今天是想把做一个跳转页面的时候调到H5页面去,但是这个页面我用app来承载,不要调到浏览器去。所以用到了下方三个东西。Viewbindingbuild.gradle配置首先在app模块的build.gradle里添加一下代码默认情况下,每一个布局xml文件都会生成…...

20230305英语学习
Climate Change Is Suffocating Large Parts of the Ocean 研究:气候变化正在使海洋“缺氧” One day more than a decade ago, Eric Prince was studying the tracks of tagged fish when he noticed something odd.Blue marlin off the southeastern United State…...
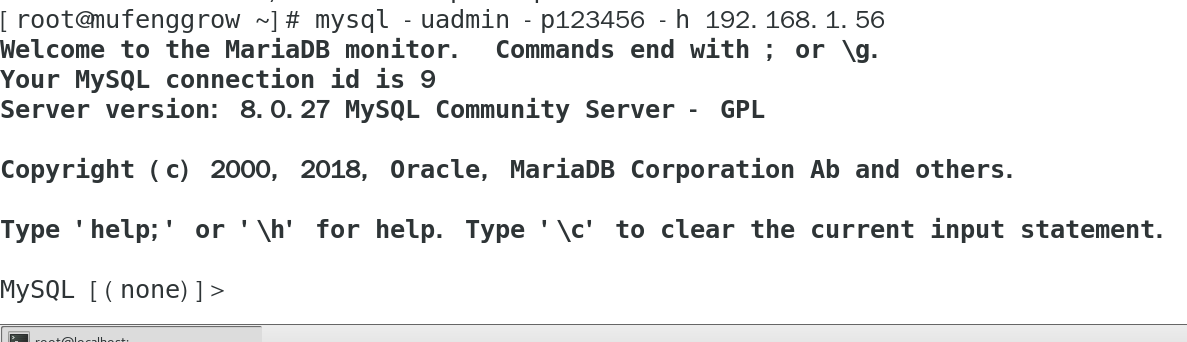
【Linux】手把手教你在CentOS上使用docker 安装MySQL8.0
文章目录前言一. docker的安装1.1 从阿里下载repo镜像1.2 安装docker1.3 启动docker并查看版本二. 使用docker安装MySQL8.02.1 拉取MySQL镜像2.2 创建容器2.3 操作MySQL容器2.4 远程登录测试总结前言 大家好,又见面了,我是沐风晓月,本文主要…...

论文解读:High Dynamic Range and Super-Resolution from Raw Image Bursts
论文解读:High Dynamic Range and Super-Resolution from Raw Image Bursts 今天介绍一篇发表于 2022 年 ACM Tranaction on Graphic 上的文章,这篇文章通过多帧曝光将 HDR 与 SR 放在一起解决,与一般的文章不同的地方在于,这篇文…...
国内的PMP考试通过率高达97%?
自认为是虚高,虽然国人在考试方面的确独树一帜的强,应该也没有这样夸张。 如果自学,大概是50%,如果有老师教,那大概是60%到80%,还是比较高的。 为什么自学那么低?除了自身的自制力的问题&…...

IOC(概念和原理)
文章目录1. IOC容器概念2. IOC底层原理3. IOC(接口)4. IOC操作Bean管理(概念)5. IOC操作Bean管理(基于xml方式)5.1 基于xml创建对象5.2 基于xml方式注入属性5.2.1 DI:依赖注入,就是注…...

操作系统 - 第二章
一、进程的定义、组成、组织、特征 一、进程的定义 从不同的角度,进程有不同的定义 1、进程是程序的一次执行过程; 2、进程是一个程序及其数据在处理机上顺序执行时所发生的活动; 3、进程是具有独立功能的程序在数据集合上运行的过程…...

进程控制~
进程控制 (创建、终止,等待,程序替换) 进程创建: pid_t fork();父子进程,数据独有,代码共享,各有各的地址 pit_t vfork();父进程阻塞,直到子进程exit退出或者程序替换之…...
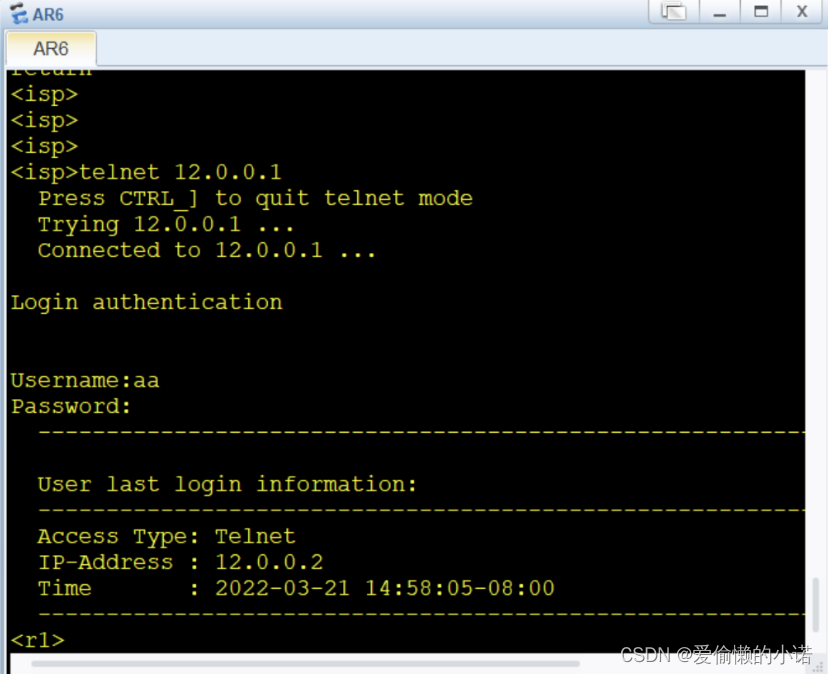
HCIP第一个实验
实验要求与实验拓扑子网划分分析将骨干链路看成一个整体,路由器后的2个环回地址先看成一个,最后再进行拆分。计算得出,一共需要划分为6个子网段,取三位。再将每一条网段,按照题目要求进行划分最后完成子网划分。子网划…...
)
阿里云轻量服务器--Docker--dubbo-admin安装(连接zookeeper nacos)
前言:当使用dubbo 作为微服务的接口调用,在dubbo 注册到zookeeper 或者nacos 中时 可以安装dubbo-admin 作为服务的监测; 1 Dubbo Admin 介绍: Dubbo 框架提供了丰富的服务治理功能如流量控制、动态配置、服务 Mock、服务测试等…...

树莓派Pico W无线WiFi开发板使用方法及MicroPython编程实践
树莓派Pico W开发板是树莓派基金会于2022年6月底推出的一款无线WiFi开发板,它支持C/C和MicroPython编程。本文介绍树莓派Pico W无线WiFi开发板的使用方法及MicroPython编程示例,包括树莓派Pico W开发板板载LED使用及控制编程示例,Pico W开发板…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
