【现代密码学基础】详解完美安全与香农定理
目录
一. 介绍
二. 完美安全的密钥与消息空间
三. 完美安全的密钥长度
四. 最优的完美安全方案
五. 香农定理
(1)理论分析
(2)严格的正向证明
(3)严格的反向证明
六. 小结
一. 介绍
一次一密方案,英语写做one time pad encryption scheme
一次一密方案可以实现完美安全(perfectly secret),但是这些方案是有局限性的,比如所有完美安全的方案密钥空间都要大于等于消息空间,这个定理待会我们会利用密码学专业术语进行证明。
如果假定密钥的长度固定,消息空间(message space)里的明文长度也固定的话,那么完美安全就要求密钥的长度大于等于消息的长度。当然,如果密钥和消息长度一样的话,就像一次一密那样,则是最优的情况。
除了这一个限制外,完美安全还要求密钥只能使用一次,具体证明则留给读者了。
二. 完美安全的密钥与消息空间
一个密码方案可以抽象成如下三个算法:
Gen,Enc,Dec
如果说该密码方案是完美安全的,他的消息空间为M,密钥空间为K,那么一定可得:
证明:
此处我们利用反证法。也就是证明,如果|K|<|M|,那么该方案一定不是完美安全的。
首先假定|K|<|M|。
不妨假设明文在M上是均匀分布的。从密文空间C中选择一个密文c,并且该密文的概率不为0,也就是:
对于该密文c来讲,使用不同的密钥k可能会得到不同的明文。我们将所有的可能性形成一个集合称之为M(c),如下:
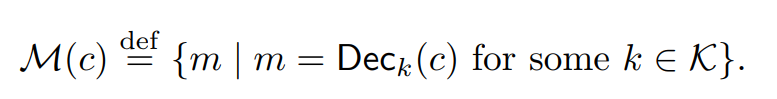
并不是每个密钥解密都有效,所以很容易可得该集合的空间小于等于密钥的空间,注意包含等于号就是恰好每个密钥都有效,那么可得:
大家可以把该过程的解密算法看成是确定性算法(deterministic)。
根据我们的条件假设,密钥空间小于明文空间,也就是|K|<|M|,那么必然存在一部分的明文不在该集合中,也就是:
所以可得:
![]()
该概率代表已知密文c,不可能会解密得到m',因为你已经尝试了所有的密钥。
但是m'在明文空间中是有概率的,也就可以得到:
![]()
从敌手的角度来讲,这就是泄露的信息。在已知密文情况下,明文的信息被泄露了一部分。所以很明显该方案不是完美安全的。
三. 完美安全的密钥长度
以上讨论告诉我们,完美安全不能无限降低密钥的长度,也可以将其看成完美安全的局限性。当然,现如今总是会出现一些非密码学的文章解释说设计出了一个新的加密方案,方案是无法攻破的,并且实现了类似一次一密的安全性,而且密钥的长度还小于明文的长度。很明显这类说法要么就是非严格密码学的局外人,要么就是方案本身是错的。
四. 最优的完美安全方案
在香农(Shannon)对完美安全的解释工作中,他指出密钥生成算法Gen要从所有可能的密钥中均匀输出密钥,就像一次一密方案。对于任意的明文m和密文c,都会存在唯一的密钥来匹配m和c,这个和一次一密方案也很类似。
这些有用的特征都可以用来证明方案的完美安全。换句话说,明文,密文和密钥的尺寸都是相等的,也就是:
|M|=|K|=|C|
在之前的证明中,我们已经严格证明完美安全要求:
借助映射定理,要想解密算法不出错,则要保证密文空间要大于等于明文空间,也就是:
通过以上的这些讨论我们不难得出,最优的完美安全方案需要保证:
|M|=|K|=|C|
五. 香农定理
将加密方案表示成:
(Gen,Enc,Dec)
其中消息空间为M,且满足:
|M|=|K|=|C|
那么如果方案满足如下两个条件,则可以说明他是完美安全的:
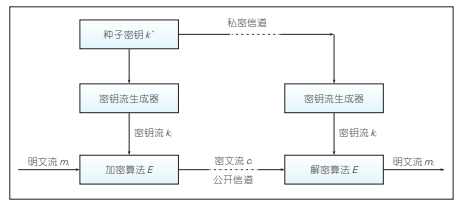
(1)Gen从密钥空间中输出密钥k,如下:
其对应的概率均相等,都为1/|K|
(2)任意选择明文m和密文c,也就是:
都能从密钥空间K中找到对应的密钥k,也就是:
使其满足:
需要将此处的Enc看成加密算法。
完整形式化的定理如下:

证明该定理:
遵循充分必要条件,该定理需要正向证明和反向证明。
(1)理论分析
首先需要根据给定的两个条件,来证明完美安全。首先观察条件2,因为总存在密钥k将对应的明文m和密文c对应,所以密文c和明文m可能存在任意的对应关系。又因为密钥是唯一存在的,且每个密钥的概率均相等,正如一次一密方案,完美安全则很容易被证明。
接着需要根据完美安全,来解释这两个条件成立。完美安全意味着,对任意的明文m和c都至少存在一个密钥使得他们互相对应,再根据:
|M|=|K|=|C|
可以证明对应的密钥只有唯一性存在,那么就很容易说明每个密钥被选取的概率都是相等的,否则完美安全则不成立。
(2)严格的正向证明
不失一般性,可假设加密算法Enc是确定性的。我们首先需要根据条件1和条件2来证明该密码方案是完美安全的。这个证明过程在此专栏的前面有介绍过。
从密文空间C中选取一个密文c,从明文空间M中选取一个明文m,也就是:
令k代表某唯一的密钥,且满足:
![]()
进一步可计算得到:

第一个等号:对应成功的关键在于密钥选择正确
第二个等号:条件1表明
此等式对任意的m和c都是成立的,那么可以直接得出该方案是完美安全的。
(3)严格的反向证明
现在我们已知是完美安全,需要证明条件1和2成立。
选取任意密文:
一定会存在对应的明文m*满足:
![]()
这也就意味着对任意的明文:
其概率均不为0,也就是:
![]()
那么进一步我们将明文写成集合的形式:
![]()
进一步可得:
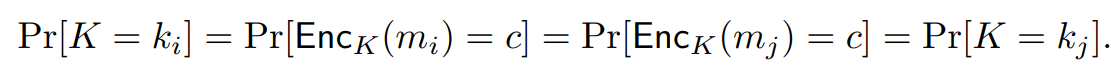
接着很容易证明可得。
六. 小结
在网络安全领域,香农定理可用于证明给定的方案是否为完美安全。
相关文章:

【现代密码学基础】详解完美安全与香农定理
目录 一. 介绍 二. 完美安全的密钥与消息空间 三. 完美安全的密钥长度 四. 最优的完美安全方案 五. 香农定理 (1)理论分析 (2)严格的正向证明 (3)严格的反向证明 六. 小结 一. 介绍 一次一密方案…...

Python 将文本转换成语音播放 pyttsx3
Python 将文本转换成语音播放 pyttsx3 目录 Python 将文本转换成语音播放 pyttsx3 1. 安装 2. 使用 3. 封装 Pyttsx3 是一个 Python 库,它提供了文本到语音(Text-to-Speech,TTS)转换的功能。这个库允许 Python 程序通过调用本…...
FPGA高端项目:Xilinx Artix7系列FPGA 多路视频缩放拼接 工程解决方案 提供4套工程源码+技术支持
目录 1、前言版本更新说明给读者的一封信FPGA就业高端项目培训计划免责声明 2、相关方案推荐我这里已有的FPGA图像缩放方案我已有的FPGA视频拼接叠加融合方案本方案的Xilinx Kintex7系列FPGA上的ov5640版本本方案的Xilinx Kintex7系列FPGA上的HDMI版本 3、设计思路框架设计框图…...

开源模型应用落地-业务优化篇(三)
一、前言 假如您跟随我的脚步,学习到上一篇的内容,到这里,相信细心的您,已经发现了,在上一篇中遗留的问题。那就是IM服务过载的时候,如何进行水平扩容? 因为在每个IM服务中,我们用JV…...

基于SpringBoot+Vue实现的物流快递仓库管理系统
基于SpringBootVue实现的物流快递仓库管理系统 文章目录 基于SpringBootVue实现的物流快递仓库管理系统系统介绍技术选型成果展示账号地址及其他说明源码获取 系统介绍 系统演示 关注视频号【全栈小白】,观看演示视频 基于SpringBootVue实现的物流快递仓库管理系…...

编程笔记 html5cssjs 072 JavaScrip BigInt数据类型
编程笔记 html5&css&js 072 JavaScrip BigInt数据类型 一、BigInt 数据类型二、BigInt 的创建和使用三、BigInt 操作与方法三、示例小结 JavaScript BigInt 数据类型是一种内置的数据类型,用于表示大于 Number.MAX_SAFE_INTEGER(即2^53 - 1&…...

matlab simulink 步进电机控制
1、内容简介 略 41-可以交流、咨询、答疑 2、内容说明 电动执行器定位控制在生产生活中具有广泛的应用,在使用搭载步进电机的电动执行器进行定位控制的时候,定位系统的定位精度和响应波形,会随着负载质量的变化而变化,这是由电…...
使用阿里云的IDaaS实现知行之桥EDI系统的单点登录
,在开始测试之前,需要确定用哪个信息作为“登陆用户的ID字段”。 这个字段用来在完成SSO登陆之后,用哪个信息将阿里云IDaaS的用户和知行之桥EDI系统的用户做对应。这里我们使用了 phonenumber 这个自定义属性。需要在阿里云做如下配置&#x…...
基于微服务的高考志愿智能辅助决策系统(附源码)
目录 一.引言 1、编写目的 2、系统功能概述 二.功能分析 三.微服务模块 1、微服务用户相关模块 (1)用户注册 (2)用户登录 (3)用户信息管理 (4)用户操作 2、微服务文件云存…...

LeetCode —— 137. 只出现一次的数字 II
😶🌫️😶🌫️😶🌫️😶🌫️Take your time ! 😶🌫️😶🌫️😶🌫️😶🌫️…...

pnpm、npm、yarn 包管理工具
1、npm 关键词:软件包管理器、命令行工具、一个社区和一个平台 npm(Node Package Manager)是一个用于Node.js环境的软件包管理器。它是一个命令行工具,用于安装、升级、删除和管理JavaScript软件包。npm最初是随同Node.js一起发布…...

微服务知识
1、概念 大型单体应用拆分成多个独立部署运行的微服务(解决并发问题) 2、特点 3、技术栈 4、微服务带来的问题 5、微服务的注册中心 服务注册与发现:微服务实例在启动时会向注册中心注册自己的信息…...

如何在微信搭建私域流量池?
A: ①给客户打标签 添加标签,多维度构建用户画像,精准发送消息。 ②群发信息 选择自定义时间,上传内容 (支持文字,图片) ,一键群发 。 ③建立专属素材库 将常用的话术、图片与文件录入至素材库,员工可随…...

MySQL原理(三)锁定机制(1)综述
一、介绍: 1、锁的本质 业务场景中存在共享资源,多个进程或线程需要竞争获取并处理共享资源,为了保证公平、可靠、结果正确等业务逻辑,要把并发执行的问题变为串行,串行时引入第三方锁当成谁有权限来操作共享资源的判…...

Qt知识点总结
将枚举类型转换为字符串 这里使用的在网络编程中,获取socket状态并显示的时候,遇到的一个问题 #include <QMetaEnum>// 将枚举类型转换为字符串 QMetaEnum metaEnum QMetaEnum::fromType<QAbstractSocket::SocketState>(); const char *c…...
13)
什么是系统工程(字幕)13
0 00:00:00,670 --> 00:00:01,582 如果不加图 1 00:00:01,582 --> 00:00:02,130 怎么加 2 00:00:02,130 --> 00:00:03,225 我们来看一下 3 00:00:03,225 --> 00:00:03,590 你看 4 00:00:03,980 --> 00:00:06,720 右键点这个,添加元素 5 00:00:0…...
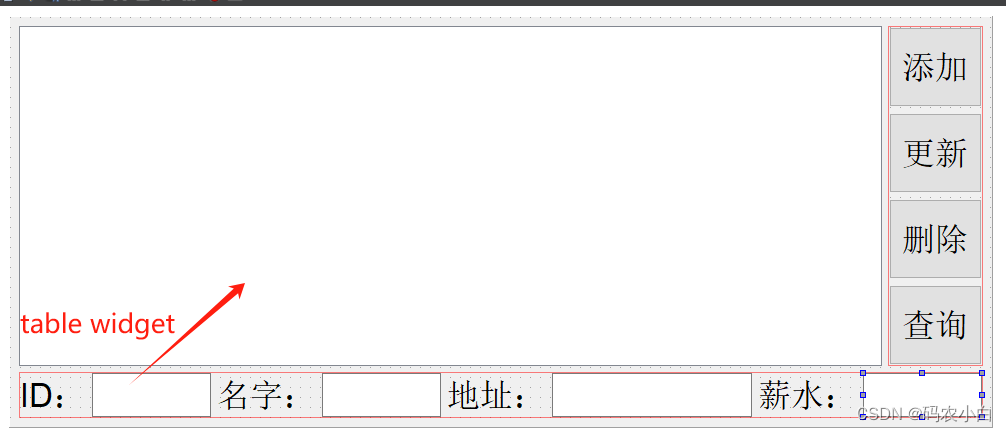
qt学习:Table widget控件
目录 头文件 实战 重新配置ui界面 添加头文件 在构造函数中添加初始化 显示方法 该实例是在sqlite项目上添加qt学习:QTSQL连接sqlite数据库增删改查-CSDN博客 头文件 #include <QTableWidgetItem> 实战 重新配置ui界面 用法介绍,可以双击…...

Android --- Content Provider是使用示例,通俗易懂
当两个应用程序之间需要共享数据时,可以通过 Content Provider 来实现。在这个示例中,我们将创建一个简单的 Content Provider,让 App_B 暴露人口总数的数据,并由 App_A 来获取这个数据。 首先,我们来创建一个简单的示…...

02-opencv简单实例效果和基本介绍-上
机器视觉概述 机器视觉是人工智能正在快速发展的一个分支。简单说来,机器视觉就是用机器代替人眼来做测量和判断。机器视觉系统是通过机器视觉产品(即图像摄取装置,分CMOS和CCD两种)将被摄取目标转换成图像信号,传送给专用的图像处理系统,得到被摄目标的形态信息,根据像素…...
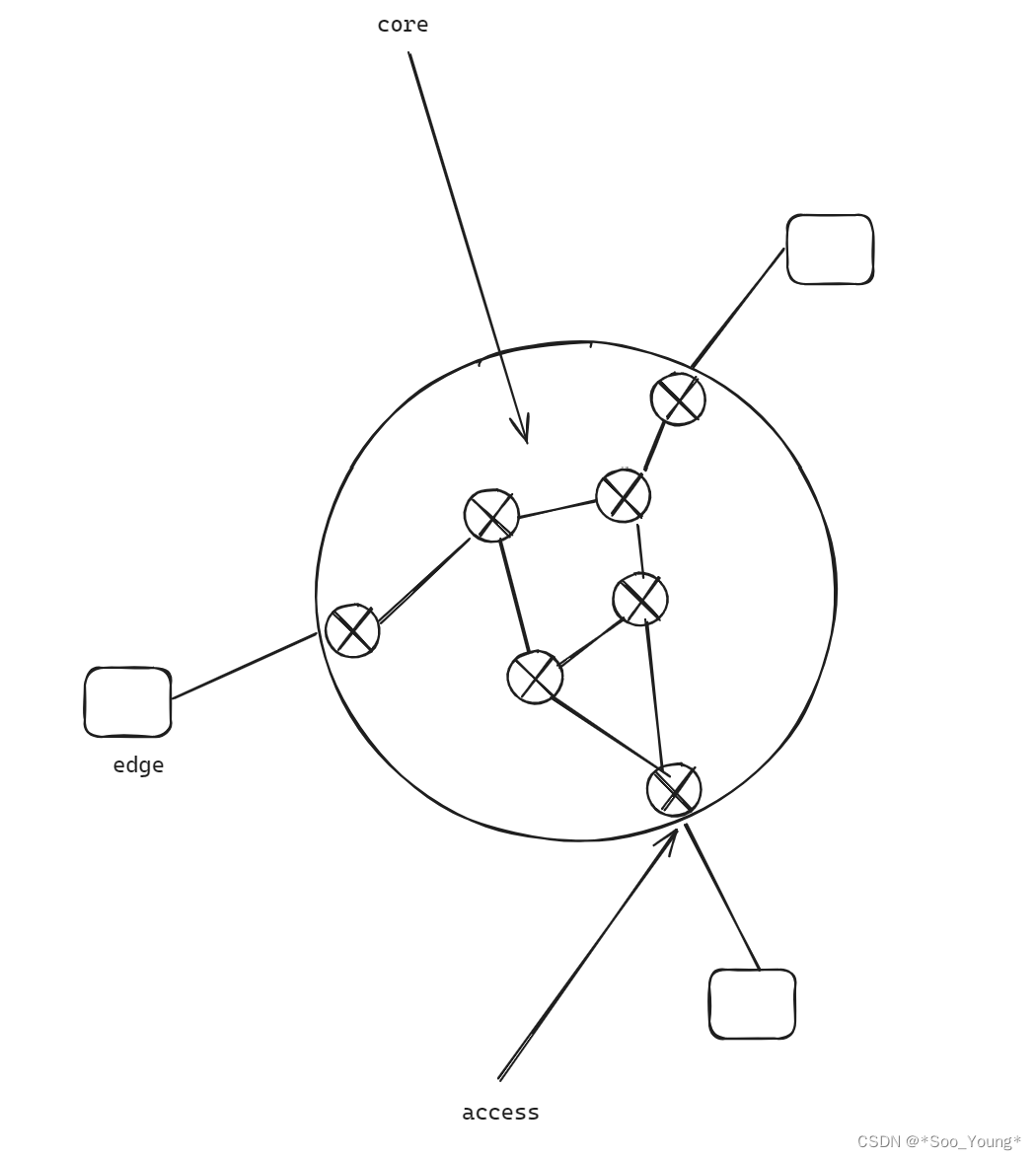
中科大计网学习记录笔记(一):Internet | 网络边缘
计算机网络 前言: 学习视频:中科大郑烇、杨坚全套《计算机网络(自顶向下方法 第7版,James F.Kurose,Keith W.Ross)》课程 该视频是B站非常著名的计网学习视频,但相信很多朋友和我一样在听完前面…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
